геометрия_6_уравнение-плоскости-и-прямой_теория-У

1.

Уравнение прямой,
плоскости и сферы
в пространстве
11 класс
06.01.2026

2.

06.01.2026

3.

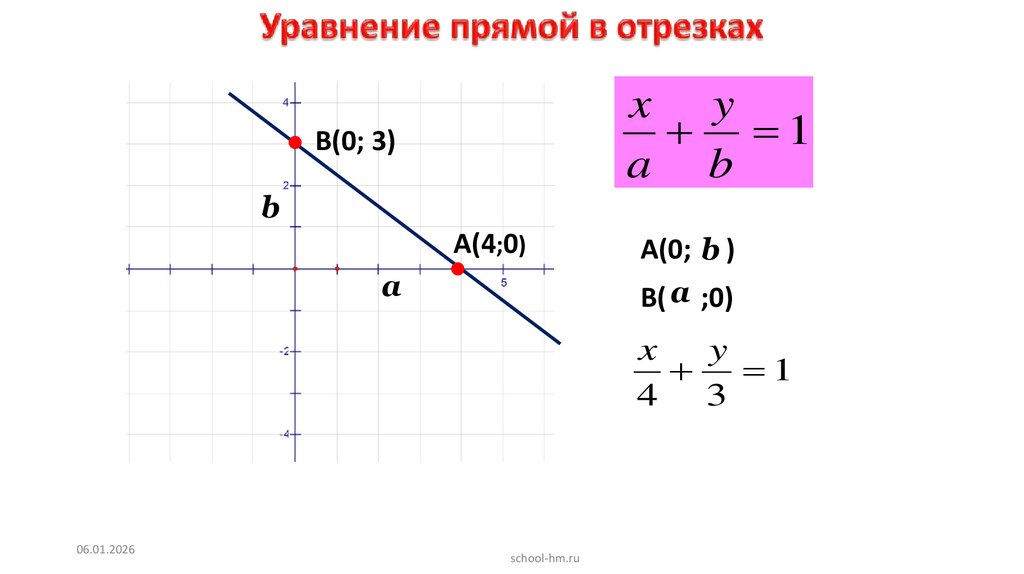
x y
1
a b
В(0; 3)
b
А(4;0)
а
А(0; b )
В( a ;0)
x
y
1
4 3
06.01.2026
school-hm.ru

4.

x y
1
a b
b
x
y
1
1
3
а
x
y
1
3 4
x
y
1
5
2
06.01.2026
school-hm.ru

5.

06.01.2026

6.

06.01.2026

7.

y
b
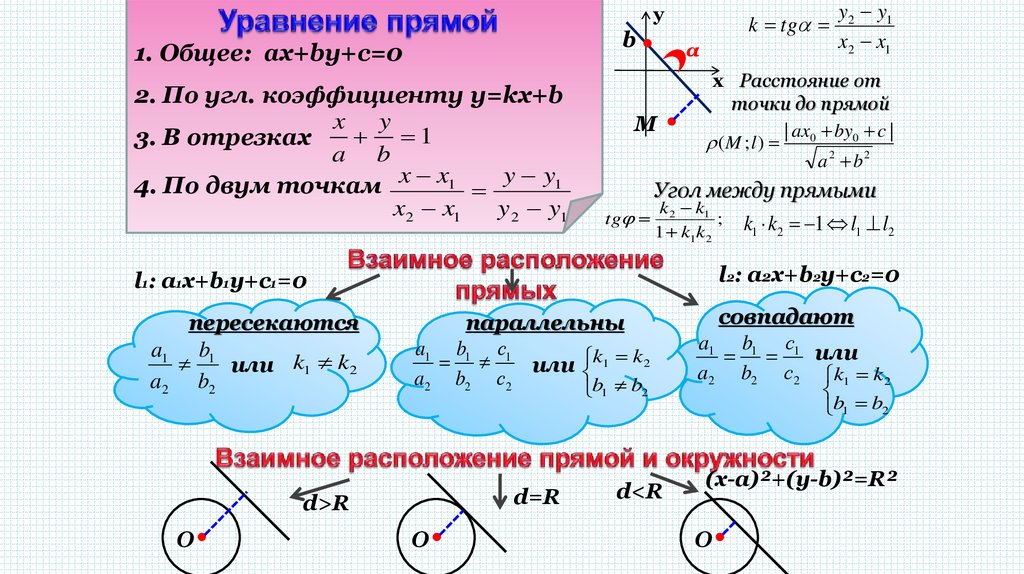
1. Общее: ax+by+c=0
2. По угл. коэффициенту y=kx+b
x y
1
3. В отрезках
a b
4. По двум точкам x x1 y y1
x2 x1
y 2 y1
k tg
α
M
x Расстояние от
точки до прямой
| ax0 by0 c |
(M ; l )
a 2 b2
Угол между прямыми
tg
k 2 k1
;
1 k1k 2
параллельны
a1 b1 с1
k1 k 2
или
a2 b2 с2
b b
1
d=R
d>R
O
k1 k2 1 l1 l2
l2: a2x+b2y+c2=0
l1: a1x+b1y+c1=0
пересекаются
a1 b1
или k1 k2
a2 b2
y2 y1
x2 x1
O
совпадают
a1 b1 с1
или
a2 b2 с2 k1 k 2
b1 b2
2
d<R
(x-a)²+(y-b)²=R²
O

8.

06.01.2026

9.

Уравнение плоскости, проходящей через данную
точку перпендикулярно данному вектору
n{ А; В; С}
А( x0 ; у0 ; z0 )
В ( x; y; z )
А( x0 ; у0 ; z0 )
n
n{ A; B; C} -нормальный
вектор плоскости
В( x; y; z )
АB x x0 ; y y0 ; z z0
n АB 0
А( x x0 ) В( y y 0 ) С ( z z0 ) 0
Аx Вy Сz D 0
06.01.2026
, где
D ( Ax0 By 0 Cz0 )

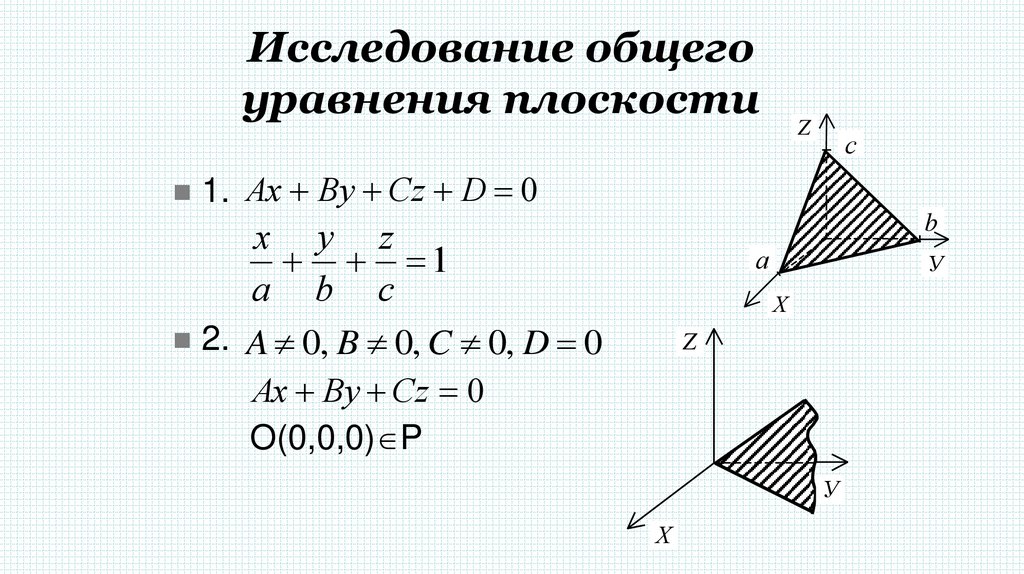
10. Исследование общего уравнения плоскости

Z
с
1. Ax By Cz D 0
b
x y z
1
a b c
2. A 0, B 0, C 0, D 0
а
У
Х
Z
Ax By Cz 0
O(0,0,0) P
У
Х

11.

06.01.2026

12.

06.01.2026

13.

06.01.2026

14.

06.01.2026

15.

6. Составить уравнение плоскости, проходящей через точки А(-2;3;5),
В(4;-3;0), С(0;6;-5) и найти координаты вектора нормали.
06.01.2026

16.

06.01.2026

17.

Угол между плоскостями
: a1x b1 y c1z d1 0
Вектор нормали плоскости : n1{a1 ; b1 ; c1}
: a2 x b2 y c2 z d2 0
Вектор нормали плоскости : n2 {a2 ; b2 ; c2 }
cos
06.01.2026
| a1 a2 b1 b2 c1 c2 |
a1 b1 c1 a2 b2 c2
2
2
2
2
2
2

18.

06.01.2026

19.

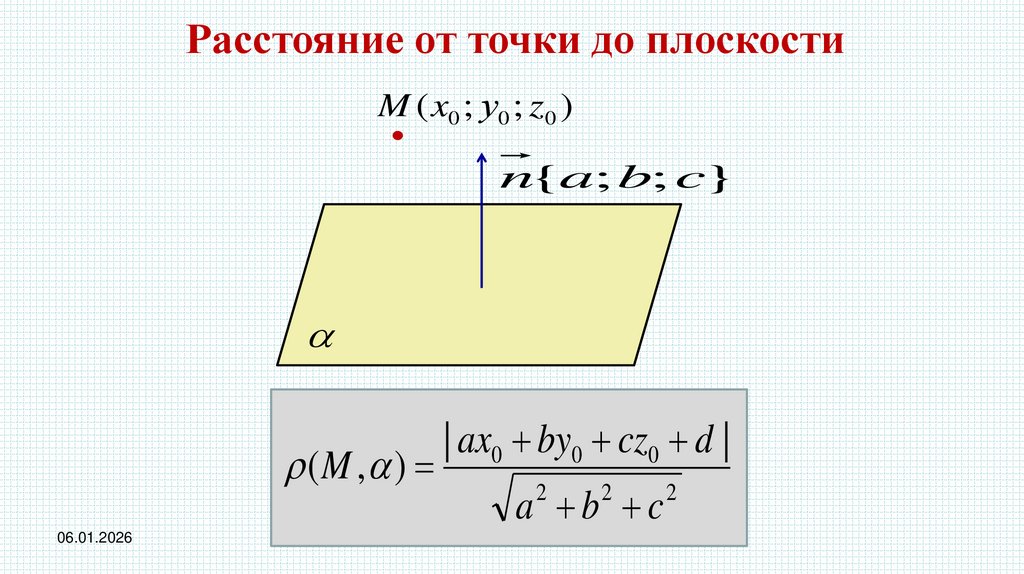
Расстояние от точки до плоскости
M ( x0 ; у0 ; z0 )
n{a; b; c}
(M , )
06.01.2026
| ax0 by0 cz0 d |
a b c
2
2
2

20.

8.
06.01.2026

21.

Прямая на плоскости
Прямая в пространстве
M 0 ( x0 , y 0 )
l (m, n)
M 0 ( x0 , y 0 , z 0 )
l (m, n, p )
x x 0 tm
y y 0 tn
x x 0 tm
y y 0 tn
z z tp
0
24

22.

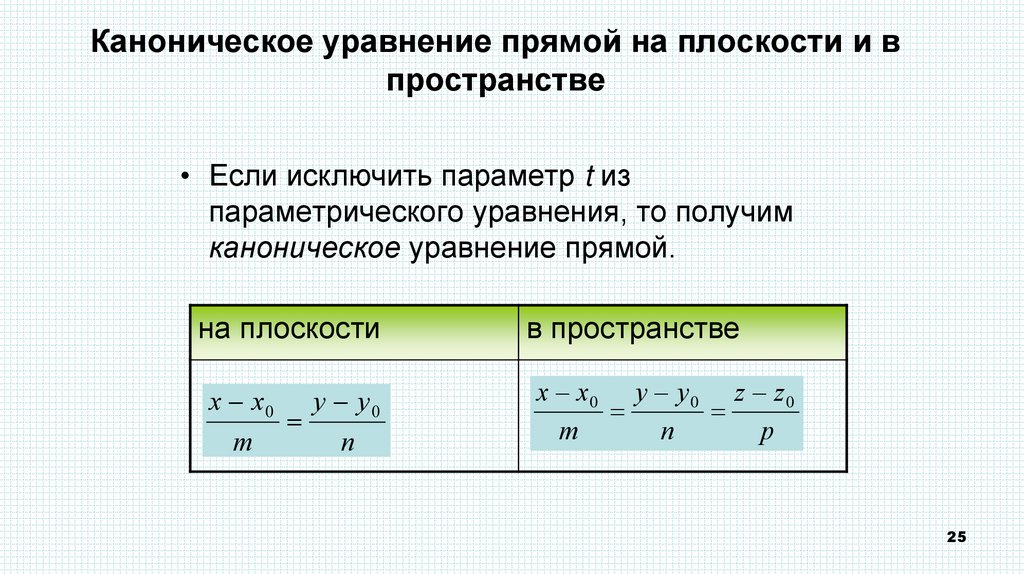
Каноническое уравнение прямой на плоскости и в
пространстве
• Если исключить параметр t из
параметрического уравнения, то получим
каноническое уравнение прямой.
на плоскости
в пространстве
x x0 y y 0
m
n
x x0 y y 0 z z 0
m
n
p
25

23.

Уравнение прямой проходящей через две
точки М1 и М2
на плоскости
в пространстве
M 1 ( x1 , y1 ), M 2 ( x 2 , y 2 ) M 1 ( x1 , y1 , z1 ), M 2 ( x 2 , y 2 , z 2 )
M ( x, y, z )
M ( x, y)
l M 1M 2
M 1 M 2 ( x 2 x1 , y 2 y1 ) M 1 M 2 ( x 2 x1 , y 2 y1 , z 2 z1 )
x x1
y y1
x 2 x1 y 2 y1
x x1
y y1
z z1
x 2 x 1 y 2 y1 z 2 z 1
26

24.

06.01.2026

25. Каноническое уравнение прямой на плоскости и в пространстве

06.01.2026

26. Уравнение прямой проходящей через две точки М1 и М2

06.01.2026

27.

06.01.2026

28.

06.01.2026

29.

06.01.2026

30.

На плоскости
Общее ур-ние прямой
Ур-ние прямой в отрезках
В пространстве
Общее ур-ние плоскости
а(