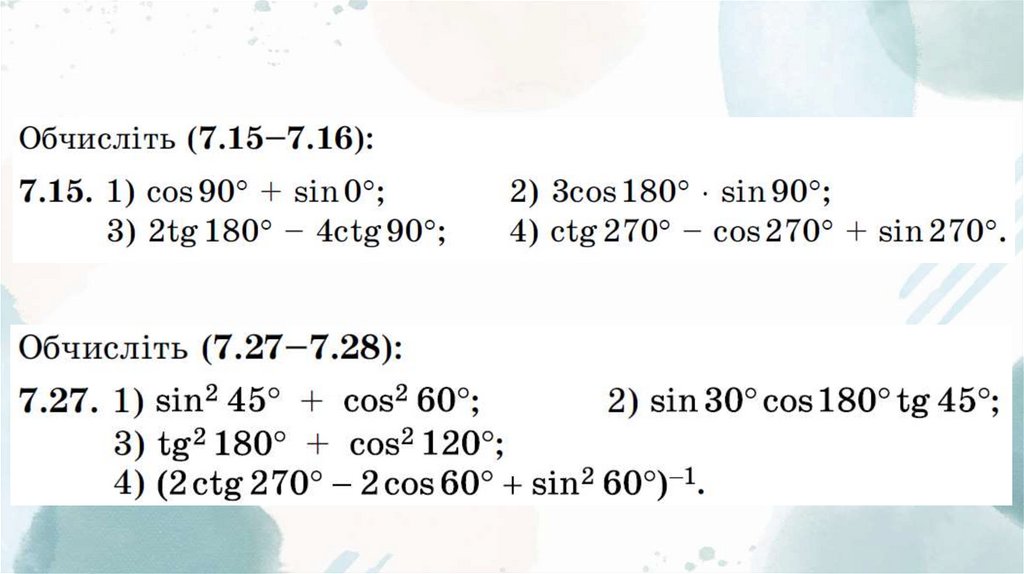15. Синус косинус

1. Синус, косинус, тангенс, котангенс кута

15
06.01.2026

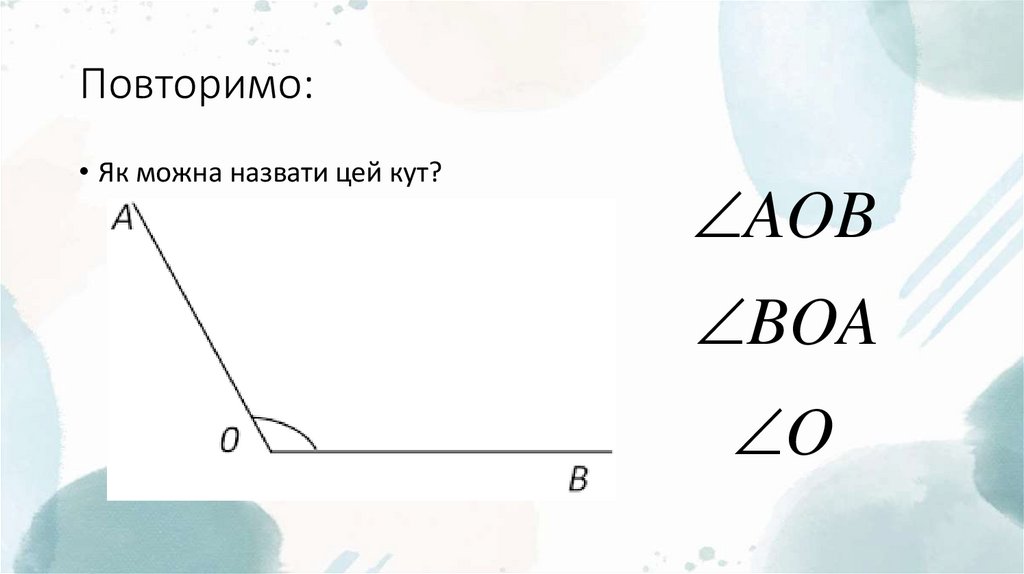
2. Повторимо:

• Як можна назвати цей кут?
AOB
BOA
O

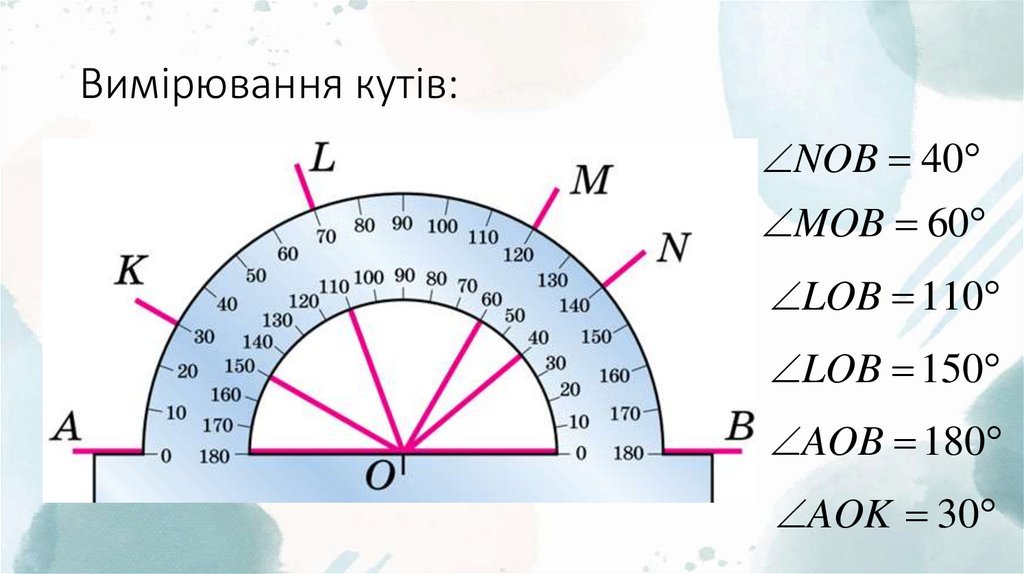
3. Вимірювання кутів:

NOB 40
MOB 60
LOB 110
LOB 150
AOB 180
AOK 30

4. Класифікація за величиною:

•Гострий (від 0° до 90°)
•Прямий (90°)
•Тупий (від 90° до 180°)
•Розгорнутий (180°)

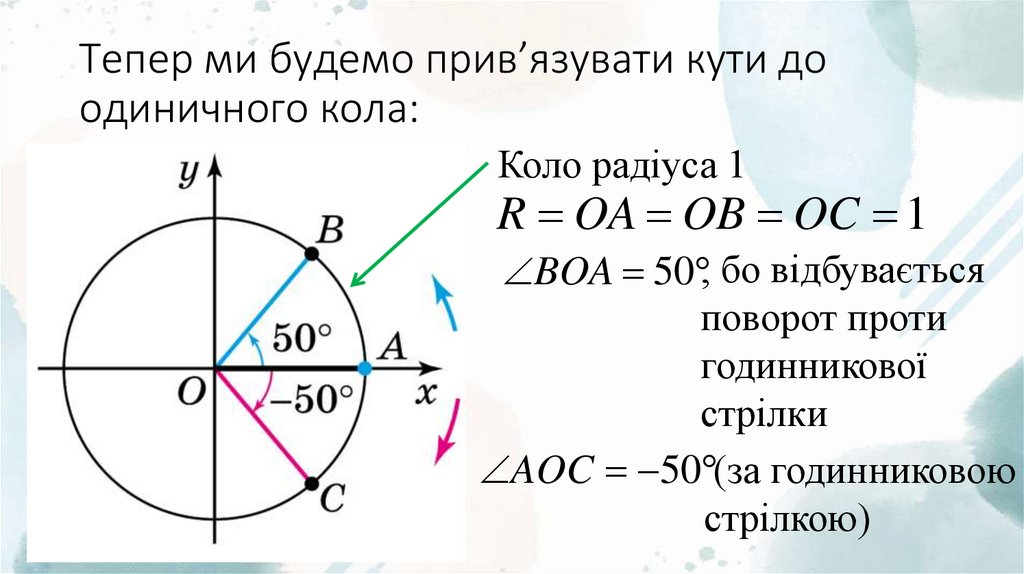
5. Тепер ми будемо прив’язувати кути до одиничного кола:

Коло радіуса 1
R OA OB OC 1
BOA 50 , бо відбувається
поворот проти
годинникової
стрілки
AOC 50 (за годинниковою
стрілкою)

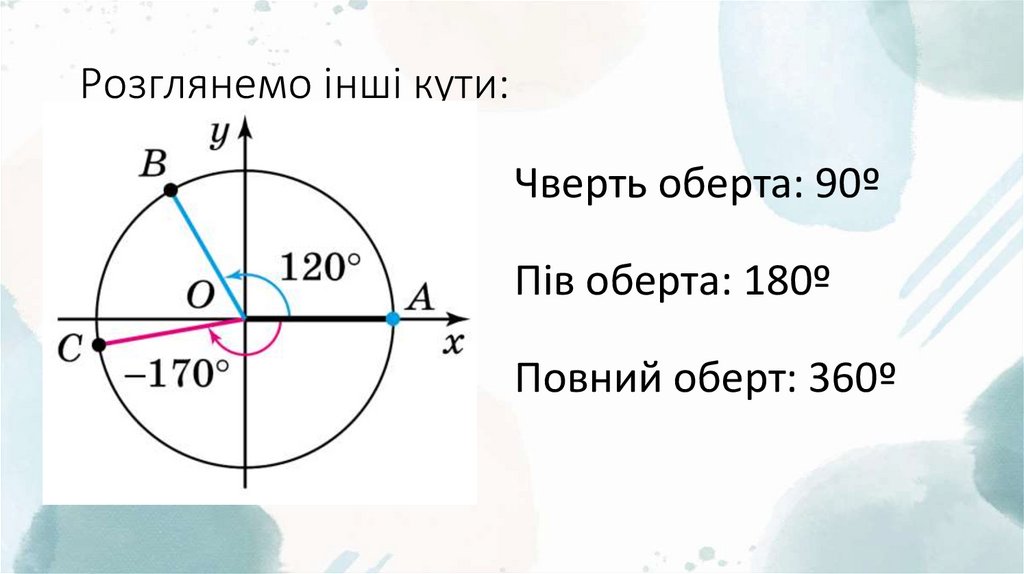
6. Розглянемо інші кути:

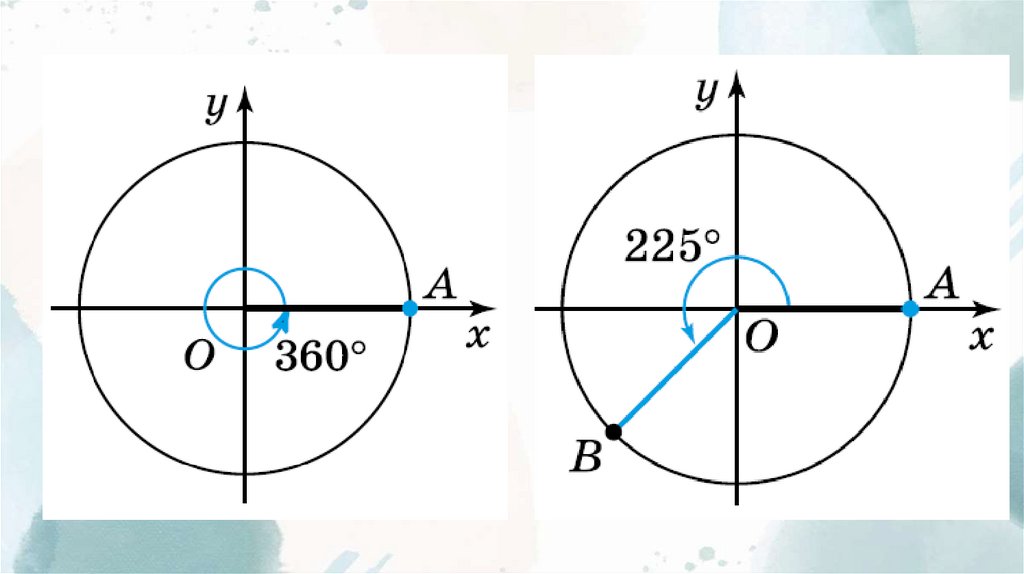
Чверть оберта: 90º
Пів оберта: 180º
Повний оберт: 360º

7.

8.

9.

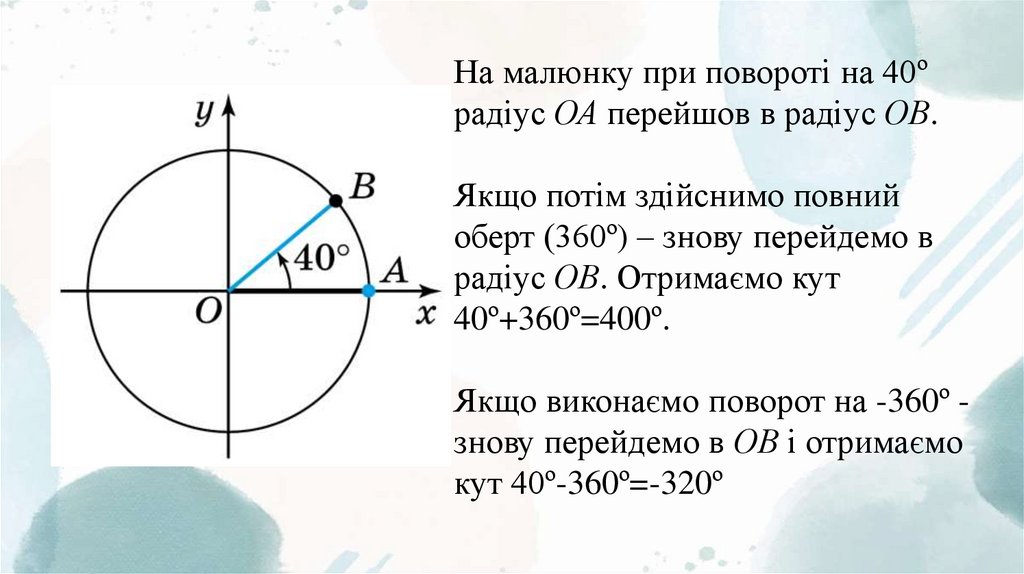
На малюнку при повороті на 40º
радіус ОА перейшов в радіус ОВ.
Якщо потім здійснимо повний
оберт (360º) – знову перейдемо в
радіус ОВ. Отримаємо кут
40º+360º=400º.
Якщо виконаємо поворот на -360º знову перейдемо в ОВ і отримаємо
кут 40º-360º=-320º

10. Будь-який кут можна подати у вигляді

•Наприклад,

11. Належність кутів чвертям:

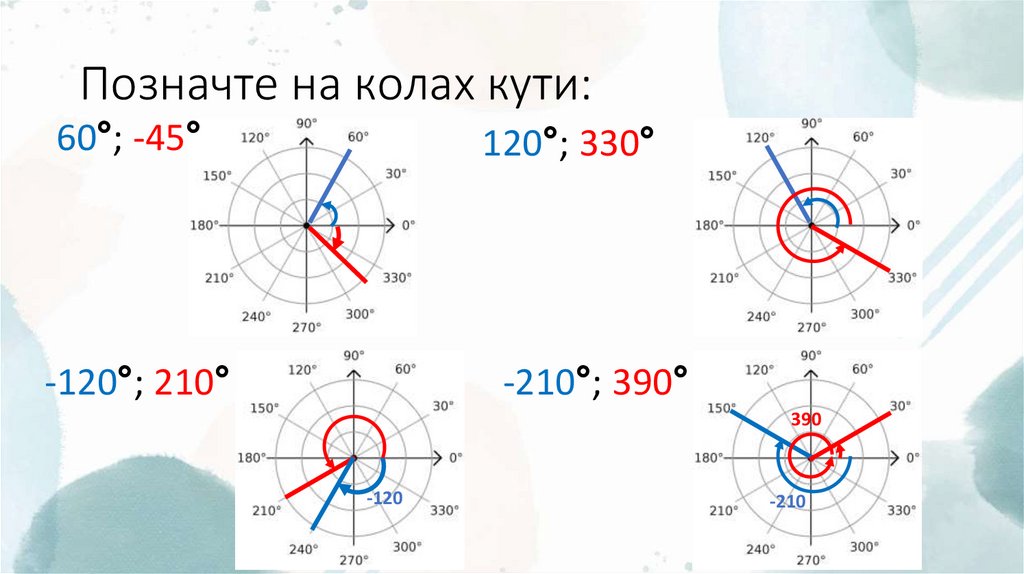
12. Позначте на колах кути:

60°; -45°
120°; 330°
-120°; 210°
-210°; 390°
390
-120
-210

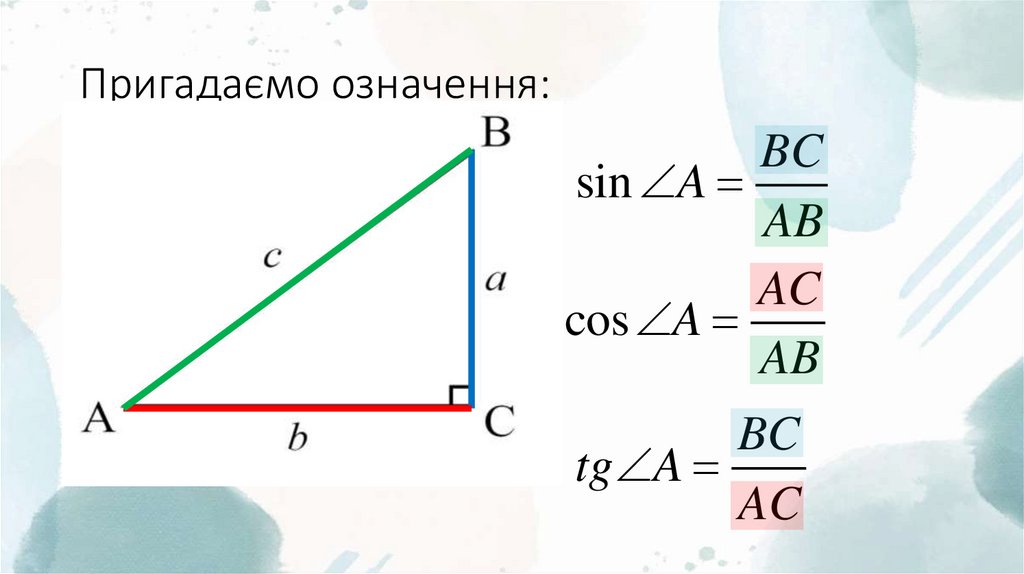
13. Пригадаємо означення:

BC
sin A
AB
AC
cos A
AB
BC
tg A
AC

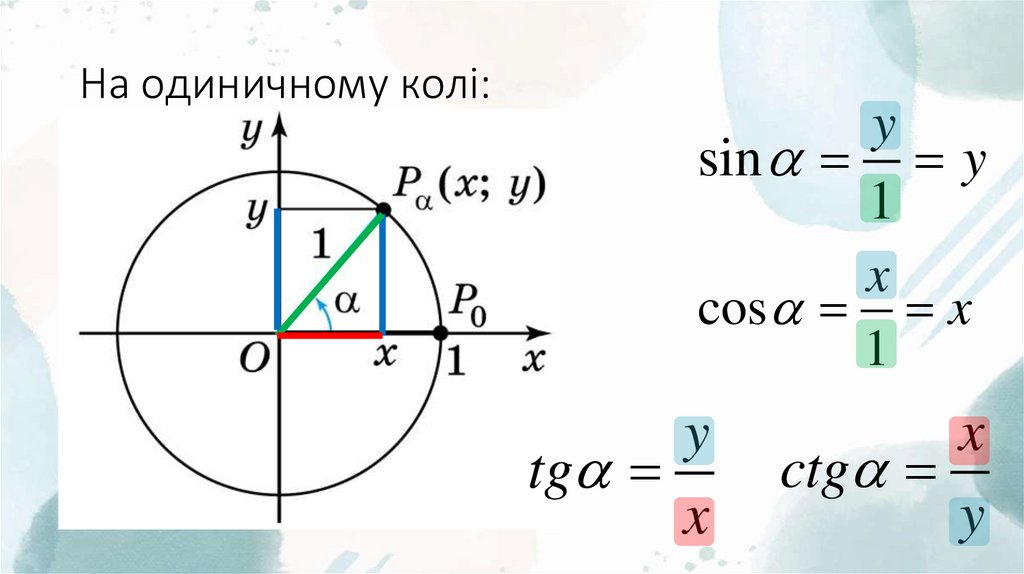
14. На одиничному колі:

y
sin y
1
x
cos x
1
y
tg
x
x
ctg
y

15.

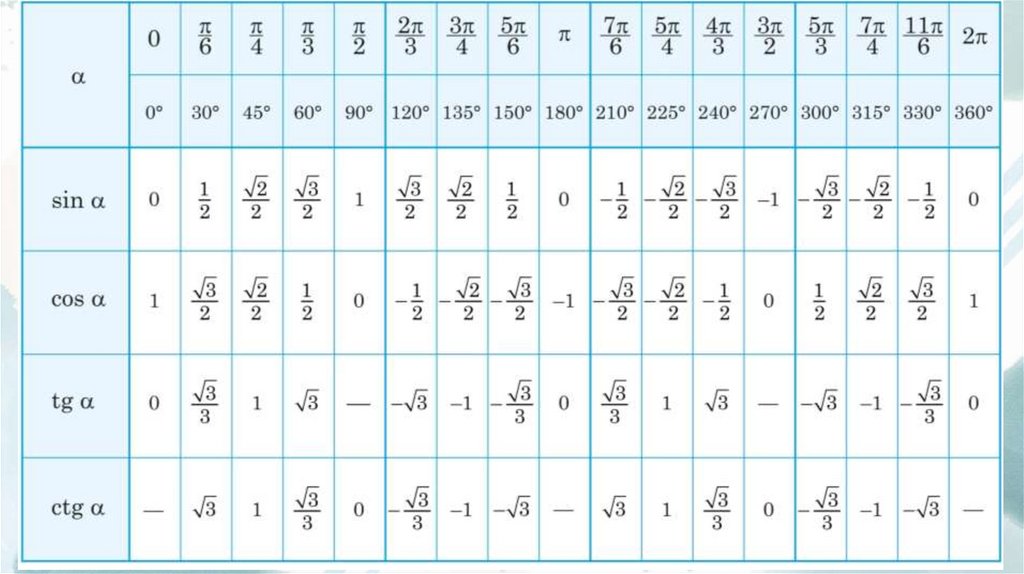
16. Тригонометричні значення деяких кутів

17.

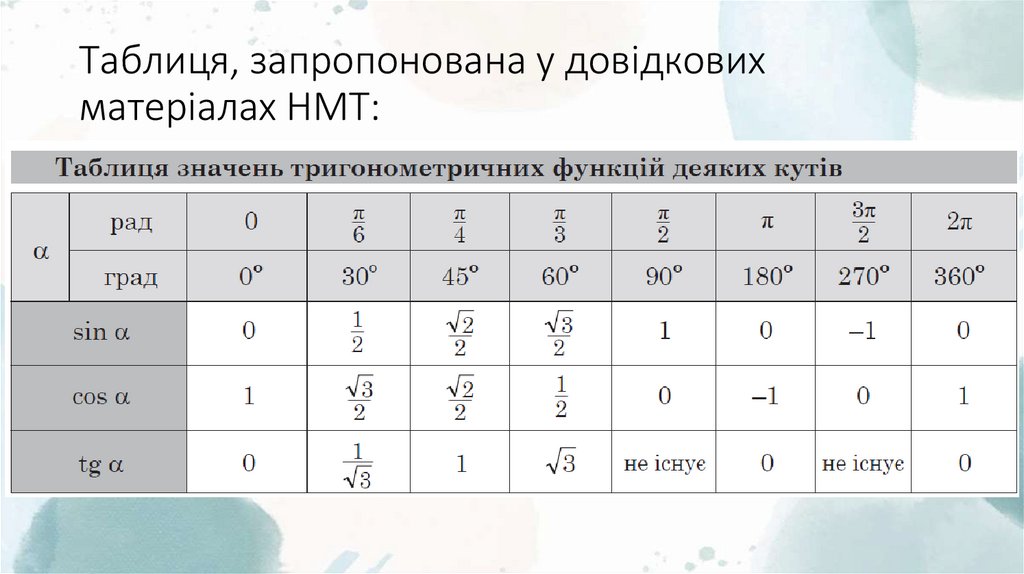
18. Таблиця, запропонована у довідкових матеріалах НМТ:

19. Вправи:

20.

21.

22. Підсумки:

• Правильним чи неправильним є твердження:
1) Синусом кута є абсциса відповідної куту точки
на одиничному колі;
2) Тангенс 90° не існує;
3) Від’ємний
кут
відраховуємо
на
тригонометричному колі у напрямку проти
годинникової стрілки;
4) Котангенс кута – це відношення косинуса
до синуса цього кута;

23. Домашнє завдання:

• Параграф 7 (ст. 68-74)
• Вправи 7.8, 7.10, 7.16

24. Використана література:

1. Істер О.С. Математика :
(алгебра і початки аналізу та
геометрія, рівень стандарту) :
підруч. для 10-го кл. закл. заг.
серед. освіти— Київ : Генеза,
2018. — 384 с. : іл.