Лекция_12_формулы_19.11.2024

1. Лекция №12 Разработка программного обеспечения для моделирования физических процессов

Санкт-Петербургский политехнический университет Петра Великого
Лекция №12
Разработка программного обеспечения
для моделирования физических
процессов
Воскобойников С.П.
Доцент ВШ ПИ ИКНТ, к.ф.-м.н.
voskob_sp@spbstu.ru
19.11.2024

2. Содержание

Задача с граничными условиями первого рода
Переход от двухиндексной записи уравнений к
одноиндексной. Приведённый индекс.
Структура системы линейных алгебраических
уравнений.
Понижение размерности за счёт исключения
известных значений.
Задача с граничными условиями первого и третьего
рода
Структура системы линейных алгебраических
уравнений.
Метод Гаусса для ленточных систем. Схема
хранения в симметричном и несимметричном
случае.
Метод матричной прогонки.

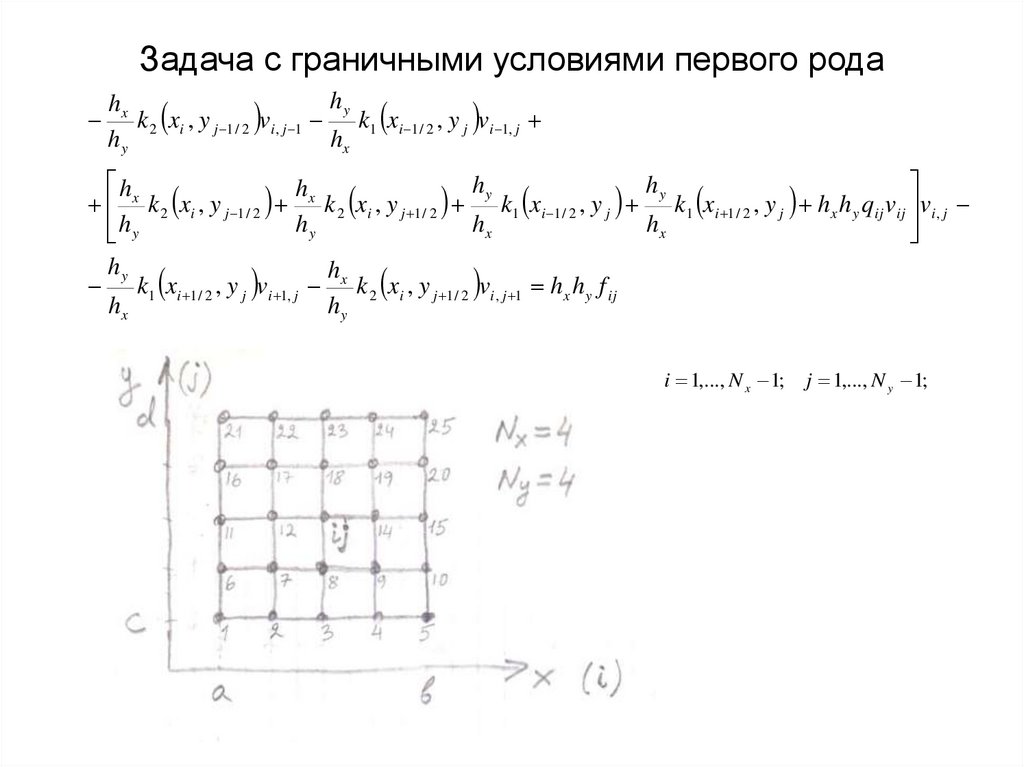
3. Задача с граничными условиями первого рода

u
u
k1 x, y k2 x, y q x, y u f x, y
x y
y
x
Краевые условия первого рода
u x a 1 ,
u x b 2
Краевые условия первого рода
u y c 3 ,
u y d 4
N x число разбиений интервала a, b
x0 x1 ... xN x ,
xi a, b ,
x0 a, xN x b
hi xi xi 1 , i 1,2,..., N x
xi 1 / 2
xi xi 1
,
2
i 1,2,..., N x
hi 1
i 0
2 ,
h h
i i i 1 , i 1,2,..., N x 1
2
hi
i Nx
2 ,
N y число разбиений интервала c, d
y0 y1 ... yN y , y j c, d , y0 c, yN y d
h j y j y j 1 , j 1,2,..., N y
y j 1 / 2
y j y j 1
2
,
j 1,2,..., N y
h j 1
j 0
2 ,
h h j 1
j j
, j 1,2,..., N y 1
2
hj
j Ny
2,

4. Задача с граничными условиями первого рода

vi 1, j vi , j
vi , j vi 1, j
j k1 xi 1 / 2 , y j
j k1 xi 1 / 2 , y j
h
h
i 1
i
i k2 xi , y j 1 / 2
vi , j 1 vi , j
h j 1
i k2 xi , y j 1 / 2
j 0,1,..., N y
j 0,
vi , j 1 y j , i 0,
vi , j 3 x i , i 0,1,..., N x ,
vi , j vi , j 1
hj
i j qijvij i j fij
vi , j 2 y j , i N x ,
j 0,1,..., N y
vi , j 4 x i , i 0,1,..., N x ,
j Ny,
N N x 1 N y 1
xi a ihx ,
i 0,1,..., N x
hi hx
b a
,
Nx
y j c jhy ,
j 0,1,..., N y
h j hy
v v
v v
hy k1 xi 1/ 2 , y j i 1, j i , j hy k1 xi 1/ 2 , y j i , j i 1, j
hx
hx
v v
v v
hx k 2 xi , y j 1/ 2 i , j 1 i , j hx k 2 xi , y j 1/ 2 i , j i , j 1 hx hy qij vij hx hy f ij
hy
hy
d c
,
Ny

5. Задача с граничными условиями первого рода

hy
hx
k 2 xi , y j 1 / 2 vi , j 1 k1 xi 1 / 2 , y j vi 1, j
hy
hx
hx
hy
hy
hx
k 2 xi , y j 1 / 2 k 2 xi , y j 1 / 2 k1 xi 1 / 2 , y j k1 xi 1 / 2 , y j hx h y qij vij vi , j
hy
hx
hx
h y
hy
h
k1 xi 1 / 2 , y j vi 1, j x k 2 xi , y j 1 / 2 vi , j 1 hx h y f ij
hx
hy
i 1,..., N x 1;
j 1,..., N y 1;

6. Переход к одному индексу. Приведённый индекс.

i 0,1,..., N x ;
j 0,1,..., N y ;
i, j m Lj i 1,
j 0,1,..., N y ;
L N x 1
i 0,1,..., N x ;
m jL i 1,
L N x 1
vi , j 1 wm L
vi 1, j wm 1
vi , j wm
vi 1, j wm 1
vi , j 1 wm L
j 1,..., N y 1;
i 1,..., N x 1;
m jL i 1,
am wm L bm wm 1 cm wm d m wm 1 em wm L g m ,

7. ИИМ для уравнений эллиптического типа

am
cm
hx
k 2 xi , y j 1/ 2 ,
hy
bm
hy
hx
k1 xi 1 / 2 , y j
h
h
hx
h
k 2 xi , y j 1/ 2 x k 2 xi , y j 1/ 2 y k1 xi 1/ 2 , y j y k1 xi 1/ 2 , y j hx hy qij
hy
hy
hx
hx
dm
hy
hx
em
hx
k 2 xi , y j 1/ 2
hy
cm wm g m ,
cm 1,
g m 1 y j
k1 xi 1 / 2 , y j
g m hx hy f ij
m jL i 1,
i 0;
j 1,..., N y 1;
i Nx;
j 1,..., N y 1;
cm wm g m ,
cm 1,
g m 2 y j
i 0,1,..., N x ; j 0;
cm wm g m ,
cm 1,
g m 3 xi
i 0,1,..., N x ;
cm wm g m ,
cm 1,
g m 4 xi
j Ny
Aw g
A R N N ,
w, g R N , N ( N x 1)( N y 1)

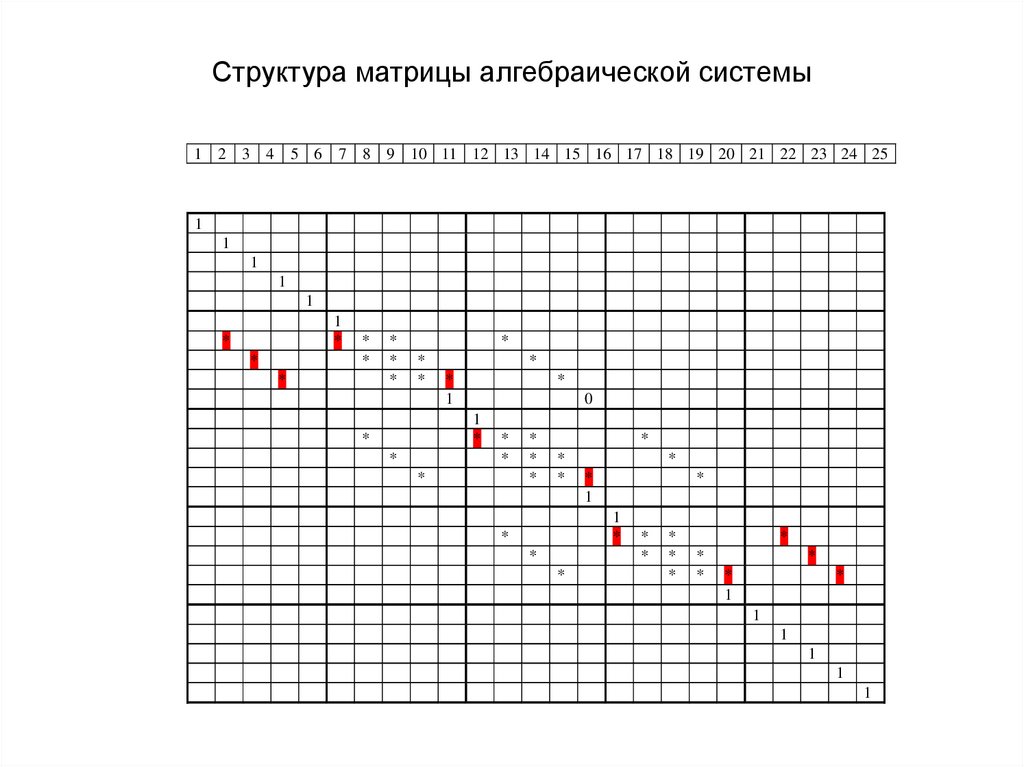
8. Структура матрицы алгебраической системы

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
1
1
1
1
1
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
1
*
0
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
1
*
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
1
*
1
1
1
1
1

9. Симметризация исключением неизвестных

1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
1
1
1
1
1
1
*
*
*
*
*
*
*
*
*
*
1
0
1
*
*
*
*
*
*
*
*
*
*
*
*
*
1
1
*
*
*
*
*
*
*
*
*
*
1
1
1
1
1
1

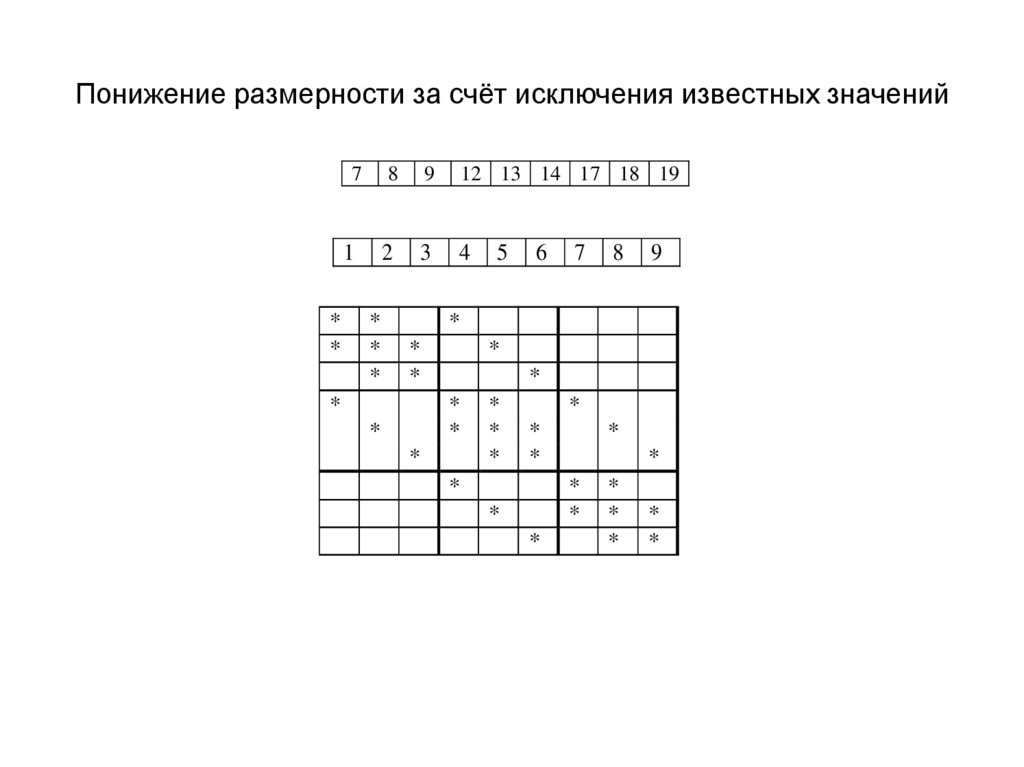
10. Понижение размерности за счёт исключения известных значений

m jL i,
j 2,..., N y 2;
L N x 1
i 2,..., N x 2;
h
hx
k 2 xi , y j 1/ 2 vi , j 1 y k1 xi 1/ 2 , y j vi 1, j
hy
hx
hx
hy
hy
hx
k 2 xi , y j 1/ 2 k 2 xi , y j 1/ 2 k1 xi 1/ 2 , y j k1 xi 1/ 2 , y j hx hy qij vi , j
hy
hx
hx
hy
hy
h
k1 xi 1/ 2 , y j vi 1, j x k 2 xi , y j 1/ 2 vi , j 1 hx hy f ij
hx
hy
am wm L bm wm 1 cm wm d m wm 1 em wm L g m ,

11. Понижение размерности за счёт исключения известных значений

j 1;
hy
hx
i 2,..., N x 2;
k1 xi 1/ 2 , y j vi 1, j
h
h
h
h
x k 2 xi , y j 1/ 2 x k 2 xi , y j 1/ 2 y k1 xi 1/ 2 , y j y k1 xi 1/ 2 , y j hx hy qij vi , j
hy
hx
hx
hy
h
h
h
y k1 xi 1/ 2 , y j vi 1, j x k 2 xi , y j 1/ 2 vi , j 1 hx hy f ij x k 2 xi , y j 1/ 2 3 xi
hx
hy
hy
bm wm 1 cm wm d m wm 1 em wm L g m ,
gm hx hy fij
hx
k2 xi , y j 1 / 2 3 xi .
hy

12. Понижение размерности за счёт исключения известных значений

j N y 1;
i 2,..., N x 2;
h
hx
k 2 xi , y j 1/ 2 vi , j 1 y k1 xi 1/ 2 , y j vi 1, j
hy
hx
hx
hy
hy
hx
k 2 xi , y j 1/ 2 k 2 xi , y j 1/ 2 k1 xi 1/ 2 , y j k1 xi 1/ 2 , y j hx hy qij vi , j
hy
hx
hx
hy
h
h
y k1 xi 1/ 2 , y j vi 1, j hx hy f ij x k 2 xi , y j 1/ 2 4 xi
hx
hy
am wm L bm wm 1 cm wm dm wm 1 gm ,
gm hx hy fij
hx
k2 xi , y j 1 / 2 4 xi
hy

13. Понижение размерности за счёт исключения известных значений

i 1;
j 2,..., N y 2;
hx
k 2 xi , y j 1/ 2 vi , j 1
hy
h
h
h
h
x k 2 xi , y j 1/ 2 x k 2 xi , y j 1/ 2 y k1 xi 1/ 2 , y j y k1 xi 1/ 2 , y j hx hy qij vi , j
hy
hx
hx
hy
h
h
h
y k1 xi 1/ 2 , y j vi 1, j x k 2 xi , y j 1/ 2 vi , j 1 hx hy f ij y k1 xi 1/ 2 , y j v1 y j
hx
hy
hx
am wm L cm wm dm wm 1 em wm L gm ,
gm hx hy fij
hy
hx
k1 xi 1 / 2 , y j v1 y j

14. Понижение размерности за счёт исключения известных значений

i N x 1;
j 2,..., N y 2;
h
hx
k 2 xi , y j 1/ 2 vi , j 1 y k1 xi 1/ 2 , y j vi 1, j
hy
hx
hx
hy
hy
hx
k 2 xi , y j 1/ 2 k 2 xi , y j 1/ 2 k1 xi 1/ 2 , y j k1 xi 1/ 2 , y j hx hy qij vi , j
hy
hx
hx
hy
h
h
x k 2 xi , y j 1/ 2 vi , j 1 hx hy f ij y k1 xi 1/ 2 , y j 2 y j ,
hy
hx
am wm L bm wm 1 cm wm em wm L gm ,
g m hx hy fij
hy
hx
k1 xi 1 / 2 , y j 2 y j ,

15. Понижение размерности за счёт исключения известных значений

j 1; i 1;
h
h
h
h
x k 2 xi , y j 1/ 2 x k 2 xi , y j 1/ 2 y k1 xi 1/ 2 , y j y k1 xi 1/ 2 , y j hx hy qij vi , j
hy
hx
hx
hy
h
h
h
h
y k1 xi 1/ 2 , y j vi 1, j x k 2 xi , y j 1/ 2 vi , j 1 hx hy f ij x k 2 xi , y j 1/ 2 3 xi y k1 xi 1/ 2 , y j 1 y j
hx
hy
hy
hx
cm wm d m wm 1 em wm L g m ,
g m hx hy fij
h
hx
k2 xi , y j 1 / 2 3 xi y k1 xi 1 / 2 , y j 1 y j
hy
hx
j N y 1; i 1;
hx
k 2 xi , y j 1/ 2 vi , j 1
hy
h
h
h
h
x k 2 xi , y j 1/ 2 x k 2 xi , y j 1/ 2 y k1 xi 1/ 2 , y j y k1 xi 1/ 2 , y j hx hy qij vi , j
hy
hx
hx
hy
h
h
h
y k1 xi 1/ 2 , y j vi 1, j hx hy f ij y k1 xi 1/ 2 , y j 1 y j x k 2 xi , y j 1/ 2 4 xi
hx
hx
hy
am wm L cm wm dm wm 1 gm ,
g m hx hy fij
hy
hx
k1 xi 1 / 2 , y j 1 y j
hx
k2 xi , y j 1 / 2 4 xi
hy

16. Понижение размерности за счёт исключения известных значений

j 1; i N x 1;
hy
hx
k1 xi 1/ 2 , y j vi 1, j
h
h
h
h
x k 2 xi , y j 1/ 2 x k 2 xi , y j 1/ 2 y k1 xi 1/ 2 , y j y k1 xi 1/ 2 , y j hx hy qij vi , j
hy
hx
hx
hy
h
hx
h
k 2 xi , y j 1/ 2 vi , j 1 hx hy f ij x k 2 xi , y j 1/ 2 3 xi y k1 xi 1/ 2 , y j 2 y j
hy
hy
hx
hy
hx
g
h
h
f
k
x
,
y
x
k1 xi 1 / 2 , y j 2 y j
bm wm 1 cm wm em wm L g m ,
m
x y ij
2 i
j 1 / 2 3 i
hy
hx
j N y 1; i N x 1;
h
hx
k 2 xi , y j 1/ 2 vi , j 1 y k1 xi 1/ 2 , y j vi 1, j
hy
hx
h
h
h
h
x k 2 xi , y j 1/ 2 x k 2 xi , y j 1/ 2 y k1 xi 1/ 2 , y j y k1 xi 1/ 2 , y j hx hy qij vi , j
hy
hx
hx
hy
h
h
hx hy f ij y k1 xi 1/ 2 , y j 4 y j x k 2 xi , y j 1/ 2 4 xi
hx
hy
am wm L bm wm 1 cm wm g m ,
gm
hy
hx
k1 xi 1 / 2 , y j 4 y j
hx
k2 xi , y j 1 / 2 4 xi
hy

17. Понижение размерности за счёт исключения известных значений

*
*
7
8
9
12 13 14 17 18 19
1
2
3
4
*
*
*
5
6
7
8
9
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

18. Постановка задачи с граничными условиями первого и третьего рода

u
u
k1 x, y
q x, y u f x, y
k 2 x, y
x y
y
x
x a,b ,
0 c11 k1 x, y c12 ,
y c, d ,
0 c21 k2 x, y c22 ,
u x a 1 y ,
- k1
u
2 u x b 2 y ,
x x b
u y c 3 x ,
- k2
u
4 u y d 4 x
y y d

19. Сетка

xi a ihx ,
y j c jhy ,
xi 1 / 2
y j 1/ 2
xi xi 1
,
2
y j y j 1
2
i 0,1,..., N x
hx
b a
,
Nx
j 0,1,..., N y
hy
d c
Ny

20. Разностная схема для внутренних точек

i 1,..., N x 1;
j 1,..., N y 1;
vi 1, j vi , j
vi , j vi 1, j
h y k1 xi 1 / 2 , y j
h y k1 xi 1 / 2 , y j
h
h
x
x
h k x , y
x
2
i
j 1 / 2
v
i , j 1
vi , j
hy
h k x , y
x
2
i
v v
i, j
j 1 / 2
hy
i , j 1
hx h y qij vij hx h y f ij

21. Разностная схема для граничных условий по x

i 0; j 0;
vij 1 y j ,
1 y j 3 xi ,
i 0; j 1,..., N y ;
vij 1 y j ,
i N x ; j 1,..., N y 1;
vi , j vi 1, j
hy 2 y j vi , j 2 y j hy k1 xi 1/ 2 , y j
hx
hx
vi , j 1 vi , j hx
vi , j vi , j 1 hx
hx
k 2 xi , y j 1/ 2
k 2 xi , y j 1/ 2
hy qi , j vi , j hy f i , j
2
hy
2
hy
2
2

22. Разностная схема для граничных условий по y

i 1,..., N x ; j 0;
uij 3 xi ,
i 1,..., N x 1; j N y
vi 1, j vi , j hy
vi , j vi 1, j
hy
k1 xi 1/ 2 , y j
k1 xi 1/ 2 , y j
hx 4 xi vi , j 4 xi
hx
2
hx
2
vi , j vi , j 1
hy
hy
hx k 2 xi , y j 1/ 2
hx
qi , j vi , j hx
fi, j
hy
2
2

23. Разностная схема для угловой точки

i Nx;
j Ny
hy
vi , j vi 1, j
hy
2 y j vi , j 2 y j k1 xi 1/ 2 , y j
2
hx
2
hx hy
vi , j vi , j 1 hx hy
hx
hx
4 xi vi , j 4 xi k 2 xi , y j 1/ 2
qi , j vi , j
fi, j
2
2
hy
2 2
2
2

24. Разностная схема с приведёнными подобными членами

j 1,..., N y 1;
i 1,..., N x 1;
h
hx
k 2 xi , y j 1/ 2 vi , j 1 y k1 xi 1/ 2 , y j vi 1, j
hy
hx
hx
hy
hy
hx
k 2 xi , y j 1/ 2 k 2 xi , y j 1/ 2 k1 xi 1/ 2 , y j k1 xi 1/ 2 , y j hx hy qij vi , j
hy
hx
hx
hy
hy
hx
k1 xi 1/ 2 , y j vi 1, j
hx
k 2 xi , y j 1/ 2 vi , j 1 hx hy f ij
hy

25. Разностная схема с приведёнными подобными членами

i N x ; j 1,..., N y 1;
hy
hx
k 2 xi , y j 1/ 2 vi , j 1 k1 xi 1/ 2 , y j vi 1, j
2hy
hx
h
h
h
h
x k 2 xi , y j 1/ 2 x k 2 xi , y j 1/ 2 y k1 xi 1/ 2 , y j hy 2 y j x hy qij vi , j
2hy
hx
2
2hy
h
h
x k 2 xi , y j 1/ 2 vi , j 1 x hy f ij hy 2 y j
2hy
2

26. Разностная схема с приведёнными подобными членами

i 1,..., N x 1; j N y
hy
hx
k 2 xi , y j 1/ 2 vi , j 1
k1 xi 1/ 2 , y j vi 1, j
hy
2hx
h
h
h
h
x k 2 xi , y j 1/ 2 hx 4 xi y k1 xi 1/ 2 , y j y k1 xi 1/ 2 , y j hx y qij vi , j
2hx
2hx
2
hy
h
h
y k1 xi 1/ 2 , y j vi 1, j hx y f ij hx 4 xi
2hx
2

27. Разностная схема с приведёнными подобными членами

i Nx; j Ny;
hy
hx
k 2 xi , y j 1/ 2 vi , j 1
k1 xi 1/ 2 , y j vi 1, j
2hy
2hx
hx
hy
hy
hx
hx hy
k 2 xi , y j 1/ 2 4 xi
k1 xi 1/ 2 , y j 2 y j
qij vi , j
2
2hx
2
2 2
2hy
hy
hx hy
hx
f ij 4 xi 2 y j
2 2
2
2

28. Приведённый индекс. Переход к одному индексу

j 0,1,..., N y ;
i 0,1,..., N x ;
m jL i 1,
vi , j 1 wm L
vi 1, j wm 1
vi , j wm
vi 1, j wm 1
vi , j 1 wm L
L N x 1

29. Приведённый индекс. Переход к одному индексу

j 1,..., N y 1;
i 1,..., N x 1;
m jL i 1,
am wm L bm wm 1 cm wm d m wm 1 em wm L g m ,
am
bm
cm
hx
k 2 xi , y j 1/ 2 ,
hy
hy
hx
k1 xi 1 / 2 , y j
hy
hy
hx
h
k 2 xi , y j 1 / 2 x k 2 xi , y j 1 / 2 k1 xi 1 / 2 , y j k1 xi 1 / 2 , y j hx h y qij vij
hy
hy
hx
hx
dm
hy
hx
em
k1 xi 1 / 2 , y j
hx
k 2 xi , y j 1/ 2
hy
g m hx hy f ij

30. Приведённый индекс. Переход к одному индексу

i 0;
j 0,1,..., N y ;
m jL i 1,
cm wm g m ,
i N x ; j 1,..., N y 1;
m jL i 1,
am wm L bm wm 1 cm wm 0 wm 1 em wm L g m ,

31. Приведённый индекс. Переход к одному индексу

i 1,..., N x ; j 0;
cm wm g m ,
i 1,..., N x 1; j N y
am wm L bm wm 1 cm wm d m wm 1 0 wm L g m ,
i Nx; j Ny;
am wm L bm wm 1 cm wm 0 wm 1 0 wm L g m ,

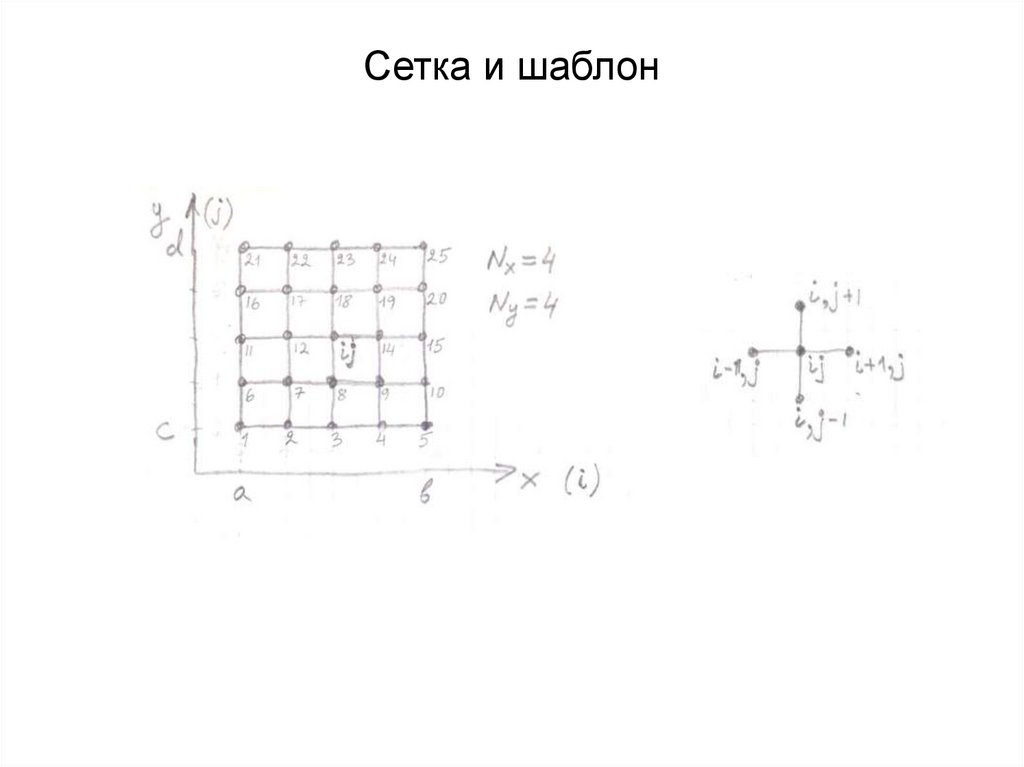
32. Сетка и шаблон

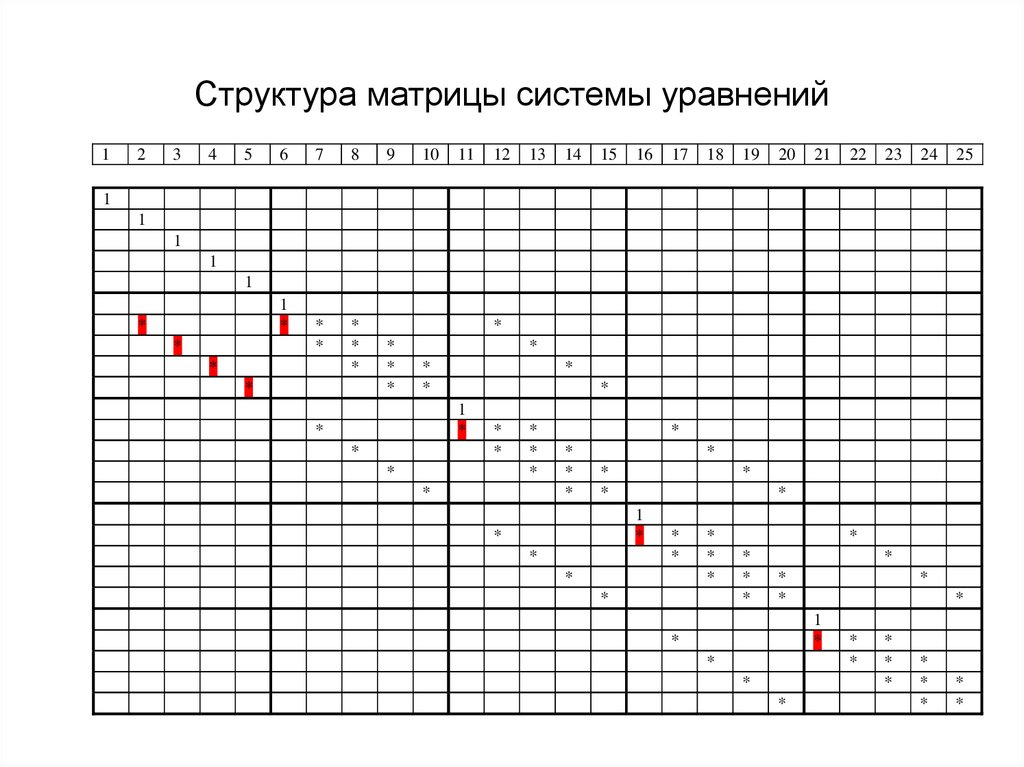
33. Структура матрицы системы уравнений

1
2
3
4
5
6
7
8
*
*
*
*
*
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
1
1
1
1
1
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

34. Структура матрицы системы уравнений

1
2
3
4
5
6
7
8
*
*
*
*
*
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
1
1
1
1
1
1
*
*
*
*
*
*
*
*
*
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
1
*
*
*
*
*
*
*
*
*
*
*
*
*
*

35. Структура матрицы системы уравнений

1
2
*
*
*
*
*
3
4
5
6
7
8
9
10 11 12 13 14 15 16
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
m j 1 L i,
L Nx
*
j 1,2,..., N y ;
i 1,2,..., N x ;
*
*

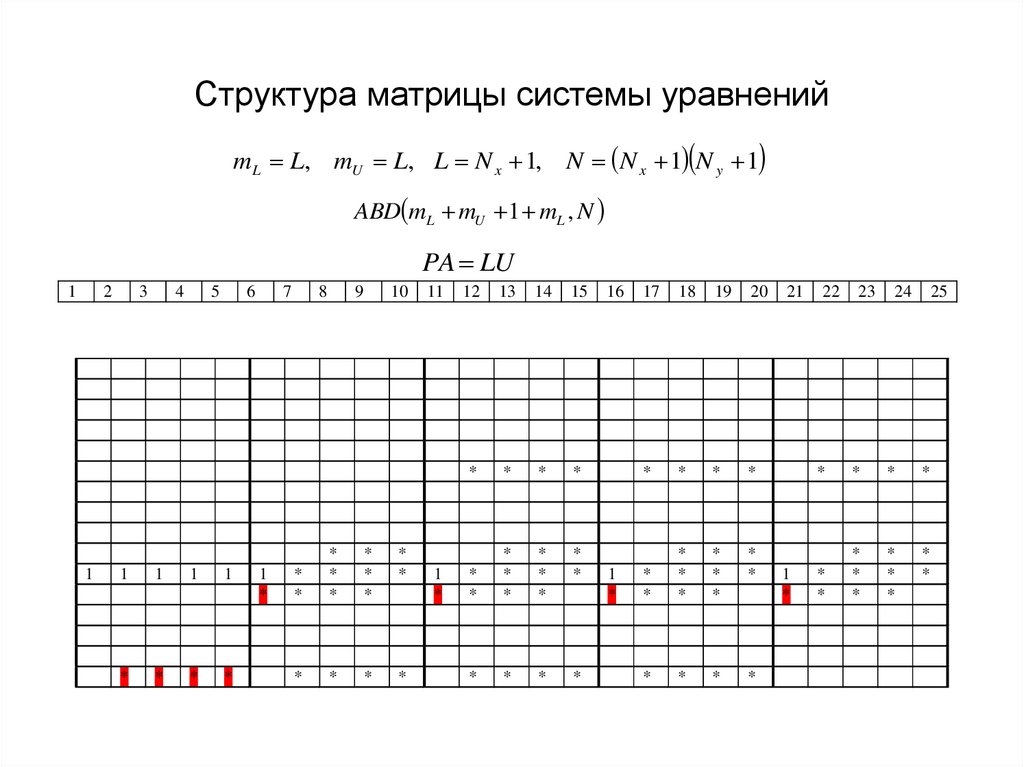
36. Структура матрицы системы уравнений

mL L, mU L, L N x 1, N N x 1 N y 1
ABD mL mU 1 mL , N
PA LU
1
2
1
3
4
5
6
1
1
1
1
*
*
*
*
7
1
*
8
9
10
*
*
*
*
*
*
*
*
*
*
*
*
*
*
11
1
*
12
13
14
15
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
16
1
*
17
18
19
20
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
21
1
*
22
23
24
25
*
*
*
*
*
*
*
*
*
*
*
*
*
*

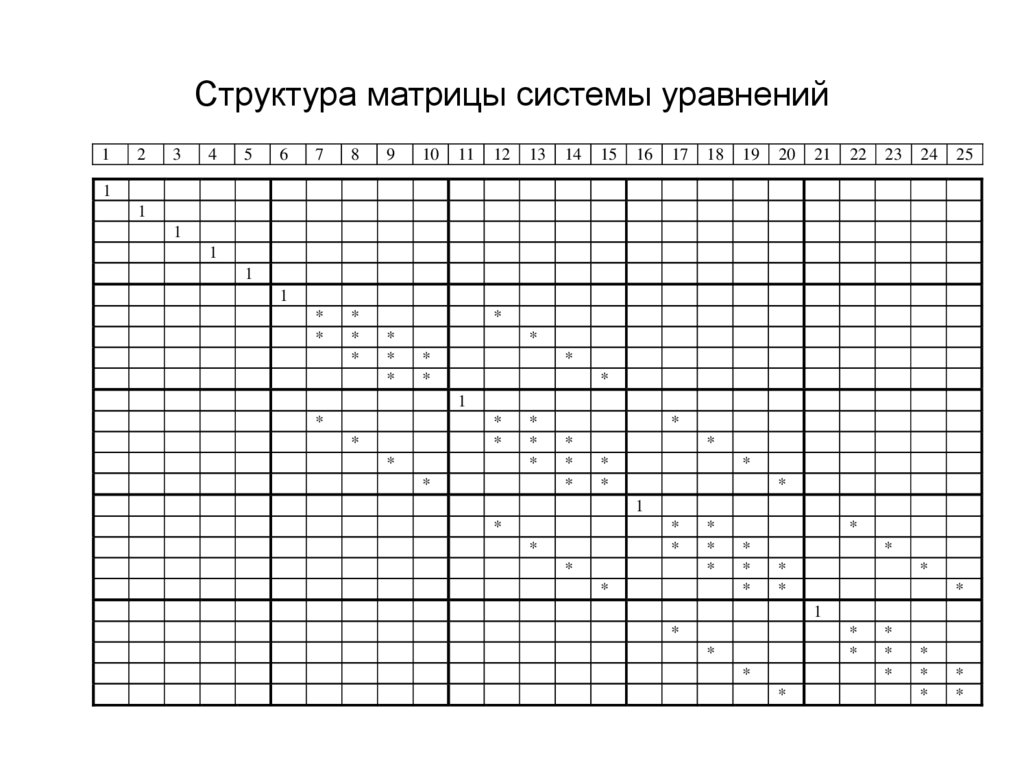
37. Структура матрицы системы уравнений

L N x 1, N N x 1 N y 1
mU L,
ABD mU 1, N
1
1
1
2
3
1
4
1
5
1
6
1
7
*
8
*
*
9
*
*
10
*
*
11
1
A AT ,
12
13
14
15
*
*
*
*
*
*
*
*
*
*
*
A 0,
16
1
17
A LLT
18
19
20
21
*
*
*
*
*
*
*
*
*
*
*
22
1
23
24
25
*
*
*
*
*
*
*
*
*
*
*

38. Структура матрицы системы уравнений

*
*
Aj
.
.
.
,
*
*
Aj R N x 1 N x 1 ,
v0, j
v
1, j
.
V j .
,
.
vN x 1, j
v
N x , j
* *
* * *
. .
Cj
.
.
.
.
.
,
. .
* * *
* *
C j R N x 1 N x 1 ,
Vj R
N x 1
,
f 0, j
f
1
,
j
.
F j .
,
.
f N x 1, j
f
N x , j
*
*
Bj
.
.
.
,
*
*
B j R N x 1 N x 1 ,
Fj R N x 1,

39. Метод матричной прогонки

C jV j B jV j 1
Fj ,
A jV j 1 C jV j B jV j 1 F j ,
Fj ,
A jV j 1 C jV j
j Ny
V j j 1V j 1 j 1 ,
j 0,1,2,...., N y 1
j 0
j 1,2, , N y 1
j и j свободные параметры (прогоночные коэффициен ты),
j R N 1 N 1 ,
x
j R N 1,
x
x
V j C j 1B jV j 1 C j 1Fj ,
j 1 C j 1B j ,
i 1 C j 1Fj ,
j 0
j 0

40. Метод матричной прогонки

V j 1 jV j j ,
j 1,2,...., N y 1
A C V B V
Aj jV j j C jV j B jV j 1 Fj ,
j
j
j
j
j
j 1
Fj Aj j ,
V j Aj j C j B jV j 1 Aj j C j Fj Aj j ,
1
1
j 1 Aj j C j 1 Fj Aj j ,
j 1 Aj j C j 1 B j ,
j 1,2,...., N y 1
V j 1 jV j j ,
A jV j 1 C jV j
j Ny 1
Fj ,
j Ny
V j Aj j C j Fj Aj j ,
1
j N y 1, N y 2,...,1,0,
V j j 1V j 1 j 1 ,
j Ny

41. Метод матричной прогонки

1 C0 1B0 ,
1 C0 1F0 ,
j 1,2,...., N y 1
j 1 Aj j C j 1 B j ,
j 1 Aj j C j 1 Fj Aj j ,
VN y AN y N y CN y
F A ,
~ N x3 N y
1
Ny
Ny
Ny
j N y 1, N y 2,...,1,0,
V j j 1V j 1 j 1 ,
det C j 0,
j 0,1,2,...., N y
i 1
C0 1B0 1,
C N 1y B N y 1,
det Aj j C j 0
C j 1 A j C j 1B j 1,