Похожие презентации:
1_3 Обратная и ранг
1.
§ 3. Обратная матрицаОпр.
1.
Квадратная
матрица
называется
невырожденной, если ее определитель не равен нулю
(det A ≠ 0). В противном случае (det A = 0) матрица A
называется вырожденной.
Опр. 2. Матрица A–1 называется обратной для
квадратной матрицы A, если A–1A = AA–1 = E, где E –
единичная матрица того же порядка, что и A.
Замечание. Понятие обратной матрицы вводится
только для квадратных матриц.
2.
Тh1(необходимое
и
достаточное
условие
существования обратной матрицы). Матрица A имеет
обратную матрицу A–1 тогда и только тогда, когда
матрица A невырожденная (т. е. det A ≠ 0).
Доказательство. Необходимость.
Докажем, что если A–1 существует, то det A ≠ 0.
По опр., A–1A = E.
По th1 § 2, det A–1A = det A–1 det A.
1 и
Следовательно, det A–1 det A =1, откуда det A 1
det A
det A ≠ 0.
3.
Достаточность. Покажем, что обратная матрицаможет быть найдена по формуле
1
1
A
S TA ,
(1)
det A
где SA – матрица, составленная из алгебраических
дополнений к элементам матрицы A, т. е.
A11
A
S A 21
...
An1
A12
A22
...
An 2
... A1n
... A2 n
.
... ...
... Ann
Для этого покажем, что матрица A–1, определенная
формулой (1), удовлетворяет соотношениям A–1A = E и
AA–1 = E.
4.
A11A
1 12
1
A A
det A ...
A1n
A21
A22
...
A2 n
... An1 a11
... An 2 a21
... ... ...
... Ann an1
a12
a22
...
an 2
... a1n
... a2 n
.
... ...
... ann
cij A1i a1 j A2i a2 j ... Ani anj ,
По свойствам определителей, cij = 0, если i ≠ j, и cii = det A.
0
det A
0
det A
1
1
A A
...
det A ...
0
0
...
0 1
...
0 0
...
... ...
... det A 0
0
1
...
0
...
...
...
...
Аналогично доказывается, что AA–1 = E. ◄
0
0
E.
...
1
5.
1 2 1–1
Пример 1. Найдем A , если A 4 3 2 .
5 2 3
1 2 1
3 2
4 2
4 3
2
1
det A 4 3 2 1
2 3
5 3
5 2
5 2 3
9 4 2 (12 10) 8 15 2 0,
6.
1 2 1–1
Пример 1. Найдем A , если A 4 3 2 .
5 2 3
det A 2.
A11
1
−1














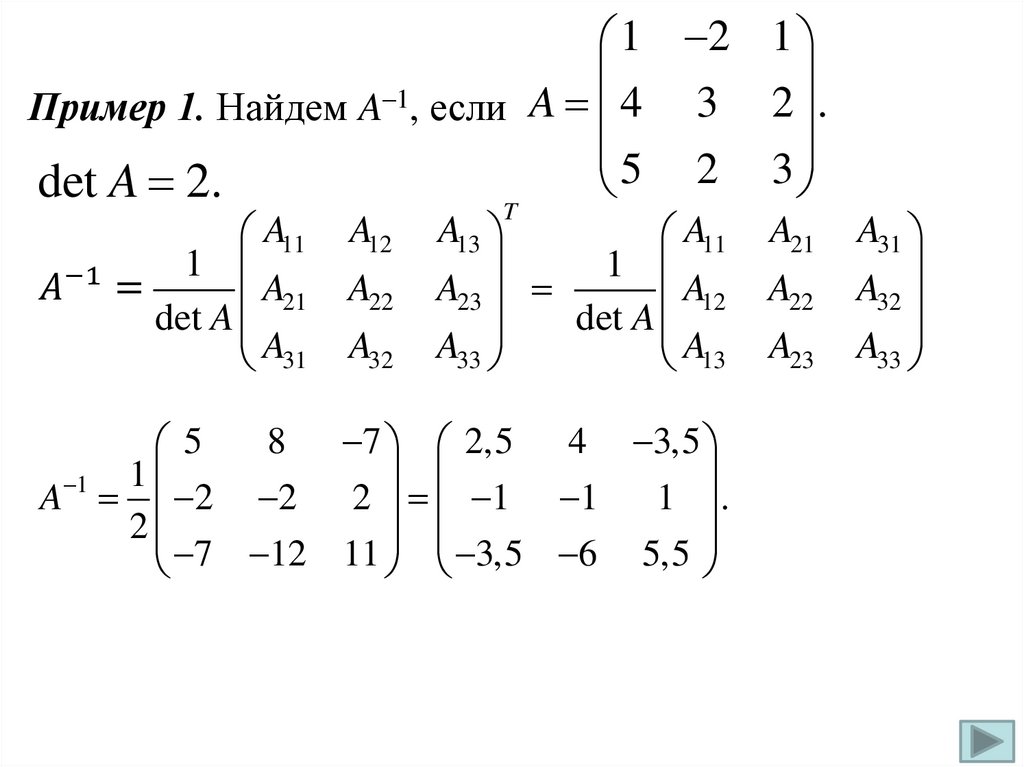












 Математика
Математика








