09 PiN-1

1.

2. 4. Предел и непрерывность функций

4. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ
ФУНКЦИЙ
4.1 Функция. Основные понятия и свойства
4.2 Предел функции
4.3 Непрерывность функции

3. 4. Предел и непрерывность функций

4. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ
ФУНКЦИЙ
4.1 Функция. Основные понятия и свойства
4.1.1. Понятие функции
4.1.2. Основные свойства функций
4.1.3. Основные элементарные функции и их
графики
4.1.4. Сложная функция
4.1.5. Элементарные функции
4.1.6. Алгебраические и трансцендентные функции
4.1.7. Преобразования графика функции

4. 4.1.1. Понятие функции

4.1.1. ПОНЯТИЕ ФУНКЦИИ
Правило (закон), которое каждому элементу х из множества X R
сопоставляет единственный элемент у из множества Y R,
называется функцией одной действительной переменной.
Обозначения: f : X Y или y = f(x), x X.
зависимая переменная
или функция
независимая переменная
или аргумент
Множество Х называется областью определения функции f и
обозначается D(f).
Множество E(f) = { y Y : y = f(x), x X } называется множеством
значений функции f.
значение функции f в точке х
Если число хₒ D(f) , то говорят, что функция f определена в точке хₒ ,
то есть f(хₒ) можно найти.

5. 4.1.1. Понятие функции

4.1.1. ПОНЯТИЕ ФУНКЦИИ
Способы задания функции
1) Аналитический.
Функция y = f(x) задана аналитически, если с помощью одной или
нескольких формул устанавливается порядок вычисления значения
функции для каждого значения аргумента.
Примеры
1)
2)
y x2 5
sin x cos x
f ( x)
x 1
S (r ) r 2
x при x 0,
f ( x)
при x 0.
x
3)
4)
2) Табличный.
При этом способе выписываются в определенном порядке значения
аргумента и соответствующие им значения функции.
x
x1
x2
…
xn
у
y1
y2
…
yn

6. 4.1.1. Понятие функции

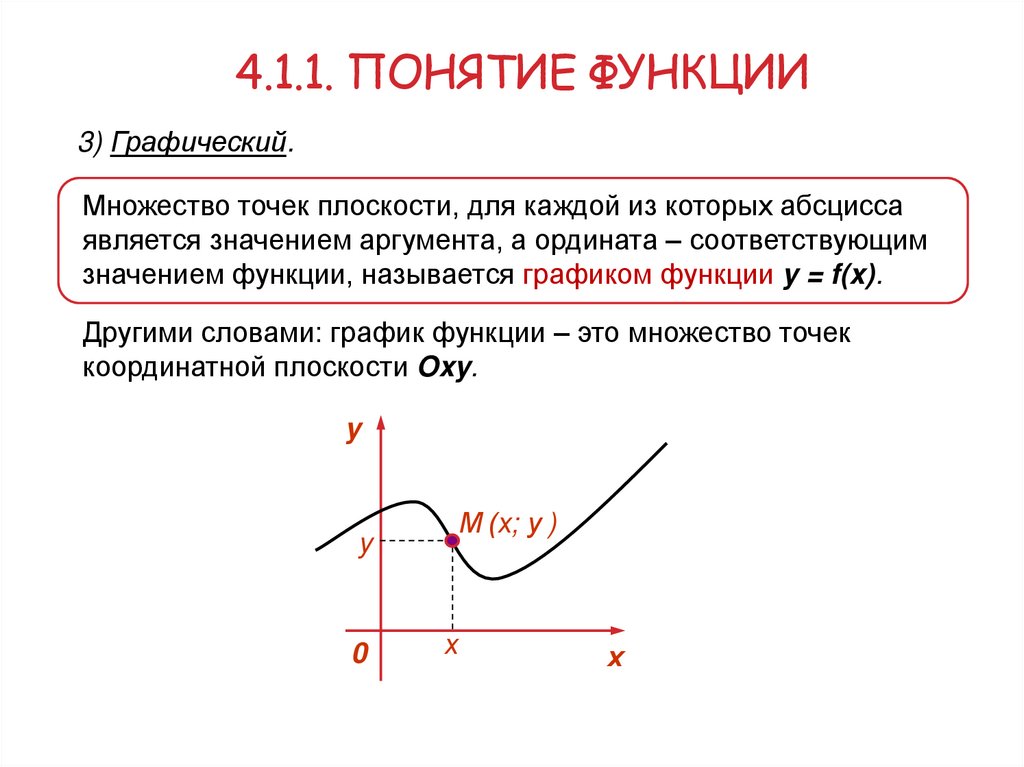
4.1.1. ПОНЯТИЕ ФУНКЦИИ
3) Графический.
Множество точек плоскости, для каждой из которых абсцисса
является значением аргумента, а ордината – соответствующим
значением функции, называется графиком функции y = f(x).
Другими словами: график функции – это множество точек
координатной плоскости Oxy.
y
y
0
М (х; у )
х
х

7. 4.1.2. Основные свойства функций

4.1.2. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
Функция y = f(x), определенная на множестве D(f), называется
четной, если для любого x, принадлежащего D(f) выполняются
условия: -x также принадлежит D(f) и f(-x ) = f(x).
x D( f )
x D( f ) :
f ( x) f ( x)
Функция y = f(x), определенная на
множестве D(f), называется нечетной, если: x D( f ) :
x D( f )
f ( x) f ( x)
График четной функции симметричен относительно оси Oy.
График нечетной функции симметричен относительно точки O(0; 0).
y
y
3
y x
y x2
0
0
х
х

8. 4.1.2. Основные свойства функций

4.1.2. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
Пусть функция y = f(x) определена на множестве D(f) и пусть D1 D(f).
Если
x1, x2 D1; x1 x2 f ( x1 ) f ( x2 )
y
то функция называется возрастающей.
Если x1, x2 D1; x1 x2 f ( x1 ) f ( x2 ) f(x12 )
то функция называется убывающей.
Если
x1, x2 D1;
f(x )
21
Из неравенства
x1 < x2
x1 x2 f ( x1 ) следует
f ( x2 ) неравенство
x1 xx22
f(x1) <0f(x2)
х
то функция называется неубывающей.
Если
x1, x2 D1; x1 x2 f ( x1 ) f ( x2 )
то функция называется невозрастающей.
Возрастающие, убывающие, невозрастающие и неубывающие функции
называются монотонными на множестве D1, интервал, на котором
функция монотонна называется интервалом монотонности.
Возрастающие и убывающие функции называются строго монотонными.

9. 4.1.2. Основные свойства функций

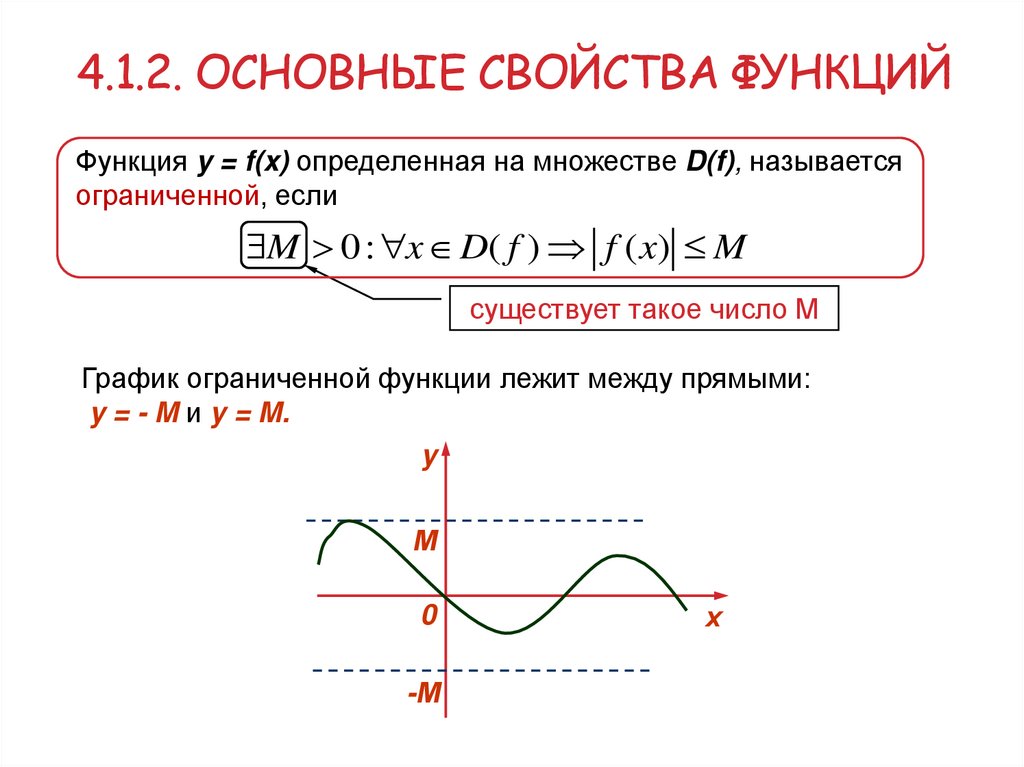
4.1.2. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
Функция y = f(x) определенная на множестве D(f), называется
ограниченной, если
M 0 : x D( f ) f ( x) M
существует такое число М
График ограниченной функции лежит между прямыми:
y = - M и y = M.
y
М
0
-М
х

10. 4.1.2. Основные свойства функций

4.1.2. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
Функция y = f(x) определенная на множестве D(f), называется
ограниченной сверху, если
M : x D( f ) f ( x) M
Функция y = f(x) определенная на множестве D(f), называется
ограниченной снизу, если
m : x D( f ) f ( x) m
Примеры
Определить, является ли функция ограниченной:
1)
y x2
3)
y 5 x2
5)
y cos x 3
2)
y sin x
4)
y 2x
6)
y 4 x
1), 4), 6) – ограничены снизу;
3) – ограничена сверху;
2), 5) – ограничены.

11. 4.1.2. Основные свойства функций

4.1.2. ОСНОВНЫЕ СВОЙСТВА ФУНКЦИЙ
Функция y = f(x) определенная на множестве D(f), называется
x T D( f )
периодической, если T 0 : x D( f )
f ( x T ) f ( x)
Число Т называется периодом
функции.
Если Т – период функции, то ее
периодами будут также числа
2Т, 3Т и так далее.
Наименьшее положительное число Т,
удовлетворяющее условию:
f(x +T) = f(x), называется основным
периодом
y
Т
х
0
2Т

12. 4.1.3. Основные элементарные функции и их графики

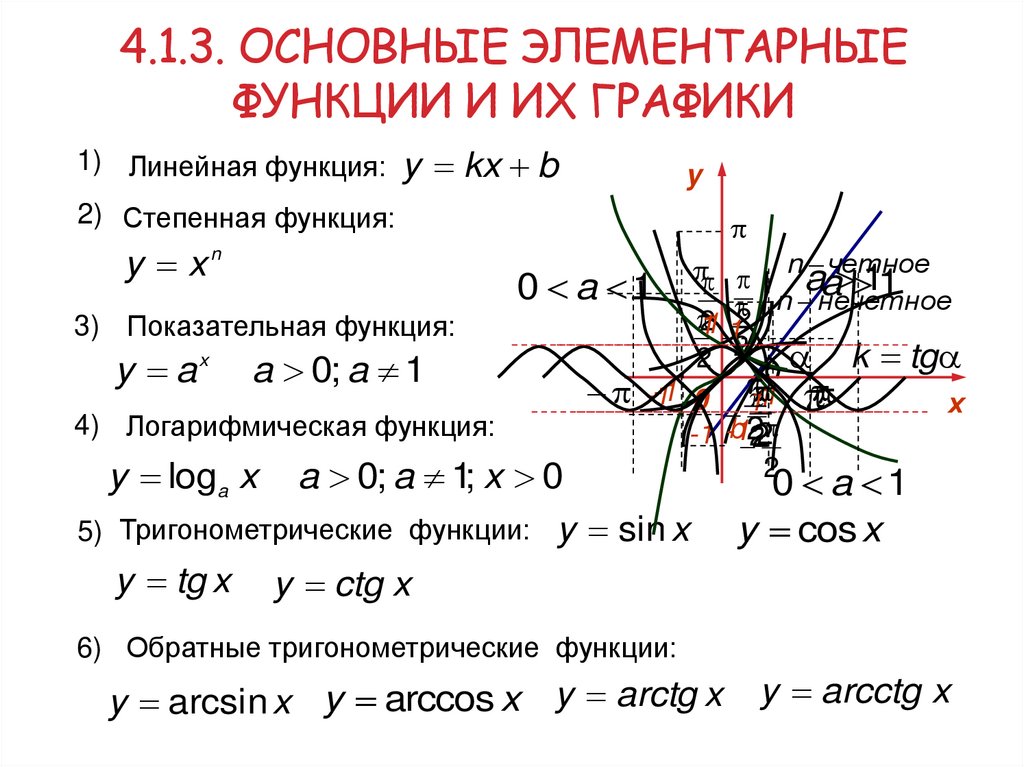
4.1.3. ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ
ФУНКЦИИ И ИХ ГРАФИКИ
1) Линейная функция: y kx b
y
2) Степенная функция:
y x
четное
n a
a 11
0 a 1
n
нечетное
1
21 1 2
3) Показательная функция:
x
2 2 k tg
y a
a 0; a 1
1
-1 0
-1
1
1
х
4) Логарифмическая функция:
b2
-1 -1
222
2
y log x a 0; a 1; x 0
n
a
5) Тригонометрические функции:
y tg x
y sin x
0 a 1
y cos x
y ctg x
6) Обратные тригонометрические функции:
y arcsin x y arccos x y arctg x
y arcctg x

13. 4.1.4. Сложная функция

4.1.4. СЛОЖНАЯ ФУНКЦИЯ
Если y является функцией от u, а u в свою очередь зависит от
переменной x, то y также зависит от x.
y f (u )
u ( x)
сложная функция
(суперпозиция функций)
Областью определения функции y f ( x) является или вся
область определения функции u(x) или та ее часть, в которой
определяются значения u, не выходящие из области определения
функции f(u).

14. 4.1.4. Сложная функция

4.1.4. СЛОЖНАЯ ФУНКЦИЯ
Пример
Даны функции
f ( x) log3 x, g ( x) x.
Записать следующие суперпозиции:
f g ( x) , g f ( x) , f f ( x) , g g ( x) .
f g ( x) f
x log
3
1
x log 3 x
2
g f ( x) g log 3 x log 3 x
f f ( x) f log 3 x log 3 log 3 x
g g ( x) g
x
x 4x

15. 4.1.5. Элементарные функции

4.1.5. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Элементарной функцией называется функция, которая может
быть задана одной формулой вида y = f(x), где справа стоящее
выражение составлено из основных элементарных функций и
постоянных при помощи конечного числа операций сложения,
вычитания, умножения, деления и суперпозиции.
Пример
lg x 4 cos x 5
y x
10 x arcctg 3x
2

16. 4.1.6. Алгебраические и трансцендентные функции

4.1.6. АЛГЕБРАИЧЕСКИЕ И
ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
К числу алгебраических функций относятся элементарные
функции следующего вида:
1) Целая рациональная функция или многочлен:
y a0 x n a1x n 1 an
2) Дробная рациональная функция – отношение многочленов:
a0 x n a1x n 1 an
y
b0 x m b1x m 1 bm
3) Иррациональная функция:
Если в формуле y = f(x) в правой части производятся операции
сложения, вычитания, умножения, деления и возведения в степень с
рациональными нецелыми показателями, то функция y = f(x)
называется иррациональной.
Пример
y x 5 x 15
Функция, не являющаяся алгебраической, называется
трансцендентной: y = cos x; y = ln x и так далее.
3
4

17. 4.1.7. Преобразования графика функции

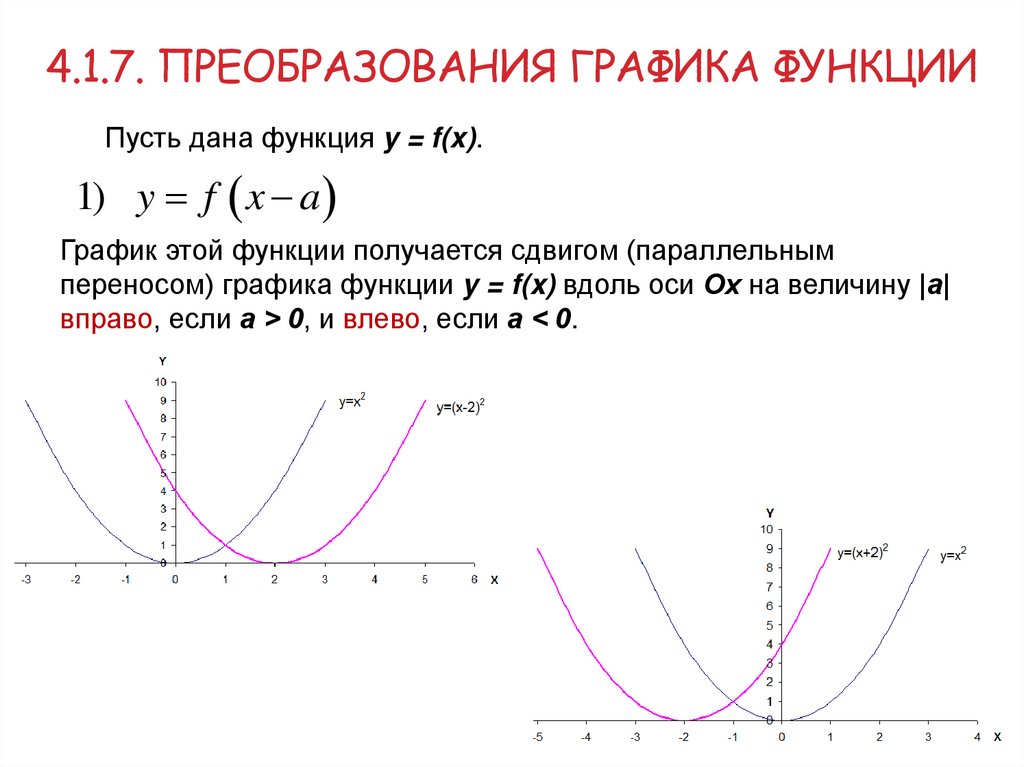
4.1.7. ПРЕОБРАЗОВАНИЯ ГРАФИКА ФУНКЦИИ
Пусть дана функция y = f(x).
1) y f x a
График этой функции получается сдвигом (параллельным
переносом) графика функции y = f(x) вдоль оси Ох на величину |а|
вправо, если а > 0, и влево, если а < 0.

18. 4.1.7. Преобразования графика функции

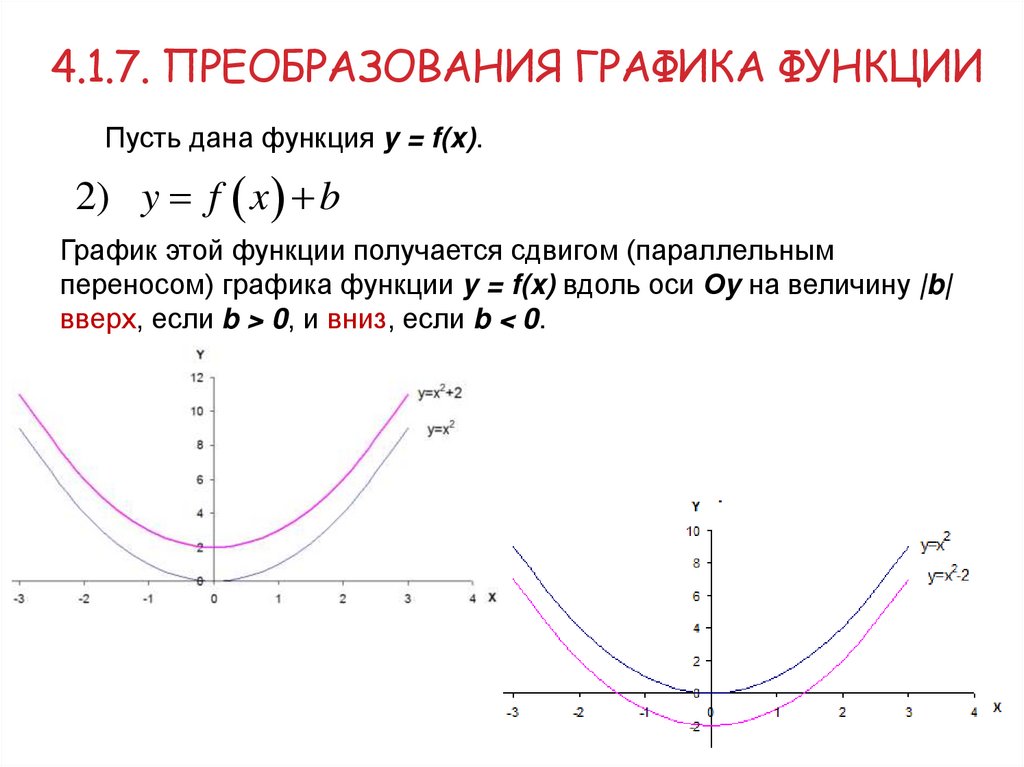
4.1.7. ПРЕОБРАЗОВАНИЯ ГРАФИКА ФУНКЦИИ
Пусть дана функция y = f(x).
2) y f x b
График этой функции получается сдвигом (параллельным
переносом) графика функции y = f(x) вдоль оси Оy на величину |b|
вверх, если b > 0, и вниз, если b < 0.

19. 4.1.7. Преобразования графика функции

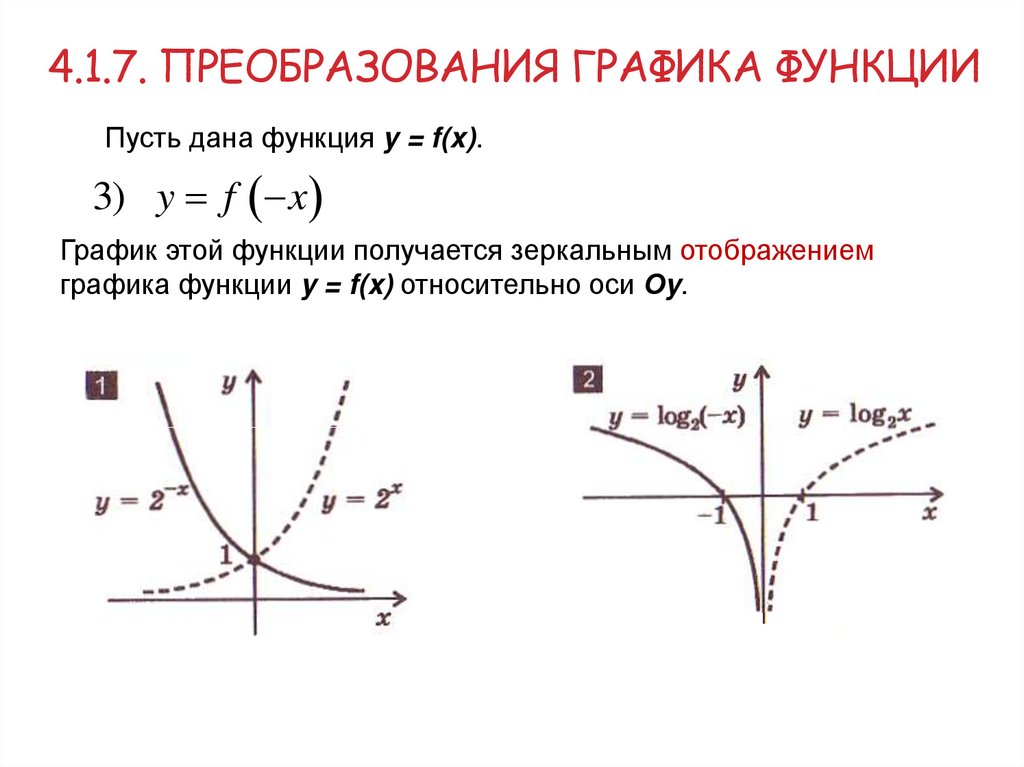
4.1.7. ПРЕОБРАЗОВАНИЯ ГРАФИКА ФУНКЦИИ
Пусть дана функция y = f(x).
3) y f x
График этой функции получается зеркальным отображением
графика функции y = f(x) относительно оси Оy.

20. 4.1.7. Преобразования графика функции

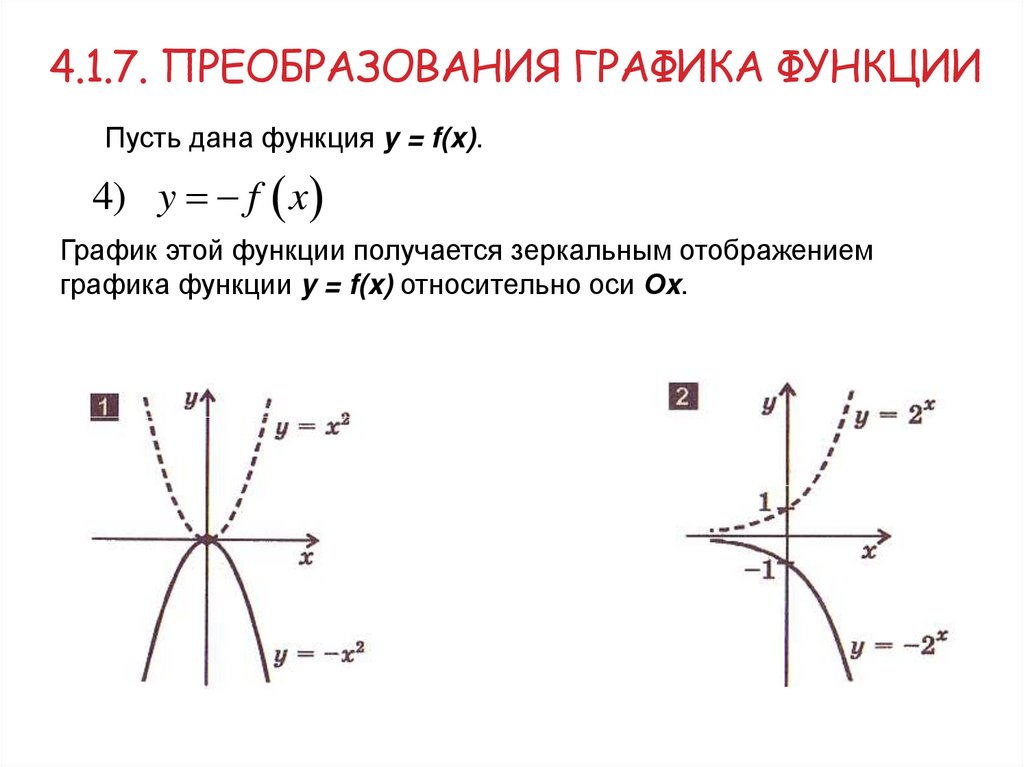
4.1.7. ПРЕОБРАЗОВАНИЯ ГРАФИКА ФУНКЦИИ
Пусть дана функция y = f(x).
4) y f x
График этой функции получается зеркальным отображением
графика функции y = f(x) относительно оси Оx.

21. 4.1.7. Преобразования графика функции

4.1.7. ПРЕОБРАЗОВАНИЯ ГРАФИКА ФУНКЦИИ
Пусть дана функция y = f(x).
5) y f x
График этой функции получается ( > 0) :
а) сжатием графика функции y = f(x) вдоль оси Оx в раз при > 1,
б) растяжением графика функции y = f(x) вдоль оси Оx в 1/ раз при < 1.

22. 4.1.7. Преобразования графика функции

4.1.7. ПРЕОБРАЗОВАНИЯ ГРАФИКА ФУНКЦИИ
Пусть дана функция y = f(x).
6) y f x
График этой функции получается ( > 0) :
а) растяжением графика функции y = f(x) вдоль оси Оy в раз при > 1,
б) сжатием графика функции y = f(x) вдоль оси Оy в 1/ раз при < 1.

23. 4.1.7. Преобразования графика функции

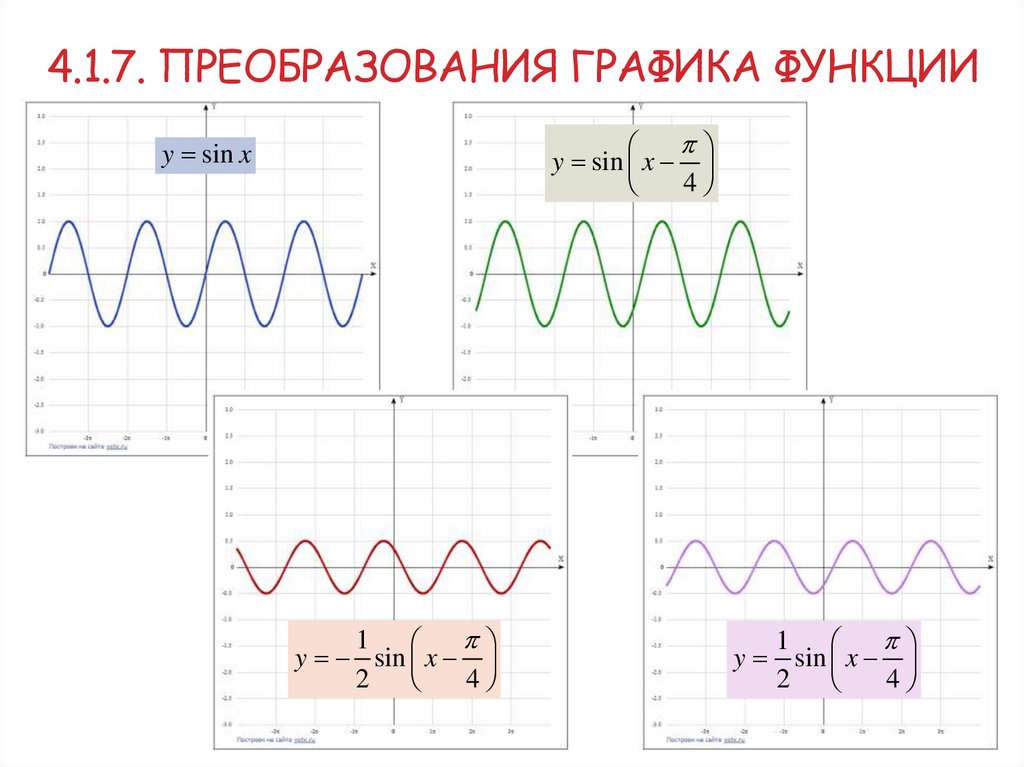
4.1.7. ПРЕОБРАЗОВАНИЯ ГРАФИКА ФУНКЦИИ
Вывод:
Путём простых преобразований графика исходной функции y = f(x)
можно построить график функции вида
y f x a b, где a, b, , R.
Пример
Построить график функции
1
y sin x .
2
4

24. 4.1.7. Преобразования графика функции

4.1.7. ПРЕОБРАЗОВАНИЯ ГРАФИКА ФУНКЦИИ
y sin x
4
y sin x
1
y sin x
2
4
1
y sin x
2
4

25. Продолжение следует...

ПРОДОЛЖЕНИЕ СЛЕДУЕТ...