Похожие презентации:
Понятие функции и способы задания
1. Лекция Функции
1 Понятие функции и способы задания2 Свойства функций
3 Элементарные функции
4 Последовательности
18 февраля 2024 г.
2. Эпиграф
Математический анализ неменее всеобъемлющ, чем сама
природа.
Ж.Фурье
Иванов О.В. Кудряшова Л.В. 2005
2
3. 1. Понятие функции и способы задания
ОпределениеЧетыре способа задания
18 февраля 2024 г.
4. Постоянные и переменные величины
Постоянной величиной (constant)сохраняющая одно и то же значение.
называется
величина,
Переменной величиной (variable quantity) называется
величина, которая может принимать различные значения.
Одна и та же величина может быть постоянной или переменной
в зависимости от рассматриваемой модели и желаний
исследователя.
Обозначения. Постоянные (a, b, c, d) и переменные (x, y, z, u, v).
Иванов О.В. Кудряшова Л.В. 2005
4
5. Что такое функция
И.Бернулли в 1718 году дал следующее определение:«Функцией переменной величины называется количество,
образованное каким угодно способом из этой переменной
величины и постоянных».
Эйлер в «Дифференциальном исчислении» пишет: «Величины,
зависящие от других так, что с изменением вторых меняются и
первые, принято называть их функциями».
Дирихле: «Переменная величина y называется функцией
переменной величины x, если каждому значению величины x
соответствует единственное определенное значение величины
y.
Иванов О.В. Кудряшова Л.В. 2005
5
6. Функция (function)
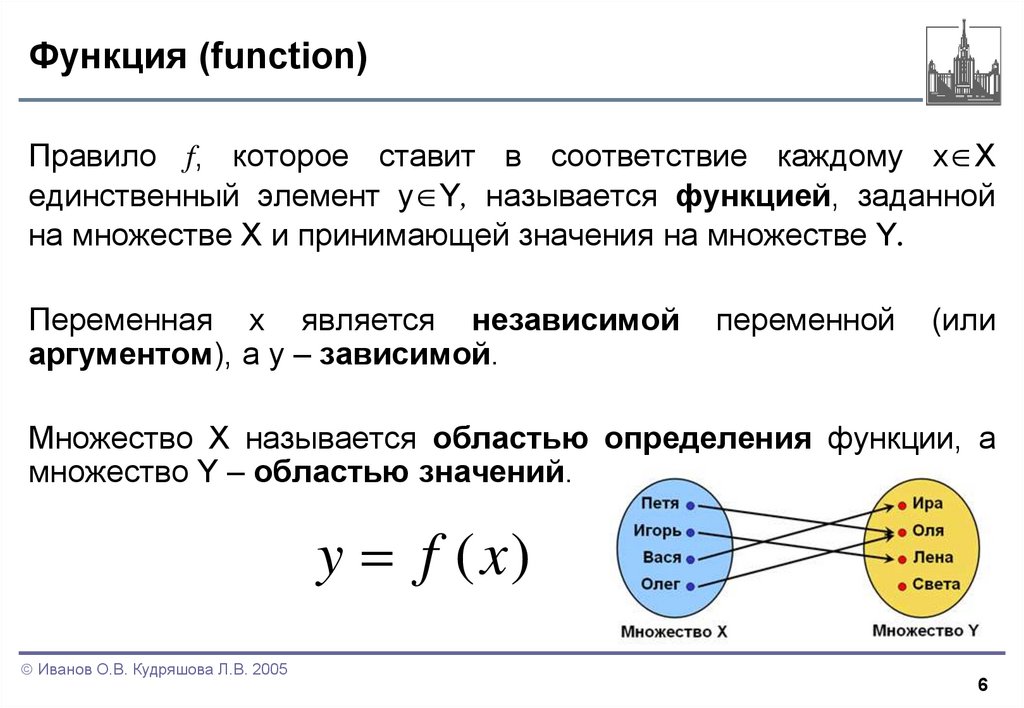
Правило f, которое ставит в соответствие каждому x Xединственный элемент y Y, называется функцией, заданной
на множестве X и принимающей значения на множестве Y.
Переменная x является независимой
аргументом), а y – зависимой.
переменной
(или
Множество X называется областью определения функции, а
множество Y – областью значений.
y f ( x)
Иванов О.В. Кудряшова Л.В. 2005
6
7. Задание функций
Задать функцию означает определить три объекта:1. Множество X
2. Множество Y
3. Правило f
f
X
Иванов О.В. Кудряшова Л.В. 2005
Y
7
8. Аналитический способ
Функция задана аналитически, если связь между функцией иаргументом задана формулой:
y f ( x)
Пример. Функция
Иванов О.В. Кудряшова Л.В. 2005
y x
2
8
9. Табличный способ
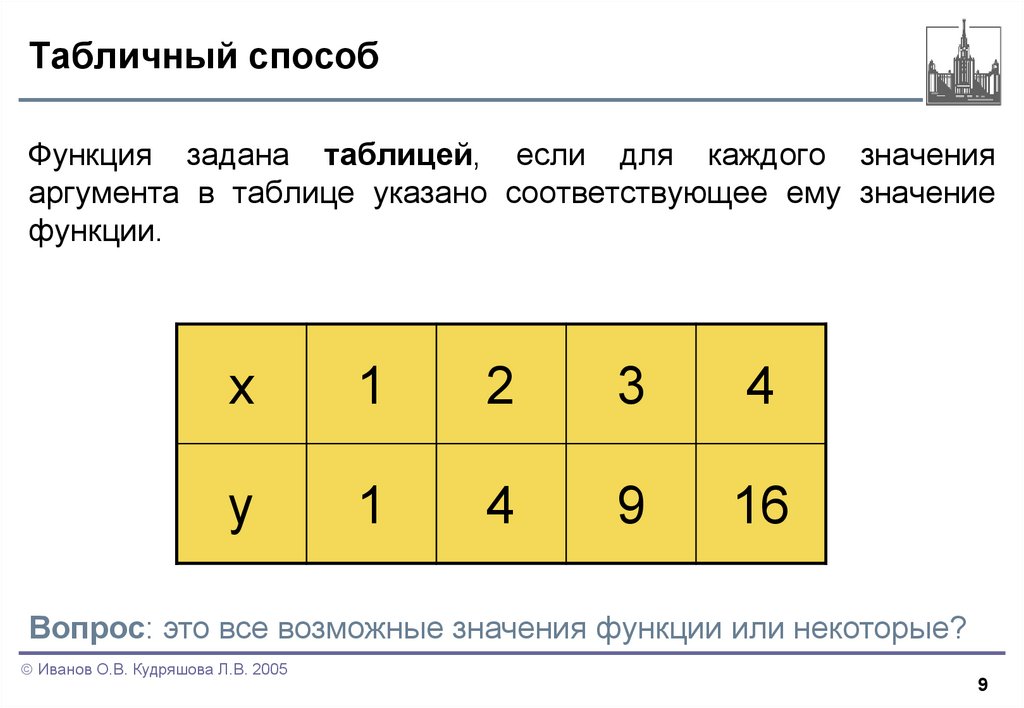
Функция задана таблицей, если для каждого значенияаргумента в таблице указано соответствующее ему значение
функции.
x
1
2
3
4
y
1
4
9
16
Вопрос: это все возможные значения функции или некоторые?
Иванов О.В. Кудряшова Л.В. 2005
9
10. Графический способ
Функция задана графически, если на плоскости изображеномножество точек с координатами (x, y), абсциссы которых есть
значения аргумента, а ординаты – соответствующие им
значения функции.
y
y f ( x)
0
Иванов О.В. Кудряшова Л.В. 2005
x
График не дает точного
представления о
функции, зато позволяет
ее «увидеть».
10
11. Описательный способ
Функция может быть задана словесно.Пример. Функция равна единице для всех рациональных
значений аргумента и равна нулю для иррациональных. Это
функция Дирихле. Ее можно записать иначе:
1, если x рационально
D( x )
0, если x иррационально
Иванов О.В. Кудряшова Л.В. 2005
11
12. Пример. Функция Филлипса
Как известно, цена труда зависит от конъюнктуры рынка. Когдана рынке труда имеет место дефицит, то рабочие могут
рассчитывать на большую зарплату, и наоборот, в период
существования конъюнктурной безработицы рабочим будут
платить меньше.
В 1958 году профессор Лондонской школы экономики Филлипс
опубликовал
результаты
своих
исследований
взаимозависимости между уровнем безработицы и изменением
денежной ставки зарплаты в Великобритании в период с 1861 до
1957 года.
Иванов О.В. Кудряшова Л.В. 2005
12
13. Пример. Функция Филлипса
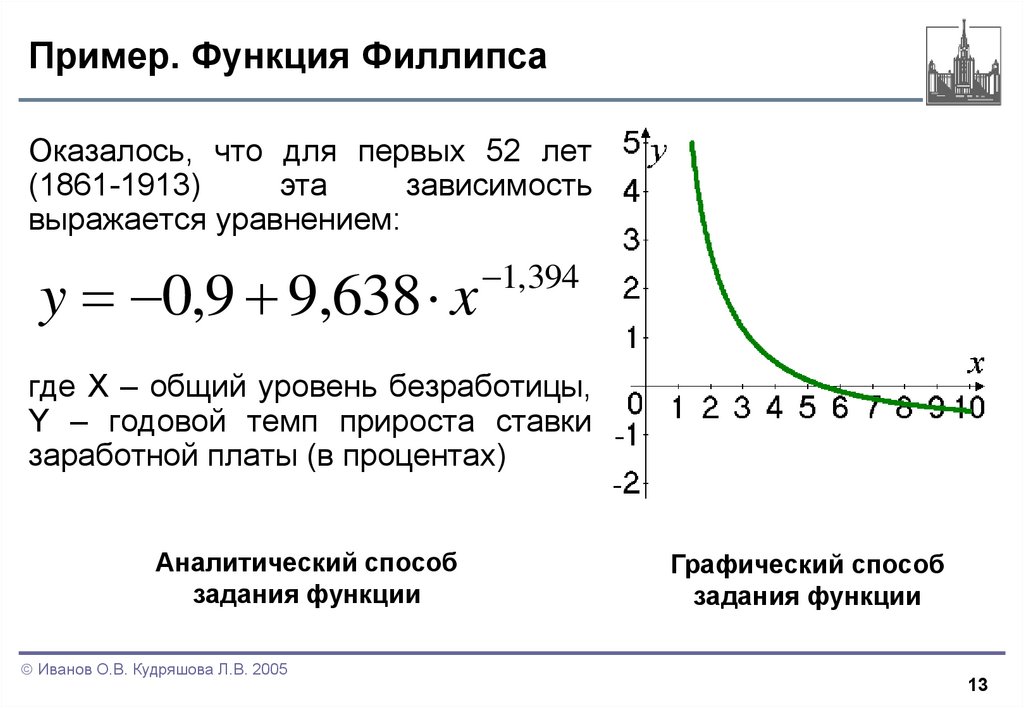
Оказалось, что для первых 52 лет(1861-1913)
эта
зависимость
выражается уравнением:
y 0,9 9,638 x
1,394
где X – общий уровень безработицы,
Y – годовой темп прироста ставки
заработной платы (в процентах)
Аналитический способ
задания функции
Иванов О.В. Кудряшова Л.В. 2005
Графический способ
задания функции
13
14. 2-2. Свойства функций
Шесть свойств, которыми могут обладатьфункции
Понятие обратной функции
18 февраля 2024 г.
15. Свойства функций
Под основными свойствами функций y = f (x) будем пониматьследующие шесть:
1) область определения D( f )
2) область значений E( f )
3) четность, нечетность
4) монотонность
5) ограниченность
6) периодичность
Иванов О.В. Кудряшова Л.В. 2005
15
16. Область определения
Функция y = f (x) задана, или определена, на множестве X.Множество X называется областью определения функции.
Пример. Найти область определения функции:
x 5
y
x 1
Решение. Функция существует для всех значений аргумента,
кроме x = 1. Область определения:
x ( ; 1) (1; )
Иванов О.В. Кудряшова Л.В. 2005
16
17. Область значений
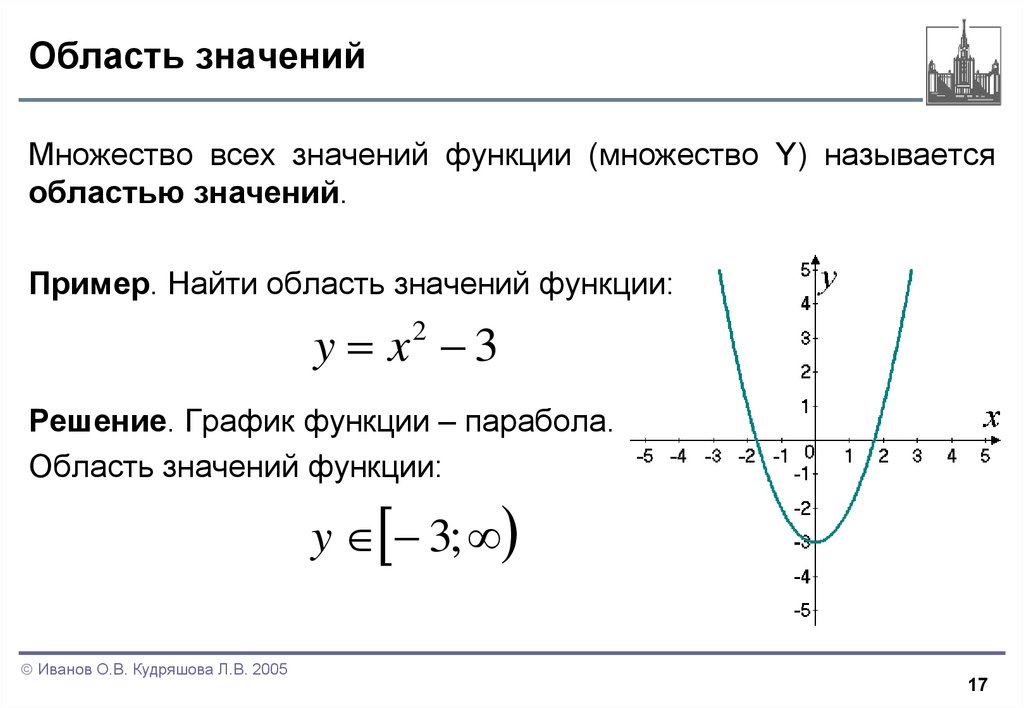
Множество всех значений функции (множество Y) называетсяобластью значений.
Пример. Найти область значений функции:
y x 3
2
Решение. График функции – парабола.
Область значений функции:
y 3;
Иванов О.В. Кудряшова Л.В. 2005
17
18. Четность, нечетность
Функция y = f (x) называется четной (even function), если длялюбого x из области определения:
f ( x) f ( x)
и нечетной (odd function), если :
f ( x) f ( x)
График
четной
функции
симметричен
относительно
вертикальной оси, график нечетной функции центрально
симметричен относительно начала координат.
Иванов О.В. Кудряшова Л.В. 2005
18
19. Примеры
Функция y = x2 – 1 четная, так как y(–x) = x2 – 1 = y(x). Графиксимметричен относительно вертикальной оси.
Функция y = x3 нечетная, так как y(–x) = (–x)3 = – y(x). График
центрально симметричен относительно начала координат.
Функция y = x2 - x + 2 не является ни четной, ни нечетной.
Такие функции называют иногда функциями общего вида.
Иванов О.В. Кудряшова Л.В. 2005
19
20. Возрастающая функция
Функция y = f (x) называется возрастающей на промежутке X,если для любых двух значений x1 и x2 из этого промежутка
большему значению аргумента соответствует большее значение
функции:
x2 x1
f ( x2 ) f ( x1 )
y
f(x2)
f(x1)
0
Иванов О.В. Кудряшова Л.В. 2005
x1
x2
x
Самостоятельно дайте
определение убывающей
функции, невозрастающей
функции.
20
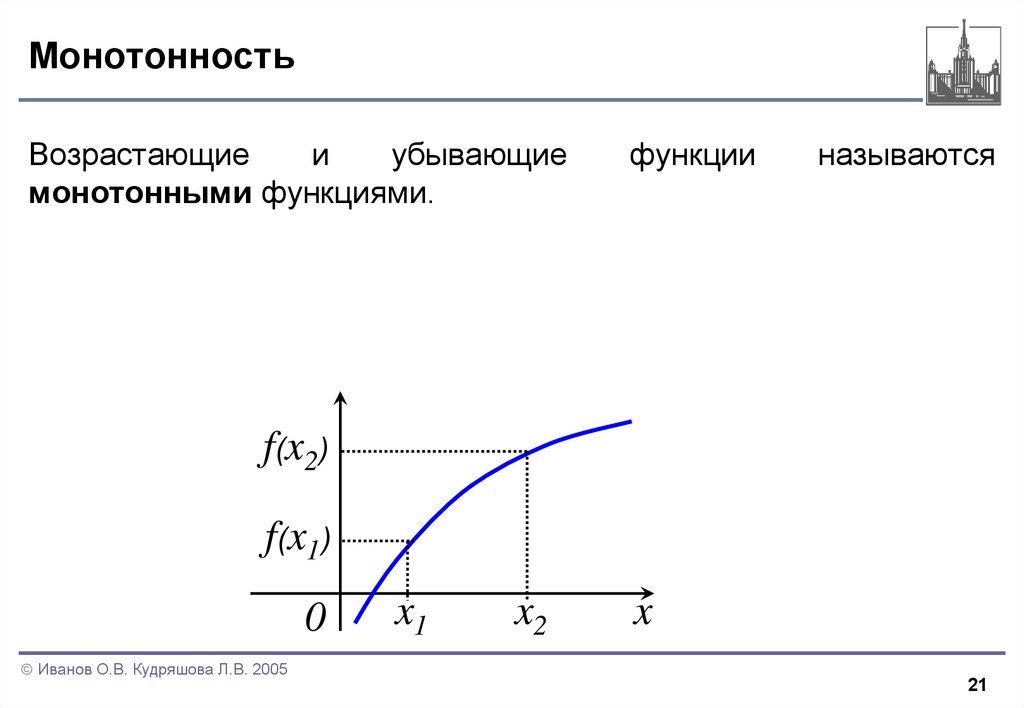
21. Монотонность
Возрастающиеи
убывающие
монотонными функциями.
функции
называются
f(x2)
f(x1)
0
Иванов О.В. Кудряшова Л.В. 2005
x1
x2
x
21
22. Ограниченность
Функция y = f (x) называется ограниченной на промежутке X,если существует такое положительное число M, что для любого
x X выполняется условие | f (x)| M. В противном случае
функция неограниченная.
Пример. Функция y = sin x является ограниченной на всей
числовой оси, поскольку выполняется условие:
| sin x | 1
Иванов О.В. Кудряшова Л.В. 2005
22
23. Периодичность
Функция y = f (x) называется периодической, если существуеттакое число T, что f (x +T) = f (x).
Пример. Функция y = sin x является периодической, поскольку y
= sin x = sin(x +2 k). Период T = 2 .
Иванов О.В. Кудряшова Л.В. 2005
23
24. Обратная функция (inverse function)
Если для различных значений x значения функции y = f (x)различны, то для функции f можно рассмотреть обратную ей
функцию: x = f -1(y). Обратная функция означает установление
соответствия:
f -1
X
Y
Для обратной функции область определения – множество Y,
область значений - множество X.
Вопрос: всегда ли существует обратная функция?
Иванов О.В. Кудряшова Л.В. 2005
24
25. Примеры
1. Для функции y = sin x обратной функцией является x =arcsin y.
2. Для функции y = ax обратной функцией является x = loga y.
Иванов О.В. Кудряшова Л.В. 2005
25
26. 3. Элементарные функции
Пять видов основных элементарных функцийСложные функции
Общее понятие элементарной функции
Преобразование графиков
18 февраля 2024 г.
27. Основные элементарные функции
1. Степенная функция:2. Показательная функция:
3. Логарифмическая функция:
4. Тригонометрические функции:
y=x
y=ax
(a > 0, a 1)
y = log a x (a > 0, a 1)
y = sin x, y = cos x,
y = tg x, y = ctg x
5. Обратные тригонометрические функции:
y = arcsin x, y = arccos x,
y = arctg x, y = arcctg x
Иванов О.В. Кудряшова Л.В. 2005
27
28. Сложная функция
Пусть функция y = f (u) есть функция от переменной u,определенной на множестве U с областью значений Y, а
переменная u, в свою очередь, является функцией u = g (x) от
переменной x, определенной на множестве X, с областью
значений U. Тогда функция y = f(g(x)), заданная на множестве
X, называется сложной функцией.
f
g
X
U
Y
f(g(x))
Синонимы: композиция функций, суперпозиция функций, функция от функции.
Иванов О.В. Кудряшова Л.В. 2005
28
29. Понятие элементарной функции
Функции, построенные из основных элементарных функций спомощью конечного числа алгебраических действий и конечного
числа операций образования сложной функции, называются
элементарными.
Пример. Функция:
2x 3
y sin x
2
ln( x cos x 4)
является элементарной.
Иванов О.В. Кудряшова Л.В. 2005
29
30. Функция Дирихле
Пример неэлементарной функции - функция Дирихле:1, если x рационально
D( x )
0, если x иррационально
y
1
0
Иванов О.В. Кудряшова Л.В. 2005
x
Это не график, поскольку
построить график функции
Дирихле невозможно. Это
лишь ее схематическое
изображение!
30
31. Дирихле Петер Густав Лежён (1805 – 1859)
Дирихле (Dirichlet) Петер ГуставЛежён немецкий математик, член
Берлинской Академии наук. С 17
лет был домашним учителем в
Париже, в 22 года – доцент в
Бреславле, в 26 лет – профессор
Берлинского университета. С
1855
года
профессор
Геттингенского университета.
В математике задача, интеграл,
принцип, функция, ряды связаны
с именем Дирихле.
Иванов О.В. Кудряшова Л.В. 2005
31
32. Преобразование графиков
Если имеется функция y = f (x),то из ее графика путем преобразований можно получить график
функции y = A f (ax + b) + B,
где A, B, a, b – некоторые действительные числа.
Подробнее об этом в приложении к лекции.
Иванов О.В. Кудряшова Л.В. 2005
32
33. Пример сложной функции
Будон Р. Место беспорядка. Критика теории социальногоизменения. 1998.
Социальный или экономический феномен M является функцией
суммы действий m, зависящих от ситуации S, в которой
находятся акторы. Ситуация, в свою очередь, определяется
макросоциальными характеристиками M‘.
M M (m( S ( M )))
или
M MmSM
Иванов О.В. Кудряшова Л.В. 2005
33
34. 4. Последовательности
ПонятиеПримеры
18 февраля 2024 г.
35. Последовательность (sequence)
Числовой последовательностью{an} называется числовая функция:
an = f (n),
заданная
на
множестве
натуральных чисел n N.
Члены последовательности:
a 1 a2 a3 a4 … an …
Иванов О.В. Кудряшова Л.В. 2005
35
36. Примеры последовательностей
1. Последовательность:Общий член:
2. Последовательность:
Общий член:
Иванов О.В. Кудряшова Л.В. 2005
1 1 1 1
; ; ; ;...
2 3 4 5
1
an
n 1
- 3; 4; - 5; 6;...
an ( 1) n (n 2)
36
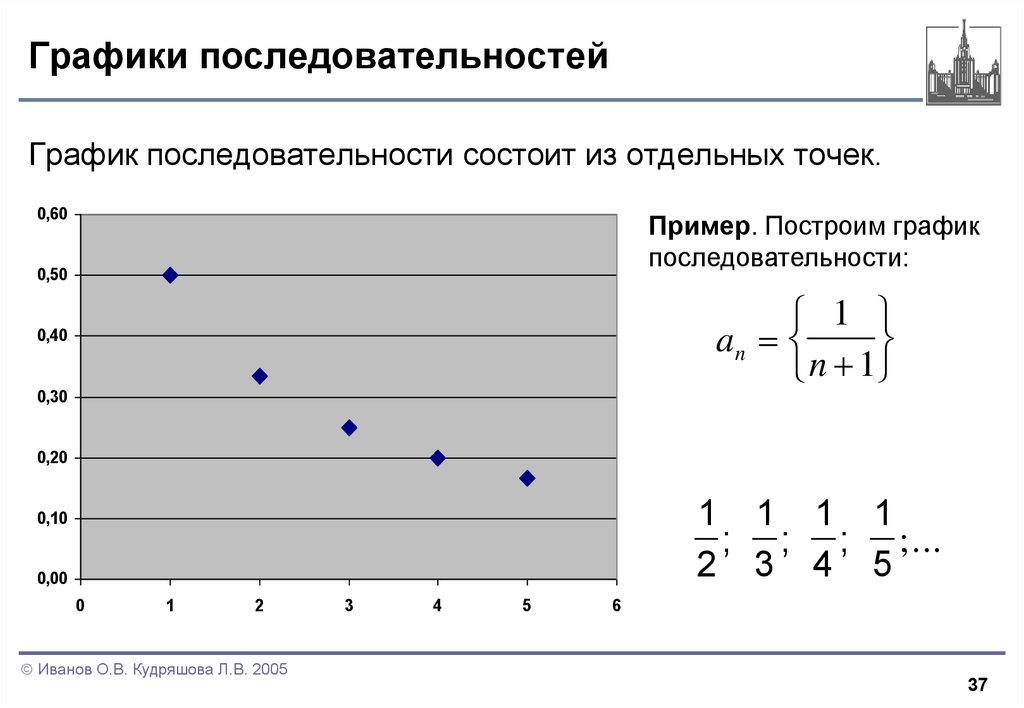
37. Графики последовательностей
График последовательности состоит из отдельных точек.0,60
Пример. Построим график
последовательности:
0,50
1
an
n 1
0,40
0,30
0,20
1 1 1 1
; ; ; ;...
2 3 4 5
0,10
0,00
0
1
2
Иванов О.В. Кудряшова Л.В. 2005
3
4
5
6
37
38. Графики последовательностей
Иногда точки соединяют сглаживающими линиями для удобстваи наглядности.
0,60
Пример. Построим график
последовательности:
0,40
0,20
0,00
0
1
2
3
-0,20
4
5
6
7
8
9
( 1) n
an
n
-0,40
-0,60
-0,80
-1,00
1
1 1
1
- 1; ; - ; ; - ;...
2
3 4
5
-1,20
Иванов О.В. Кудряшова Л.В. 2005
38
39. Ограниченная последовательность
Последовательность называется ограниченной, если найдетсятакое число такое положительное число M, что для любого
значения n выполняется условие | an | M.
Иванов О.В. Кудряшова Л.В. 2005
39
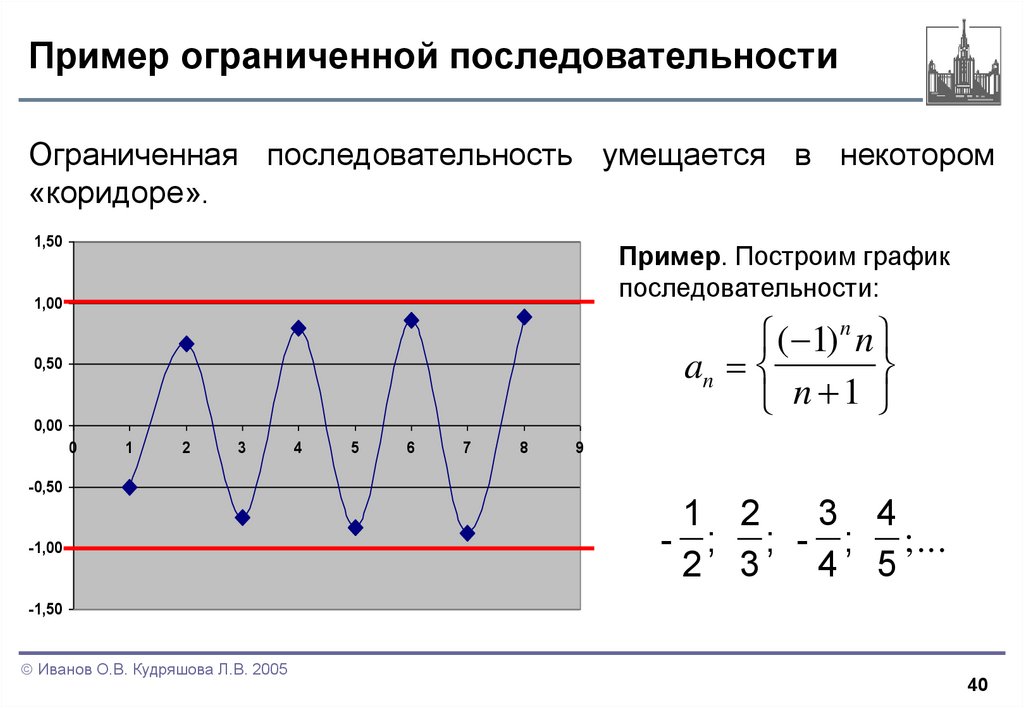
40. Пример ограниченной последовательности
Ограниченная последовательность умещается в некотором«коридоре».
1,50
Пример. Построим график
последовательности:
1,00
( 1) n n
an
n 1
0,50
0,00
0
1
2
3
-0,50
-1,00
4
5
6
7
8
9
1 2
3 4
- ; ; - ; ;...
2 3
4 5
-1,50
Иванов О.В. Кудряшова Л.В. 2005
40
41. Лекция Предел функции
1 Предел последовательности2 Предел функции
3 Бесконечно малые и бесконечно большие
4 Теоремы о пределах
5 Замечательные пределы
18 февраля 2024 г.
42. Эпиграф
Работайте, работайте, полное понимание придетпотOм.
Даламбер
Иванов О.В. Кудряшова Л.В. 2005
42
43. 1. Предел последовательности
Понятие последовательностиОпределение предела последовательности
Геометрический смысл
18 февраля 2024 г.
44. Последовательность
Числовой последовательностью{an} называется числовая функция:
an = f (n),
заданная
на
множестве
натуральных чисел n N.
Члены последовательности:
a 1 a2 a3 a4 … an …
Иванов О.В. Кудряшова Л.В. 2005
44
45. Предел числовой последовательности
Предел последовательности это число A, к которому членыпоследовательности
стремятся
при
неограниченном
возрастании номера n:
an A при n
Это нестрогое определение. Что такое «стремятся»?
Иванов О.В. Кудряшова Л.В. 2005
45
46. Предел числовой последовательности
Число А есть предел числовой последовательности {an}, еслидля любого, даже сколь угодно малого числа > 0 найдется
такой номер n0 (зависящий от ), что для всех членов
последовательности с номерами n > n0 будет выполнено
неравенство: | an – А |< (строгое определение).
Обозначение:
Иванов О.В. Кудряшова Л.В. 2005
lim an A
n
46
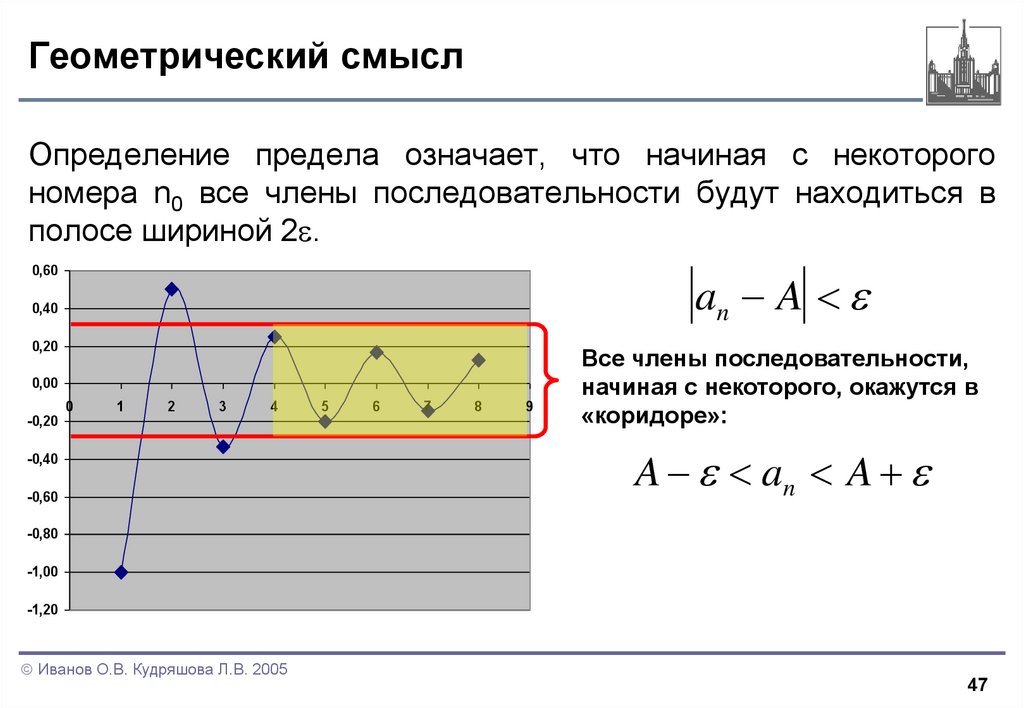
47. Геометрический смысл
Определение предела означает, что начиная с некоторогономера n0 все члены последовательности будут находиться в
полосе шириной 2 .
0,60
an A
0,40
0,20
0,00
0
1
2
3
4
-0,20
-0,40
-0,60
5
6
7
8
9
Все члены последовательности,
начиная с некоторого, окажутся в
«коридоре»:
A an A
-0,80
-1,00
-1,20
Иванов О.В. Кудряшова Л.В. 2005
47
48. Пример
Предел последовательностиравен 1.
3 4 5 6
101
1001
2; ; ; ; ;...;
;...;
;...
2 3 4 5
100
1000
Докажем это при помощи определения предела. Общий член
такой последовательности записывается в следующем виде:
n 1
1
an
1
n
n
Иванов О.В. Кудряшова Л.В. 2005
48
49. 2. Предел функции
Предел функции в бесконечностиПредел функции в точке
Геометрический смысл
18 февраля 2024 г.
50. Предел функции в бесконечности
Число А называется пределом функции y = f (x) при xстремящемся к бесконечности, если для любого, даже сколь
угодно малого положительного > 0, найдется такое число M
(зависящее от ), что для всех x таких, что |x|>M, выполнено
неравенство: | f (x) – A|< .
A lim f ( x) 0 M M ( ) x: x M : f ( x) A
x
Иванов О.В. Кудряшова Л.В. 2005
50
51. Предел функции в точке
Число А называется пределом функции y = f (x) при x a,если функция определена в некоторой окрестности точки a,
(кроме, может быть, самой точки a) и для любого, даже сколь
угодно малого положительного > 0, найдется такое число > 0
(зависящее от ), что для всех x из -окрестности точки a,
выполнено неравенство: | f (x) – A|< .
A lim f ( x) 0 ( ) 0: 0 x a f ( x) A
x a
Иванов О.В. Кудряшова Л.В. 2005
51
52. Геометрический смысл
Число А есть предел функции y = f (x) в точке a.Из того, что x окажется в -окрестности точки a, будет
следовать, что значение функции окажется в -окрестности
точки A.
y
y=f (x)
A+
A
A–
0
lim f ( x ) A
x a
a x a
a– a a+
Иванов О.В. Кудряшова Л.В. 2005
x
A f ( x) A
52
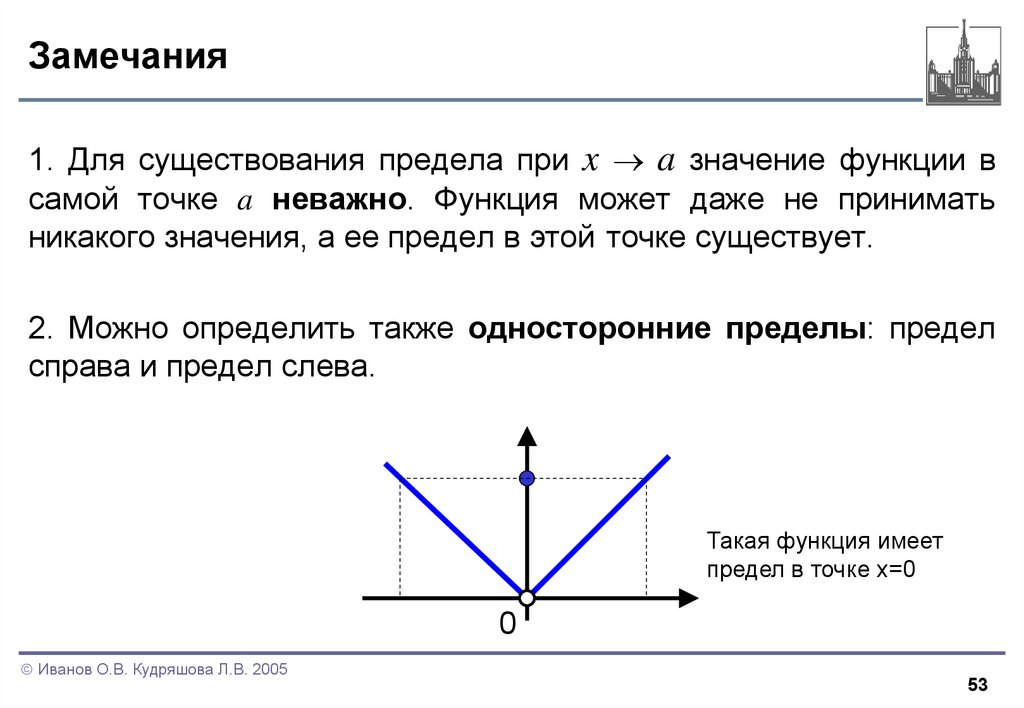
53. Замечания
1. Для существования предела при x a значение функции всамой точке a неважно. Функция может даже не принимать
никакого значения, а ее предел в этой точке существует.
2. Можно определить также односторонние пределы: предел
справа и предел слева.
Такая функция имеет
предел в точке x=0
0
Иванов О.В. Кудряшова Л.В. 2005
53
54. 3. Бесконечно малые и бесконечно большие величины
Определение и свойстваСвязь между бесконечно малыми и
бесконечно большими
18 февраля 2024 г.
55. Бесконечно малая величина
Функция (x) называется бесконечно малой величиной при xa (или при x ), если ее предел равен нулю:
lim ( x ) 0
x a
lim ( x) 0 0 ( ) 0: 0 x a ( x )
x a
Иванов О.В. Кудряшова Л.В. 2005
55
56. Пример
Функцияy x 3
является бесконечно малой при x 3.
В других точках эта функция бесконечно малой не является!
Иванов О.В. Кудряшова Л.В. 2005
56
57. Свойства бесконечно малых
Теорема 1. Сумма двух бесконечно малых есть бесконечномалая величина.
Теорема 2. Произведение бесконечно малой на ограниченную
функцию (в том числе на постоянную, на другую бесконечно
малую функцию) есть бесконечно малая.
Иванов О.В. Кудряшова Л.В. 2005
57
58. Бесконечно большие величины
Функция f (x) называется бесконечно большой величиной приx a (или при x ), если для любого, даже сколь угодно
большого числа M > 0 найдется (зависящее от M), что для всех
x таких, что 0 < | x – a |< , выполнено неравенство: | f (x)| > M.
lim f ( x )
x a
lim f ( x ) M 0 ( M ) 0: 0 x a f ( x ) M
x a
Иванов О.В. Кудряшова Л.В. 2005
58
59. Связь между б.м. и б.б.
Теорема 1. Если (x) – бесконечно малая, то 1/ (x) бесконечнобольшая.
Теорема 2. Если (x) – бесконечно большая, то 1/ (x)
бесконечно малая.
Доказательство можно найти в учебниках.
Иванов О.В. Кудряшова Л.В. 2005
59
60. Таблица эквивалентности
Если предел отношения двух бесконечно малых равен единице:( x)
lim
1
x a ( x )
то их называют эквивалентными при x a (или при x ):
( x) ( x)
Например,
sin ( x ) ( x )
В приложении приведена таблица эквивалентности некоторых
бесконечно малых величин.
Иванов О.В. Кудряшова Л.В. 2005
60
61. Таблица эквивалентности
Пусть (x) бесконечно малая функция при x 0.Тогда
tg ( x) ~ ( x)
(1 ( x)) 1 ~ p ( x)
( x)
sin ( x ) ~ ( x )
a
1 ~ ( x) ln a
ln(1 ( x )) ~ ( x )
arcsin ( x ) ~ ( x )
2
1 cos ( x) ~ ( ( x)) / 2 arctg ( x) ~ ( x)
p
Иванов О.В. Кудряшова Л.В. 2005
61
62. 4. Основные теоремы о пределах
Единственность пределаПредел суммы, произведения, частного
Признаки существования предела
18 февраля 2024 г.
63. Основные теоремы о пределах
Рассмотрим теоремы, которые облегчают нахождение пределовфункций.
x или
x0
x аналогичны,
Формулировка теорем, когда
поэтому
будем пользоваться обозначением:
. lim f ( x )
Предел суммы (разности) двух функций равен сумме (разности)
пределов:
lim f1( x ) f2 ( x ) lim f1( x ) lim f2 ( x )
Предел произведения двух функций равен произведению пределов:
lim f1( x ) f2 ( x ) lim f1( x ) lim f2 ( x )
Постоянный множитель можно выносить за знак предела:
lim C f ( x ) C lim f ( x )
Иванов О.В. Кудряшова Л.В. 2005
63
64. Основные теоремы о пределах
Предел дроби равен пределу числителя, деленному на пределзнаменателя, если предел знаменателя не равен нулю:
f1( x ) lim f1( x )
lim
f2 ( x ) lim f2 ( x )
lim f ( x ) 0
2
Предел степени с натуральным показателем равен той же степени
предела:
lim f ( x ) lim f ( x )
n
n
Предел показательно – степенной функции:
lim f ( x )
g(x)
Иванов О.В. Кудряшова Л.В. 2005
lim f ( x )
lim g ( x )
64
65. 5. Замечательные пределы
Первый замечательный пределВторой замечательный предел
18 февраля 2024 г.
66. Первый замечательный предел
sin xlim
1
x 0
x
Это означает, что синус малого угла есть бесконечно малая того
же порядка, что и сам угол.
Иванов О.В. Кудряшова Л.В. 2005
66
67. Второй замечательный предел
Числом e (вторым замечательным пределом) называетсяпредел числовой последовательности:
n
1
lim 1 e
n
n
Это пример
ограничена.
последовательности,
Иванов О.В. Кудряшова Л.В. 2005
которая
монотонная
и
67
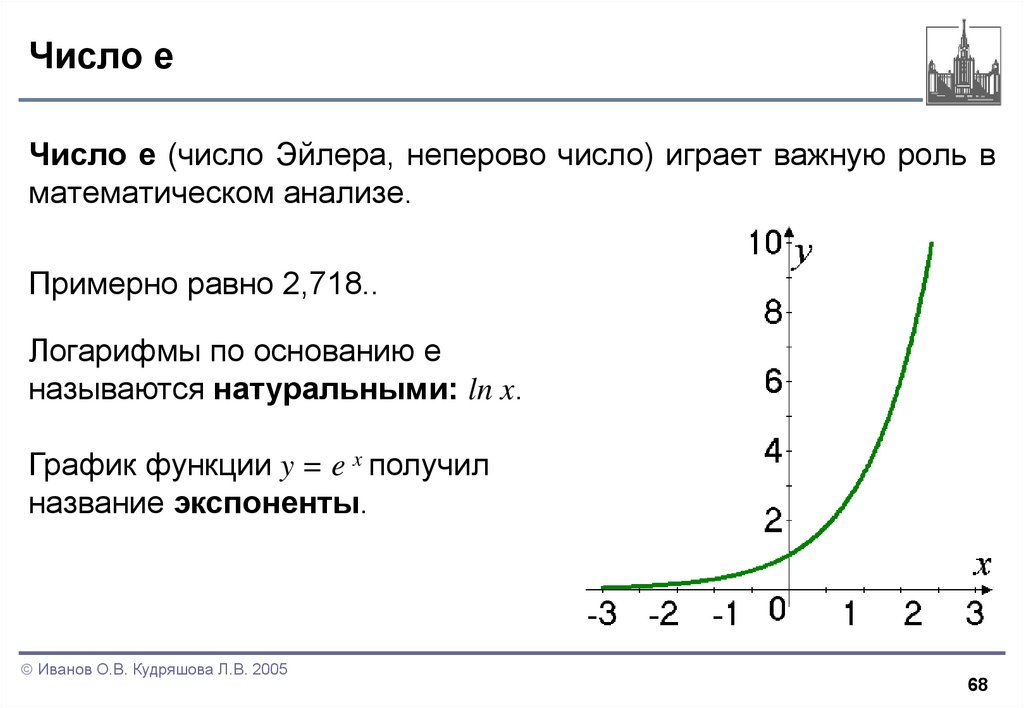
68. Число е
Число е (число Эйлера, неперово число) играет важную роль вматематическом анализе.
Примерно равно 2,718..
Логарифмы по основанию е
называются натуральными: ln x.
График функции y = e x получил
название экспоненты.
Иванов О.В. Кудряшова Л.В. 2005
68
69. Решение задач
18 февраля 2024 г.70. Вычисление пределов
Непосредственное вычисление пределаРаскрытие неопределенностей вида 0/0
Раскрытие неопределенностей вида /
Раскрытие неопределенностей вида – и 0
Раскрытие неопределенностей вида 1 , 0 и 00
Иванов О.В. Кудряшова Л.В. 2005
70
71. Вычислить пределы:
lim ( x 7 x 4) 3 7 3 4 8;2
2
x 3
x 4
( x 2)( x 2)
x 2
lim 2
lim
lim
2;
x 2 x 2 x
x 2
x 2 x
x( x 2)
3
2
(
x
2
)(
x
)
2
( 0 / 0)
2x 7x 6
2x 3
2
lim
lim
lim
;
2
x 2 ( x 2) 2
x 2
x 2 x 2
( x 2)
2
Иванов О.В. Кудряшова Л.В. 2005
71
72.
Вычислить пределы:2 x 3x 5 x 7
lim
3
2
x 3 x 4 x x 2
3
2
2x
3x
5x 7
3
3
3
3
2
x
x
x
x
lim
x
4 1
2
3
3 2 3
x x
x
3
Иванов О.В. Кудряшова Л.В. 2005
2
( / )
72
73. Вычислить пределы:
..
.
.
.
..
3x 2 4 x 2
lim 2
x x 6 x 5
2 x 2 5x
lim
x 3 x 3 5 x 1
x2 1
lim 2
x 1 x 6 x 7
x
lim
x 0 sin 5 x
ctg 2 x
5x
x
2
1 x
lim (1 )
x 2
x
sin 6 x
x 0
5x
lim
x 3
lim
x
x
2
lim
x 0
Иванов О.В. Кудряшова Л.В. 2005
1
x
2 3
lim 1
x
x
lim
x
1 cos 6 x
4x 2
73






























































 Математика
Математика








