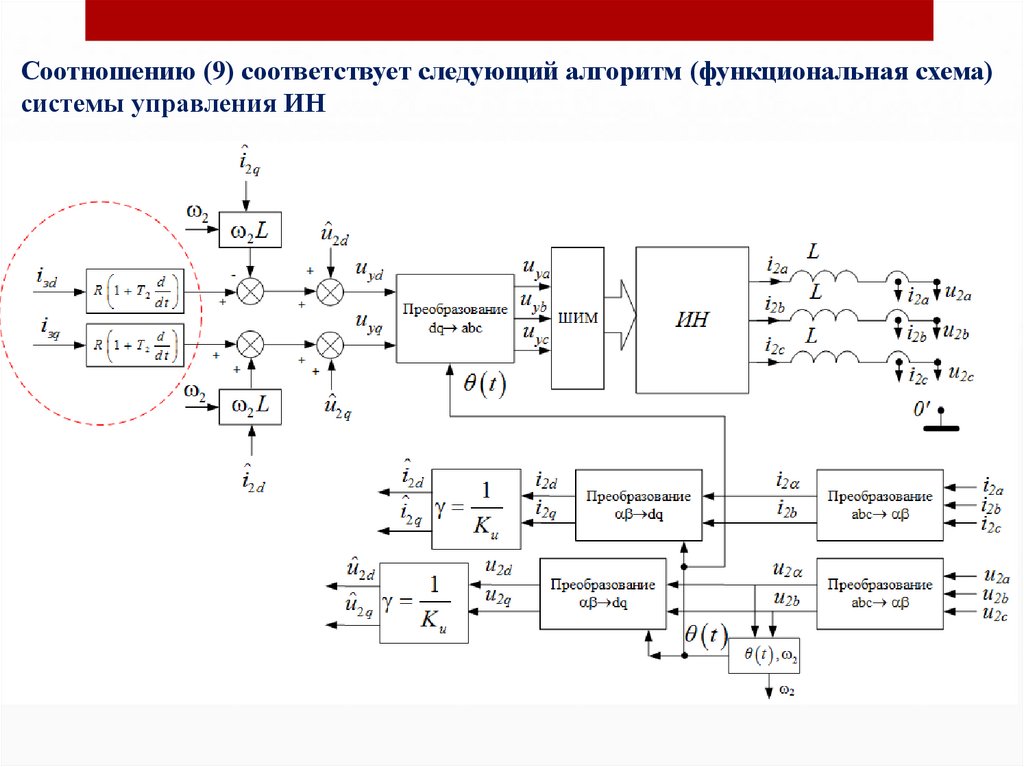
Похожие презентации:
Лекция_7_Векторное_управление_ИН
1.
2.
Векторные алгоритмы – это такие алгоритмы в которыхсигналы на ШИМ формируются с использованием
результирующего (описывающего) вектора.
При построении системы регулирования выходного тока и
напряжения также используется результирующий вектор
сигналов управления.
Проиллюстрируем, в качестве примера, синтез векторного
алгоритма управления ИН как источником тока во
вращающейся («dq») системе координат.
3.
Задача: превратить ИН в источник тока, т.е. выходной токинвертора должен завесить только от сигнала задания.
k- константа.
i2 k iз
Где необходимо такое управление, например:
- электропривод переменного тока (I ~ момент);
- индукционный нагрев (I ~ температура);
- в научном приборостроении (I ~ напряженность магнитного
поля );
- активный фильтр.
Как можно этого добиться?
ИН по природе источник напряжения, сделать источник тока
можно с помощью обратной связи.
4.
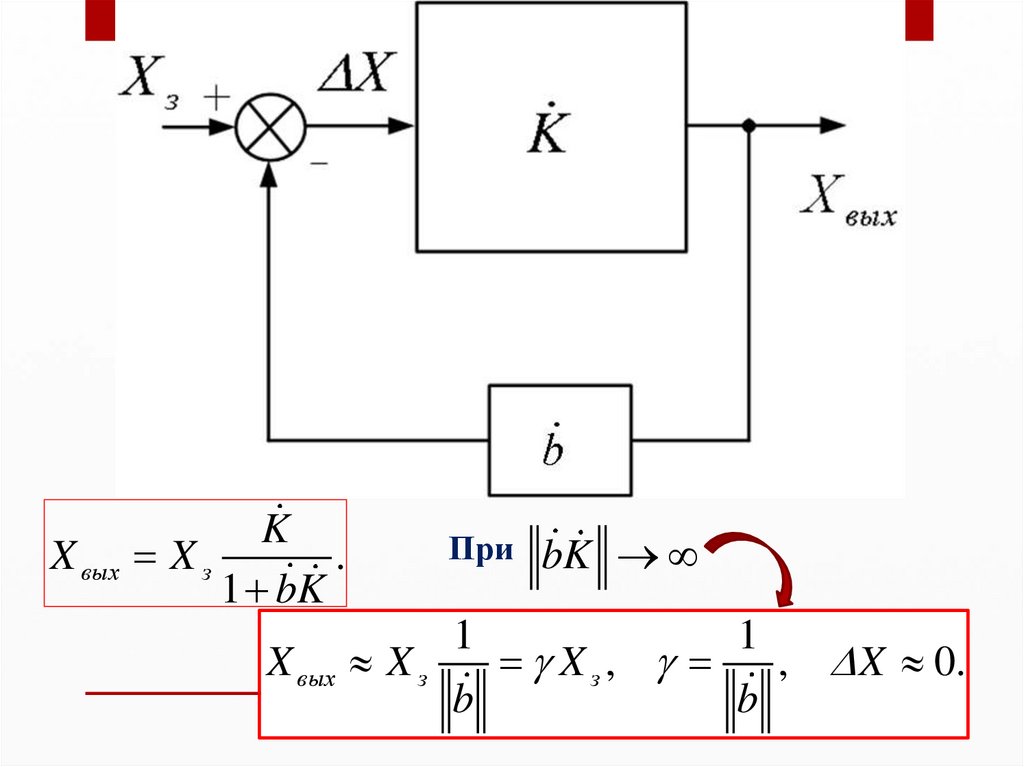
KX вых X з
.
1 bK
При
bK
1
1
X вых X з
Xз,
, X 0.
b
b
5.
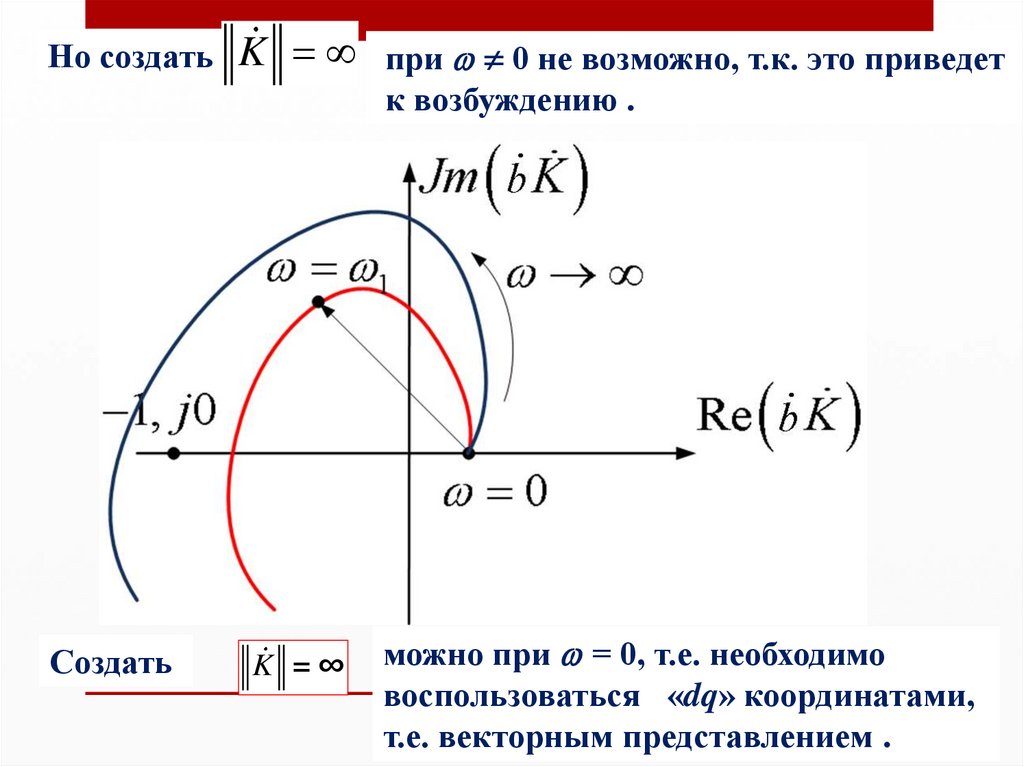
Но создатьK при 0 не возможно, т.к. это приведет
к возбуждению .
Создать
K =∞
можно при = 0, т.е. необходимо
воспользоваться «dq» координатами,
т.е. векторным представлением .
6.
Синтез алгоритма начинается сполучения
математической модели ИН во
вращающейся системе координат.
13.11.2021г.
7.
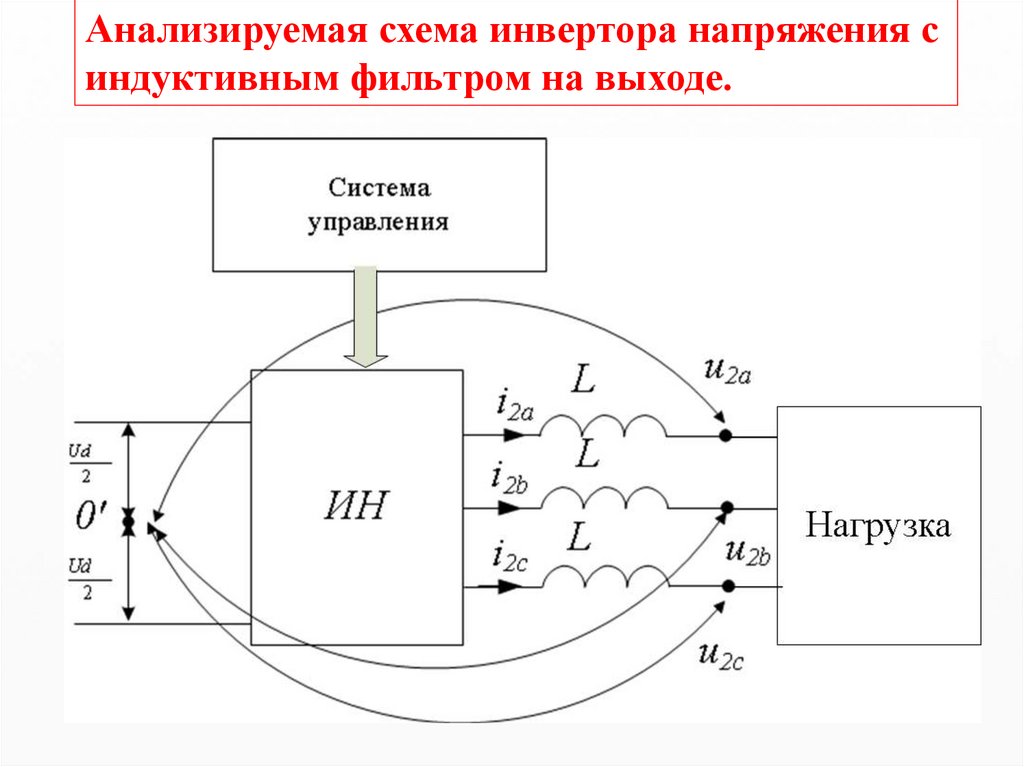
Анализируемая схема инвертора напряжения синдуктивным фильтром на выходе.
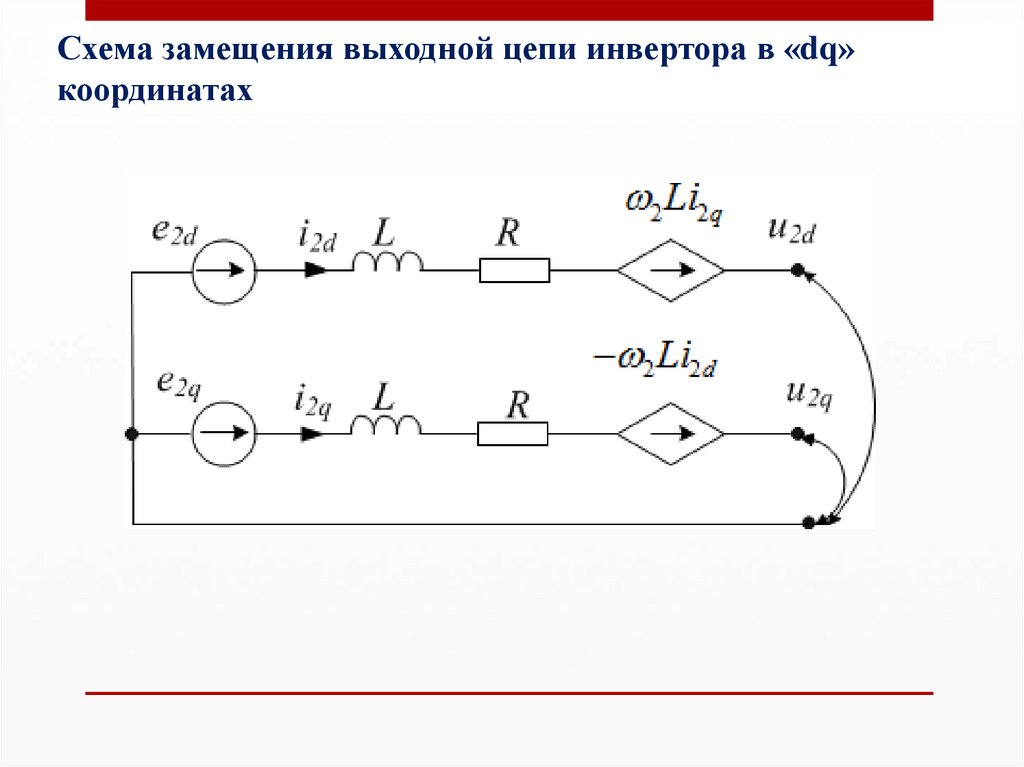
8.
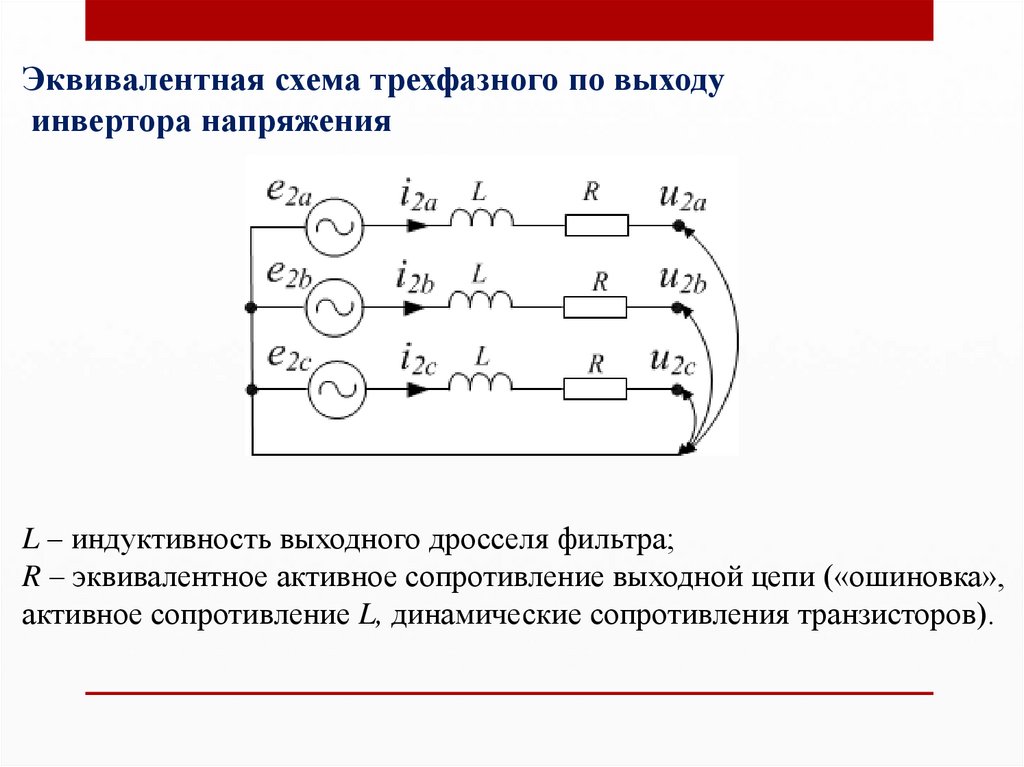
Эквивалентная схема трехфазного по выходуинвертора напряжения
L – индуктивность выходного дросселя фильтра;
R – эквивалентное активное сопротивление выходной цепи («ошиновка»,
активное сопротивление L, динамические сопротивления транзисторов).
9.
10.
11.
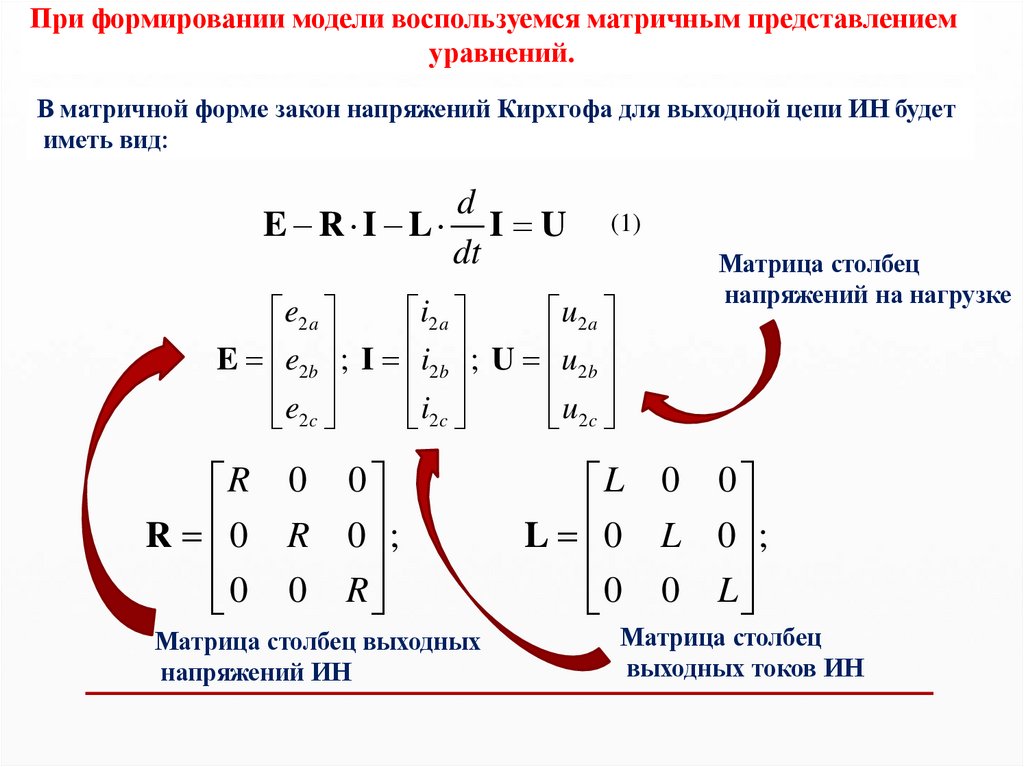
При формировании модели воспользуемся матричным представлениемуравнений.
В матричной форме закон напряжений Кирхгофа для выходной цепи ИН будет
иметь вид:
d
E R I L I U
dt
(1)
e2 a
i2 a
u2 a
E e2b ; I i2b ; U u2b
e2 c
i2 c
u2 c
R 0 0
R 0 R 0 ;
0 0 R
Матрица столбец выходных
напряжений ИН
Матрица столбец
напряжений на нагрузке
L 0 0
L 0 L 0 ;
0 0 L
Матрица столбец
выходных токов ИН
12. Переход из трехфазной системы «авс» координат во вращающуюся ортогональную систему «dq» координат.
Переход осуществляется в пошагово:1. переход в неподвижную ортогональную систему « 0»
координат («0» появляется, если есть в токах и
напряжениях нулевая последовательность, если её нет, то
просто « » координаты);
2. определение зависимости от времени угла поворота (t)
результирующих векторов токов и напряжений;
3. переход из неподвижной ортогональной системы « »
координат во вращающуюся с частотой d (t)/dt
ортогональную систему «dq» координат.
13.
Напомним, что переход в « 0» координаты, одновременно с выделениемнулевой последовательности (e0), например, в выходном напряжении ИН
осуществляется с помощью следующих соотношений:
1
2
e0
2
e
1
3
e
0
1
2
1
2
3
2
1
2 e
a
1
eb ;
2
ec
3
2
e 0 T 0 eabc ;
1
2
2
T 0
1
3
0
1
2
1
2
3
2
1
2
1
2
3
2
Матрица преобразования
из
«abc» координат в « 0»
координаты
Данный вид матрицы
преобразования
обеспечивает равенство
активной мощности в «abc» и
« 0» координатах!
14.
Обратный переход из « 0» координат в «abc» координаты,необходим, если используется далее скалярная ШИМ:
1
2
ea
e 2 1
b
3 2
ec
1
2
1
1
2
1
2
0
e0
3
e ;
2
e
3
2
e abc T 0 e 0 ; T 0 = T 0 ; T 0 Tαβ0 1 – единичная матрица;
1
1
2
2 1
T 0
3 2
1
2
1
1
2
1
2
0
3
2
3
2
Матрица преобразования из
« 0» координат в «abc» координаты
15.
Применяем преобразование Т β0 к матричному уравнению (1), для этогоумножим слева на право это уравнение на матрицу Т β0
d
T 0 E T 0 R T 0T 0 I T 0 L T 0 T 0 I T 0 U;
dt
1
1
Вставка этих произведений не нарушает тождества
(Т β0 не зависит от времени, поэтому можно внести под знак производной).
Если в напряжениях e2j нет нулевой последовательности, то в векторах
столбцах можно вычеркнуть верхнюю строчку, а в квадратных матрицах
вычеркивается первая строка или первый столбец (в этом случае получим
координаты « »).
1
1
2
2
T
3
3
0 2
1
2
3
2
1
2 1
T
3 2
1
2
0
3
2
3
2
16.
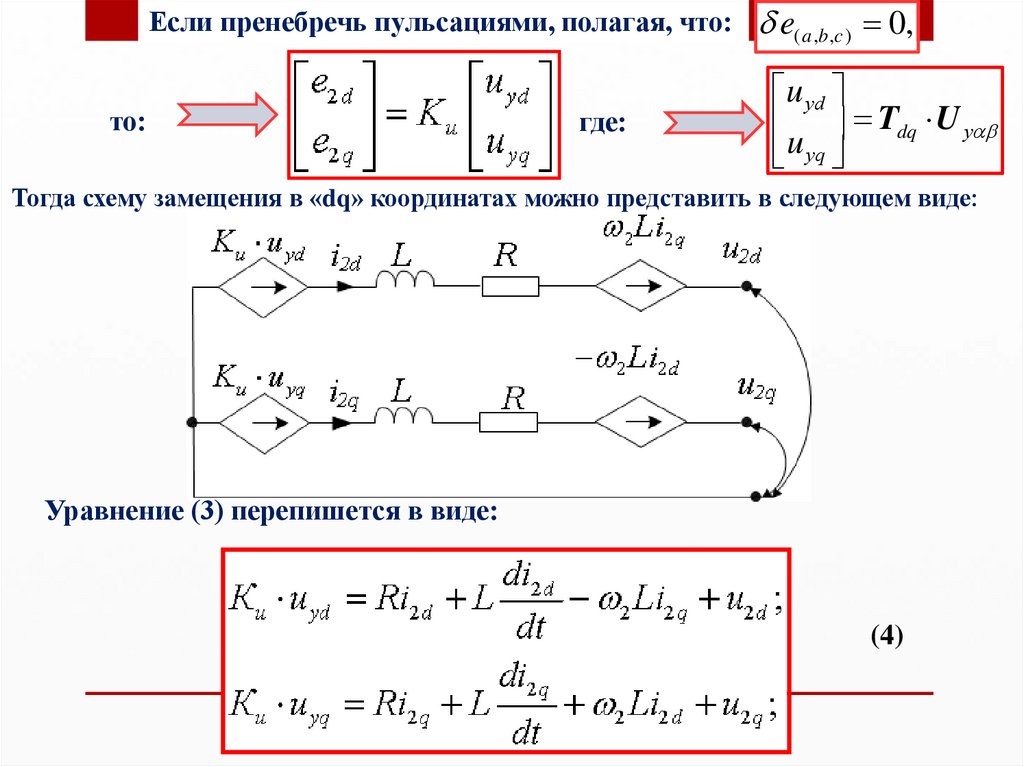
Предположим, что в нашем случае это имеет место, тогда:17.
В матричной форме закон напряжений Кирхгофа для выходной цепи ИН в « »координатах будет иметь вид:
(2)
В матричной форме сигналы управления ИН в « » координатах определятся
следующим образом:
Для переход из « » координат во вращающуюся систему
координат «dq» необходимо определить её частоту вращения,
которая задается сигналами управления:
t , 2 -
зависимость от времени угла поворота и частота вращения
результирующего вектора сигналов управления.
18.
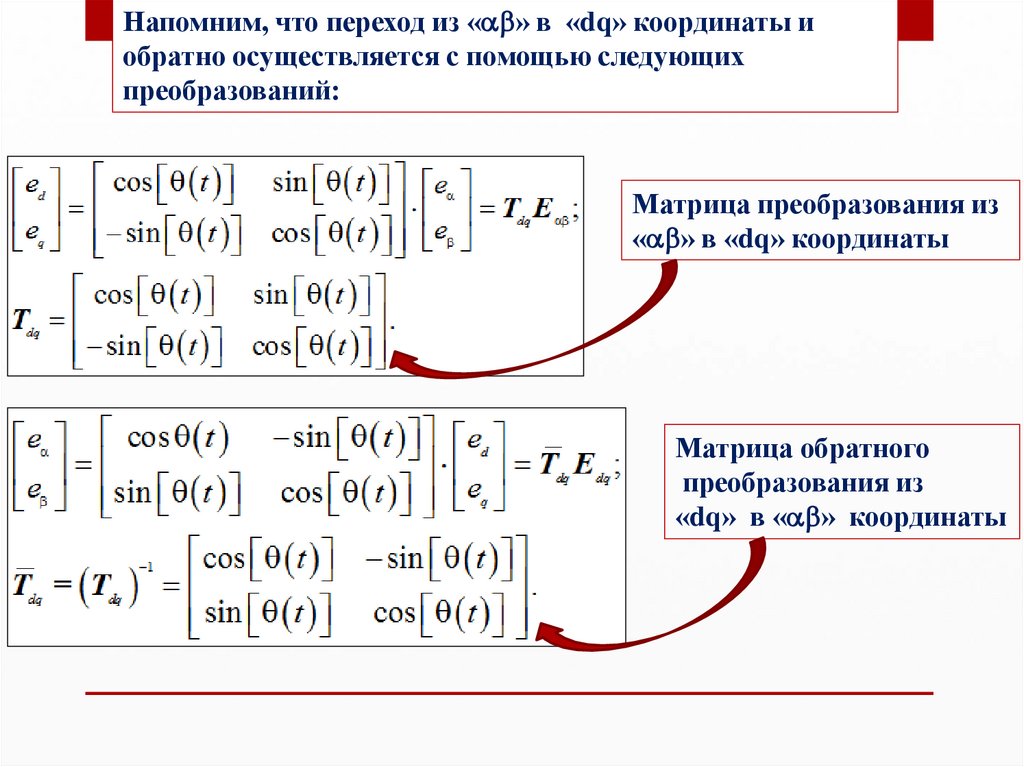
Напомним, что переход из « » в «dq» координаты иобратно осуществляется с помощью следующих
преобразований:
Матрица преобразования из
« » в «dq» координаты
Матрица обратного
преобразования из
«dq» в « » координаты
19.
Переведем систему уравнений (2) во вращающуюся систему координат«dq», для этого умножим слева на право уравнение (2) на матрицу Тdq
Вставка этих произведений
не нарушает тождества
e2 d
Edq Tdq E ; Edq
e2 q
20.
не нарушает тождестваcos[ (t )] sin[ (t )]
sin[ (t )] – cos[ (t )]
d
Tdq Tdq
2
dt
– sin[ (t )] cos[ (t )]
cos[ (t )] sin[ (t )]
0 1
2
W;
1 0
ഥ