Похожие презентации:
Электрические заряды. Закон сохранения электрического заряда. Закон Кулона. Напряженность поля
1. ЭЛЕКТРОСТАТИКА
раздел физики,в котором рассматриваются свойства и взаимодействия
неподвижных
в ИСО электрически заряженных тел
2.
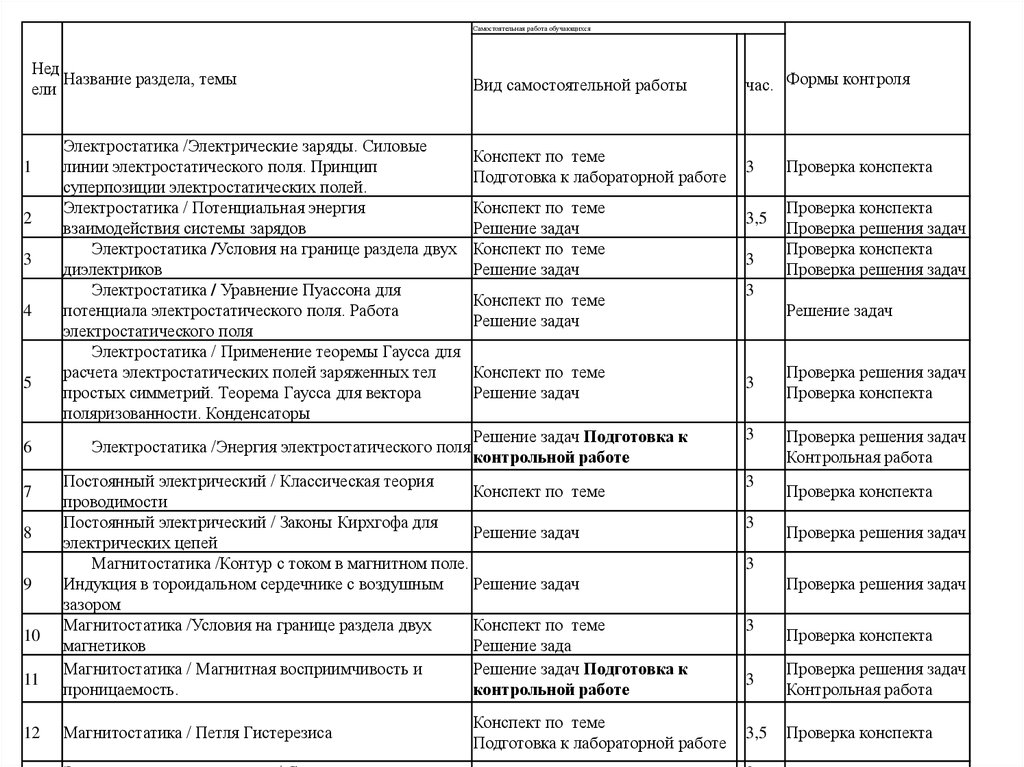
Самостоятельная работа обучающихсяНед
Название раздела, темы
ели
1
2
3
4
5
6
7
8
9
10
11
12
Электростатика /Электрические заряды. Силовые
линии электростатического поля. Принцип
суперпозиции электростатических полей.
Электростатика / Потенциальная энергия
взаимодействия системы зарядов
Электростатика /Условия на границе раздела двух
диэлектриков
Электростатика / Уравнение Пуассона для
потенциала электростатического поля. Работа
электростатического поля
Электростатика / Применение теоремы Гаусса для
расчета электростатических полей заряженных тел
простых симметрий. Теорема Гаусса для вектора
поляризованности. Конденсаторы
Вид самостоятельной работы
час. Формы контроля
Конспект по теме
Подготовка к лабораторной работе
3
Конспект по теме
Решение задач
Конспект по теме
Решение задач
Конспект по теме
Решение задач
Конспект по теме
Решение задач
3,5
3
Проверка конспекта
Проверка конспекта
Проверка решения задач
Проверка конспекта
Проверка решения задач
3
Решение задач
3
Проверка решения задач
Проверка конспекта
Решение задач Подготовка к
контрольной работе
3
Проверка решения задач
Контрольная работа
Постоянный электрический / Классическая теория
Конспект по теме
проводимости
Постоянный электрический / Законы Кирхгофа для
Решение задач
электрических цепей
Магнитостатика /Контур с током в магнитном поле.
Индукция в тороидальном сердечнике с воздушным
Решение задач
зазором
Магнитостатика /Условия на границе раздела двух
Конспект по теме
магнетиков
Решение зада
Магнитостатика / Магнитная восприимчивость и
Решение задач Подготовка к
проницаемость.
контрольной работе
3
Проверка конспекта
3
Проверка решения задач
Электростатика /Энергия электростатического поля
Магнитостатика / Петля Гистерезиса
Конспект по теме
Подготовка к лабораторной работе
3
Проверка решения задач
3
Проверка конспекта
3
Проверка решения задач
Контрольная работа
3,5
Проверка конспекта
3.
1.Электрические заряды.
Закон сохранения электрического заряда.
2. Закон Кулона.
3. Электростатическое поле. Напряжённость поля.
4. Примеры вычисления напряжённости поля.
.
3
4.
1. Электрические заряды.Закон сохранения
электрического заряда.
q
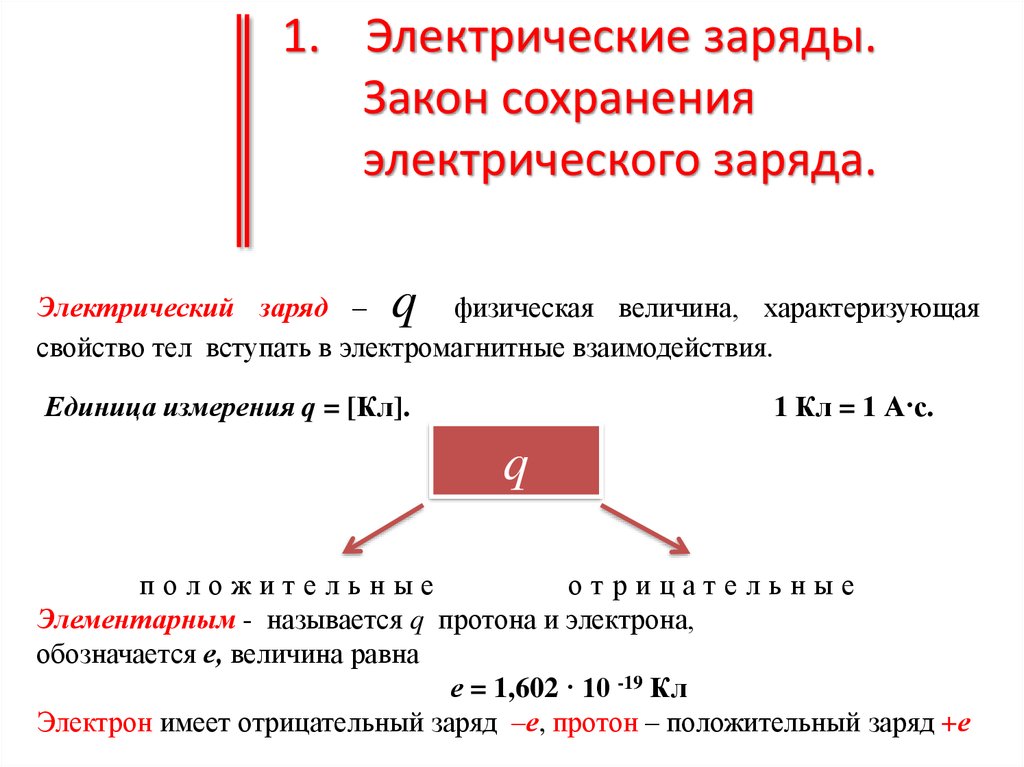
Электрический заряд –
физическая величина, характеризующая
свойство тел вступать в электромагнитные взаимодействия.
Единица измерения q = [Кл].
1 Кл = 1 А·с.
q
положительные
отрицательные
Элементарным - называется q протона и электрона,
обозначается е, величина равна
е = 1,602 · 10 -19 Кл
Электрон имеет отрицательный заряд –е, протон – положительный заряд +е
5.
Надо знать!- Электрически нейтральные системы содержат равное
число зарядов противоположного знака.
- Для электризации тела необходимо создать на
нем избыток зарядов того или иного знака.
- Закон сохранения заряда:
алгебраическая сумма зарядов в замкнутой
системе сохраняется.
6.
7.
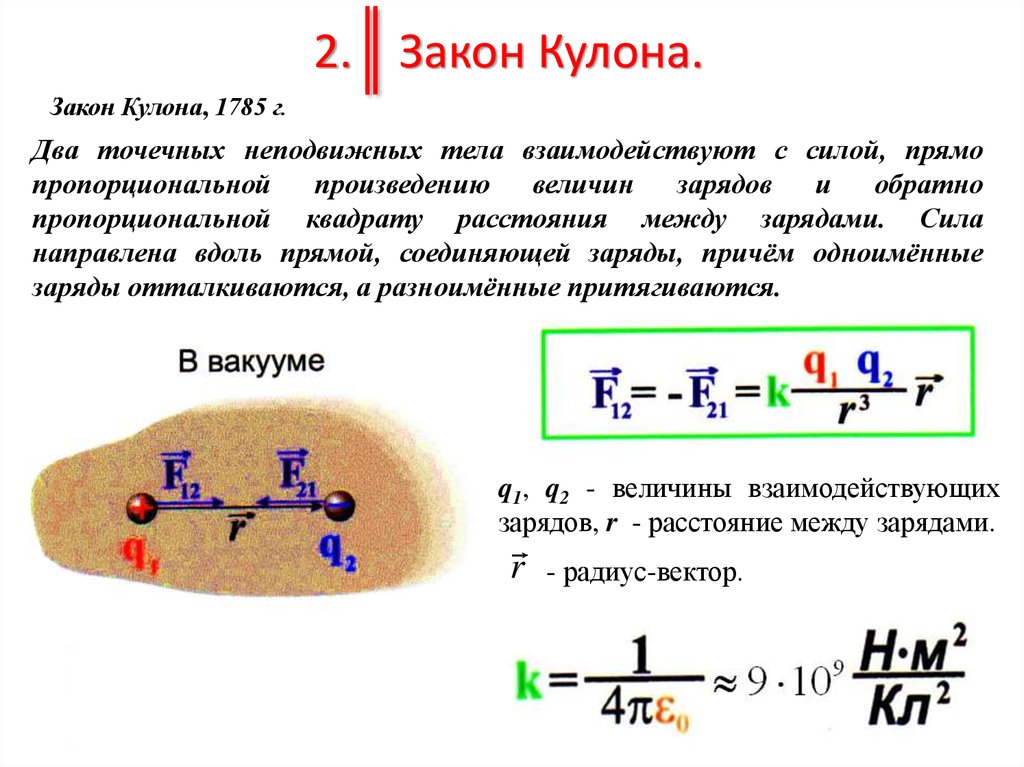
2. Закон Кулона.Закон Кулона, 1785 г.
Два точечных неподвижных тела взаимодействуют с силой, прямо
пропорциональной
произведению
величин
зарядов
и
обратно
пропорциональной квадрату расстояния между зарядами. Сила
направлена вдоль прямой, соединяющей заряды, причём одноимённые
заряды отталкиваются, а разноимённые притягиваются.
q1, q2 - величины взаимодействующих
зарядов, r - расстояние между зарядами.
r
- радиус-вектор.
8.
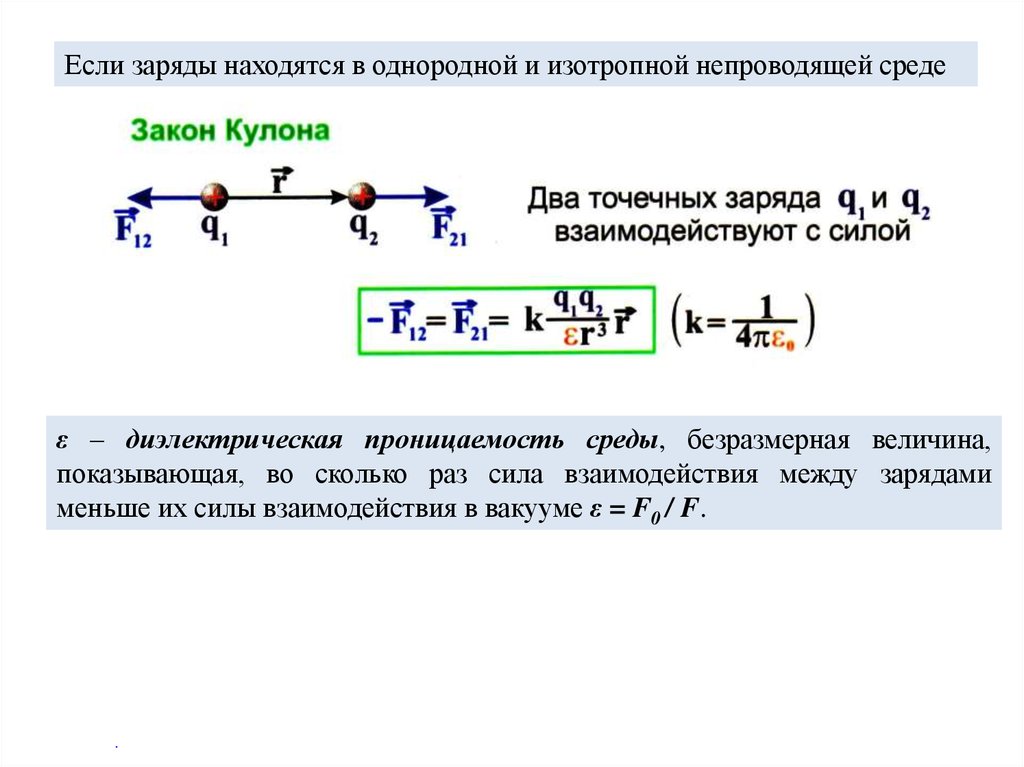
Если заряды находятся в однородной и изотропной непроводящей средеε – диэлектрическая проницаемость среды, безразмерная величина,
показывающая, во сколько раз сила взаимодействия между зарядами
меньше их силы взаимодействия в вакууме ε = F0 / F.
9.
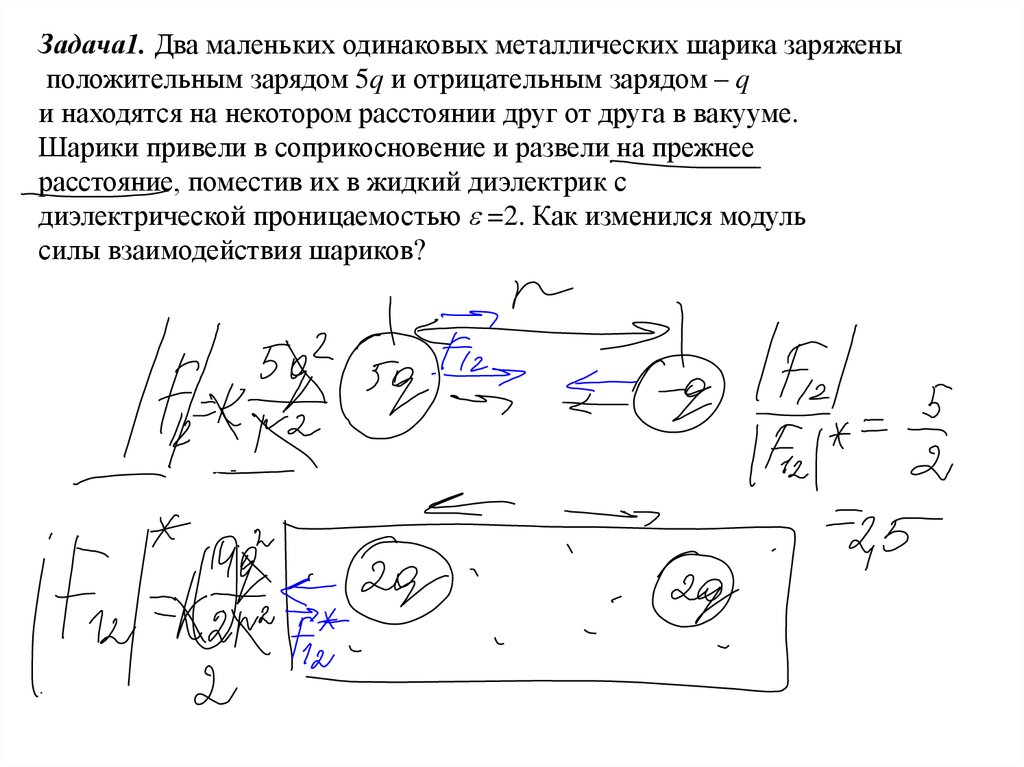
Задача1. Два маленьких одинаковых металлических шарика заряженыположительным зарядом 5q и отрицательным зарядом – q
и находятся на некотором расстоянии друг от друга в вакууме.
Шарики привели в соприкосновение и развели на прежнее
расстояние, поместив их в жидкий диэлектрик с
диэлектрической проницаемостью =2. Как изменился модуль
силы взаимодействия шариков?
10.
Задача 2. Два металлических шарика одинакового радиуса и массы подвешены водной точке на нитях одинаковой длины так, что их поверхности соприкасаются.
Какой заряд Q нужно сообщить шарикам, чтобы сила натяжения нитей стала
равной T=98 мН? Расстояние от центра шарика до точки подвеса равно l=10 см,
масса каждого шарика m=5 г.
Решение
Дано
T = 98 мН
l = 10 см
m= 5 г
Q-?
Fk T
mg
Ответ: Q=1,1 мкКл.
11.
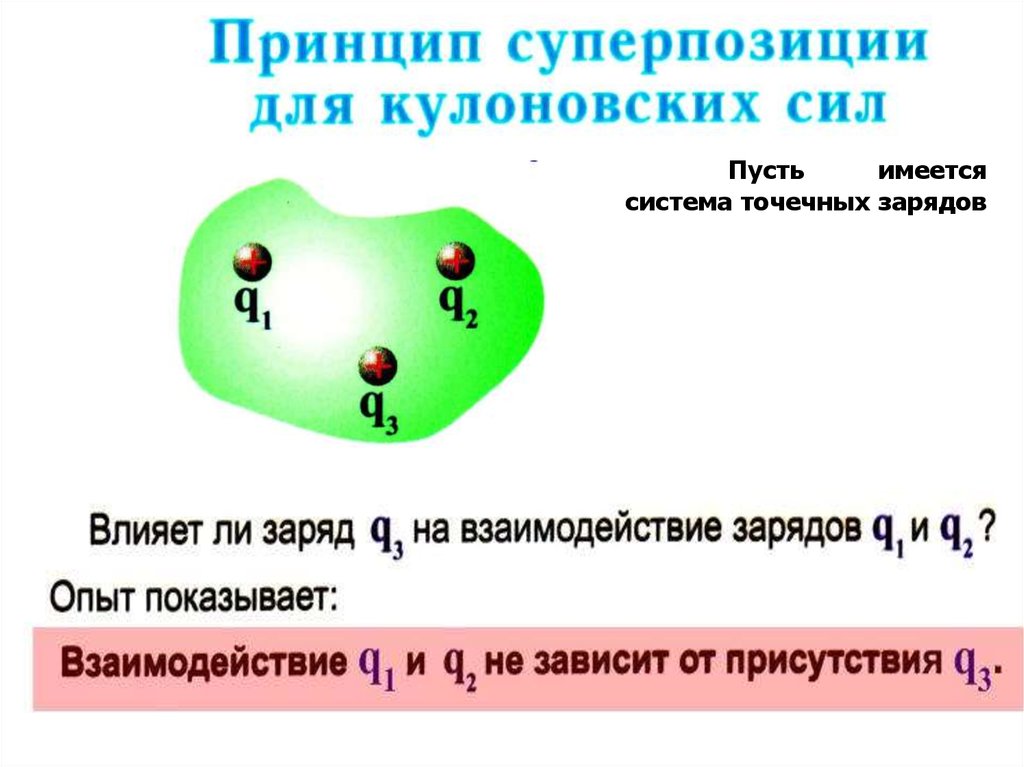
Пустьимеется
система точечных зарядов
12.
313.
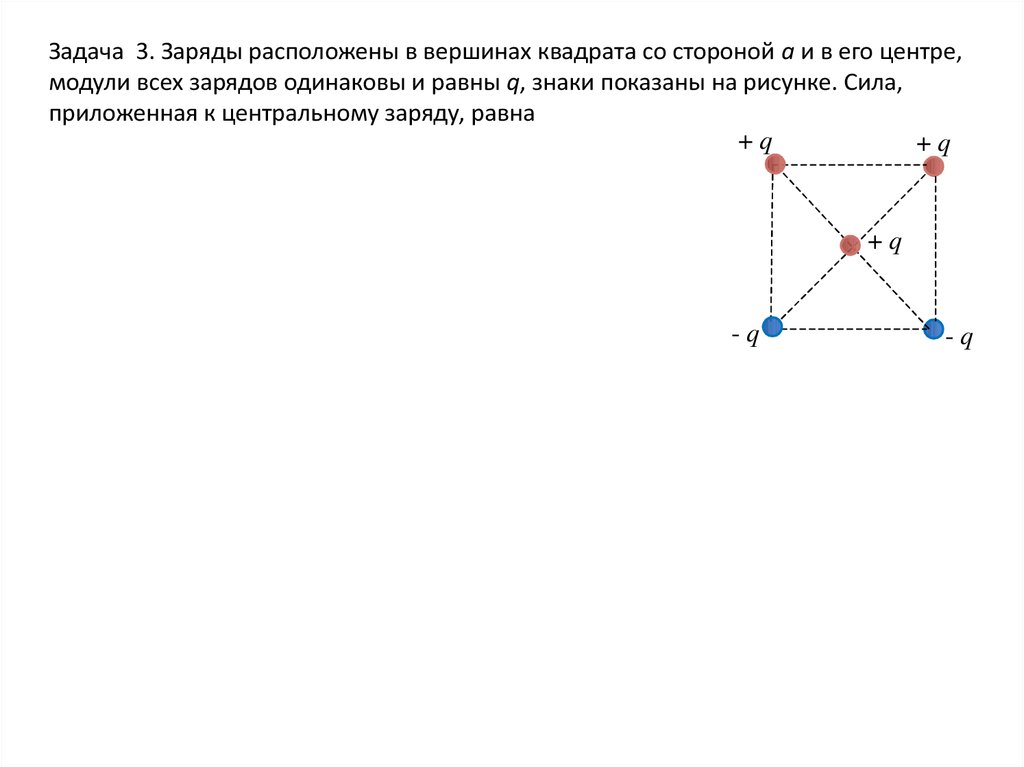
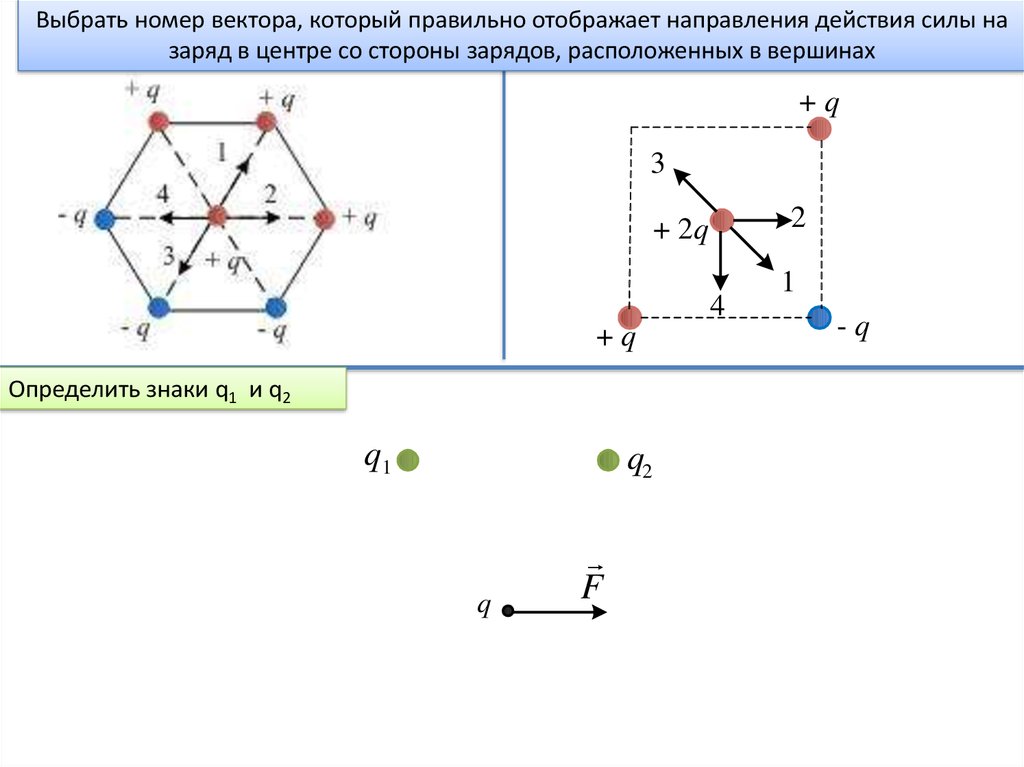
Задача 3. Заряды расположены в вершинах квадрата со стороной а и в его центре,модули всех зарядов одинаковы и равны q, знаки показаны на рисунке. Сила,
приложенная к центральному заряду, равна
+q
+q
+q
-q
-q
14.
Выбрать номер вектора, который правильно отображает направления действия силы назаряд в центре со стороны зарядов, расположенных в вершинах
+q
3
2
+ 2q
4
+q
Определить знаки q1 и q2
q1
q2
q
F
1
-q
15.
3. Электростатическое поле.Напряжённость поля.
Силовое поле – протяжённый материальный объект,
занимающий какую-либо часть пространства,
в каждой точке которой на некоторые тела действуют
вполне определённые силы.
Различные физические поля отличаются друг от друга по следующим
признакам:
1) в результате наличия каких тел и в каких условиях то или иное поле
возникает;
2) на какие тела (и в каких условиях) то или иное поле действует;
3) каковы силы, действующие на те или иные тела.
Например, гравитационное поле
1) возникает, если имеются тела, обладающие массой;
2) действует на тела, обладающие массой;
3) сила, действующая со стороны гравитационного поля на тела,
обладающие массой в конечном счёте определяется
законом всемирного тяготения.
16.
Стационарное поле – такое поле, в котором сила зависит только откоординат, но не зависит от времени.
Электрический заряд – особое свойство материального объекта, которое
проявляется в наличии в окружающем пространстве связанного с этим
объектом электромагнитного поля.
Пробный заряд не искажает исследуемое поле (не
перераспределения зарядов, создающих электрическое поле).
вызывает
17.
Таким образом, стационарное электрическое поле1) возникает, если имеются тела, обладающие электрическим зарядом;
2) действует на тела, обладающие электрическим зарядом;
3) сила, действующая со стороны стационарного электрического поля на
тела, обладающие зарядом, в конечном счёте определяется законом
Кулона и принципом суперпозиции.
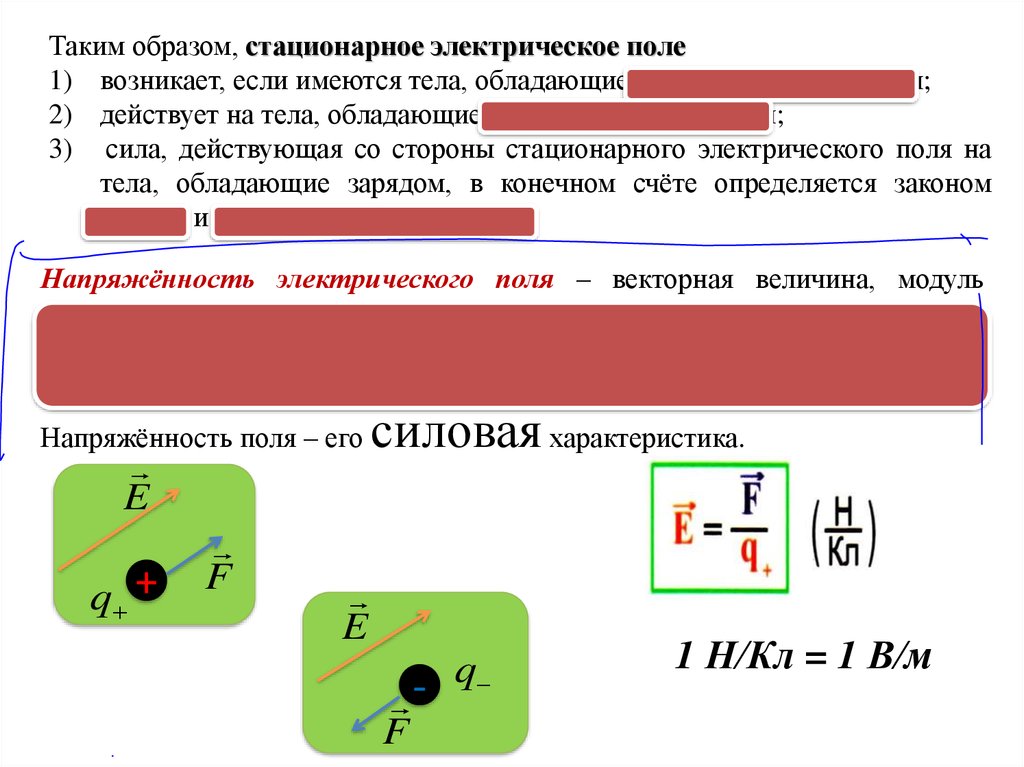
Напряжённость электрического поля – векторная величина, модуль
которой равен силе, действующей на единичный точечный положительный
заряд, помещённый в данную точку поля, а направление совпадает с
направлением силы, действующей на положительный заряд.
Напряжённость поля – его
E
q +
F
силовая характеристика.
E
q
F
1 Н/Кл = 1 В/м
18.
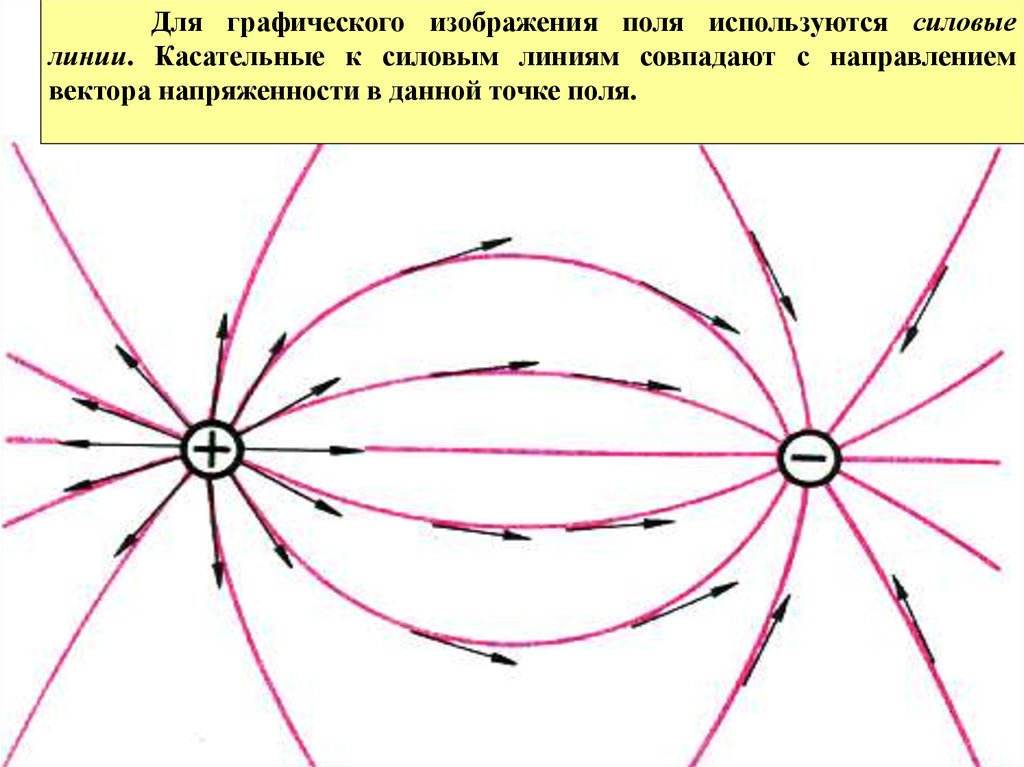
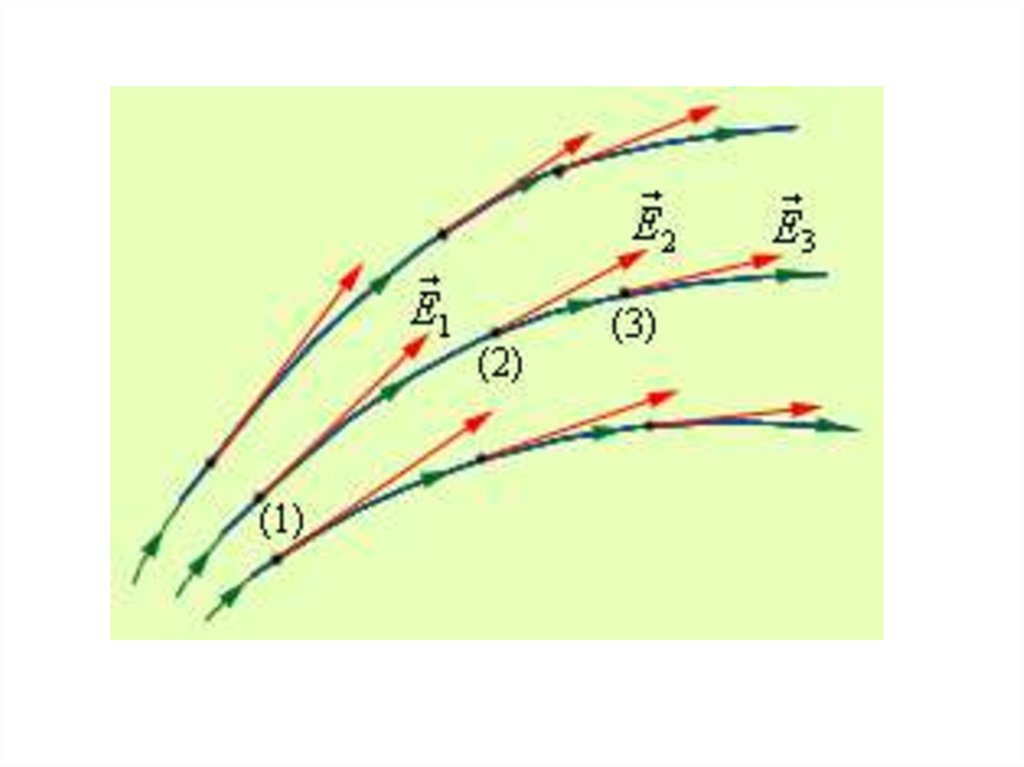
Для графического изображения поля используются силовыелинии. Касательные к силовым линиям совпадают с направлением
вектора напряженности в данной точке поля.
19.
20.
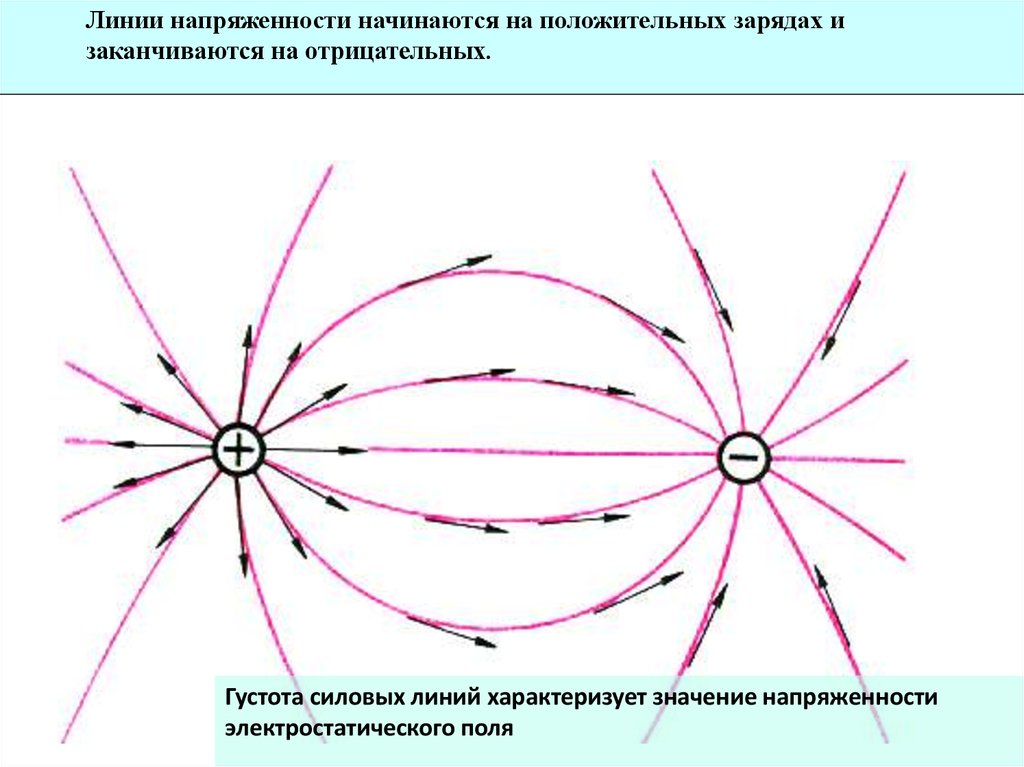
Линии напряженности начинаются на положительных зарядах изаканчиваются на отрицательных.
Густота силовых линий характеризует значение напряженности
электростатического поля
21.
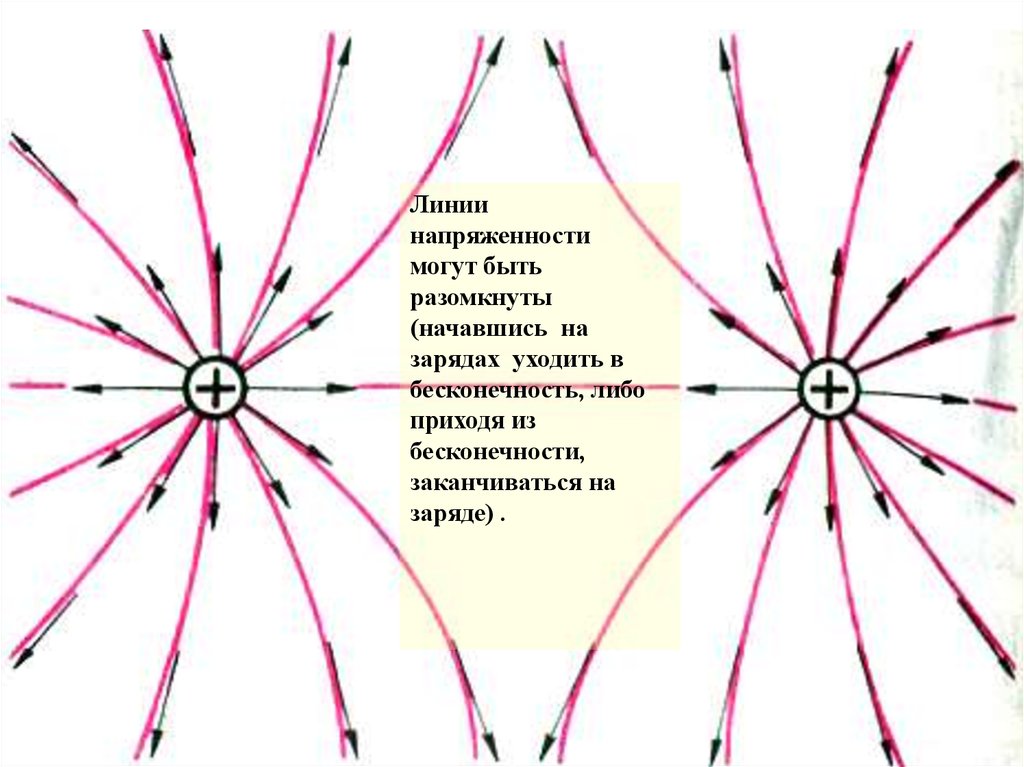
Линиинапряженности
могут быть
разомкнуты
(начавшись на
зарядах уходить в
бесконечность, либо
приходя из
бесконечности,
заканчиваться на
заряде) .
22.
23.
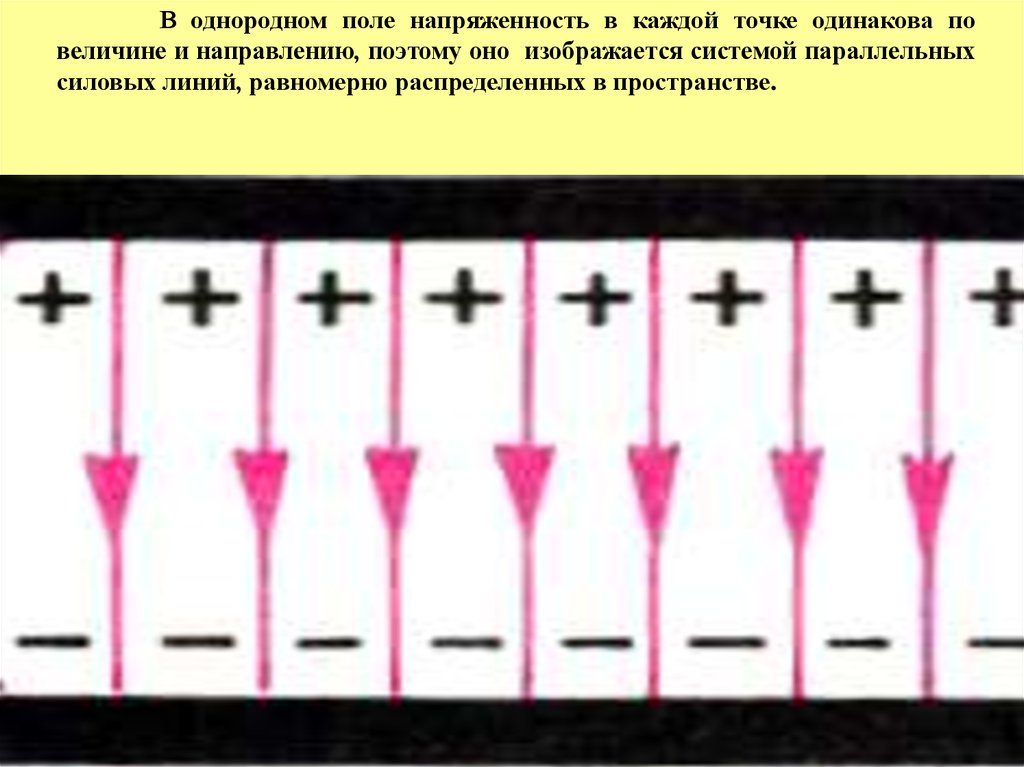
В однородном поле напряженность в каждой точке одинакова повеличине и направлению, поэтому оно изображается системой параллельных
силовых линий, равномерно распределенных в пространстве.
24.
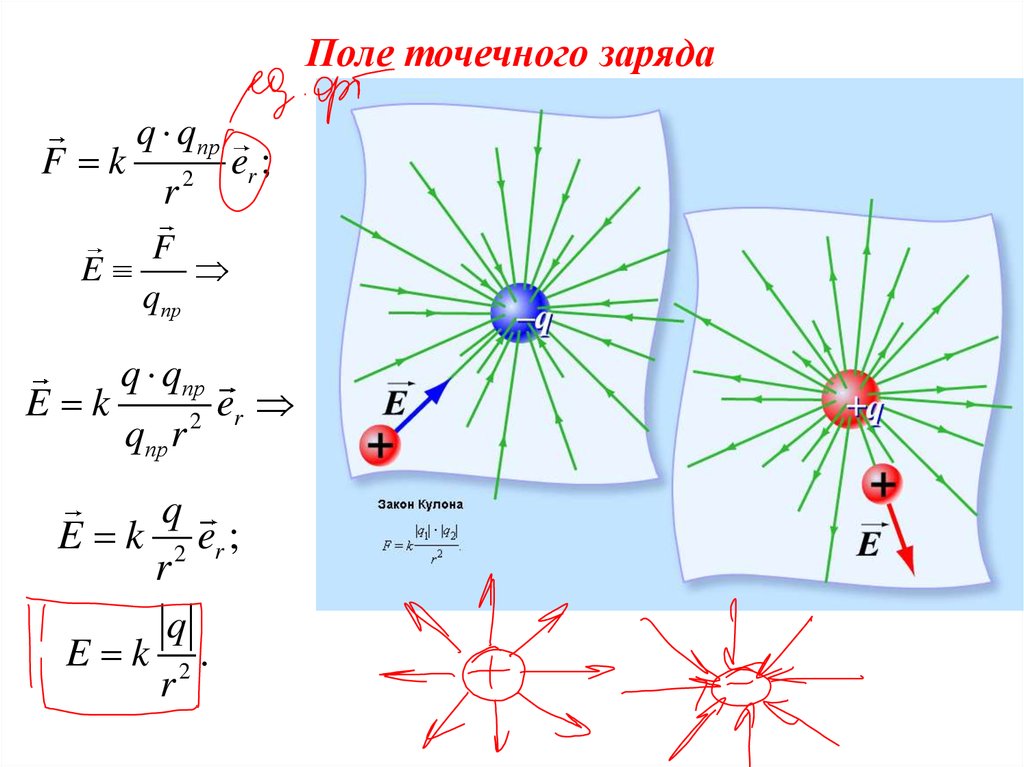
Поле точечного зарядаF k
q qпр
r
2
er ;
F
E
qпр
E k
q qпр
qпр r
2
er
q
E k 2 er ;
r
q
E k 2.
r
25.
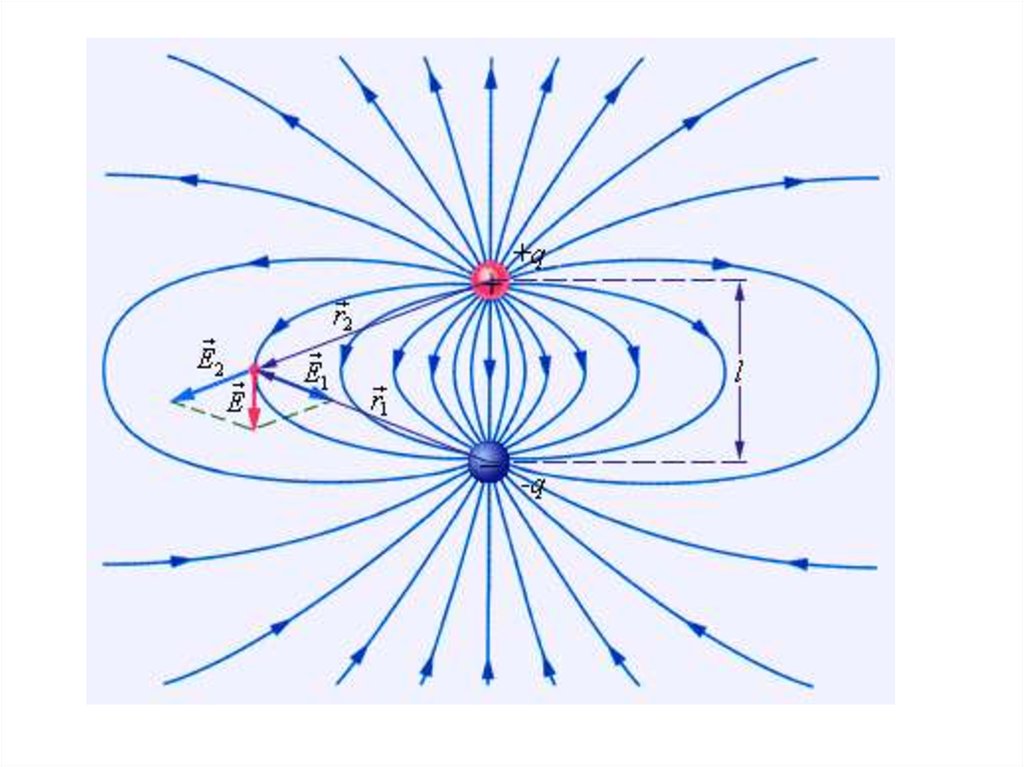
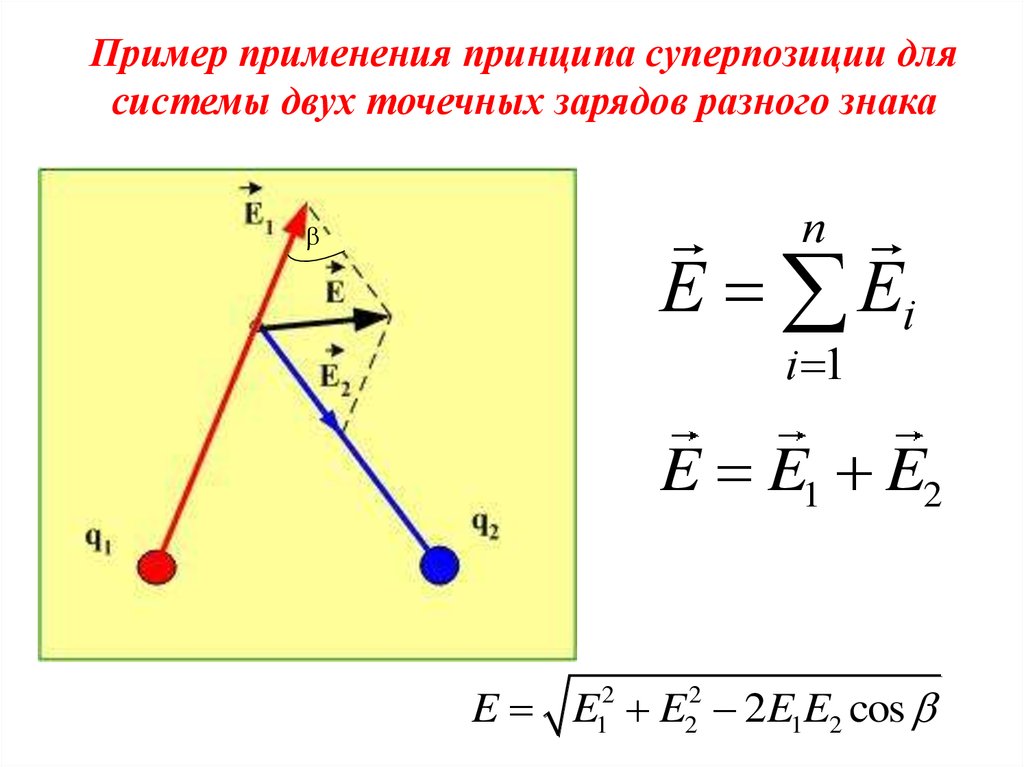
Пример применения принципа суперпозиции длясистемы двух точечных зарядов разного знака
n
E Ei
i 1
E E1 E2
E E12 E22 2E1E2 cos
26.
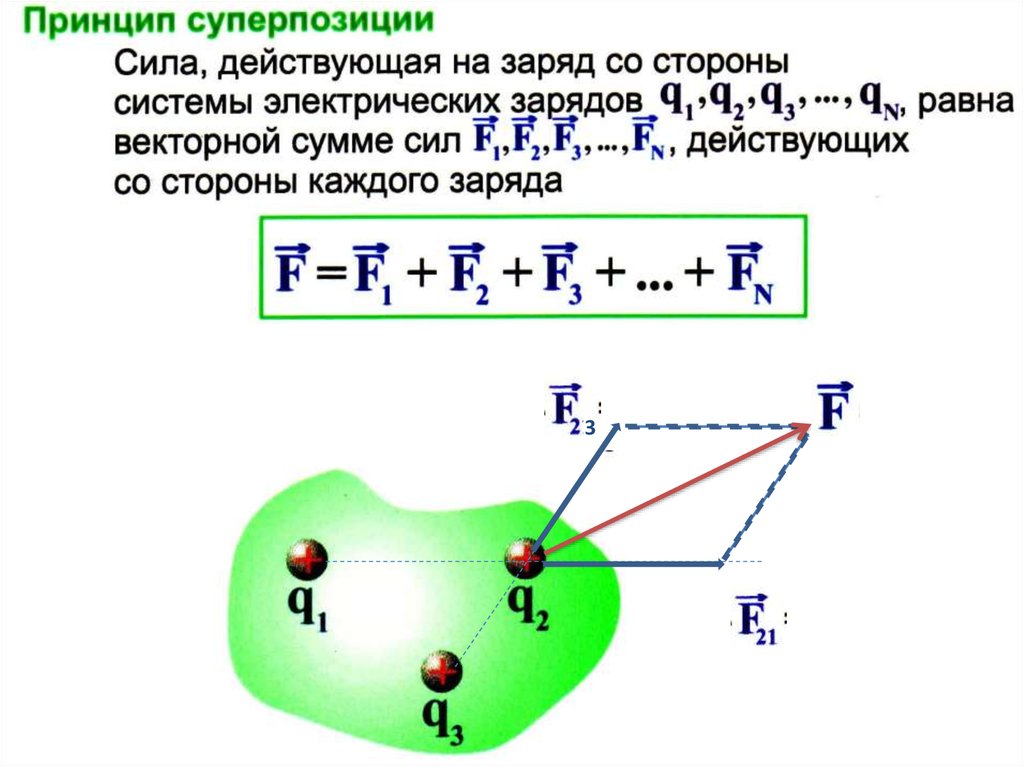
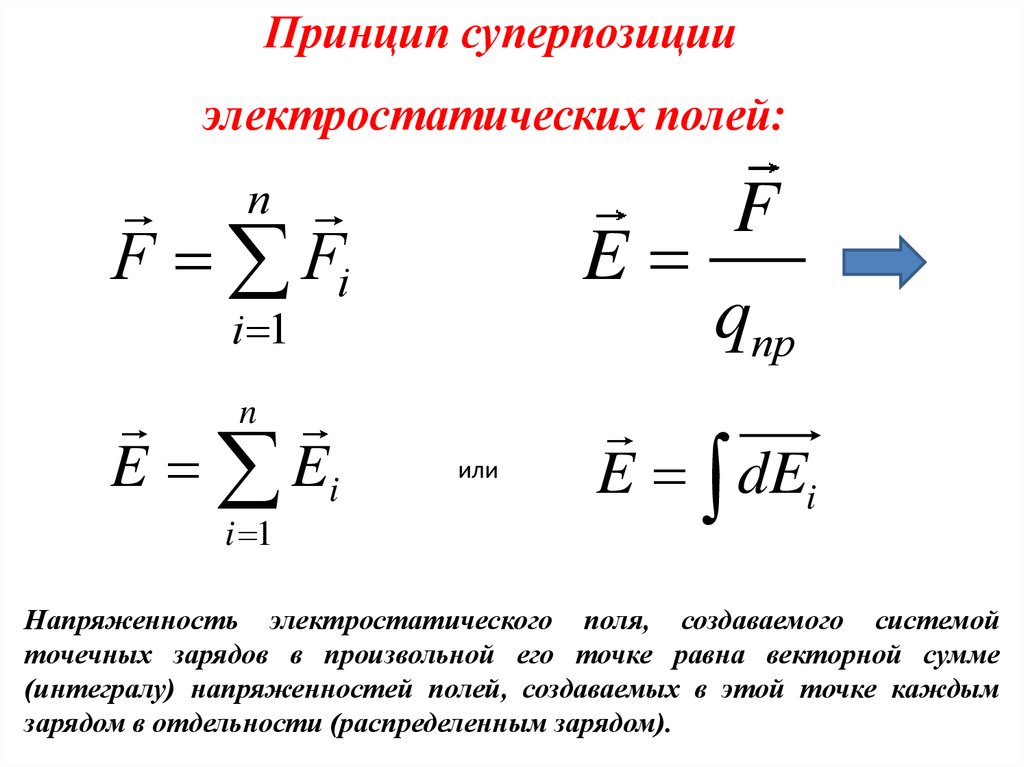
Принцип суперпозицииэлектростатических полей:
n
F Fi
F
E
qпр
i 1
n
E Ei
i 1
или
E dEi
Напряженность электростатического поля, создаваемого системой
точечных зарядов в произвольной его точке равна векторной сумме
(интегралу) напряженностей полей, создаваемых в этой точке каждым
зарядом в отдельности (распределенным зарядом).
27.
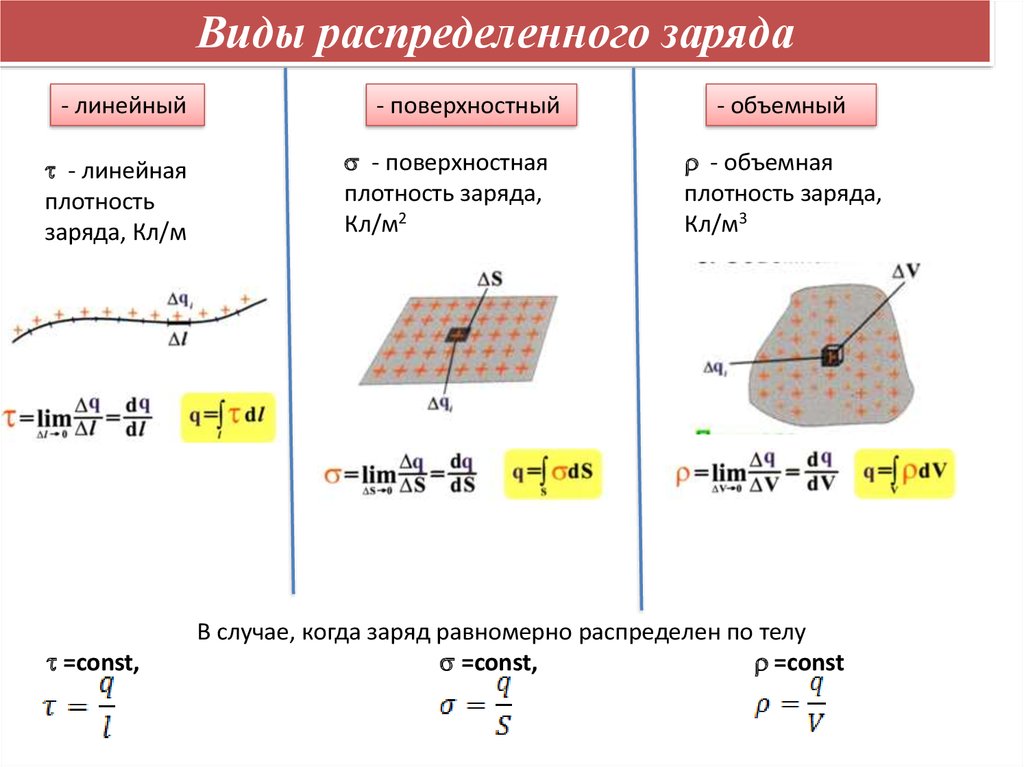
Виды распределенного заряда- линейный
- линейная
плотность
заряда, Кл/м
=const,
- поверхностный
- поверхностная
плотность заряда,
Кл/м2
- объемный
- объемная
плотность заряда,
Кл/м3
В случае, когда заряд равномерно распределен по телу
=const,
=const
28.
4. Примеры вычислениянапряжённости поля.
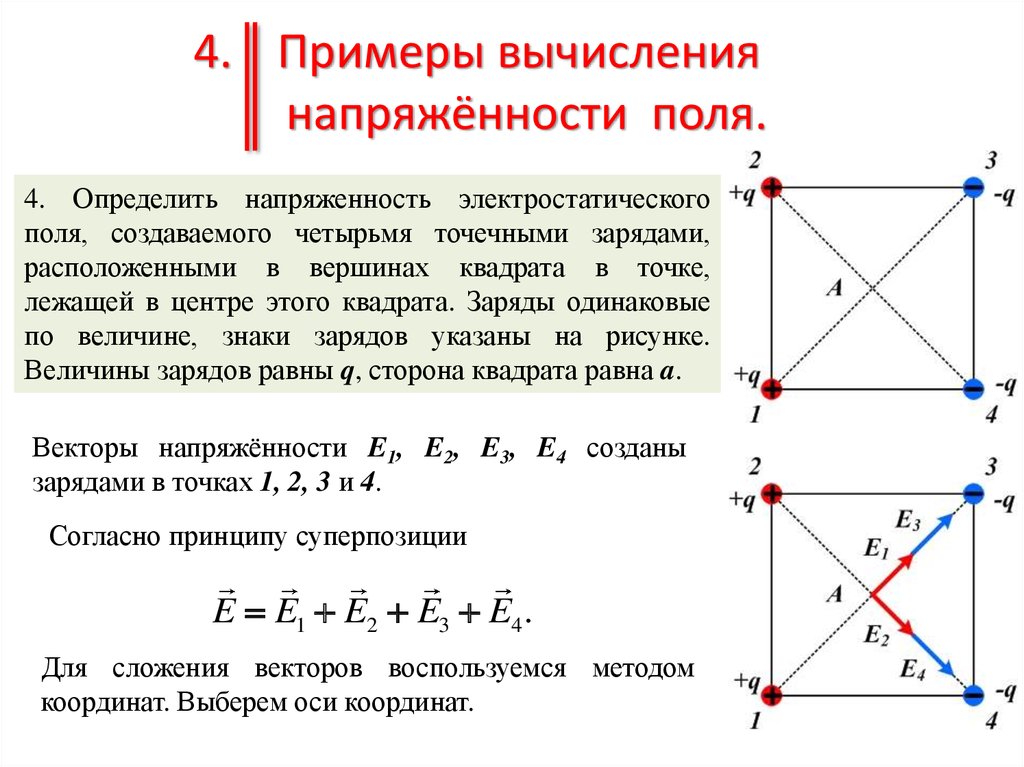
4. Определить напряженность электростатического
поля, создаваемого четырьмя точечными зарядами,
расположенными в вершинах квадрата в точке,
лежащей в центре этого квадрата. Заряды одинаковые
по величине, знаки зарядов указаны на рисунке.
Величины зарядов равны q, сторона квадрата равна a.
Векторы напряжённости E1, E2, E3, E4 созданы
зарядами в точках 1, 2, 3 и 4.
Согласно принципу суперпозиции
E E1 E2 E3 E4 .
Для сложения векторов воспользуемся методом
координат. Выберем оси координат.
29.
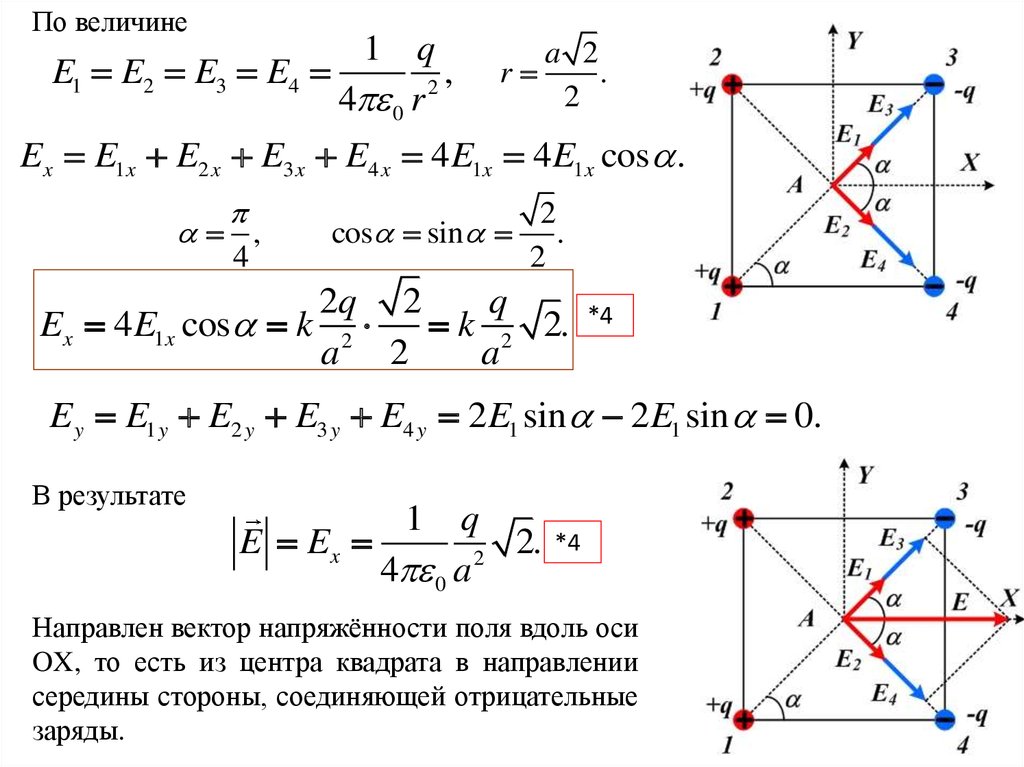
По величине1 q
E1 E2 E3 E4
,
2
4 0 r
r
a 2
.
2
Ex E1x E2 x E3 x E4 x 4 E1x 4 E1x cos .
,
4
cos sin
2
.
2
2q 2
q
Ex 4 E1x cos k 2
k 2 2.
a 2
a
*4
E y E1 y E2 y E3 y E4 y 2E1 sin 2E1 sin 0.
В результате
1
q
E Ex
2.
2
4 0 a
*4
Направлен вектор напряжённости поля вдоль оси
OX, то есть из центра квадрата в направлении
середины стороны, соединяющей отрицательные
заряды.
30.
5. Определить напряженность электростатического поля, создаваемого тонкимравномерно заряженным стержнем в точке, лежащей на его оси. Длина
стержня d, расстояние от конца стержня до точки наблюдения l. Заряд стержня
равен q.
Разделим стержень на множество малых отрезков, заряды которых можно
считать точечными. Тогда напряжённость поля, создаваемую каждым из этих
отрезков можно определять, как напряжённость поля точечного заряда.
dq
dE k 2 ,
r
q
dq dr dr ,
d
E dEi .
Согласно принципу суперпозиции
i
q
.
d
Все векторы dE сонаправлены, поэтому для модуля вектора напряжённости
E dEi
i
l d
dE .
l
31.
E dEii
dq
dE k 2 ,
r
l d
E
l
dq
k 2
r
l d
l
l d
dE .
l
q
dq dr dr ,
d
dr
q
.
d
1
1
d
k
k 2 k
.
r
l l d
l d l
q d
1
q
E k
.
d l l d 4 0 l l d
32.
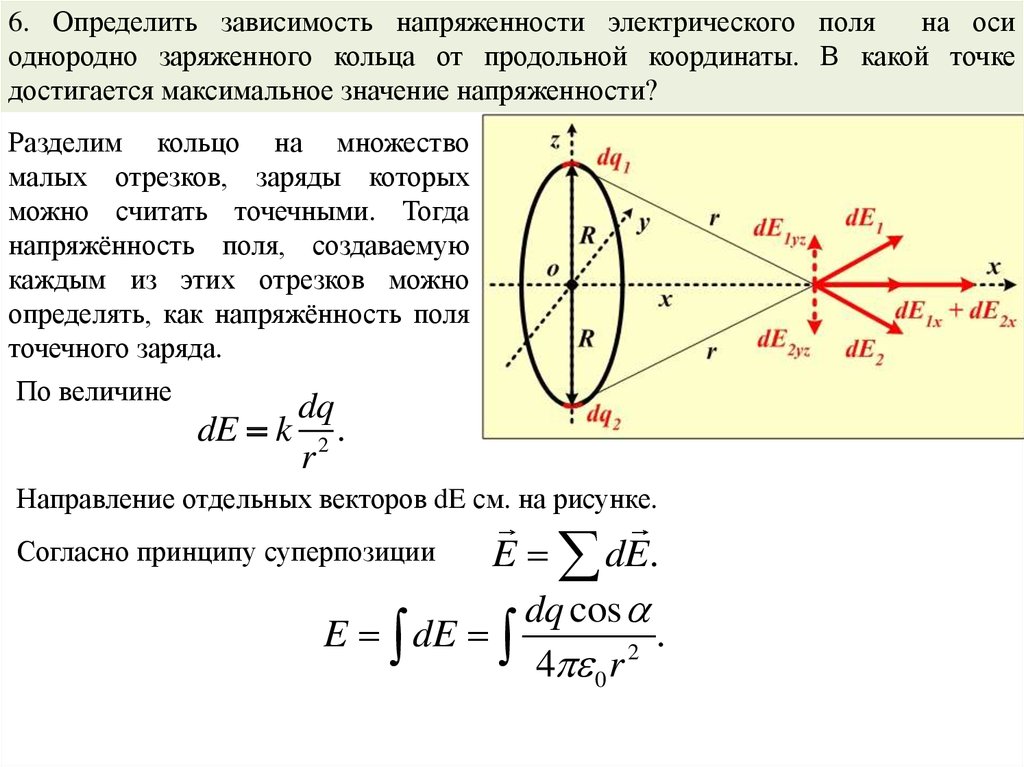
6. Определить зависимость напряженности электрического поляна оси
однородно заряженного кольца от продольной координаты. В какой точке
достигается максимальное значение напряженности?
Разделим кольцо на множество
малых отрезков, заряды которых
можно считать точечными. Тогда
напряжённость поля, создаваемую
каждым из этих отрезков можно
определять, как напряжённость поля
точечного заряда.
По величине
dq
dE k 2 .
r
Направление отдельных векторов dE см. на рисунке.
E dE.
dq cos
E dE
.
2
4 0 r
Согласно принципу суперпозиции
33.
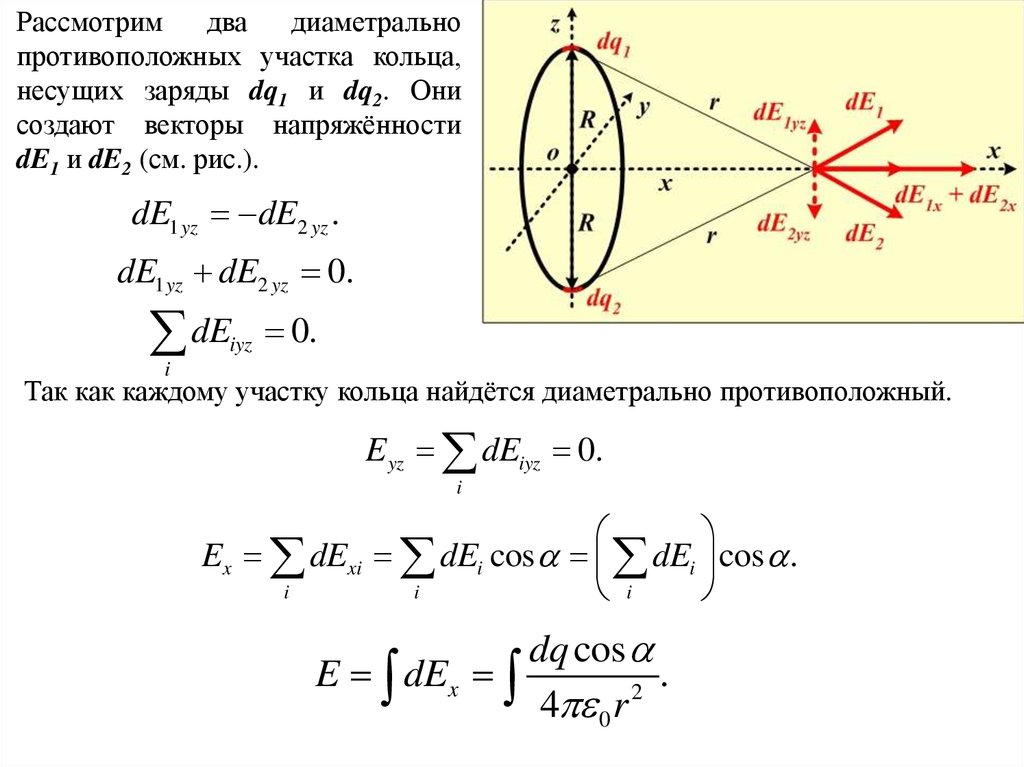
Рассмотримдва
диаметрально
противоположных участка кольца,
несущих заряды dq1 и dq2. Они
создают векторы напряжённости
dE1 и dE2 (см. рис.).
dE1 yz dE2 yz .
dE1 yz dE2 yz 0.
dE
iyz
0.
i
Так как каждому участку кольца найдётся диаметрально противоположный.
E yz dEiyz 0.
i
Ex dExi dEi cos dEi cos .
i
i
i
dq cos
E dEx
.
2
4 0 r
34.
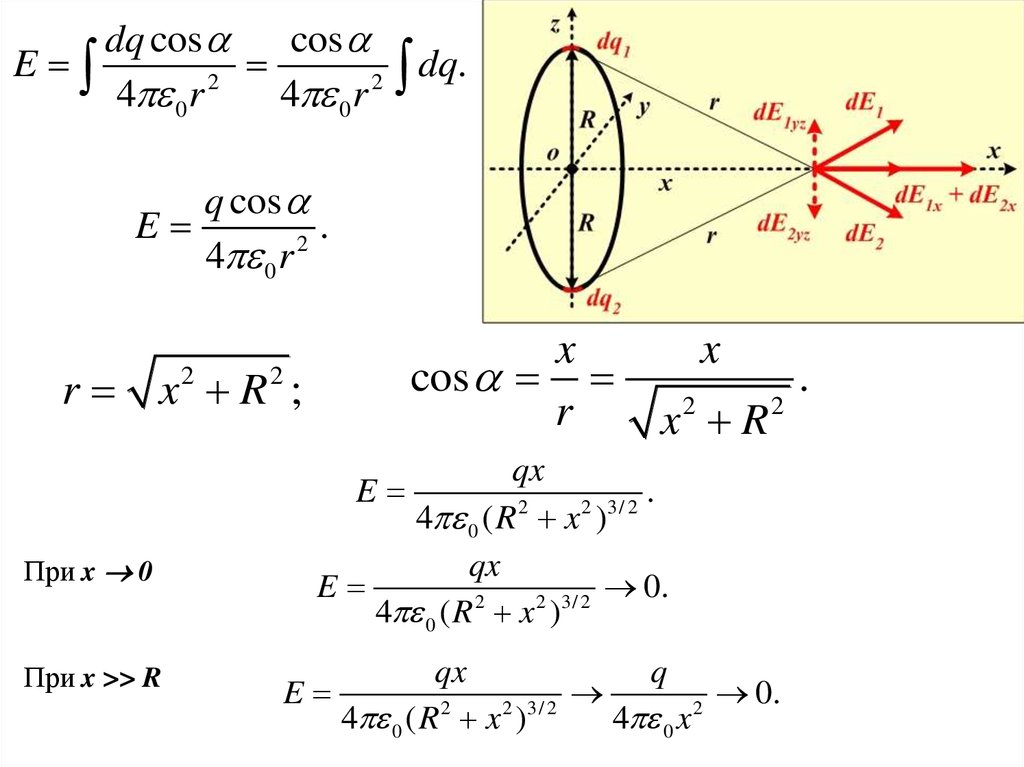
dq coscos
E
dq.
2
2
4 0 r
4 0 r
q cos
E
.
2
4 0 r
r x R ;
2
При x 0
При x >> R
2
x
cos
r
x
x R
2
2
qx
E
.
2
2 3/ 2
4 0 ( R x )
qx
E
0.
2
2 3/ 2
4 0 ( R x )
qx
q
E
0.
2
2 3/ 2
2
4 0 ( R x )
4 0 x
.
35.
У такой функции должен быть хотя бы один максимум.Условие экстремума (максимума):
dE ( x)
0.
dx
2
2 3/ 2
2
2 1/ 2
dE ( x) 4 0 q[( R x ) 3 / 2 ( R x ) 2 x x]
0.
2
2
2 3
dx
(4 0 ) ( R x )
3 2
( R x ) ( R x 2 )1/ 2 2 x 2 0;
2
( R2 x2 )1/ 2 ( R2 x2 ) 3x2 0;
2
2 3/ 2
( R 2 x 2 ) 3x 2 0;
x
R
2
R 2 2 x 2 0.
36.
7. Определить зависимость напряженности электрического поля на прямой,перпендикулярной однородно заряженной бесконечной тонкой нити от
продольной координаты.
Разделим нить на множество малых отрезков,
заряды которых можно считать точечными. Тогда
напряжённость поля, создаваемую каждым из
этих
отрезков
можно
определять,
как
напряжённость поля точечного заряда.
По величине
dq
dE k 2 .
r
Направление отдельных векторов dE см. на
рисунке.
Согласно принципу суперпозиции
E dE.
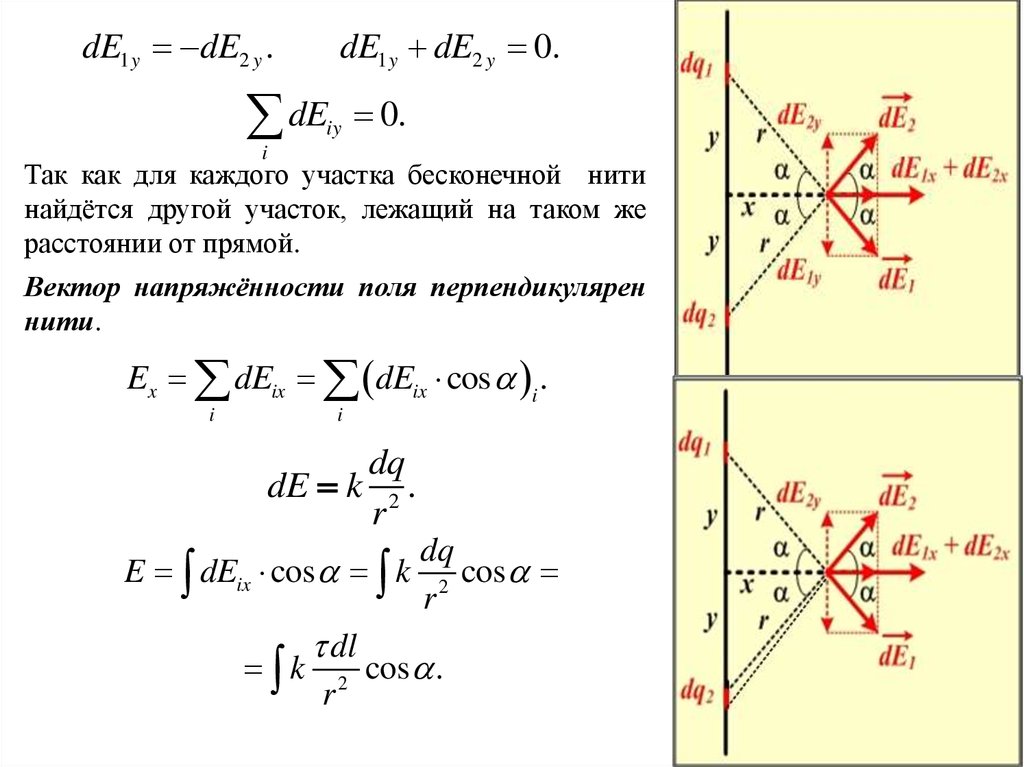
Рассмотрим два участка кольца, расположенных на одинаковых расстояниях от
рассматриваемой прямой и несущих заряды dq1 и dq2. Они создают векторы
напряжённости dE1 и dE2 (см. рис.).
dE1 y dE2 y .
37.
dE1 y dE2 y .dE1 y dE2 y 0.
dE
iy
0.
i
Так как для каждого участка бесконечной нити
найдётся другой участок, лежащий на таком же
расстоянии от прямой.
Вектор напряжённости поля перпендикулярен
нити.
Ex dEix dEix cos i .
i
i
dq
dE k 2 .
r
dq
E dEix cos k 2 cos
r
dl
k 2 cos .
r
38.
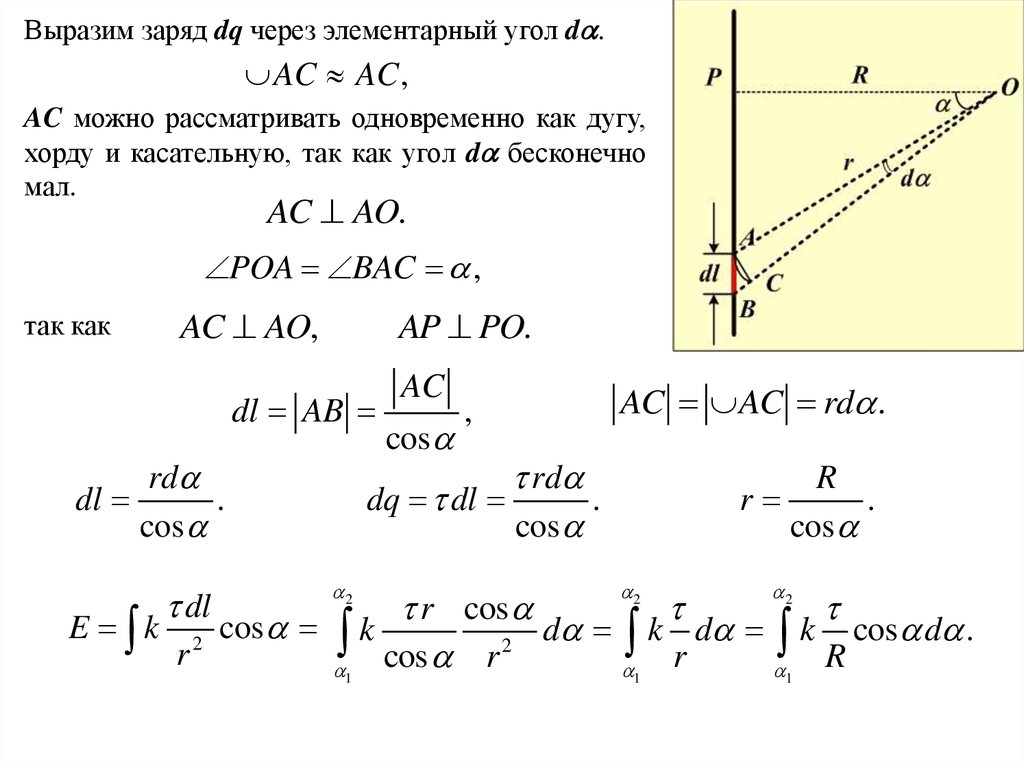
Выразим заряд dq через элементарный угол d .AC AC ,
AC можно рассматривать одновременно как дугу,
хорду и касательную, так как угол d бесконечно
мал.
AC AO.
POA BAC ,
так как
AC AO,
AP PO.
dl AB
cos
,
AC AC rd .
rd
dq dl
.
cos
rd
dl
.
cos
dl
AC
R
r
.
cos
2
2
2
1
1
1
r cos
E k 2 cos k
d k d k cos d .
2
r
cos r
r
R
39.
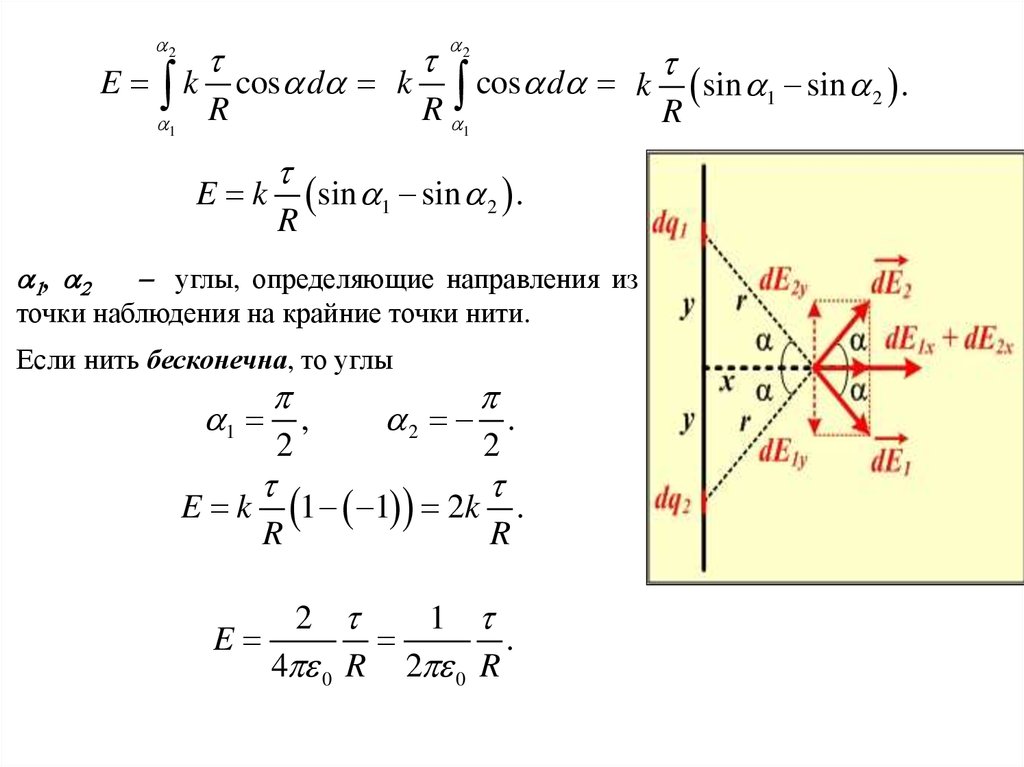
2E k
1
R
cos d k
E k
1, 2
R
2
cos d k
R 1
sin 1 sin 2 .
углы, определяющие направления из
точки наблюдения на крайние точки нити.
Если нить бесконечна, то углы
1
E k
2
,
2 .
2
1 1 2k .
R
R
2
1
E
.
4 0 R 2 0 R
R
sin 1 sin 2 .








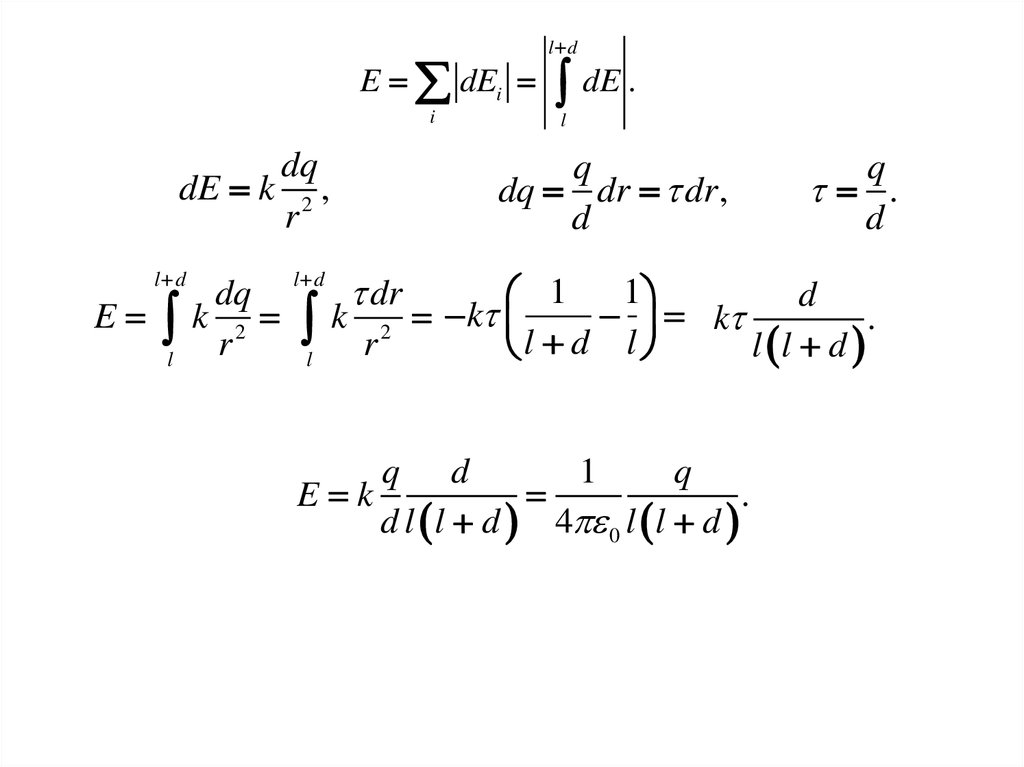


 Физика
Физика








