ВиС 9 класс 15 урок

ОТВЕТЬТЕ
НА
ВОПРОСЫ
01
Что
такое
испытание
Бернулли?
Приведите примеры испытаний.
02
Чему равна сумма вероятностей успеха
и неудачи?
03
Сколько элементарных событий в опыте
“испытание до первого успеха”?
04
Запишите
формулой
вероятность
события “произошло восемь неудач, а
при девятой попытке случился успех”.
05
кАКИМИ ДОЛЖНЫ БЫТЬ ИСПЫТАНИЯ, ЧТОБЫ
ПОЛУЧИЛАСЬ СЕРИЯ ИСПЫТАНИЙ БЕРНУЛЛИ?
06
кАКИМИ ДОЛЖНЫ БЫТЬ ИСПЫТАНИЯ, ЧТОБЫ
ПОЛУЧИЛАСЬ СЕРИЯ ИСПЫТАНИЙ БЕРНУЛЛИ?

3.

работаем
устно

4.

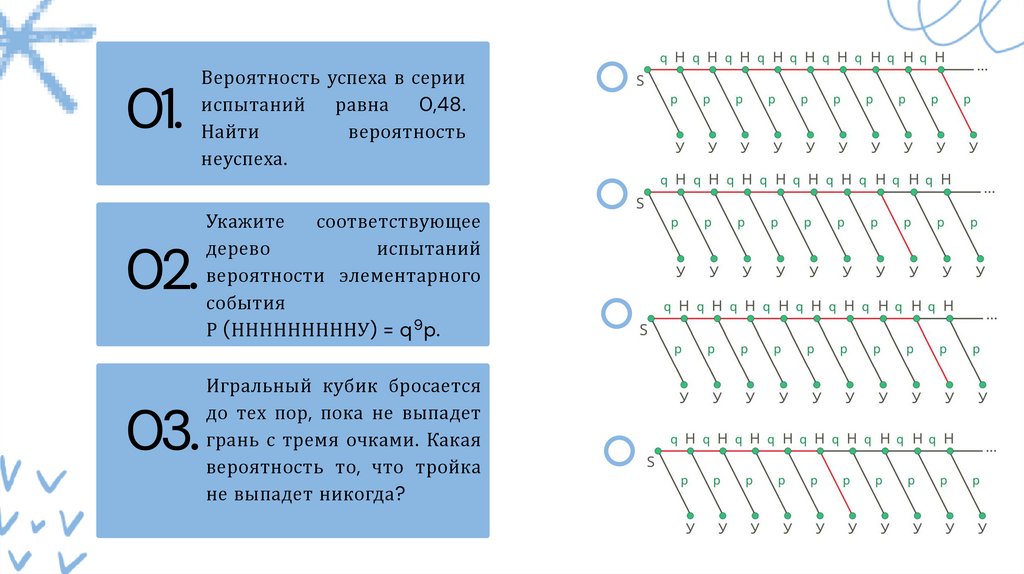
01.
Вероятность успеха в серии
испытаний равна 0,48.
Найти
вероятность
неуспеха.
02.
Укажите
соответствующее
дерево
испытаний
вероятности элементарного
события
Р (НННННННННУ) = q 9 p.
03.
Игральный кубик бросается
до тех пор, пока не выпадет
грань с тремя очками. Какая
вероятность то, что тройка
не выпадет никогда?

5.

работаем
в
тетради

6.

01.
Найдите
вероятность
элементарного события, в
котором вероятность успеха
испытания равна
р = 0,7, а перед успехом
случилось ровно 3 неуспеха.
решение:
Событию А “перед успехом случилось
ровно 3 неуспеха” благоприятствуют
элементарные события НННУ
Р (А) = q 3 p
q = 1 - p = 1 - 0,7 = 0,3.
P (A) = 0,3 3 ⋅ 0,7 = 0,0189.

7.

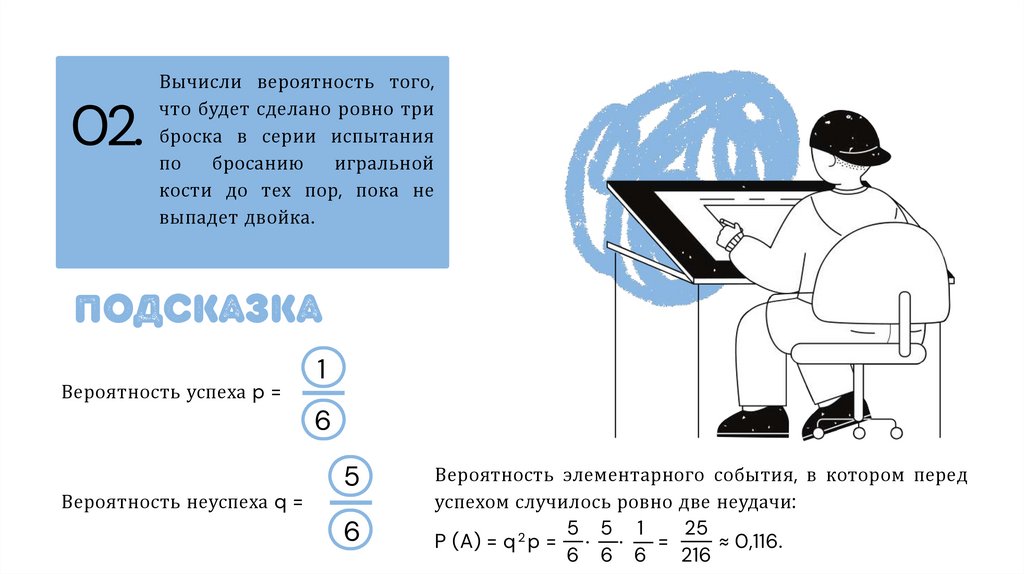
02.
Вычисли вероятность того,
что будет сделано ровно три
броска в серии испытания
по
бросанию
игральной
кости до тех пор, пока не
выпадет двойка.
подсказка:
Вероятность успеха p =
Вероятность неуспеха q =
1
6
5
6
Вероятность элементарного события, в котором перед
успехом случилось ровно две неудачи:
5 5 1
25
2
P (A) = q p = ⋅ ⋅
=
≈ 0,116.
6 6 6
216

8.

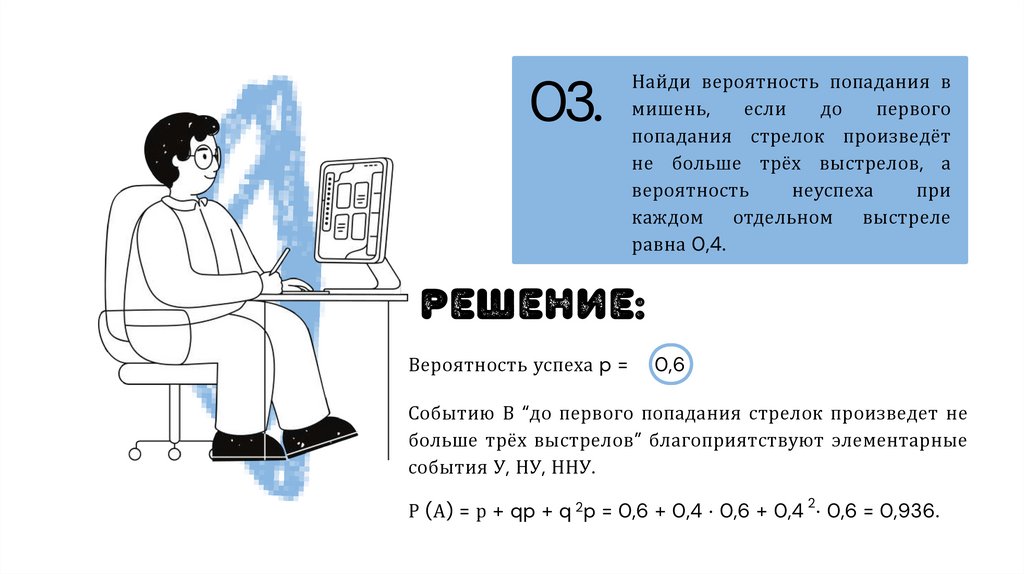
03.
Найди вероятность попадания в
мишень,
если
до
первого
попадания стрелок произведёт
не больше трёх выстрелов, а
вероятность
неуспеха
при
каждом отдельном выстреле
равна 0,4.
решение:
Вероятность успеха p =
0,6
Событию В “до первого попадания стрелок произведет не
больше трёх выстрелов” благоприятствуют элементарные
события У, НУ, ННУ.
2
2
Р (А) = р + qp + q p = 0,6 + 0,4 ⋅ 0,6 + 0,4 ⋅ 0,6 = 0,936.

9.

самостоятельная
работа

10.

i
ii
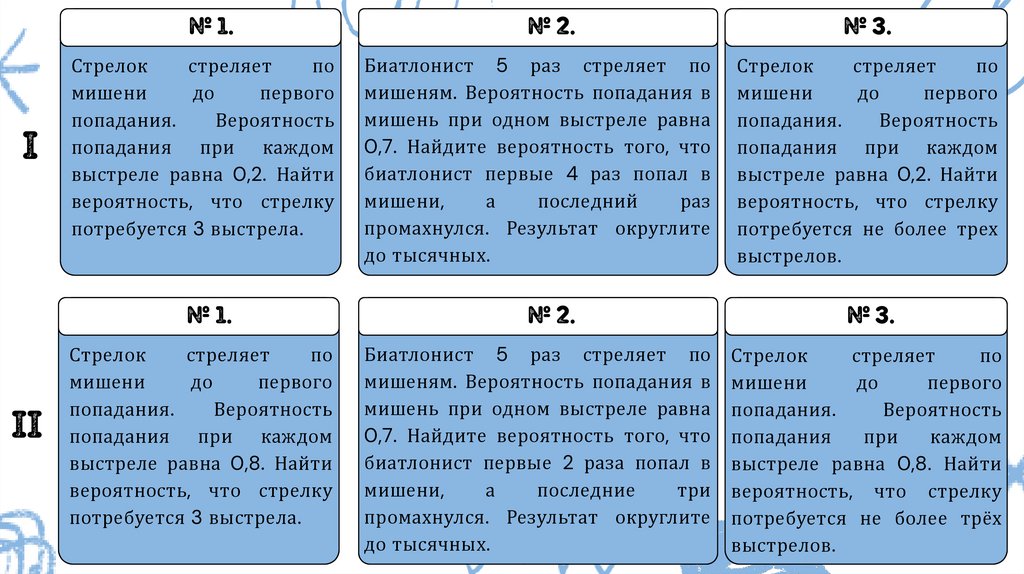
№ 1.
№ 2.
№ 3.
Стрелок
стреляет
по
мишени
до
первого
попадания.
Вероятность
попадания при каждом
выстреле равна 0,2. Найти
вероятность, что стрелку
потребуется 3 выстрела.
Биатлонист 5 раз стреляет по
мишеням. Вероятность попадания в
мишень при одном выстреле равна
0,7. Найдите вероятность того, что
биатлонист первые 4 раз попал в
мишени,
а
последний
раз
промахнулся. Результат округлите
до тысячных.
Стрелок
стреляет
по
мишени
до
первого
попадания.
Вероятность
попадания при каждом
выстреле равна 0,2. Найти
вероятность, что стрелку
потребуется не более трех
выстрелов.
№ 1.
№ 2.
№ 3.
Стрелок
стреляет
по
мишени
до
первого
попадания.
Вероятность
попадания при каждом
выстреле равна 0,8. Найти
вероятность, что стрелку
потребуется 3 выстрела.
Биатлонист 5 раз стреляет по
мишеням. Вероятность попадания в
мишень при одном выстреле равна
0,7. Найдите вероятность того, что
биатлонист первые 2 раза попал в
мишени,
а
последние
три
промахнулся. Результат округлите
до тысячных.
Стрелок
стреляет
по
мишени
до
первого
попадания.
Вероятность
попадания
при
каждом
выстреле равна 0,8. Найти
вероятность, что стрелку
потребуется не более трёх
выстрелов.

11.

домашнее
задание
§ 65, стр 74 № 223, 224

English Русский Правила