10_алгебра_26.01.26_Синус_ косинус и тангенс числового аргумента

1.

Функции синус, косинус,
тангенс, котангенс

2.

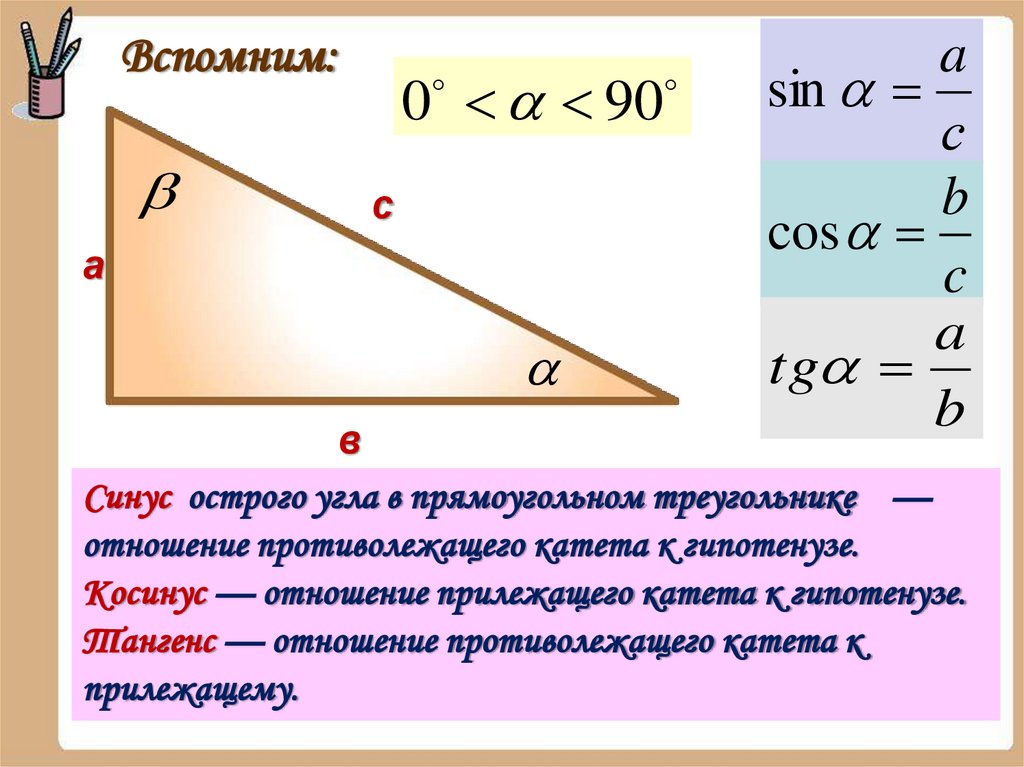
Вспомним:
0 90
с
а
a
sin
с
b
cos
c
a
tg
b
в
Синус острого угла в прямоугольном треугольнике —
отношение противолежащего катета к гипотенузе.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к
прилежащему.

3.

В XVIII веке Леонард Эйлер
дал современные, более
общие определения,
расширив область
определения этих функций
на всю числовую ось.
угол _ поворота
R

4.

у
1
0
х
1

5.

у
1
0
х
1

6.

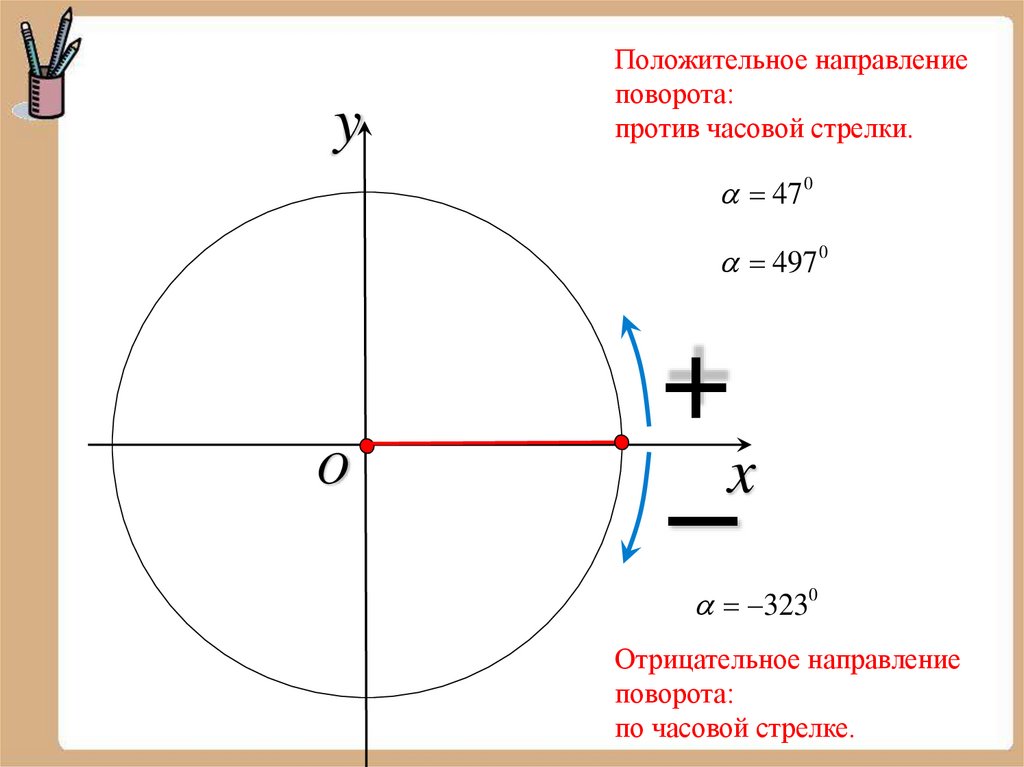
y
Положительное направление
поворота:
против часовой стрелки.
47 0
497 0
O
+
x
–
3230
Отрицательное направление
поворота:
по часовой стрелке.

7.

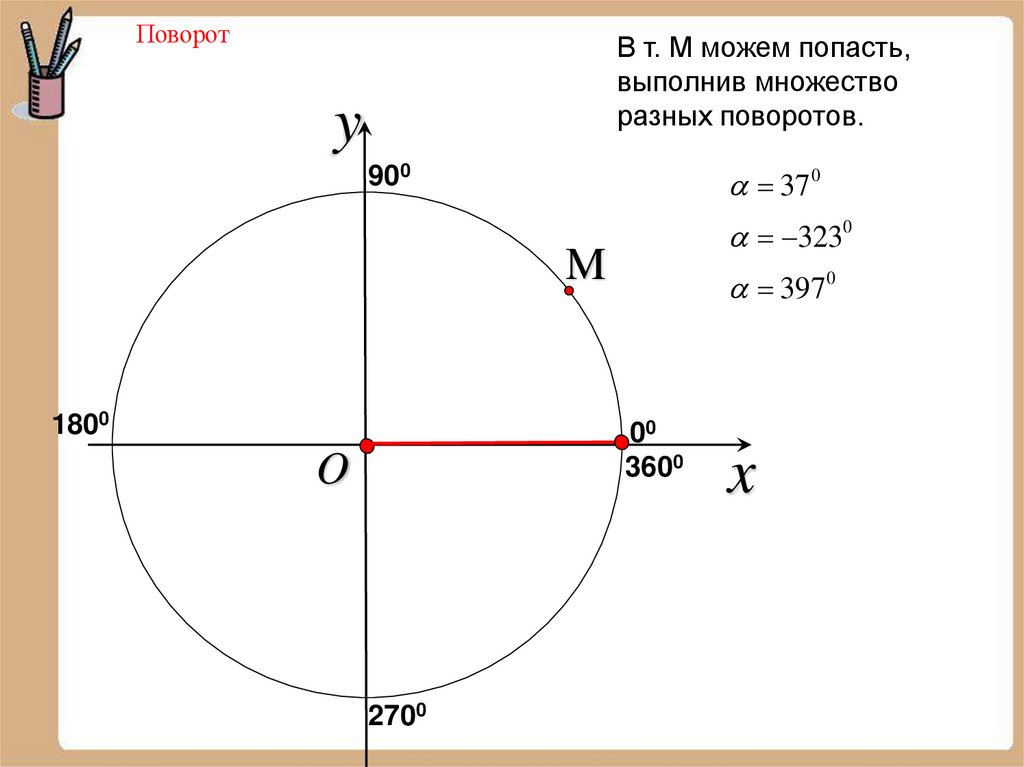
Поворот
В т. М можем попасть,
выполнив множество
разных поворотов.
y
37 0
900
3230
M
1800
3970
00
3600
O
2700
x

8.

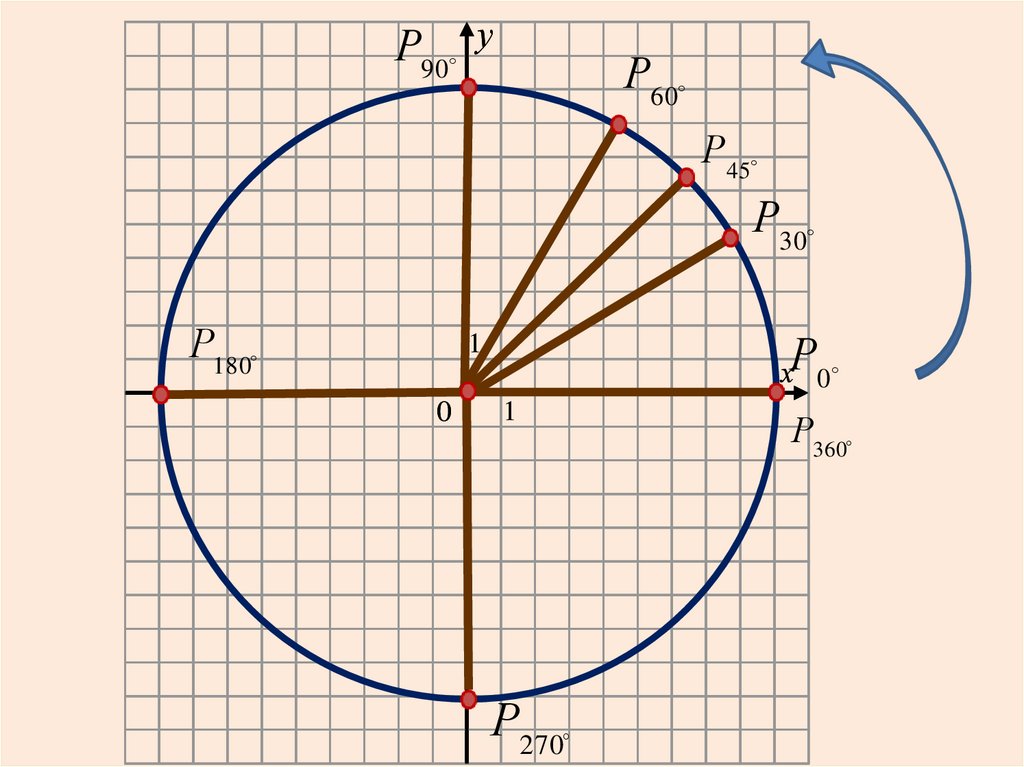
Р90 у
Р60
Р45
Р30
Р180
Р
1
0
х 0
1
Р270
Р360

9.

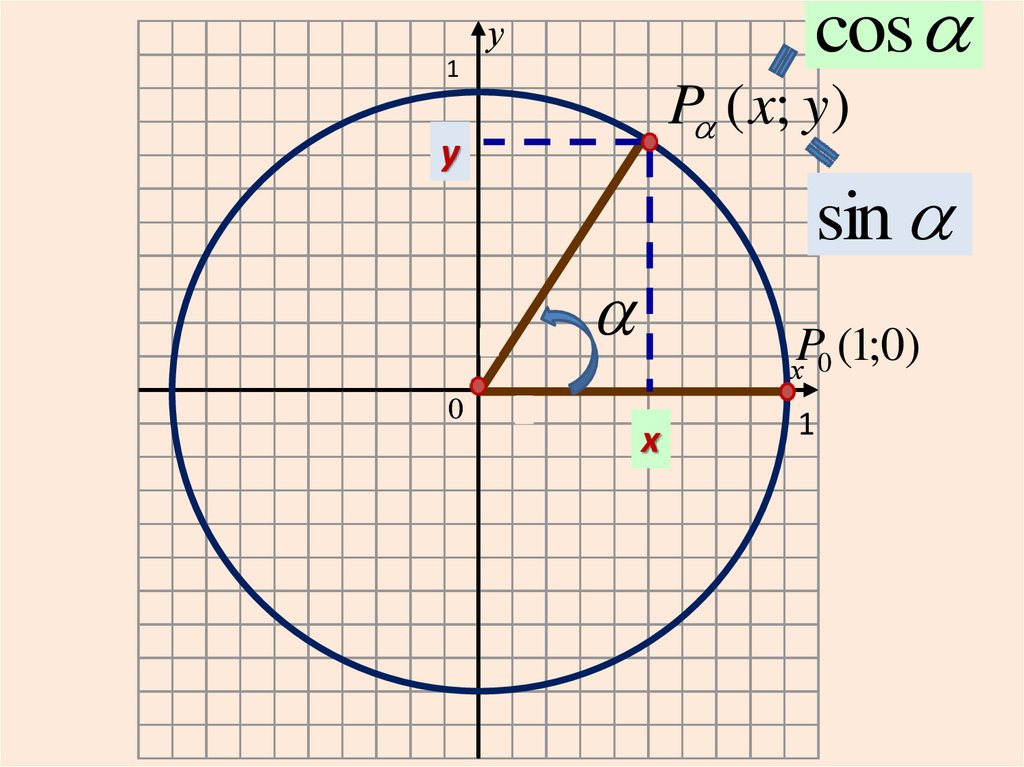
cos
у
1
P ( x; y)
у
sin
1
0
P (1;0)
х 0
1
х
1

10.

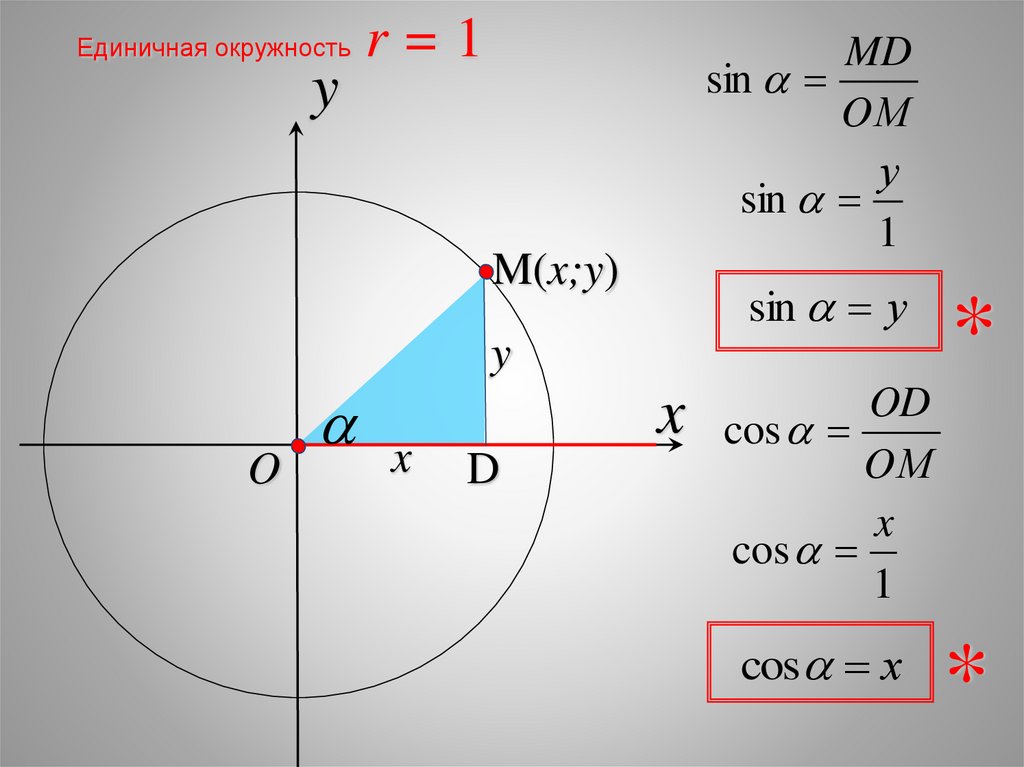
Единичная окружность
y
r=1
M(x;y)
MD
sin
OМ
у
sin
1
sin у
y
O
x
D
*
x cos OD
OМ
x
cos
1
cos х
*

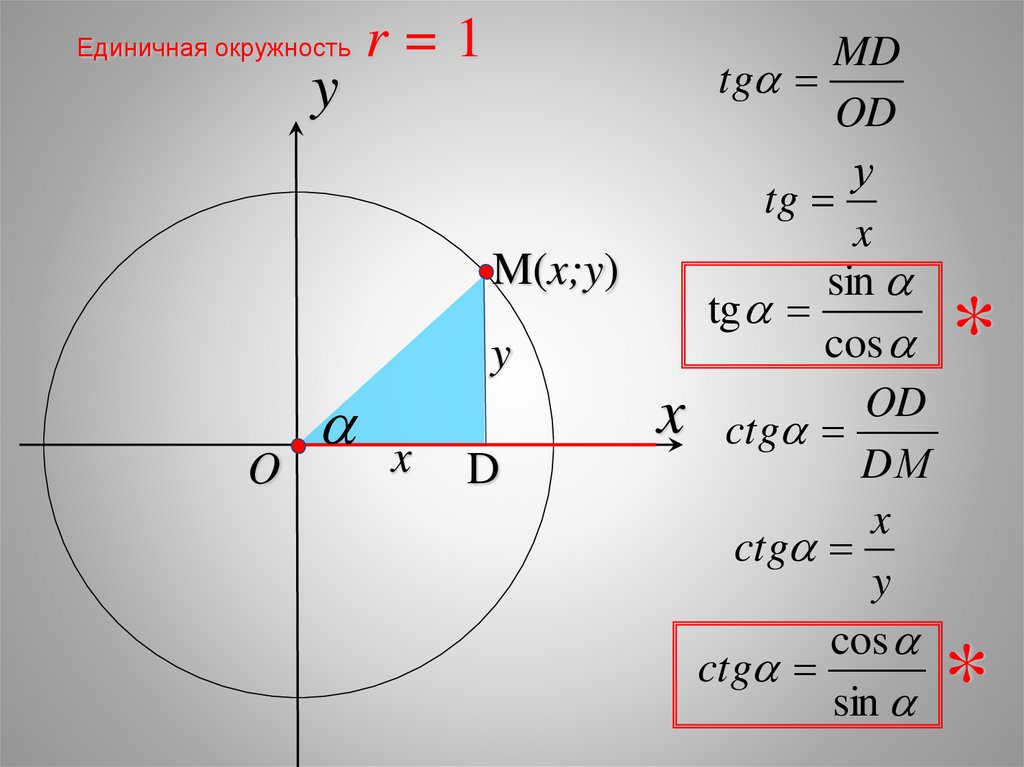
11.

Единичная окружность
y
O
r=1
x
MD
tg
OD
у
tg
x
M(x;y)
sin
tg
cos
y
x ctg OD
DМ
D
x
ctg
y
cos
ctg
sin
*
*

12.

sin y
cos x
Косинус — абсцисса точки P
y
tg
Тангенс – отношение
ординаты к абсциссе
точки P x
x
Котангенс – отношение
ctgточки
абсциссы
к ординате
P y
Синус угла определяется как ордината
точки P

13.

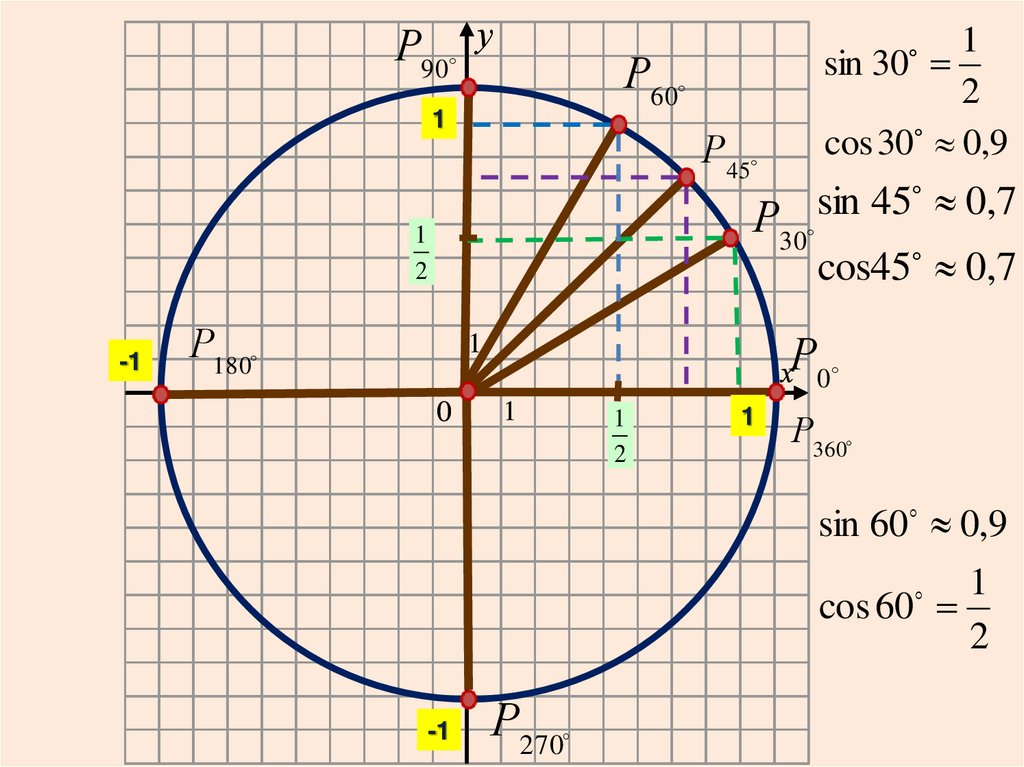
Р90 у
Р60
1
Р45
sin
45
0,7
Р30
cos45 0,7
1
2
-1
1
sin 30
2
cos 30 0,9
Р180
Р
1
0
х 0
1
1
2
1
Р360
sin 60 0,9
1
cos 60
2
-1
Р270

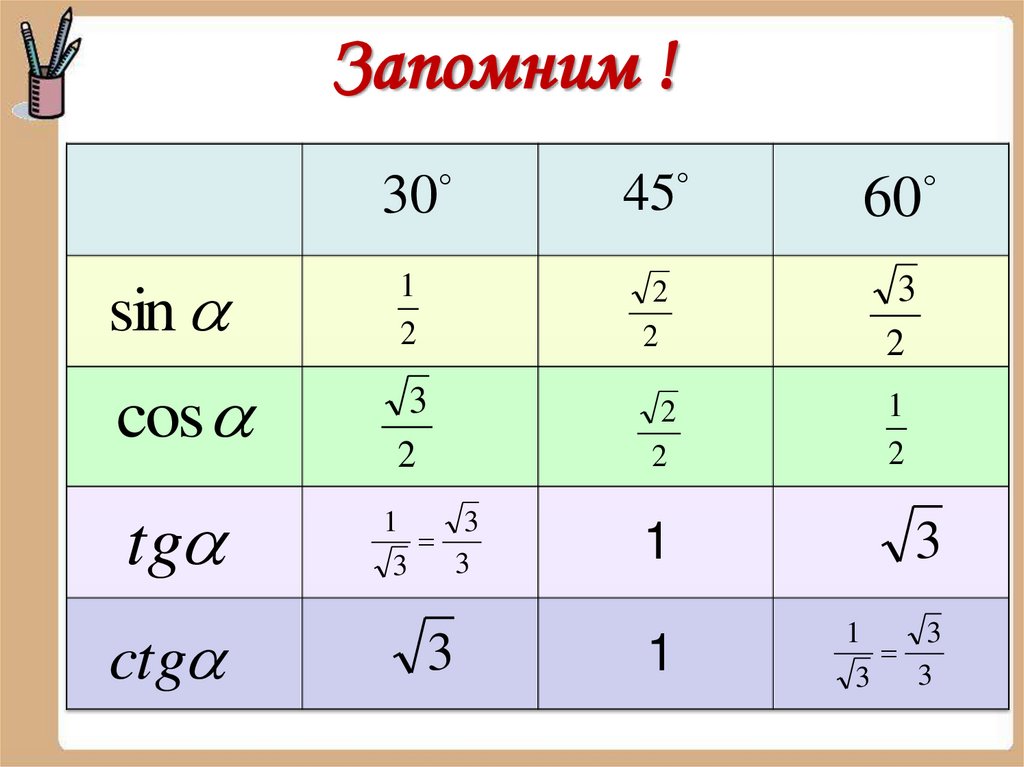
14.

Запомним !
cos
tg
ctg
45
60
1
2
2
2
3
2
3
2
2
2
1
2
1
3
3
3
1
3
1
1
3
3
3
30
sin
3

15.

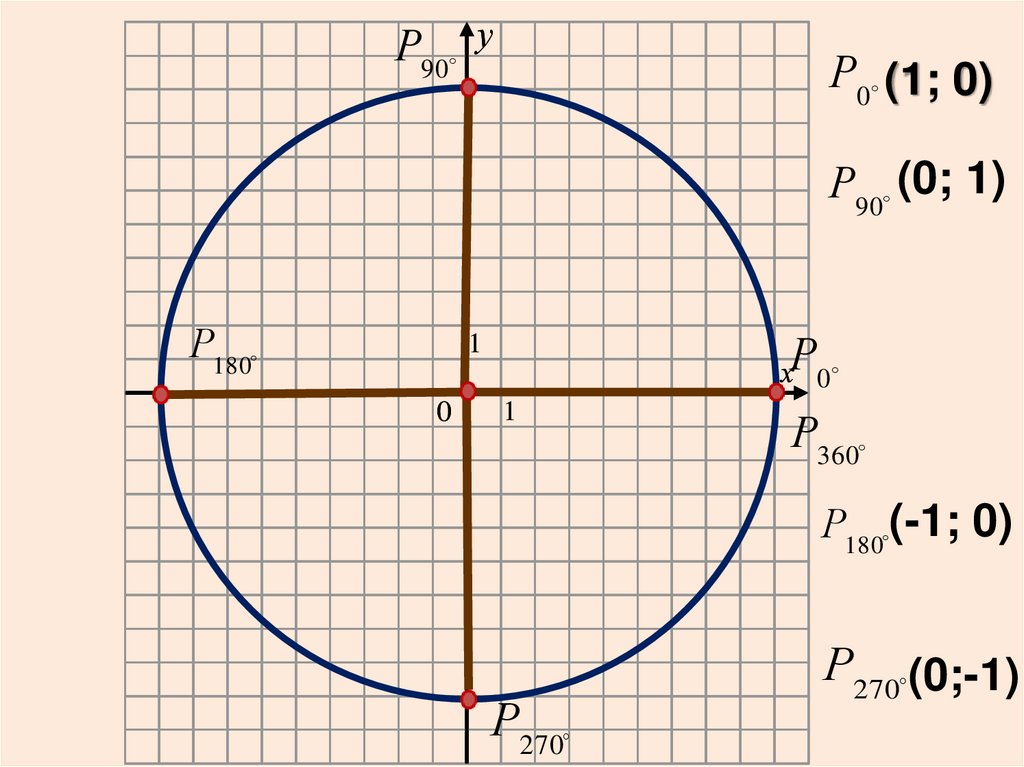
Р90 у
Р0 (1; 0)
Р90 (0; 1)
Р180
Р
1
0
х 0
1
Р360
Р180 (-1; 0)
Р270
Р270 (0;-1)

16.

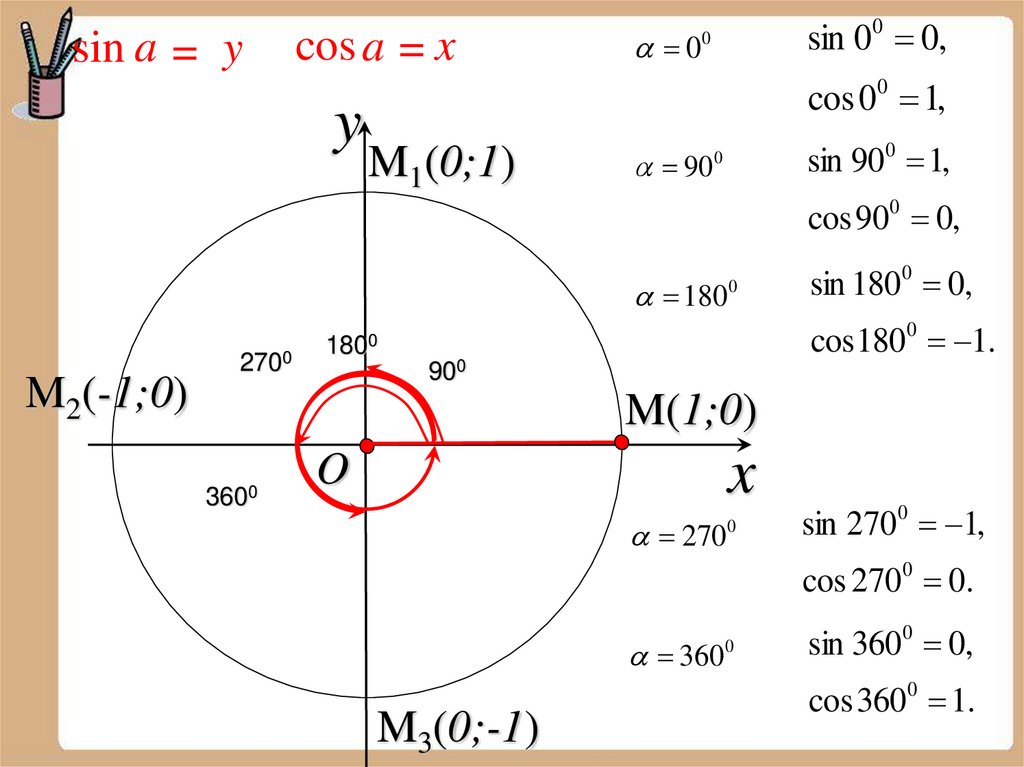
sin a = y
cos a = x
y
0
sin 00 0,
0
cos 00 1,
M1(0;1)
90
sin 900 1,
0
cos 900 0,
180
M2(-1;0)
2700
0
sin 1800 0,
cos1800 1.
1800
900
M(1;0)
3600
x
O
270
0
sin 2700 1,
cos 2700 0.
360
M3(0;-1)
0
sin 3600 0,
cos 3600 1.

17.

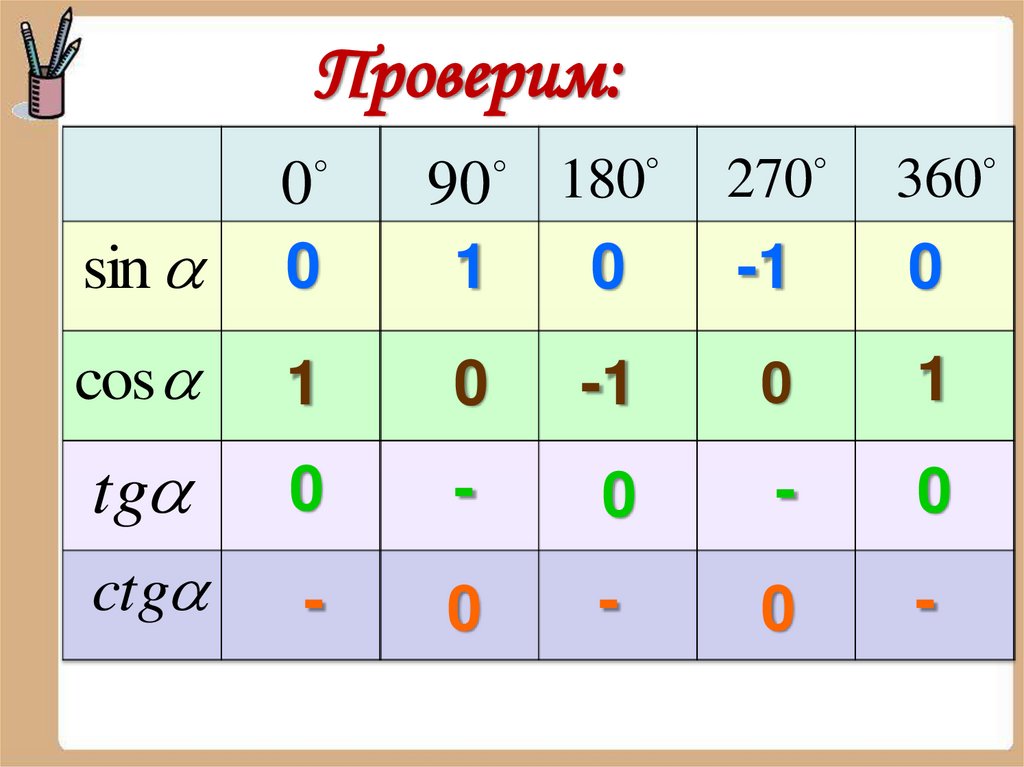
Проверим:
180
270
0
-1
0
0
-1
0
1
0
-
0
-
0
-
0
-
0
-
sin
0
0
90
1
cos
1
tg
ctg
360

18.

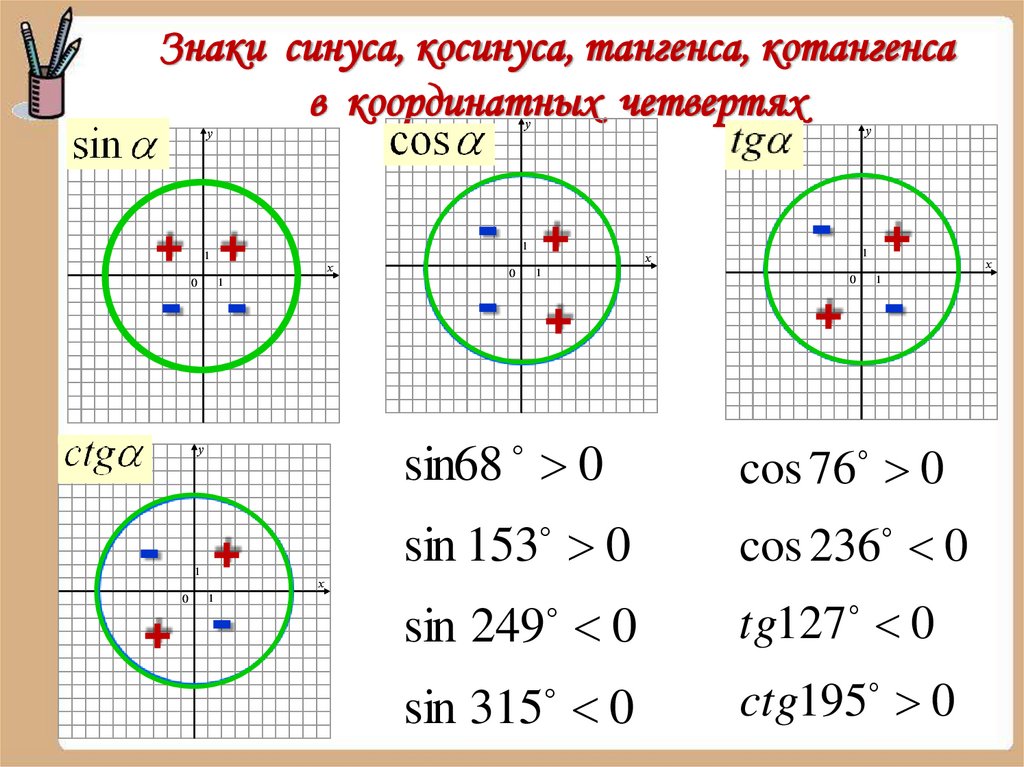
Знаки синуса, косинуса, тангенса, котангенса
в координатных четвертях
у
у
+ +
х
1
- -
0
1
- +
+ 1
1
х
- +
+ 1
1
0
sin68 0
cos 76 0
sin 153 0
cos 236 0
sin 249 0
tg127 0
sin 315 0
ctg195 0
у
0
- +
- +
1
1
0
у
х
х

19.

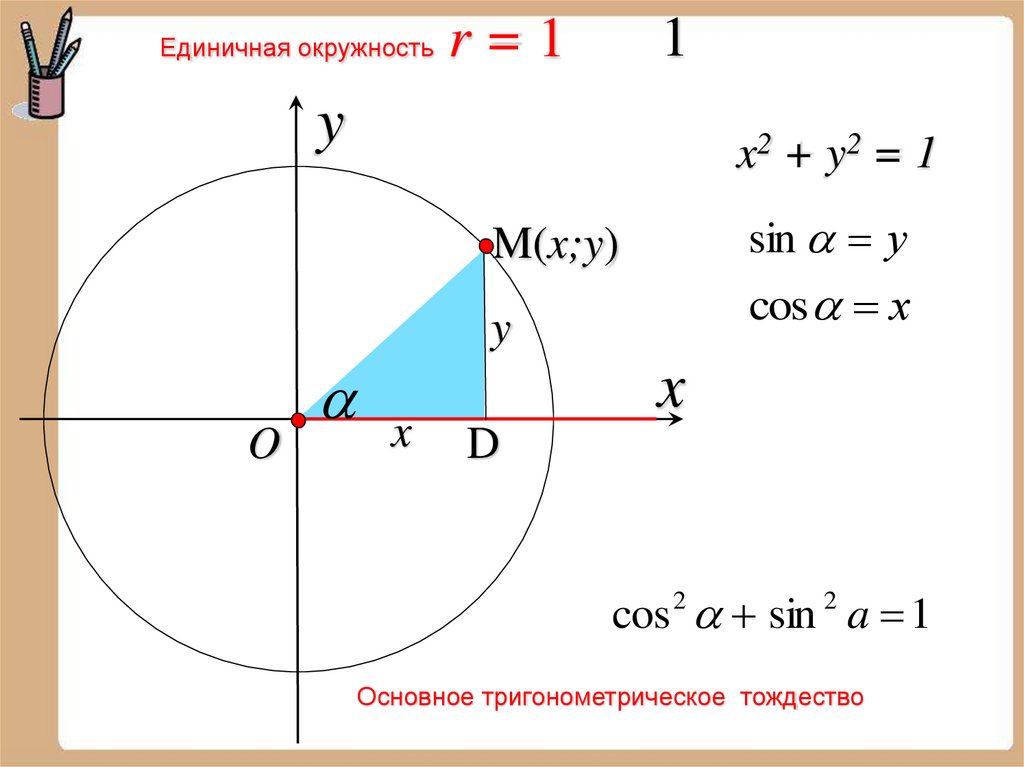
Единичная окружность
1
r=1
y
x2 + y2 = 1
sin у
M(x;y)
cos х
y
O
x
x
D
cos sin a 1
2
2
Основное тригонометрическое тождество

20.

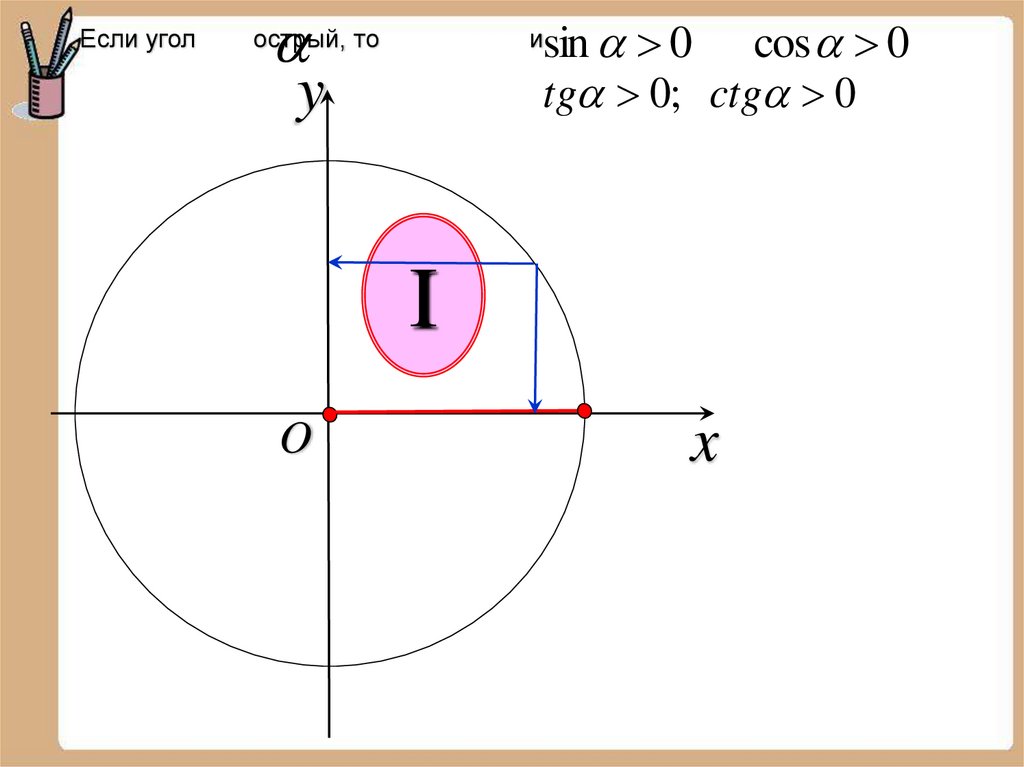
Если угол
y
sin 0 cos 0
tg 0; ctg 0
острый, то
и
I
O
x

21.

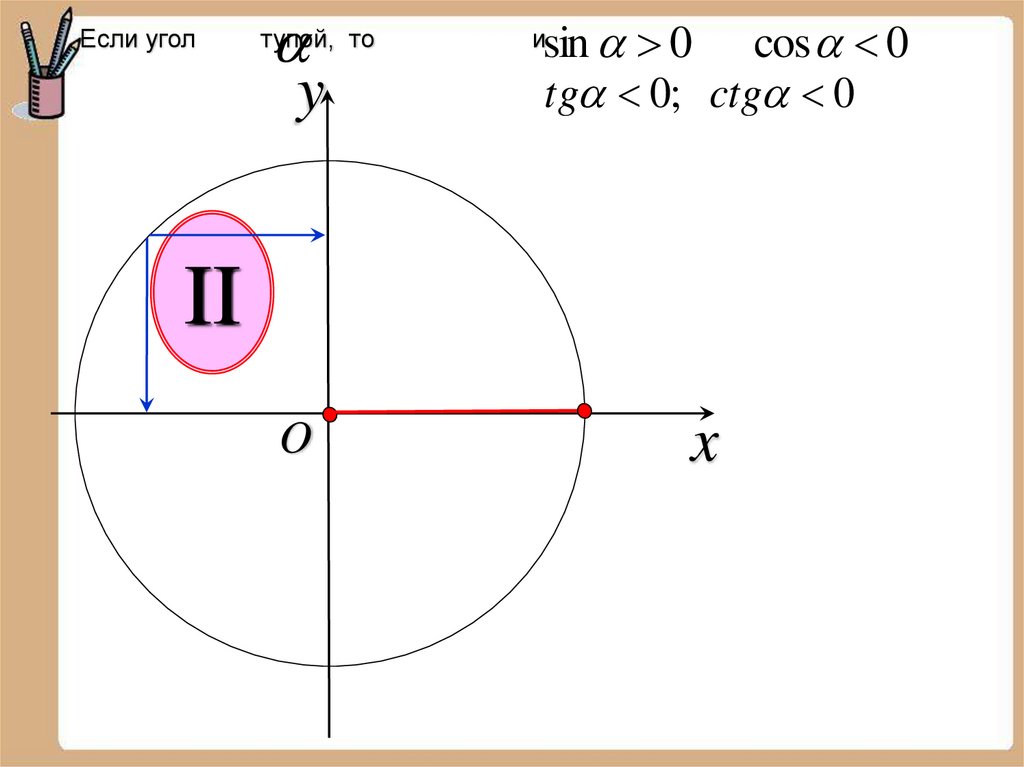
Если угол
y
тупой, то
sin 0 cos 0
tg 0; ctg 0
и
II
O
x

22.

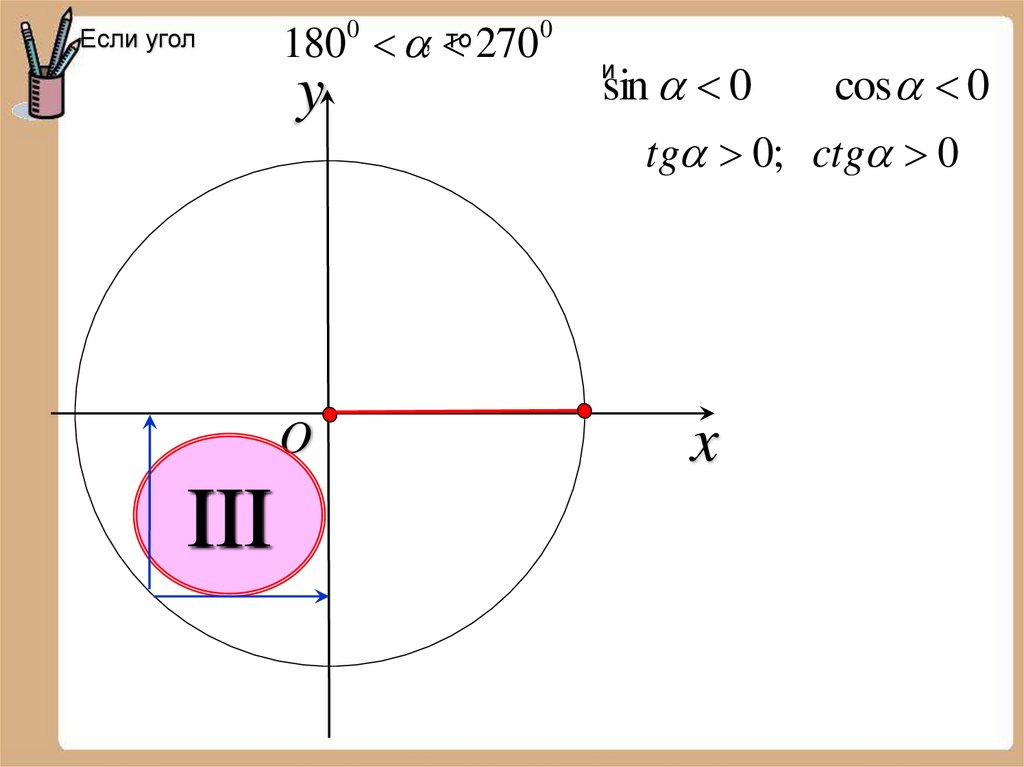
Если угол
180 270
0
y
O
III
, то
0
sin 0
cos 0
tg 0; ctg 0
и
x

23.

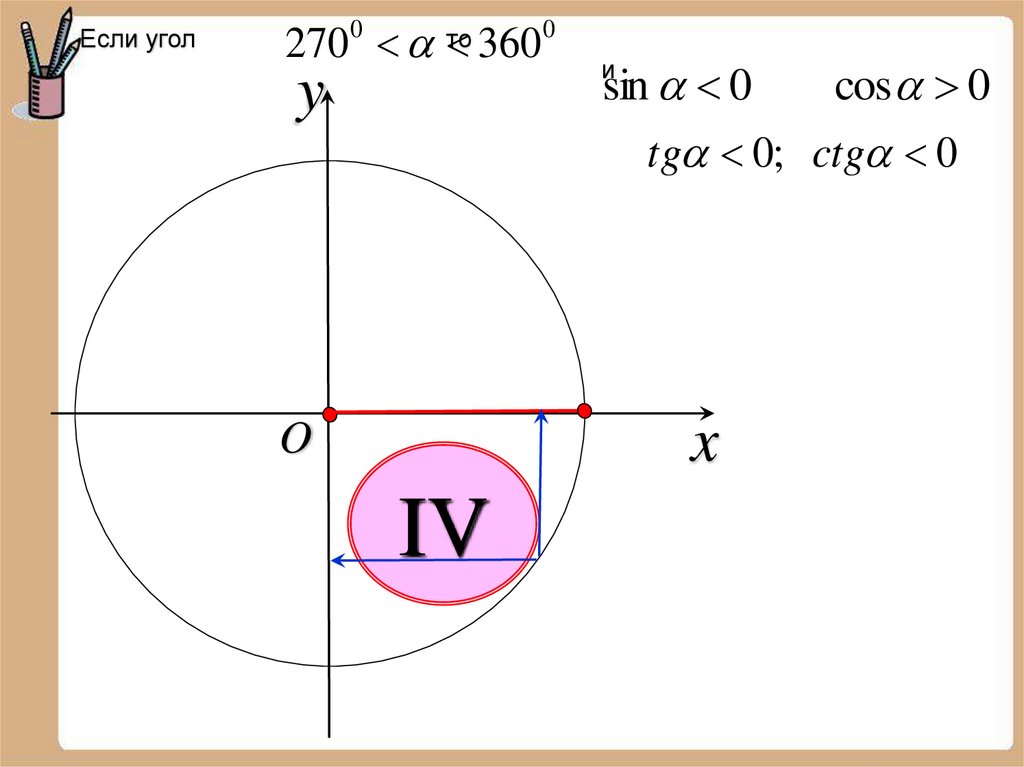
Если угол
270 360
0
, то
y
0
sin 0
cos 0
tg 0; ctg 0
и
x
O
IV

24.

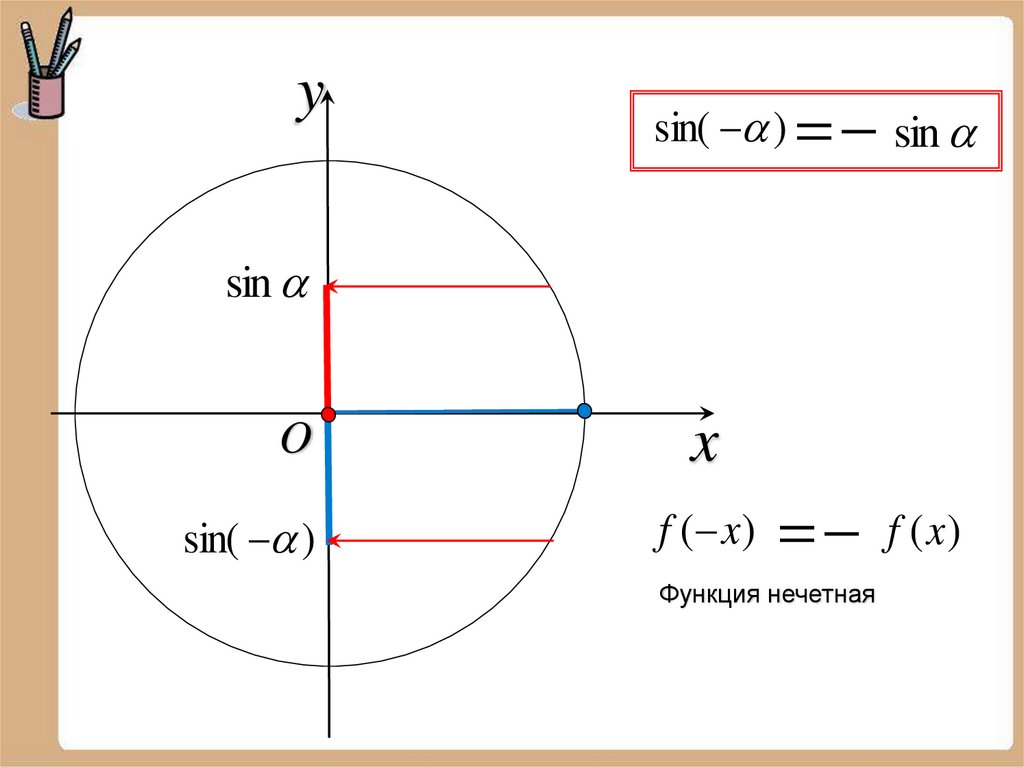
y
sin( ) sin
sin
O
sin( )
x
f ( x) f (x )
Функция нечетная

25.

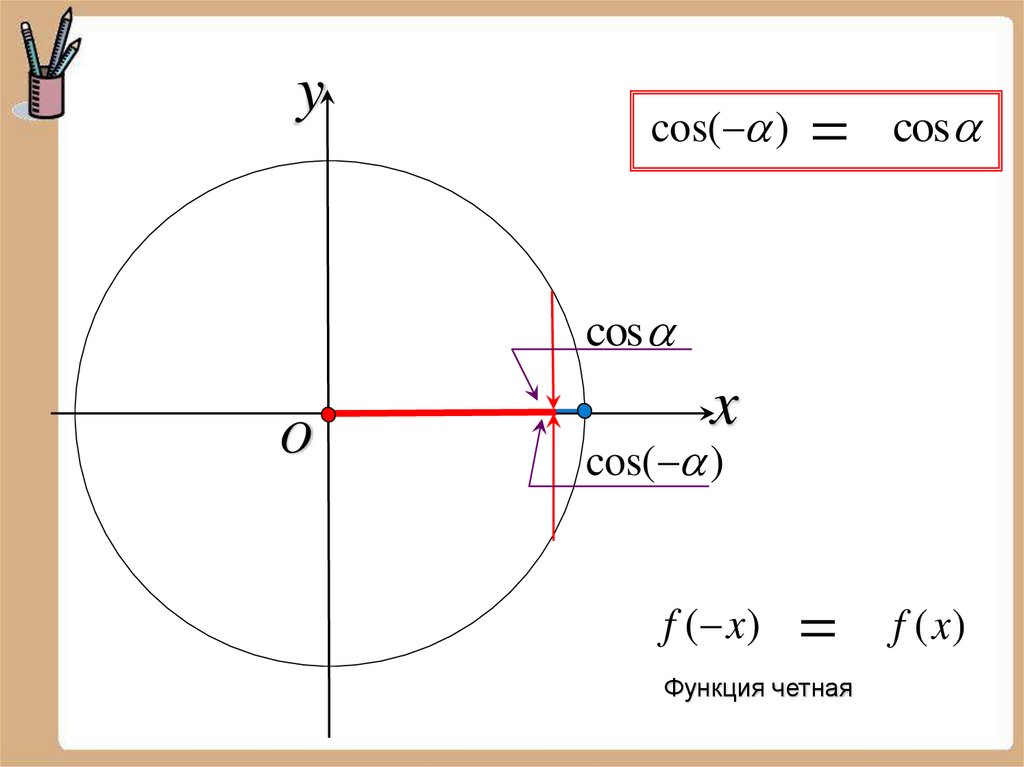
y
cos( )
cos
cos
O
x
cos( )
f ( x)
Функция четная
f (x )

26.

sin
tg
cos
sin
sin ( ) sin
tg( )
tg
cos
cos
cos( )
f ( x) f (x )
Функция нечетная
Докажи самостоятельно
tg( ) tg
ctg( ) ctg

27.

f ( x)
f (x )
Функция четная
cos( )
f ( x) f (x )
Функция нечетная
cos
sin( ) sin
tg( ) tg
ctg( ) ctg

28.

Четность, нечетность синуса, косинуса,
тангенса, котангенса
sin( ) sin
tg ( ) tg
ctg ( ) ctg
cos( ) cos
Нечетные функции
Четная функция

29.

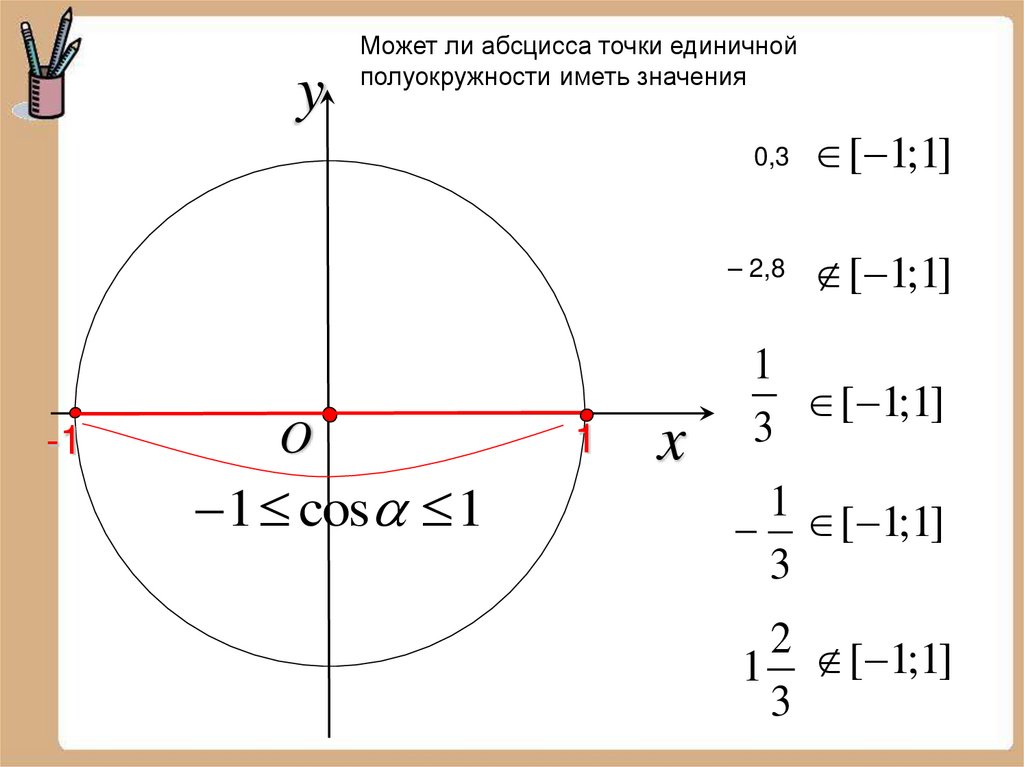
y
-1
Может ли абсцисса точки единичной
полуокружности иметь значения
O
1 cos 1
1
x
0,3
[ 1;1]
– 2,8
[ 1;1]
1
[ 1;1]
3
1 [ 1;1]
3
2 [ 1;1]
1
3

30.

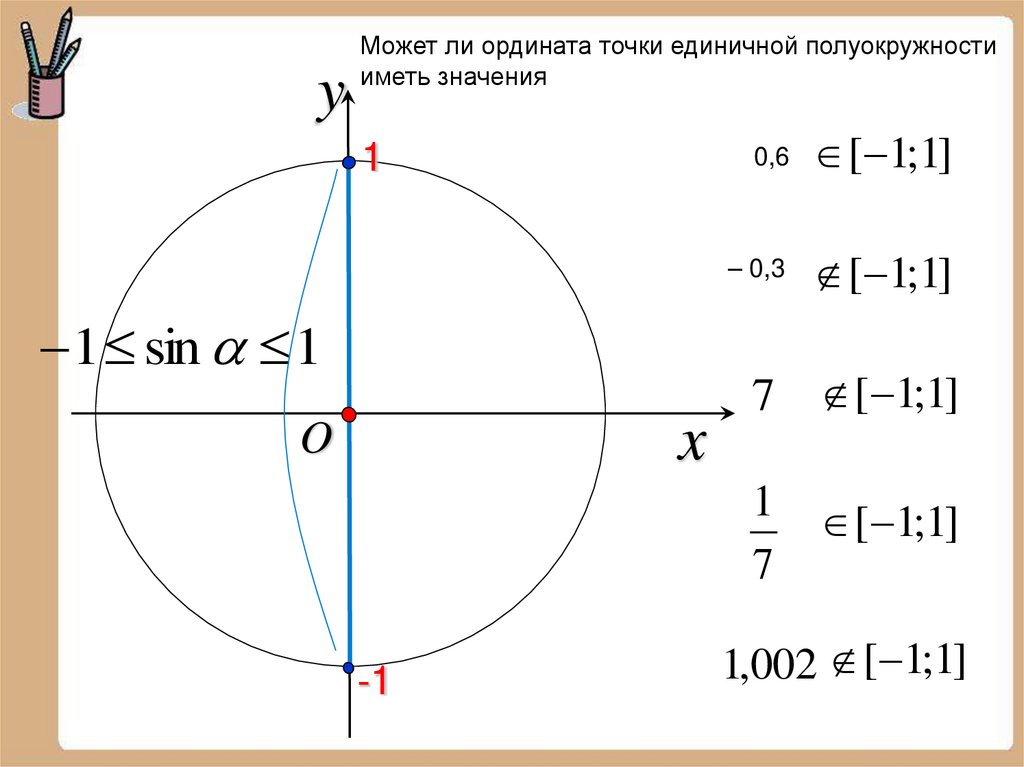
y
Может ли ордината точки единичной полуокружности
иметь значения
1
1 sin 1
x
O
0,6
[ 1;1]
– 0,3
[ 1;1]
7 [ 1;1]
1
7
-1
[ 1;1]
1,002 [ 1;1]

31.

Домашнее задание
Повторить определения синуса, косинуса,
тангенса и котангенса, таблицу значений
углов
и свойства четности и нечетности