Похожие презентации:
Тригонометрия – математическая дисциплина. Синус, косинус, тангенс и котангенс угла (10 класс)
1.
2.
Тригонометрия – математическая дисциплина, изучающаязависимость между сторонами и углами треугольника.
Тригонометрические вычисления применяются
практически во всех областях геометрии, физики
и инженерного дела, при измерении расстояний
до недалёких звёзд в астрономии, между
ориентирами в географии, при контроле системы
навигации, в теории музыки, акустике, оптике,
электронике, теории вероятностей, статистике,
биологии, медицине (включая ультразвуковое
исследование (УЗИ) и компьютерную
томографию), фармацевтике, химии,
сейсмологии, метеорологии, океанологии,
картографии, архитектуре, экономике,
электронной технике, машиностроении,
компьютерной графике.
3.
4.
Вспомним:0 90
с
а
a
sin
с
b
cos
c
a
tg
b
в
Синус острого угла в прямоугольном треугольнике —
отношение противолежащего катета к гипотенузе.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к
прилежащему.
5.
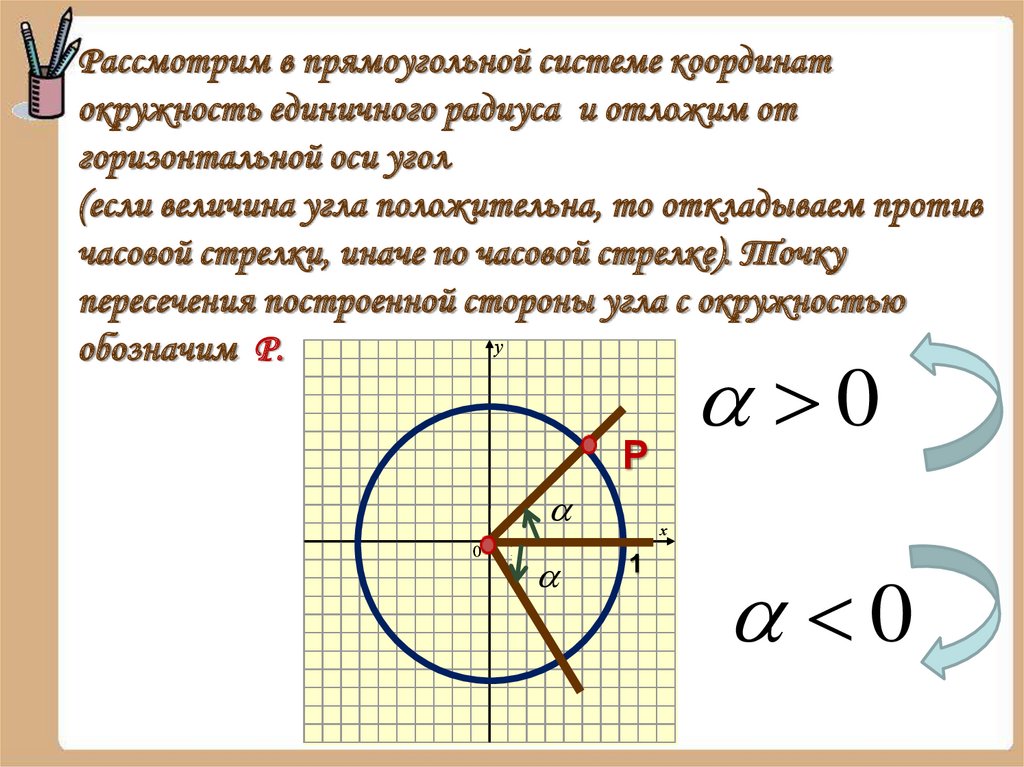
Рассмотрим в прямоугольной системе координатокружность единичного радиуса и отложим от
горизонтальной оси угол
(если величина угла положительна, то откладываем против
часовой стрелки, иначе по часовой стрелке). Точку
пересечения построенной стороны угла с окружностью
у
обозначим Р.
0
Р
1
0
1
х
1
0
6.
Р90у
Р60
Р45
Р30
Р180
Р
1
0
х 0
1
Р270
Р360
7.
Радианная мера углаR
С
центральный угол
R – радиус
С – длина дуги
Если R = C,
то центральный угол равен
одному радиану
Радианной мерой угла называется
отношение длины соответствующей дуги
к радиусу окружности
1 рад 57
8.
n180
180
n
n 60
4
60
180
3
60
3
180
180
180
n 4
45
4
4
45
4
9.
Самостоятельная работаВариант 1
1. Представьте угол 740о в виде ά° + 360°n
, где n – целое число,
0<ά<1800.
50о.
2. Точка Р – конечная точка поворота на
Найдите наименьшее по модулю значение
угла β, точки P1, которая получается из точки
Р симметрией относительно оси ординат.
3. Переведите угол
в радианную.
150о
из градусной меры
4. Переведите угол 1,25π из радианной
меры в градусную.
5. Допишите равенство ...0 =
6. Запишите формулу перехода от рад
к градусам.
7. Запишите, как найти через стороны
треугольника косинус угла ά. (рис)
Вариант 2
Представьте угол –710о в виде a° + 360°n,
где n – целое число, 0<ά<180°.
2. Точка Р – конечная точка поворота на
50о. Найдите наименьшее по модулю
значение угла β, точки P1 , которая
получается из точки Р симметрией
относительно оси абсцисс.
3. Переведите угол 135 о из градусной
меры в радианную.
4. Переведите угол 2,5π из радианной
меры в градусную.
5. Допишите равенство …0 =
6. Запишите формулу перехода от
радиан к градусам.
7. Запишите, как найти через стороны
треугольника синус угла ά.(рис)
10.
ОтветыВариант 1
№1
№2
№3
№4
№5
№6
№7
7400=3600·2+200
1300
2250
900
ά рад =
Вариант 2
№1
№2
№3
№4
№5
№6
№7
-7100 = 100 - 2·3600
-500
4500
450
ά0 =
рад
11.
cosу
1
P ( x; y)
у
sin
1
0
P (1;0)
х 0
1
х
1
12.
sin yСинус угла определяется как ордината
точки P
cos x
Косинус — абсцисса точки P
y
tg к абсциссе
Тангенс – отношение ординаты
x
точки P
x
Котангенс – отношение абсциссы
ctg к ординате
точки P
y
13.
Понятие синуса встречается уже в III в. до н. э.и имел название джива (тетева лука) ,
в IX в. заменено на арабское слово
джайб (выпуклость) , XII в. заменено на латинское
синус (изгиб, кривизна) .
Косинус – это дополнительный синус.
Тангенс переводится с латинского
как «касающийся»
14.
• В курсе геометрии вы познакомились с тангенсомострого угла, равным частному синуса и косинуса
этого угла:
tg φ = sin φ/cosφ
• С помощью этого равенства можно определить
тангенс любого угла φ, косинус которого отличен от
нуля.
• Тангенсом угла назывется частное синуса к
косинусу этого угла.
• Для углов, косинусы которых равны 0, т. е. углов
вида π/2 + πn (n – любое число), тангенс не
существует.
15.
• На рисунке к единичной окружности вточке P0 проведена касательная; Pφ –
конечная точка поворота на угол φ; C –
точка пересечения касательной и
прямой OP φ.
• Ордината точки С равна тангенсу угла
φ
16.
Докажем это. Заметимсначала, что tg φ и
ордната точки С
одинаковы по знаку. Так,
если Pφ – точка I или III
координатной четверти,
то sin φ и cosφ или оба
положительны…
• или оба
отрицательны.
17.
• Значит, их частное tg φ положительное. Точка С вэтих случаях расположена в верхней полуплоскости
и, следовательно, имеет положительную ординату.
• Если же точка Pφ находится во II или в IV
координатной четверти, то знаки sin φ и cosφ
различны, следовательно, tg φ отрицателен. Точка
С при этом находится в нижней полуплоскости и
имеет отрицательную ординату.
18.
Р90у
Р60
1
Р45
sin
45
0,7
Р30
cos45 0,7
1
2
-1
1
sin 30
2
cos 30 0,9
Р180
Р
1
0
х 0
1
1
2
1
Р360
sin 60 0,9
1
cos 60
2
-1
Р270
19.
Запомним !cos
tg
ctg
45
60
1
2
2
2
3
2
3
2
2
2
1
2
30
sin
1
3
3
3
3
1
3
1
1
3
3
3
20.
Р90у
Р0 (1; 0)
Р90 (0; 1)
Р180
Р
1
0
х 0
1
Р360
Р180 (-1; 0)
Р270
Р270 (0;-1)
21.
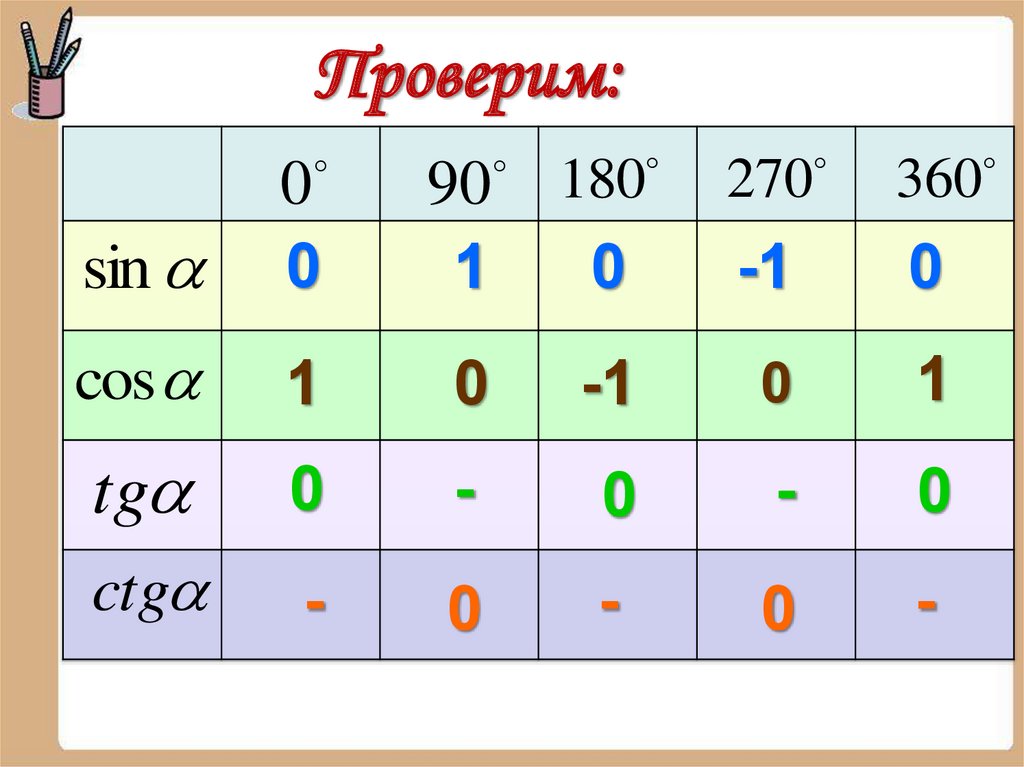
Проверим:180
270
0
-1
0
0
-1
0
1
0
-
0
-
0
-
0
-
0
-
sin
0
0
90
1
cos
1
tg
ctg
360
22.
Знаки синуса, косинуса, тангенса, котангенсав координатных четвертях
у
у
+ +
х
1
- у
0
1
1
1
- +
+ 1
1
0
cos 76 0
sin 153 0
cos 236 0
sin 249 0
tg127 0
sin 315 0
ctg195 0
х
х
sin68 0
- +
+ 0
- +
- +
1
1
0
у
х
23.
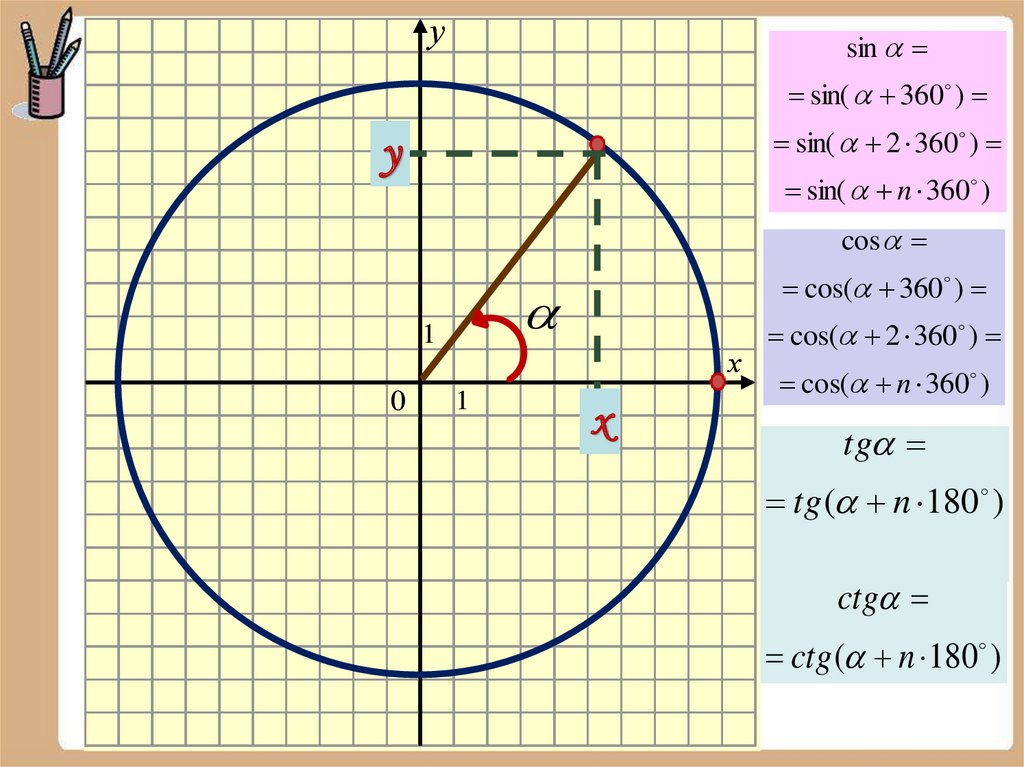
Периодичность тригонометрическихфункций
При изменении угла на целое число оборотов
значения синуса, косинуса, тангенса, котангенса
не изменяются
24.
уsin
sin( 360 )
sin( 2 360 )
у
sin( n 360 )
cos
1
0
cos( 360 )
х
1
х
cos( 2 360 )
cos( n 360 )
tg
tg ( n 180 )
ctg
ctg ( n 180 )
25.
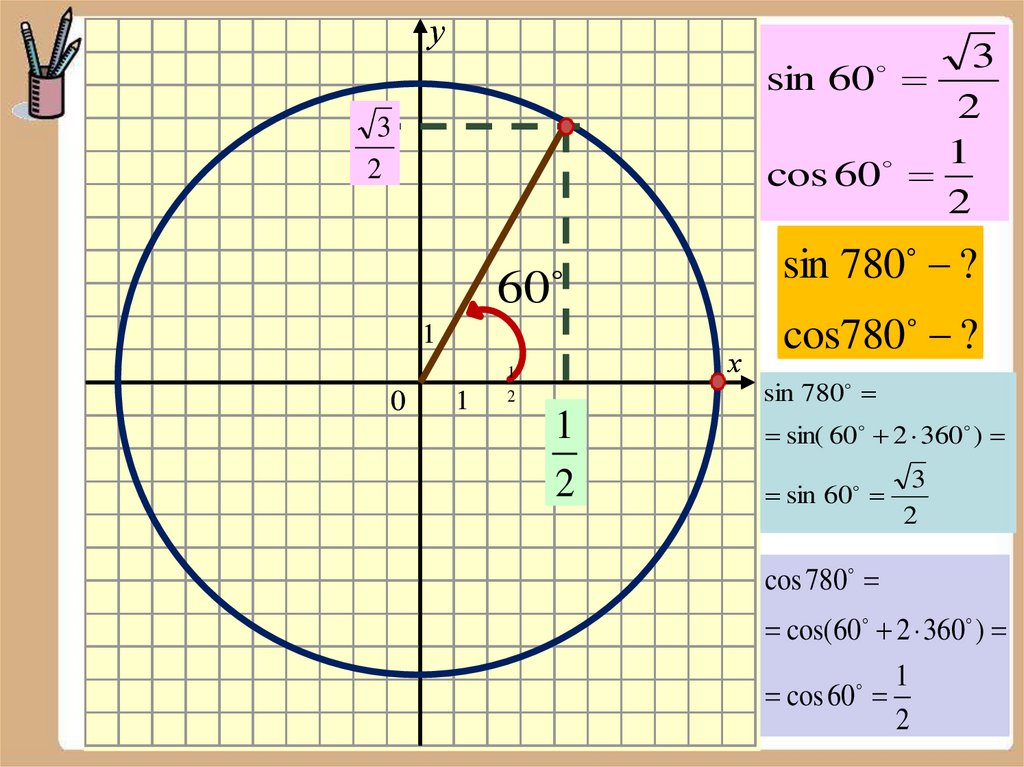
у3
sin 60
2
1
cos 60
2
3
2
60
1
0
1
420 ?
sin 780
х
1
2
1
2
cos420
cos780 ?
sin
sin 780
420
sin( 60
2 360 )
sin( 60 360 )
sin 60
sin 60
3
2 23
cos 780
cos
420
360 ))
cos(
cos(60
60 2360
11
cos
60
cos 60
22
26.
sin 765cos 1110
sin( 45 2 360 )
cos(30 3 360 )
2
sin 45
2
3
cos 30
2
1
sin( 1470 ) sin 1470 sin( 30 4 360 ) sin 30
2
1
cos( 1140 ) cos1140 cos(60 3 360 ) cos 60
2
sin( 810 ) sin 810 sin( 90 2 360 ) sin 90 1
cos( 1170 ) cos1170 cos(90 3 360 ) cos 90 0
27.
sin( ) sin4
4
2
2
sin 2,5 sin( 0,5 2 ) sin 0,5 sin
2
1
9
1
2
cos( ) cos( 2 ) cos( 2 ) cos 4
4
4
4
2
13
1
3
tg
tg (2 ) tg ( 2 ) tg
6
6
6
6
3
7
1
ctg ( ) ctg (2 ) ctg ( 2 ) ctg 3
3
3
3
3
28.
Домашнее задание№6.3 А(1-5), Б(1-5), В(1-5)
29.
• Спасибо за внимание!Спасибо за внимание!






















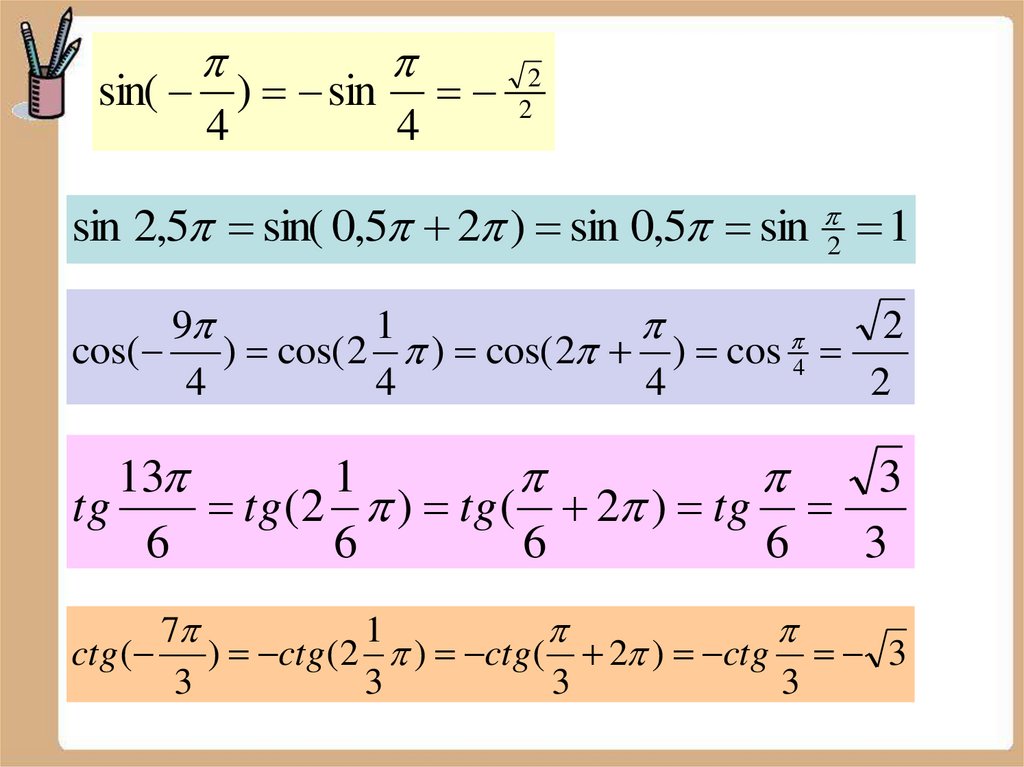


 Математика
Математика








