Скорость и ускорение материальной точки

1. СКОРОСТЬ И УСКОРЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ

ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
КИНЕМАТИКА
ЛЕКЦИЯ 1

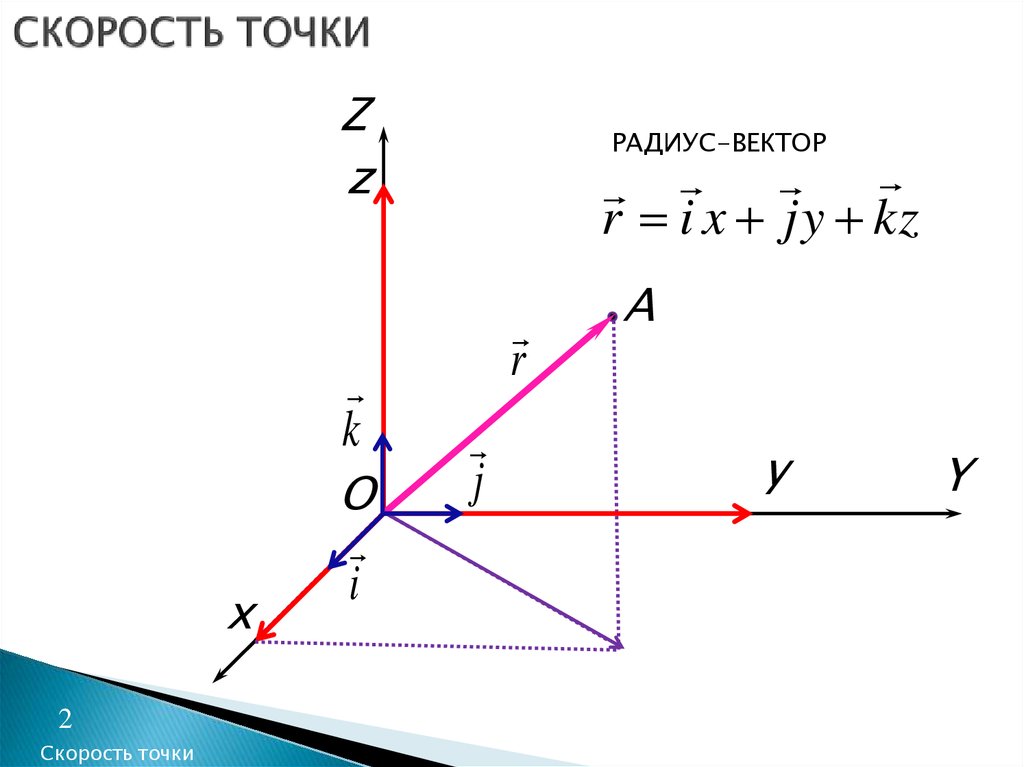
2. СКОРОСТЬ ТОЧКИ

Z
z
k
х
2
Скорость точки
O
i
РАДИУС-ВЕКТОР
r i x jy kz
r
j
A
y
Y

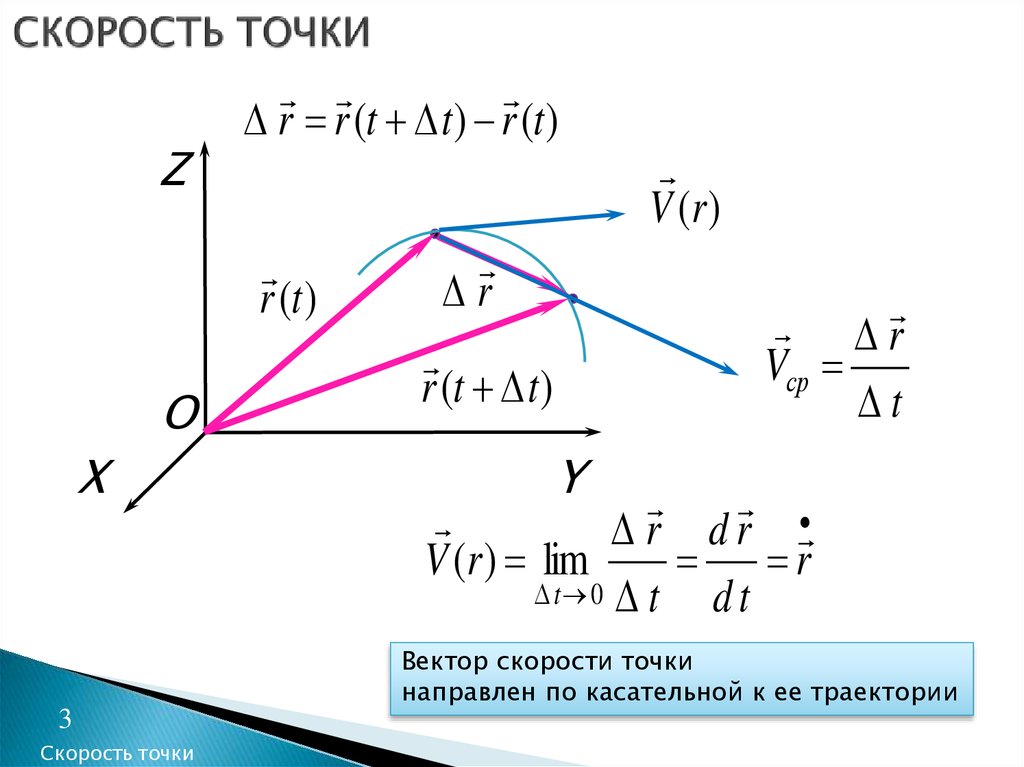
3. СКОРОСТЬ ТОЧКИ

Z
r r (t t ) r (t )
r (t )
O
X
r
V (r )
r
Vср
t
r (t t )
Y
r dr
V (r ) lim
r
t 0 t
dt
Вектор скорости точки
направлен по касательной к ее траектории
3
Скорость точки

4. СКОРОСТЬ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ЕЕ ДВИЖЕНИЯ

dx dy dz
dr
d
j
k
V (t )
i x jy kz i
dt
dt
dt
dt
dt
V x x
V y y
V z z
4
Скорость точки
V (r ) i v x j v y k v z
V
2
Vx
2
Vy
2
Vz
2
2
2
x y z

5. СКОРОСТЬ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ. ПРИМЕР

Движение точки задано уравнением
t
t
r 2 cos i 2 sin j
6
6
Определить уравнение траектории и скорость точки при t = 1c.
t
x(t ) 2 cos ,
6
t
y(t ) 2 sin
6
2
2
t
t
x
y
сos2 sin 2
1
4
6
6 4
x2 y2
1
4
4
5
Скорость точки
уравнение траектории
(окружность)

6. СКОРОСТЬ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ. ПРИМЕР

Движение точки задано уравнением
t
t
r 2 cos i 2 sin j
6
6
Определить уравнение траектории и скорость точки при t = 1c.
t
Vx x sin ,
3 6
Vx (1) 0,52 м / с
t
Vy y cos
3
6
Vy (1) 0,91м / с
y
V
2
Vx
2
Vy
V
1,1м / с
1
6
Скорость точки
2
x

7. СКОРОСТЬ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ЕЕ ДВИЖЕНИЯ

dr dr ds ds
V
s
dt ds dt dt
dr
ds
r
ds
V (t )
dt
Вектор скорости точки направлен по касательной к ее траектории
7
Скорость точки

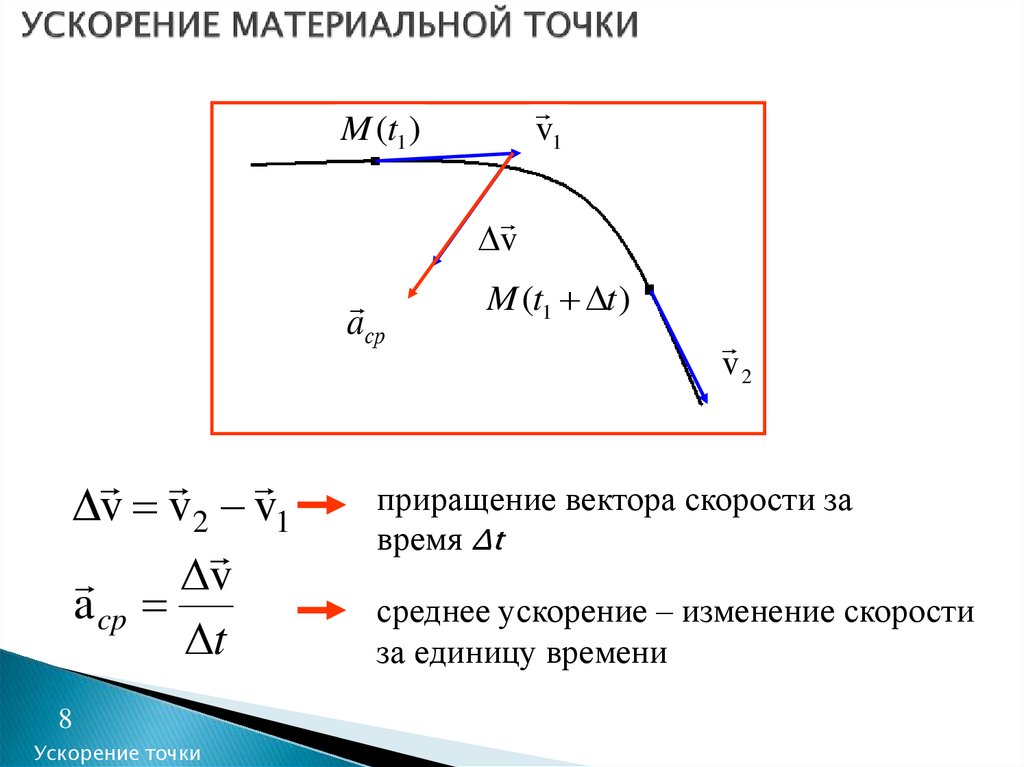
8. УСКОРЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ

v1
M (t1 )
v
aср
v v2 v1
v
a cp8
t
8
Ускорение точки
M (t1 t )
v2
приращение вектора скорости за
время Δt
среднее ускорение – изменение скорости
за единицу времени

9. УСКОРЕНИЕ ТОЧКИ ПРИ ВЕКТОРНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ

a cp
v
t
v
d v d 2r
a lim
2
t
dt
dt
t 0
ускорение в данный момент
времени t
Ускорение точки — это векторная величина,
характеризующая быстроту изменения ее скорости и равная
первой производной от скорости или второй производной
от радиус-вектора по времени
9
Ускорение точки

10. УСКОРЕНИЕ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ

в декартовой системе координат
вектор скорости
v
вектор ускорения
a
vx i v y j vzk
a x i a y j a zk
d v
v x i v y j v z k
a x i a y j a zk
dt
a x v x x
a y v y y
a z v z z
a | a | a 2x a 2y a 2z
10
Ускорение точки

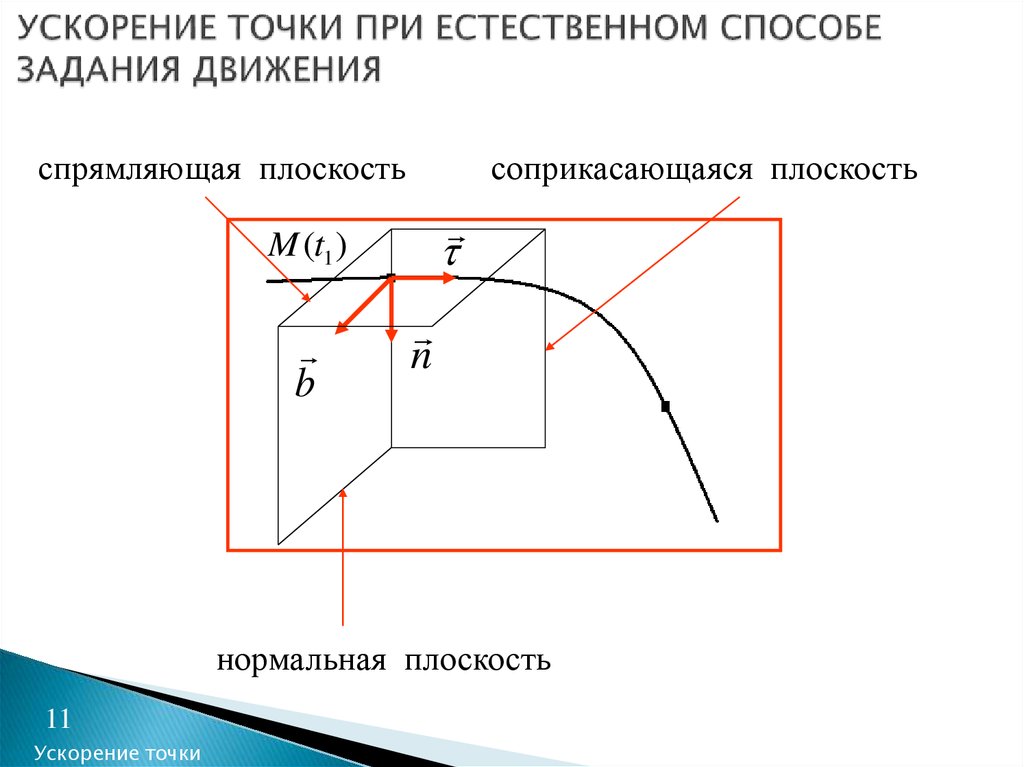
11. УСКОРЕНИЕ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ

спрямляющая плоскость
соприкасающаяся плоскость
M (t1 )
b
n
нормальная плоскость
11
Ускорение точки

12. УСКОРЕНИЕ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ

dv d
d
a
s s s
dt dt
dt
Момент времени
t
1
c
d
v
dt
2
Момент времени
Ускорение точки
d
dt
12
t+∆t
t
d d
n
dt
dt
2 1

13. УСКОРЕНИЕ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ

d
lim
t 0 t
dt
При малых ∆φ
d
a s s
dt
1
sin / 2 / 2
d
2 sin / 2
lim
t 0
t
dt
2
lim
t 0 t
a s s n a ann a an
Касательное ускорение
13
Ускорение точки
Нормальное ускорение

14. УСКОРЕНИЕ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ

M
ds
d
2
2
d
d ds
d
s
v
s
s
s 2
dt
ds
ds dt
угловая скорость вектора
Радиус кривизны
траектории
d 1
ds
ds d
Ускорение точки
s
v
2
2
a a an v n
14
v
an
a
2
a an
2
v2
2

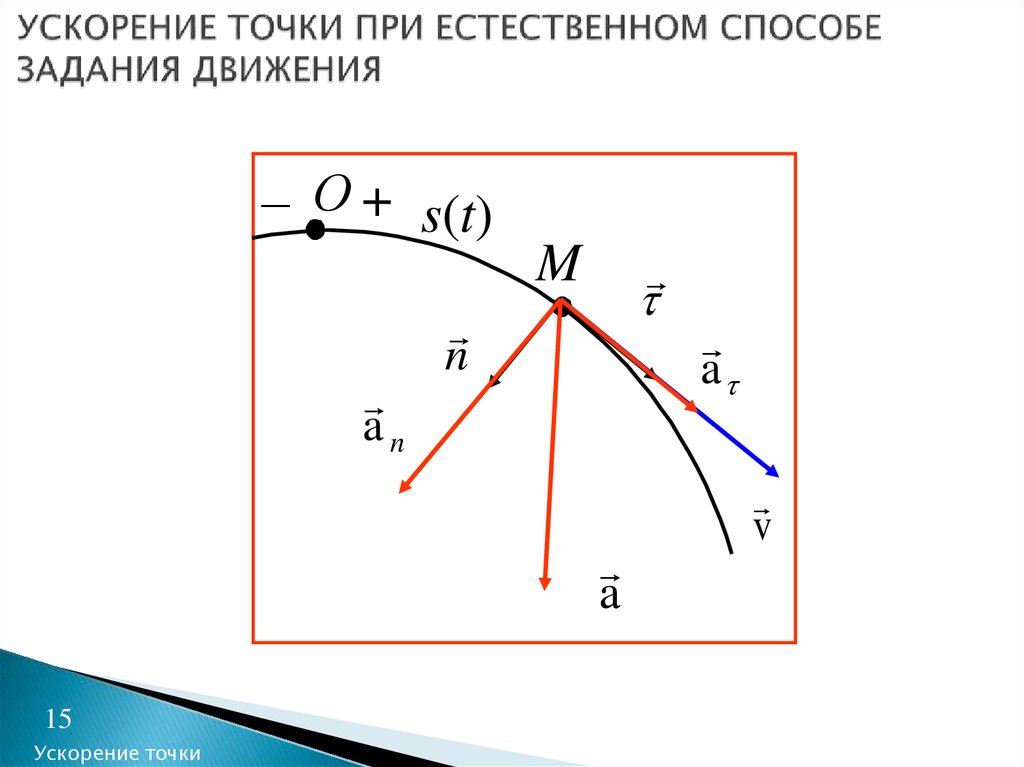
15. УСКОРЕНИЕ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ

– О + s(t)
M
an
n
a
15
Ускорение точки
a
v

16. ПРОЕКЦИИ СКОРОСТИ И УСКОРЕНИЯ НА ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА

b
n
v v vn n vbb
v s
vn 0
16
Ускорение точки
vb 0
a a an n abb
a s a s 2
n
ab 0

17. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТОЧКИ

a 0
v const
v t1
v t1 v t2 v t3
v t 2
v t3
Такое движение называется равномерным
Равнопеременное движение
a const
Ускоренное движения:
v a 0
Замедленное движения:
v a 0
v 0
a 0
a 0
17
Ускорение точки
v 0