Похожие презентации:
Модель свободных электронов
1.
Модель свободных электронов-наиболее слабо связанные электроны в металлах довольно свободно
перемещаются в объеме кристаллической решетки.
-мы пренебрегаем взаимодействием валентных электронов с ионными
остовами и ведем расчеты так, как если бы электроны могли без всяких
ограничений перемещаться по образцу.
-полную энергию можно считать равной кинетической, а потенциальной
энергией можно пренебречь.
10 8 10 9
1) электроны проводимости не отклоняются ионами, так как последние
расположены в узлах кристаллической решетки, в которой электронная волна
распространяется свободно, как во всякой периодической структуре;
2) электроны проводимости лишь редко испытывают рассеяние на других
электронах проводимости. Это свойство следствие принципа Паули.
Газ свободных, невзаимодействующих электронов, подчиняющихся принципу
Паули, называется сводным электронным газом Ферми.
2.
Энергетические уровни в одномерном случаеРассмотрим поведение газа свободных электронов на основе квантовой теории и
принципа Паули. Пусть электрон массой m движется в бесконечно глубокой
потенциальной яме длиной L . Волновая функция электрона n определяется
решением уравнения Шредингера
H n n
. Так как потенциальной энергией пренебрегаем, то гамильтониан
H p 2 / 2m
, р - импульс электрона. В квантовой механике импульс есть оператор
d
p i
dx
, так что
n-
2 d 2 n ( x)
H n
n n
2
2m dx
(1)
энергия электрона в состоянии n , описываемом волновой функцией n
(орбиталью)
3.
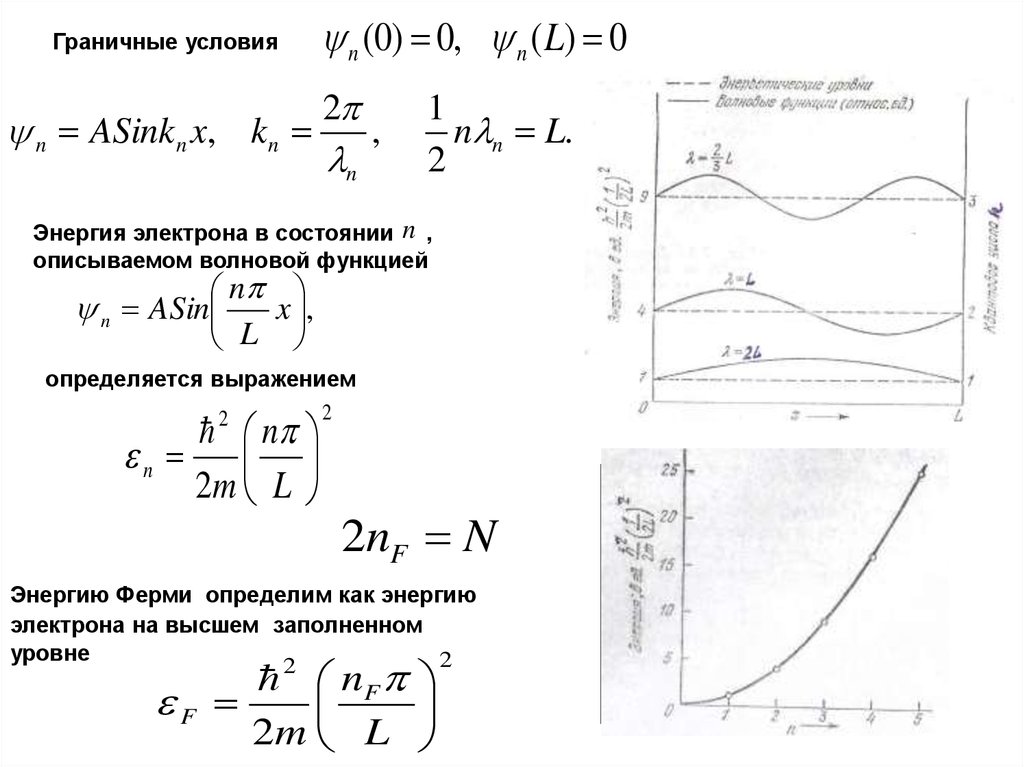
Граничные условияn ASink n x, k n
n (0) 0, n ( L) 0
2
n
,
1
n n L.
2
Энергия электрона в состоянии n ,
описываемом волновой функцией
n
n ASin
x ,
L
определяется выражением
2
2
n
n
2m L
2nF N
Энергию Ферми определим как энергию
электрона на высшем заполненном
уровне
2
2
F
F
n
2m L
4.
Функция распределения Ферми-ДиракаФункция распределения Ферми-Дирака есть вероятность того, что
одночастичное состояние с энергией является занятым,
когда система частиц, для которых указанное состояние – одно из
возможных, находится в тепловом равновесии при температуре T .
Воспользуемся распределением Гиббса: вероятность того, что система
содержит N частиц и ее полная энергия равна n пропорциональна
P( N , n ) ~ exp[( N n ) / k BT ] .
Здесь - химический потенциал.
Если состояние занято, то в случае одного электрона
P(1, n ) ~ exp[( n ) / k BT ] .
Если состояние не занято, то энергия равна нулю
P(0,0) ~ exp 0 1 .
5.
expk BT
P(1, )
1
f ( )
P(0,0) P(1, )
exp
1
1 exp
k BT
k BT
функция ФермиДирака
1
f ( )
1
exp
k BT
6.
В каждой конкретной задаче химический потенциал определяется изусловия постоянства полного числа электронов в системе, равного N :
f ( ) N ,
i
или в интегральной форме
i
f ( ) D( )d N ,
где
D( )
0
плотность состояний.
При абсолютном нуле F , так что в пределе при T 0 функция f ( )
изменяется скачком от значения равного единице (заполненный уровень), до
значения 0 (вакантный уровень) при F . При любой температуре
T 0 при функция f ( ) =1/2.
F
F
T 0
F
7.
Свободный электронный газ в трехмерном случаеУравнение Шредингера для свободной частицы в трехмерном случае
имеет вид:
2 2
2
2
2 2 2
2m x
y
z
k (r ) k k (r )
Если электроны заключены в ограниченном объеме, имеющем форму
куба со стороной L , то решением уравнения будет функция
nx n y nz
x Sin
y Sin
z
L
L
L
k (r ) ASin
Волновая функция, удовлетворяющая уравнению Шредингера
для свободной частицы с периодическими граничными условиями
( x, y, z ) ( x L, y, z ) ( x, y L, z ) ( x, y, z L)
ik r
представляет собой бегущую плоскую волну: k (r ) e
при условии, что компоненты волнового вектора принимают следующий
набор значений k x , k y , k z 0;
2
4
;
;…
L
L
Собственные значения энергии в состоянии с волновым вектором k :
2 2 2 2
k
k
(k x k y2 k z2 )
2m
2m
8.
Свободный электронный газ в трехмерном случаеd
Если оператором импульса p i , подействовать на волновую
dx
функцию k (r ) , то получим
p k (r ) i k (r ) k k (r )
k / m
Основное состояние системы из N свободных электронов можно описать
точками внутри сферы в k - пространстве.
Волновые векторы,
упирающиеся в поверхность этой сферы, имеют
длины, равные k F , а энергия, соответствующая энергии этой сферы,
является энергией Ферми
2
F
2
kF
2m
Из возможного набора волновых векторов k следует, что каждой тройке
квантовых чисел k x , k y , k z отвечает элемент объема в k- пространстве
3
3
величиной (2 / L) . Поэтому в сфере объемом 4 k F / 3 число точек,
описывающих разрешенные состояния, равно числу ячеек объемом ( 2
и поэтому число разрешенных состояний равно
4 k F3 / 3
V 3
2
kF N
3
2
(2 / L)
3
/ L, ) 3
9.
Свободный электронный газ в трехмерном случае3 2 N
Радиус сферы зависит лишь от концентрации электронов k F
V
2
/
3
2
2
3
N
Энергия Ферми равна
F
2m V
3 2 N
Скорость электронов на поверхности Ферми F
m V
1/ 3
1/ 3
Полное число состояний с энергией F равно
V 2m
N 2 2F
3
3/ 2
Плотность состояний при энергии Ферми
dN
V 2m
D( F )
d F 2 2 2
3/ 2
Выражение для плотности состояний можно получить в более простой форме
dN 3 N
D( F )
d F 2 F
Если исходить из общего выражения для (k ) и действовать по
аналогии с расчетом, примененном при выводе плотности состояний
для фононов, то D( ) можно записать в виде
2V
D( )
(2 )3
dS
grad k
1F/ 2
10.
Теплоемкость электронного газаСV С g Сe
3
kB
2
1
k BT
2
3
k BT
2
3
3
E N A k BT RT
2
2
3
СV 3R R
2
кл
e
3
С R
2
кл
e
Обратившись к функции плотности состояний D( ) ,
можно качественно объяснить теплоемкость
электронного газа Ферми.
Испытывают тепловое возбуждение и приобретают
энергию ~ kBT лишь электроны, находящиеся в
состояниях с энергией в интервале k T вблизи уровня
B
Ферми.
11.
Тепловое возбуждение при повышении температурыот 0 до T может испытать только часть электронов порядка отношения
T / TF.
T
Число электронов, испытывающих тепловое возбуждение, равно N N
TF
Каждый из NT / TF электронов обладает избыточной тепловой энергией порядка kBT
, а полная энергия теплового возбуждения электронов составляет величину
порядка
NT
E
k BT
TF
Теплоемкость электронного газа равна
E
T
Сe
Nk B
T
TF
Таким образом электронная теплоемкость ~ T ; при комнатной
температуре Сe много меньше значения
теория, примерно в 100 раз.
3
Nk B , которое дает классическая
2
12.
kBT FТеплоемкость электронного газа
Полное изменение энергии системы электронов представим в виде двух частей:
F
N f ( ) D( )d
E f ( ) D( )d D( )d
0
0
0
F N F f ( ) D( )d
0
Теплоемкость электронного газа
E
f
Сe
D( )
d
T
T
0
N
f
0 F
F D( )
d
T
T
0
Сe ( F ) D( )
0
f ( )
d
T
При низких температурах ( kBT / F 0,01 ), для которых и ведется
рассмотрение, производная f ( ) / T велика только при энергиях
близких к F , и поэтому вместо функции D( ) можно взять ее значение
при F и вынести ее из под знака интеграла; в результате получим:
Сe D( F ) ( F )
0
f ( )
d
T
13.
Теплоемкость электронного газаВ приближении первого порядка по температуре в выражении для функции
распределения Ферми - Дирака химический потенциал можно заменить
постоянной величиной F (0) .
F
exp
k BT
f ( ) F
T
k BT 2
F
exp
k BT
x F / k BT
1
2
ex
Сe D( F )k T x
dx
x
2
(e 1)
F / k BT
2
B
ex
2
x (e x 1) 2 dx 3
2
Для свободного электронного газа
получим выражение
Сe D( F )k T
2
B
D( F )
2
2
1
2 D( F )k B2T
3 3
dN 3 N
, для теплоемкости
d F 2 F
1 2
k BT 1 2
T
Сe Nk B
Nk B
2
k BTF 2
TF
14.
1 2T
Nk B
Сe
2
TF 1 2 T 1 2 k BT
кл
3
Сe
3
TF 3
F
kB N A
2
Так как электронный газ в металлах является вырожденным, термическому
возбуждению даже в области высоких температур подвергается лишь
незначительная доля свободных электронов (~ 1%); остальные электроны
энергию не поглощают.
3
Теплоемкость решетки с понижением температуры падает ~ T и вблизи
абсолютного нуля может оказаться столь малой, что основное значение может
приобрести Сe , которая с понижением температуры падает значительно
медленнее ( Сe ~ T ).
15.
Экспериментальные данные по электронной теплоемкости металловC AT BT 3
CV / T A BT 2
16.
Электропроводность и закон ОмаE
F
На электрон в электрическом поле
и магнитном поле B действует сила
,
1 , поэтому уравнение движения электрона имеет вид
равная
e( E B )
c
1
d
dk
F m
e( E B )
dt
dt.
c
В отсутствие столкновений внешнее электрическое поле однородно смещает все
точки сферы Ферми в к-пространстве.
t
Под действием постоянной силы , действующей в течение промежутка времени
,каждый электрон с волновым вектором k получает приращение k F t ./
Это эквивалентно смещению сферы
Ферми, как целого, на расстояние k .
Теперь полный импульс равен N k (до включения поля суммарный импульс
электронов был равен нулю).
Включение постоянного внешнего поля увеличивает энергию системы на
величину N ( k ) 2 / 2m .
eE
Интегрируя верхнее выражение при B = 0, получим: k (t ) k (0)
t
k . eE t /
17.
18.
Если среднее время между столкновениями равно, то стационарное
в данном
поле смещение сферы Ферми k равно:
k eE / .
Для приращения скорости имеем:
eE / m
Если в единице объема мы имеем n электронов, каждый с зарядом q=-e, то в
постоянном электрическом поле E плотность тока, вызванного полем , равна
2
j nq ne E / m
Это выражение имеет форму закона Ома:
j E
следовательно, имеем для :
ne 2 / m
Удельное сопротивление есть величина, обратная электропроводности, т.е.
1
m
2
ne
Средняя длина свободного пробега электронов проводимости
l F
19.
Экспериментальные данные об электросопротивлении металловЭлектросопротивление большинства металлов при комнатных температурах
обусловлено в основном столкновениями электронов проводимости с
решеточными фононами, а при температуре жидкого гелия – столкновениями с
примесными атомами и дефектами решетки.
g i
Если концентрация примесных атомов мала, то i не зависит от температуры
(правило Матиссена).
Результаты измерений трех образцов Na:
остаточное сопротивление меняется от
образца к образцу, тогда как
сопротивление, обусловленное
тепловым движением атомов решетки, не
зависит от образца.
Фононный вклад в g в металлах:
при высоких температурах g ~ T ,
при T D
g ~ T 5.
20.
Теплопроводность металловКоэффициент теплопроводности газов
Теплопроводность газа Ферми
1
3
СV l
1
2
F m F2
2 nk B2T
2 nk B2T
e
F l
2
3 m F
3m
В чистых металлах теплопроводность обусловлена в основном
электронами при любых температурах. В металлах с примесями, а также
неупорядоченных сплавах вклад фононов в теплопроводность может
быть сравним с вкладом электронов.
Закон Видемана-Франца
Для металлов при не очень низких температурах отношение
коэффициента теплопроводности к удельной электрической
проводимости прямо пропорционален ~ T .
2 nk B2T
2 kB
T
2
3mne / m 3 e
2
число Лоренца
2 kB
L
T
3 e
2
21.
Свободный электронный газ во внешних поляхСтатическая
реакция
электронного
газа
сводится
к
электростатическому
экранированию
кулоновского
взаимодействия.
Динамическая реакция электронного газа проявляется в типичном для
металлов отражении света и в возбуждении плазмонов – форме
коллективного движения электронного газа.
Уравнение Максвелла, учитывающие диэлектрическую реакцию среды,
записывается в виде
D
rot H E
,
t
D
где D - электростатическая индукция ( D 0 E P ); rot H E ,
t
(3.1)
P -
поляризация (дипольный электрический момент единицы объема). Первое
слагаемое
E обусловлено
смещением
смещением связанных зарядов.
свободных
электронов,
D
t
-
22. Свободный электронный газ во внешних полях
Диэлектрическая функция свободного электронного газаУравнение движения свободного электрона в электрическом поле
Если x и
d 2x
m 2 eE
dt
E периодические функции времени
x
Дипольный момент электрона
e i t, получим
eE
m 2
e2 E
p ex
m 2
ne 2 E
Поляризация (дипольный момент единицы объема) P nex
m 2
Диэлектрическая функция при частоте
D( )
P
( )
1
0 E ( )
0 E ( )
Диэлектрическая функция свободного электронного газа
ne 2
( ) 1
0 m 2
23.
Диэлектрическая функция свободного электронного газаp2
( ) 1 2
Плазменная частота
ne 2
0 m
2
p
Зависимость диэлектрической функции от частоты
Электромагнитные волны
распространяются лишь при
( ) 0 . Когда ( ) 0
(отрицательна), то
электромагнитные волны
отражаются от среды.
Плазменной частоте р
соответствует длина волны
р 2 с / p
Электромагнитное излучение будет распространяться в среде только в
том случае, если в свободном пространстве длина волны этого
излучения будет меньше р .
24. Свободный электронный газ во внешних полях
Распространение электромагнитных волн в плазме(поперечные оптические моды)
Дисперсионный закон для электромагнитных волн ( ) с k
не дает волновых решений для отрицательной диэлектрической
проницаемости. Волны падающие на такую среду полностью
отражаются.
2
2
2
Электронный газ действует как частотный фильтр. Он становится
прозрачным лишь для волн с частотами p .
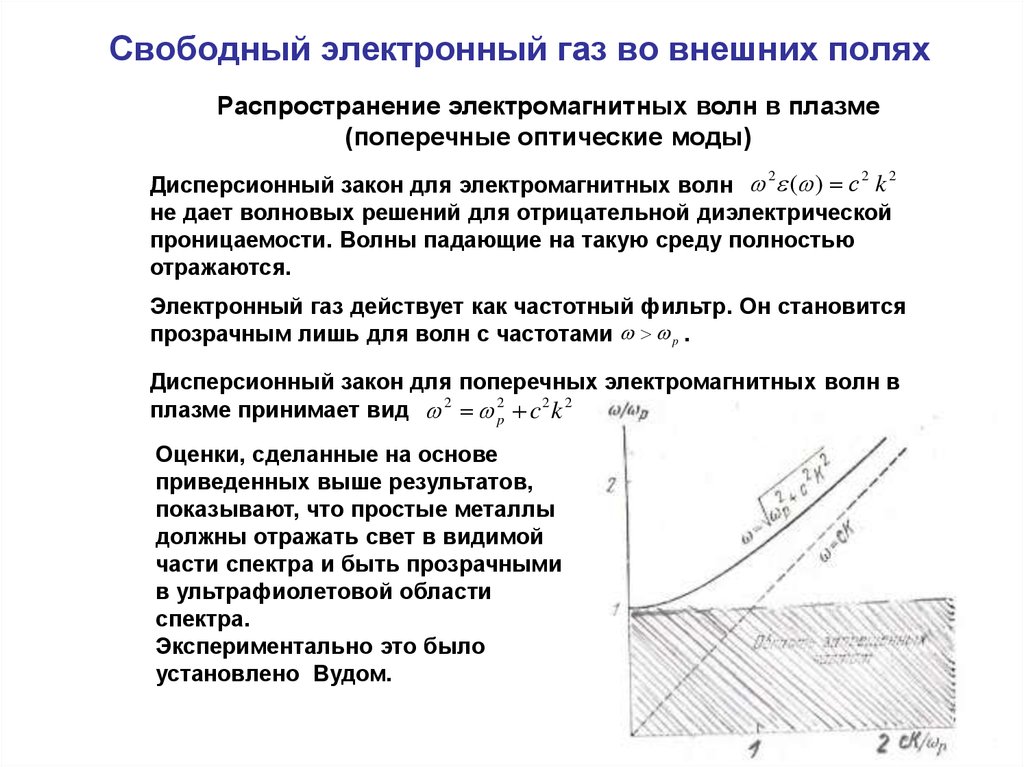
Дисперсионный закон для поперечных электромагнитных волн в
плазме принимает вид 2 p2 c 2 k 2
Оценки, сделанные на основе
приведенных выше результатов,
показывают, что простые металлы
должны отражать свет в видимой
части спектра и быть прозрачными
в ультрафиолетовой области
спектра.
Экспериментально это было
установлено Вудом.
25. Свободный электронный газ во внешних полях
Распространение электромагнитных волн в плазме(продольные оптические моды)
Нули диэлектрической функции ( L ) 0 определяют частоты
продольных оптических мод L .
Сместим в тонкой металлической пластине электронный газ как
целое на расстояние uотносительно положительного ионного фона.
В результате смещения возникнет поверхностный заряд, который
создает электрическое поле E neu / 0 .
Уравнение движения единицы объема электронного газа запишется в
виде
2
nm
d u
2 2
neE
n
e u / 0
2
dt
1/ 2
ne 2
d u
2
p u 0; p
2
dt
m 0
2
Плазменные колебания в металлах есть коллективные продольные
возбуждения газа электронов проводимости с частотой р. Квант
энергии плазменных колебаний называется плазмоном.
Энергия плазмонов 3 – 30 эВ. Время жизни плазмона
~ 10 16
с.
26. Свободный электронный газ во внешних полях
Электростатическое экранированиеПриближенное описание электростатического экранирования можно
осуществить с помощью уравнения Пуассона:
e
2 (r ) [n(r ) n0 ]
0
Составим другое
уравнение, связывающее электростатический
(r
) с концентрацией электронов, исходя из того, что
потенциал
электрохимический потенциал электронного газа при равновесии
должен сохранять постоянную величину независимо от положения.
( r ) 0, электрохимический потенциал
В той части образца, где
связан с однородной концентрацией (при Т 0) соотношением
2
(3 2 n0 ) 2 / 3
2m
0
F
В той области образца, где электростатический потенциал равен
для электрохимического потенциала имеем:
2
F (r ) e (r )
[3 2 n(r )]2 / 3 e (r )
2m
(r ),
27. Свободный электронный газ во внешних полях
Электростатическое экранированиеПостоянство электрохимического
потенциала приводит к выражению
2
2
[3 2 n(r )]2 / 3 e (r )
[3 2 n0 ]2 / 3
2m
2m
Качественный смысл приведенного
выражения иллюстрируется на рисунке:
показаны две точки, взятые в электронном газе, отличающиеся на
локальный потенциал (r ) . Распределение
Ферми в точке (2) сдвинуто
на величину потенциальной энергии e (r ) . Чтобы уровень сохранил
свое значение, необходимо, чтобы изменилась плотность электронов в
окрестности точки (2).
При разложении приведенного выражения в ряд Тейлора, получим:
d F
[n(r ) n0 ] e (r )
dn0
Подставляя
n(r ) n0
3
e (r )
n(r ) n0 n0
2
F
в уравнение Пуассона, получим:
3 n0 e 2
2
2 0 F
2
2
3
n
e
2 0
2 0 F
28. Свободный электронный газ во внешних полях
Электростатическое экранированиеМы ищем потенциал, обладающий сферической симметрией
d2 2 d
2
(r ) 2 (r )
r dr
dr
Потенциал, удовлетворяющий этому уравнению, имеет вид
qe r
(r )
r
и называется экранированным кулоновским потенциалом.
Длина экранирования
определяется как величина,
обратная постоянной . Например,
в меди концентрация электронов
равна n0 8,5 10 22 электрон / см,3 а
длина экранирования 1/ = 0,55 A .
29. Свободный электронный газ во внешних полях
Электрон-электронные столкновенияВ металле электроны проводимости находятся на расстоянии 1-3 A друг
4
относительно друга, проходят расстояния от 10 A (при комнатной
температуре) до 10 см (при 1 К) не сталкиваясь. Это обусловлено двумя
обстоятельствами. Первое – принцип Паули, второе – экранирование
кулоновского взаимодействия.
Оценим влияние принципа Паули в случае двухчастичного
столкновения 1+2 → 3+4.
Эта схема описывает
столкновение электрона в
возбужденном состоянии 1 с
электроном в состоянии 2
внутри сферы Ферми рис. а)
и невозможность
столкновения рис. б).
Закон сохранения энергии требует, чтобы , | 2 | 1 так как в противном
случае условие 3 4 1 2 не может быть выполнено.
Это означает, что столкновения возможны в том случае, если состояние 2
лежит внутри слоя толщиной 1 внутри поверхности Ферми.
30. Свободный электронный газ во внешних полях
Электрон-электронные столкновенияПодходящей мишенью для электрона 1 является не любой электрон, а
лишь электрон из заполненного слоя, в котором число электронов
составляет долю ~ 1 / F всего их числа.
Даже если электрон-мишень 2 находится в
нужном слое, лишь небольшая часть
конечных состояний совместима с законами
сохранения энергии и импульса и допустима
по принципу Паули. Это обстоятельство
уменьшает допустимое количество еще на
множитель 1 / F (рис. в).
Если 1 порядка k BT , то уменьшение частоты электрон-электронных
столкновений относительно классической величины будет характеризоваться
множителем (k BT / F ) 2 , а для эффективного сечения столкновений получим
2
выражение
k T
el el B 0
F
Численные расчеты показывают, что эффективное сечение столкновения
0 между электронами с учетом экранирования порядка 10 15 см 2 .
2
При комнатной температуре k BT / F 10 , а следовательно ~ 10 4 0 ~ 10 19 см 2 .
31.
Средняя длина свободного пробега при комнатной температуре дляэлектрон-электронных столкновений равна по порядку величины 10 4 см (
lel el 1 / n ). Эта величина на порядок больше, чем средняя длина свободного
пробега для электрон-фононного взаимодействия при комнатной
температуре. Это значит, что электроны сталкиваются преимущественно с
фононами.
Таким образом, принцип Паули дает ответ на один из центральных
вопросов теории металлов: почему электроны проходят в металле такие
большие расстояния, не сталкиваясь между собой.
32. Свободный электронный газ во внешних полях
Движение в магнитном полеk
Под действием силы F все точки сферы Ферми испытывают смещение в
- пространстве на k ; уравнение движения имеет вид:
dp
p
F
dt
или
1
d
F
k
dt
Слагаемое (d / dt ) k описывает ускорение свободной частицы, а
эффект столкновений (аналог трения) описывается членом k / .
В однородном магнитном поле на каждый электрон действует сила
Лорентца
1
Поскольку
F e ( E B )
с
m k
, то уравнение движения примет вид
d 1
1
m e E B
c
dt
Приращение скорости
по поверхности Ферми.
представляет собой среднее значение взятое
33. Движение в магнитном поле
Циклотронная частотаРассмотрим уравнение движения для случая, когда
поле B
направлено вдоль оси z. Для простоты положим E 0, а .
Уравнение движения в компонентах по осям х и y, примет вид
d
eB
d
eB
m y
x
m x y ;
dt
c
dt
c
Решения этой системы уравнений имеют вид
x 0 cos ct;
где частота
y 0 sin ct ,
с и есть циклотронная частота для свободного электрона
с
eB
mc
Амплитудное значение скорости 0 не является скоростью Ферми; это
просто какое-то значение начальной дрейфовой скорости электрона на
поверхности Ферми.
Для свободного электрона в поле 10 кГс получим: с 1,76 10 рад/сек.
9
Если время релаксации равно 2 10 14 сек при температуре 300 К и 2 10
3
2
сек при 4 К, то для Cu имеем соответственно c 3,5 10 и 3,5 10 .
11
Циклотронная орбита при комнатной температуре никогда не может
сформироваться, а при гелиевых температурах электрон до столкновения
проходит по орбите много витков.
34. Движение в магнитном поле
Статическое магнетосопротвлениеВ постоянном магнитном поле, направленном по оси z, уравнение
движения электронов имеет вид
B
B
d 1
d 1
m x e E x y ; m y e E y x ;
c
c
dt
dt
d 1
m z e E z .
dt
В стационарных условиях производная по времени равна нулю, и
уравнение движения получим в виде:
e
x E x c y ;
m
e
y E y c x ;
m
z
Решая эту систему уравнений относительно x и y, получим
x
e / m
( E x c E y ),
2
1 ( c )
e / m
y
( E y c E x ).
2
1 ( c )
e
Ez .
m
35. Движение в магнитном поле
Статическое магнетосопротвлениеПлотность тока для электронов описывается соотношением
J n( e) .
Для компонент вектора плотности электрического тока соответственно
имеем:
J x xx E x xy E y
J y yx E x yy E y
0
( E x c E y ),
2
1 ( c )
0
( c E x E y ),
2
1 ( c )
J z zz Ez .
2
Здесь 0 ne / m . Плотность тока можно записать в матричной форме
Jx
0
Jy
2
1 ( c )
Jz
1
E x
c
0
0
c 1
E y
2
E
0
0
1
(
)
c
z
Диагональные элементы тензора проводимости xx и yy ,
характеризующие эффект магнетосопротивления, при увеличении
величины магнитного поля монотонно убывают. Недиагональные
элементы xу и yx при увеличении величины магнитного поля
сначала возрастают, а затем убывают.
36. Движение в магнитном поле
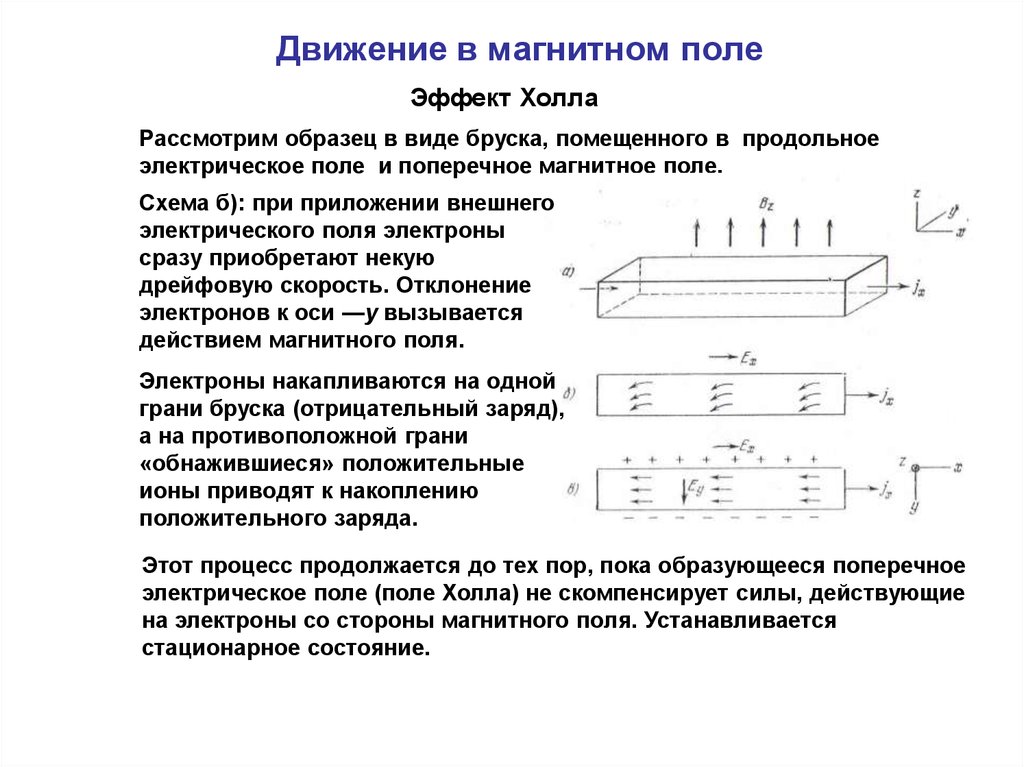
Эффект ХоллаРассмотрим образец в виде бруска, помещенного в продольное
электрическое поле и поперечное магнитное поле.
Схема б): при приложении внешнего
электрического поля электроны
сразу приобретают некую
дрейфовую скорость. Отклонение
электронов к оси —у вызывается
действием магнитного поля.
Электроны накапливаются на одной
грани бруска (отрицательный заряд),
а на противоположной грани
«обнажившиеся» положительные
ионы приводят к накоплению
положительного заряда.
Этот процесс продолжается до тех пор, пока образующееся поперечное
электрическое поле (поле Холла) не скомпенсирует силы, действующие
на электроны со стороны магнитного поля. Устанавливается
стационарное состояние.
37. Движение в магнитном поле
Эффект ХоллаЧтобы получить выражение для поля Холла воспользуемся
системой уравнений, полученных для компонент плотности тока.
В рассматриваемой геометрии опыта ток не может «вытекать» из
бруска в направлении оси y , то следует положить J y 0
E y c E x
eB
Ex
mc
Ey
Поле E y называют полем Холла, а величину RH
JxB
Холла.
RH
постоянной
eB E x / mc
1
ne 2 E x B / m
nec
Для свободных электронов постоянная Холла – величина
отрицательная. В некоторых металлах RH положителен и поэтому
носители должны иметь знак «+». Формула Холла позволяет
определить, действительно ли все валентные электроны
превращаются в электроны проводимости.
38. Недостатки модели свободных электронов
Коэффициент Холла константа не зависящая от температуры, временирелаксации и напряженности магнитного поля. Тем не менее он зависит
от температуры и напряженности магнитного поля. В алюминии в три
раза отличается от вычисленных значений RH , сильно зависит от
напряженности магнитного поля и имеет «+» знак. Лишь в щелочных
металлах наблюдается хорошее согласие с расчетом.
Закон Видемана-Франца выполняется в области высоких и низких
температур, а в промежуточной области величина / Т зависит от
температуры.
Температурная зависимость статической электропроводности не
находит объяснения в модели свободных электронов.
Высокочастотная электропроводность. Оптические свойства металлов
настолько сложно зависят от частоты, что их нельзя получить из простой
диэлектрической проницаемости, к которой приводит модель.
Бессмысленно пытаться объяснить цвет меди или золота, исходя из
коэффициентов отражения, рассчитанных по диэлектрической
проницаемости в модели свободных электронов.



































 Физика
Физика








