Механические колебания

1. Лекция № 5

МЕХАНИЧЕСКИЕ
КОЛЕБАНИЯ

2.

Колебания – это движения или
процессы, характеризуемые той или иной
степенью повторяемости во времени.
Колебательные процессы в природе:
колебания уровня воды в водоемах, биение
сердца и т.д.
В технике колебания могут играть как
положительную
роль
(маятник,
колебательный контур, пневмолоток и т.д.),
так и отрицательную (вибрации машин и
сооружений, неустойчивость при движении
тел и т.д.).

3.

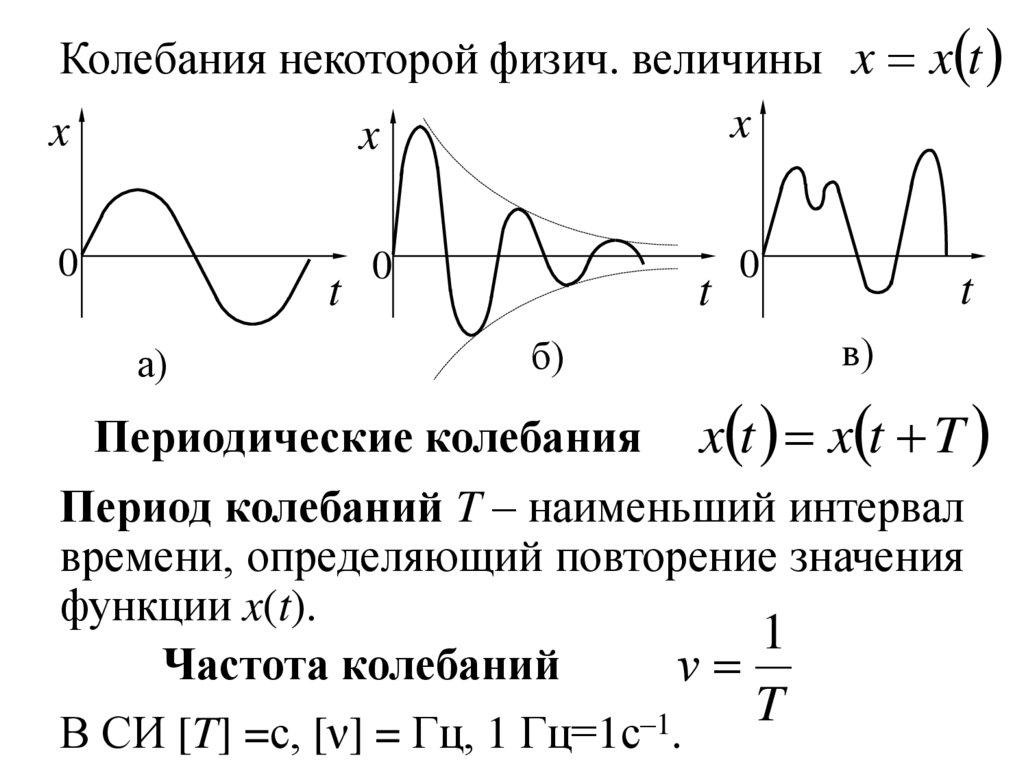
Колебания некоторой физич. величины x x t
x
x
x
0
t
а)
0
t
б)
Периодические колебания
0
t
в)
x t x t T
Период колебаний T – наименьший интервал
времени, определяющий повторение значения
функции x(t).
1
Частота колебаний
ν
T
–1
В СИ [T] =с, [ν] = Гц, 1 Гц=1с .

4. Гармонические колебания

– простейшие периодические колебания, при
которых изменение физической величины
происходит по закону синуса или косинуса.
x A cos 0t , x A sin 0t , (5.1)
где A – амплитуда колебаний, (ω0t + ) – фаза
колебаний, – начальная фаза.
ω0 – круговая или циклическая
частота гармонических колебаний:
2
0
2 ν
T
В СИ ω0=[с–1]

5.

x A cos 0t ,
dx
x A 0 sin 0t
dt
2
d x
2
x A 0 cos 0t
2
dt
Дифференциальное уравнение
гармонических колебаний:
(ДУ)
x 02 x 0
– однородное ДУ второго порядка, его общее
решение имеет вид (5.1).

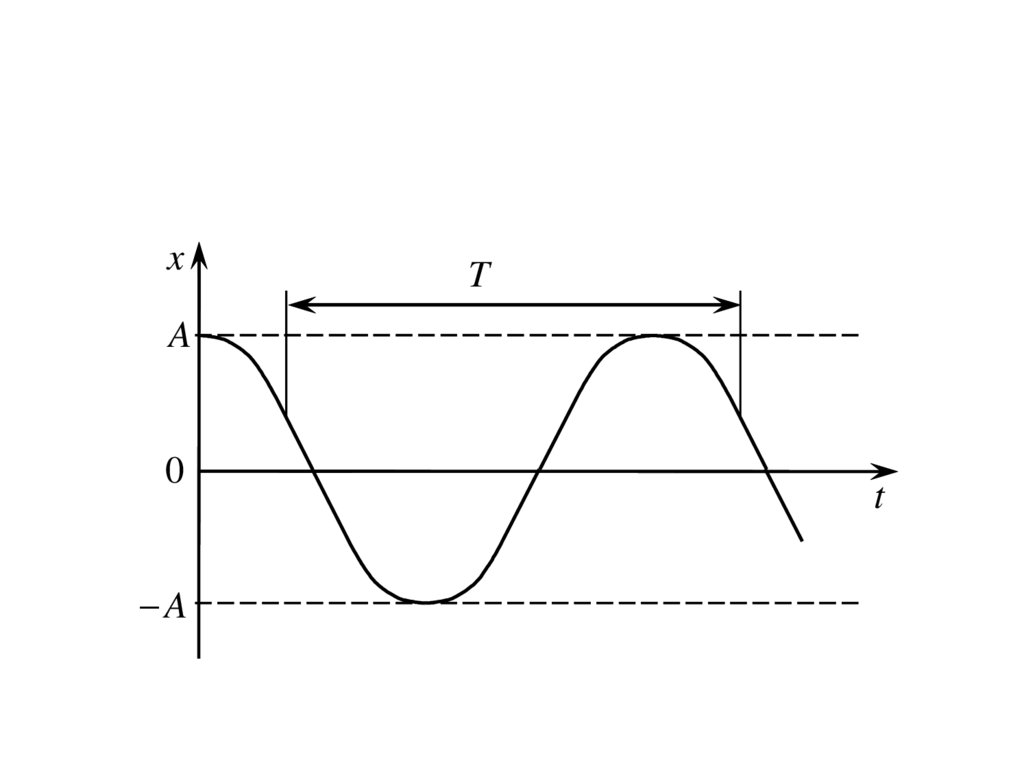
6.

x
T
A
0
A
t

7. Свободные незатухающие колебания (СНК) – (собственные гармонические колебания)

происходят в консервативных колебательных
системах.
Рассмотрим СНК пружинного маятника.
Масса пружины << массы груза m.
k – коэффициент упругости пружины.

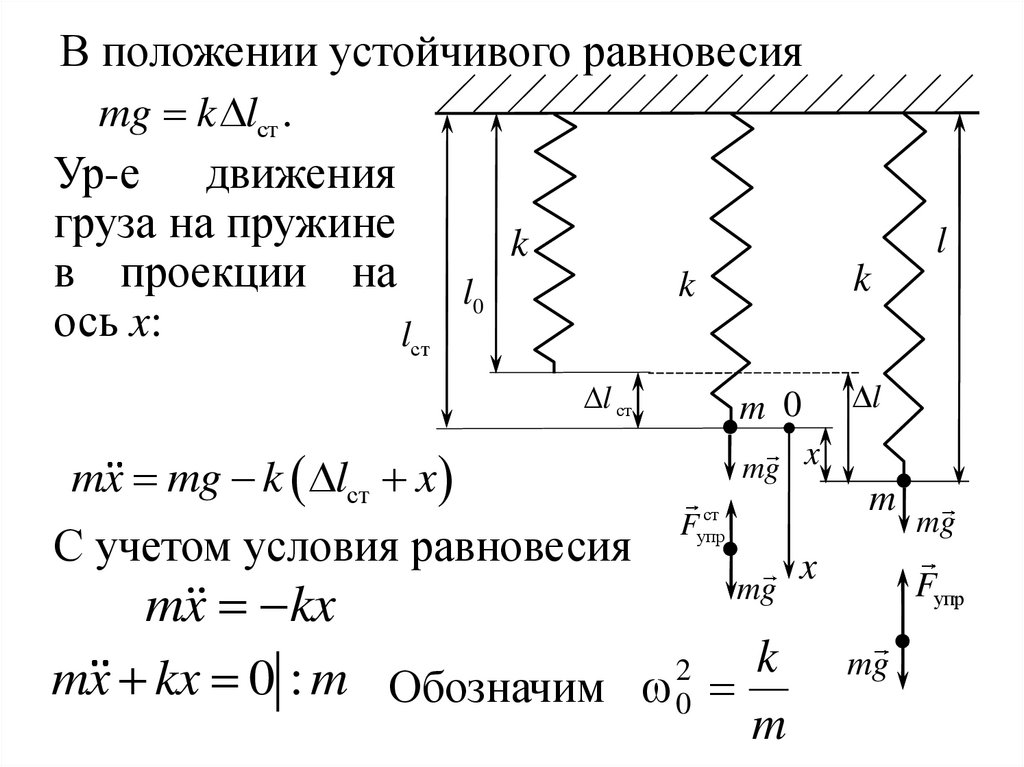
8.

В положении устойчивого равновесия
mg k lст .
Ур-е движения
груза на пружине
k
в проекции на l
0
ось x:
lст
l
k
k
l ст
mx mg k lст x
С учетом условия равновесия
m 0
mg x
ст
упр
F
m x kx
k
2
mx kx 0 : m Обозначим 0
mg
m
l
m
x
mg
Fупр
mg

9.

ДУ СНК пружинного маятника
2
x 0 x 0
Решение ДУ:
x A cos 0 t
Скорость груза
x A 0 sin 0t ,
его ускорение
2
a x A 0 cos 0t

10.

Начальные условия (НУ) при t = 0:
x 0 x0 ; 0 0
x0
cos ;
A
x0 A cos ;
Тогда
0
sin
.
A 0
0 A 0 sin .
Отсюда:
A
0
2
x0
0
2
0
; tg
x0 0

11. Энергия и импульс гармонического осциллятора

Осциллятор – система, совершающая
l0
колебания.
m
k
x1 0
x2 x x
l x
m
k
l
Fупр
m
Полная механическая энергия СНК
пружинного маятника в любой момент
2
2
времени:
m
kx
E Ek E p
2
2

12.

Кинетическая энергия системы
1
m
2 2
2
Ek
mA 0 sin 0t ,
2
2
потенциальная энергия
2
1
kx 2
2 2
2
mA 0 cos 0t
Ep
2
2
2
k m 0
Полная
осциллятора:
энергия
гармонического
1
E mA2 02 const
2
В консервативной сист. выполняется ЗСМЭ.

13.

Фазовая
траектория
зависимости p = p(x).
–
график
Импульс гармонического осциллятора:
p m mA 0 sin 0t
2
p
sin 0t 2 2 2
m A 0
2
Из (5.1)
2
x
cos 0 t 2
A
2

14.

С учетом
cos 0t sin 0t 1
2
2
приходим
к
уравнению,
которое
в
координатной плоскости x, p (фазовой
плоскости) является уравнением эллипса:
p
2
x
2
x
p
1
2
2 2 2
A
m A 0
Каждому эллипсу определенный
уровень энергии осциллятора E.

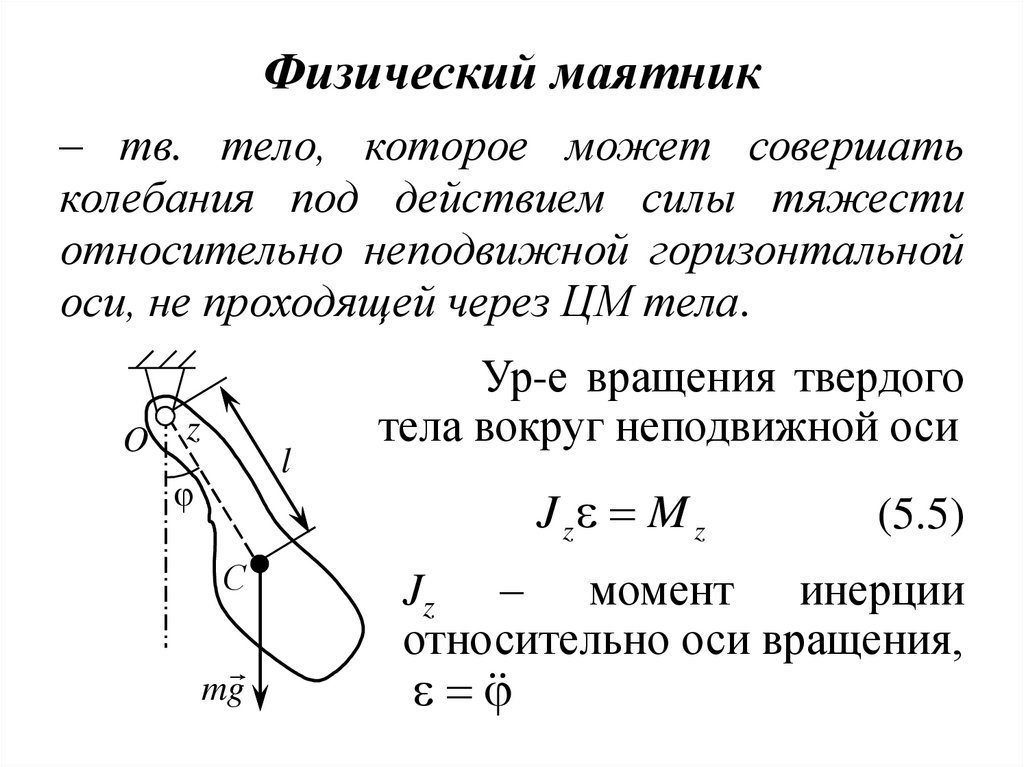
15. Физический маятник

– тв. тело, которое может совершать
колебания под действием силы тяжести
относительно неподвижной горизонтальной
оси, не проходящей через ЦМ тела.
O
z
l
С
mg
Ур-е вращения твердого
тела вокруг неподвижной оси
J z M z
(5.5)
Jz – момент инерции
относительно оси вращения,

16.

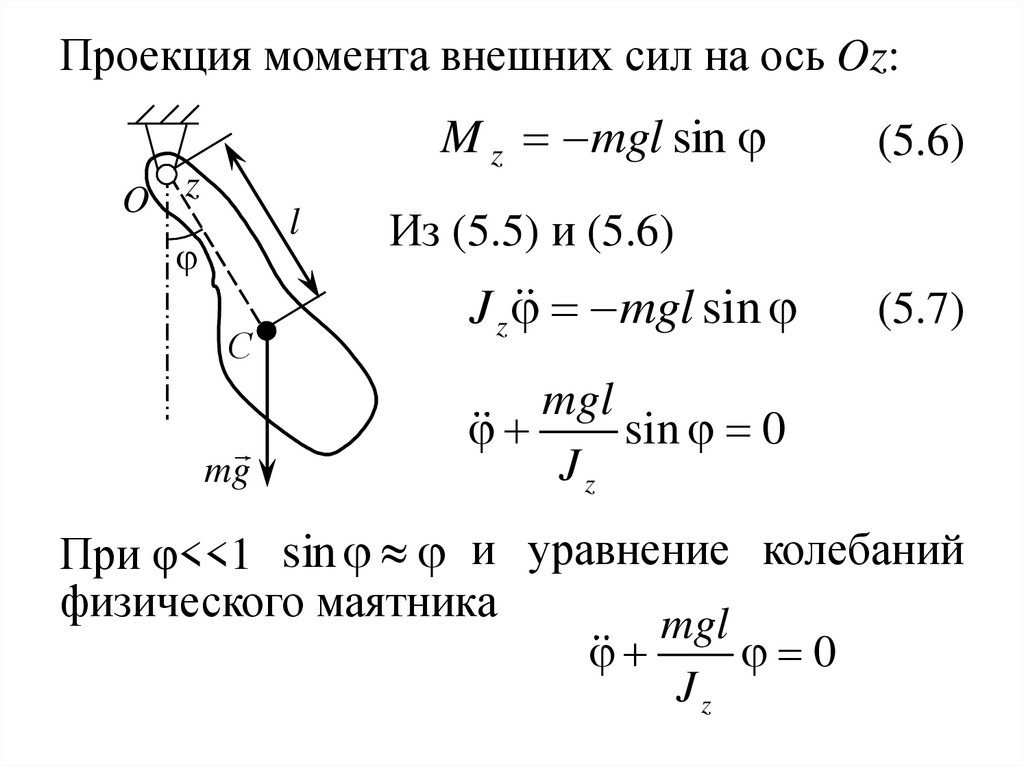
Проекция момента внешних сил на ось Oz:
M z mgl sin
O z
l
С
mg
(5.6)
Из (5.5) и (5.6)
J z mgl sin
(5.7)
mgl
sin 0
Jz
При φ<<1 sin и уравнение колебаний
физического маятника
mgl
0
Jz

17.

ДУ СНК
2
0 0,
mgl
Jz
(5.8)
2
0
его решение:
A cos 0t ,
2
0
T
Период малых колебаний физического
маятника
Jz
T 2
(5.9)
mgl

18.

Всякому физическому маятнику можно
сопоставить
математический
маятник
(точечное тело, подвешенное на невесомой
нерастяжимой нити), имеющий такую же
~
частоту колебаний. Длина нити l такого
математического
маятника
называется
приведенной длиной физического маятника.
g
0 M ~
l
ωM – частота колебаний математического
маятника. Отсюда
g
~
l
2
0

19. Квазиупругая сила

Квазиупругие силы – силы, физическая
природа которых отлична от упругих сил, но
определяющая их зависимость имеет вид:
Fx kx,
где k – постоянный коэффициент, x –
смещение физического объекта относительно
положения равновесия. Если на тело
действует квазиупругая сила, то оно
совершает
свободные
гармонические
колебания.