Похожие презентации:
Распределение напряжений в грунтовом массиве и принцип линейной деформируемости грунтов
1. РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В ГРУНТОВОМ МАССИВЕ и принцип линейной деформируемости грунтов
Министерство образования и науки Российской ФедерацииФГОУ ВО Новосибирский государственный архитектурностроительный университет (Сибстрин)
РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В
ГРУНТОВОМ МАССИВЕ
и принцип линейной
деформируемости грунтов
1
Новосибирск, 2016
2.
23.
34.
Но…нормативные документы рекомендуют
использовать для решения задач механики
грунтов законы теории упругости, которые
применяют к задачам о напряженнодеформированном состоянии (н.д.с.) сплошных
упругих изотропных тел.
Чтобы решения теории упругости можно было
использовать для грунтов, приходится принимать
ряд допущений и вносить некоторые
ограничения.
5.
56.
67.
Принцип линейной деформируемостизаключается в допущении линейной связи между
напряжениями и деформациями и формулируется
так: при небольших изменениях давлений можно
рассматривать грунты как линейнодеформируемые тела, т.е. с достаточной для
практических целей точностью можно принимать
зависимость между относительными
деформациями и напряжениями для грунтов
линейной. Это допущение позволяет использовать
ТУ внутри грунтового основания при условии :
р ˂ Р1
8.
89.
910.
Если разгрузить штамп после уплотнения грунтаоснования нагрузкой N, еще не вызвавшей
интенсивных местных сдвигов, то после полной
разгрузки кривая никогда не возвратится в начало
координат, т.к. грунт получает остаточные
деформации, следовательно, и грунт не является
упругим телом. Вследствие этого, решения ТУ для
изотропных тел можно использовать лишь при
однократном загружении основания.
Грунт обладает зернистостью и анизотропностью,
но принимается условно, что грунт является
сплошным телом.
Т.о. при определении напряжений в грунтом массиве
принимают допущения, что грунт является
сплошным линейно-деформируемым телом,
испытывающим однократное загружение.
11.
Задача БуссинескаЭто первая задача определения напряжения от действиясосредоточенной силы на линейно-деформируемое
полупространство. Полупространство – это часть
пространства, ограниченная плоскостью.
Модель, предложенная Буссинеском:
Линейно – деформируема (выполняется принцип
линейной деформируемости);
2. Однородна (в каждой точке свойства одинаковы);
3. Изотропна (в любом направлении свойства
одинаковы).
1.
12.
Определение напряжений в массиве грунтаПри определении напряжений в массиве грунта используют
законы механики для упругого сплошного тела.
Насколько грунты удовлетворяют данным требованиям?
Доказательство применимости теории упругости к
грунтам (постулаты теории упругости):
а) деформации пропорциональны напряжениям; грунт с
известными допущениями можно считать упругим телом;
в) Теория упругости рассматривает тела сплошные
г)Теория упругости рассматривает тела изотропные.
С известными допущениями грунт можно считать
изотропным телом
С учетом допущений можно применять теорию упругости
13.
1) Действие сосредоточенной силы (Задача Буссинеска)– является основной задачей в теории распределения
напряжений в грунтах (1885 г.).
N
О
Y
R
β
r
3 N z3
z 5
2 R
(4.1)
N
z K 2
z
(4.2)
z
M
Z
где K - табличный коэффициент,
зависящий от соотношения r/z.
13
14.
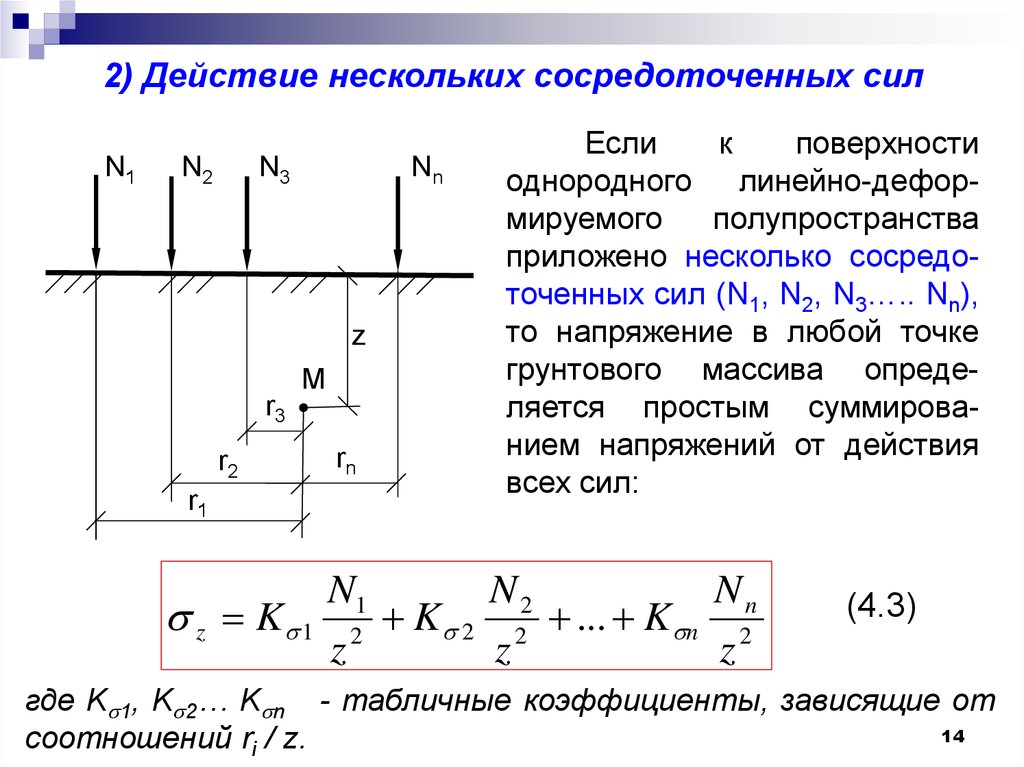
2) Действие нескольких сосредоточенных силN1
N2
N3
Nn
z
M
r3
r2
r1
z K 1
rn
Если
к
поверхности
однородного линейно-деформируемого
полупространства
приложено несколько сосредоточенных сил (N1, N2, N3….. Nn),
то напряжение в любой точке
грунтового массива определяется простым суммированием напряжений от действия
всех сил:
Nn
N1
N2
K 2 2 ... K n 2
2
z
z
z
(4.3)
где K 1, K 2… K n - табличные коэффициенты, зависящие от
14
соотношений ri / z.
15.
3) Действие любой распределенной нагрузкиДля определения сжимающих
напряжений z используют способ
Y
элементарного суммирования:
площадь
загрузки
делят
на
Ri
небольшие элементы и нагрузку
z
M
li
прикладывают в центре тяжести
каждого элемента как сосредоточенную.
bi
n
Ni
z K i 2
M
(4.4)
z
i 1
ri
где K I – коэффициент, определяемый
по таблице в зависимости от
отношения ri /z
При Ri > 2li погрешность определения напряжений будет
составлять около 6% (в сторону увеличения напряжений);
Ni
при Ri > 3li – 3%; при Ri > 4li – не более 2%.
15
16.
4) Действие равномерно распределенной нагрузкипо круглым и прямоугольным площадкам
Р
Впервые решение этой задачи в
1935 году получил профессор А. Ляв:
Y
z
M Z
b
C
O
X l
zc
Y
P l b z l 2 b 2 2z 2
l b
2 2
arcsin
2
2
2
2
D l b D 2 z 2
l z b z
(4.5)
2
D
где D – детерминант; l 2 b 2 z 2
2
Под центром прямоугольной
круглой площадки загружения:
zo 0 P
или
(4.6)
Под углом прямоугольной или краем круглой площади загружения:
zс 0,25 с P
(4.7)
z l
c f ;
b b
(4.9)
где z0 и zc – табличные коэффициенты (СНиП 2.02.01-83*):
2z l
0 f ;
b b
(4.8)
16
17.
4.5 Метод угловых точекСущность метода заключается в том, что грузовая
площадь разбивается на такие прямоугольники, в которых
рассматриваемая точка оказалась бы угловой.
Сжимающее напряжение z в этой точке будет равно
сумме напряжений от прямоугольных площадей загрузки,
для которых эта точка является угловой.
Рассмотрим три основных случая:
I Точка М находится на контуре загруженного
прямоугольника:
I
M
z zI zII 0,25( I II )P (4.10)
II
17
18.
II Точка М находится внутри прямоугольника:I
M
IV
0,25( ) P
II
z
III
zI
zII
I
zIII
II
III
zIV
(4.11)
IV
III Точка М находится за пределами прямоугольника:
z 0,25( I II III IV ) P
III
I
(4.12)
M
II
IV
z 0,25( I II III IV ) P
III
I
II
M
IV
(4.13)
18
19.
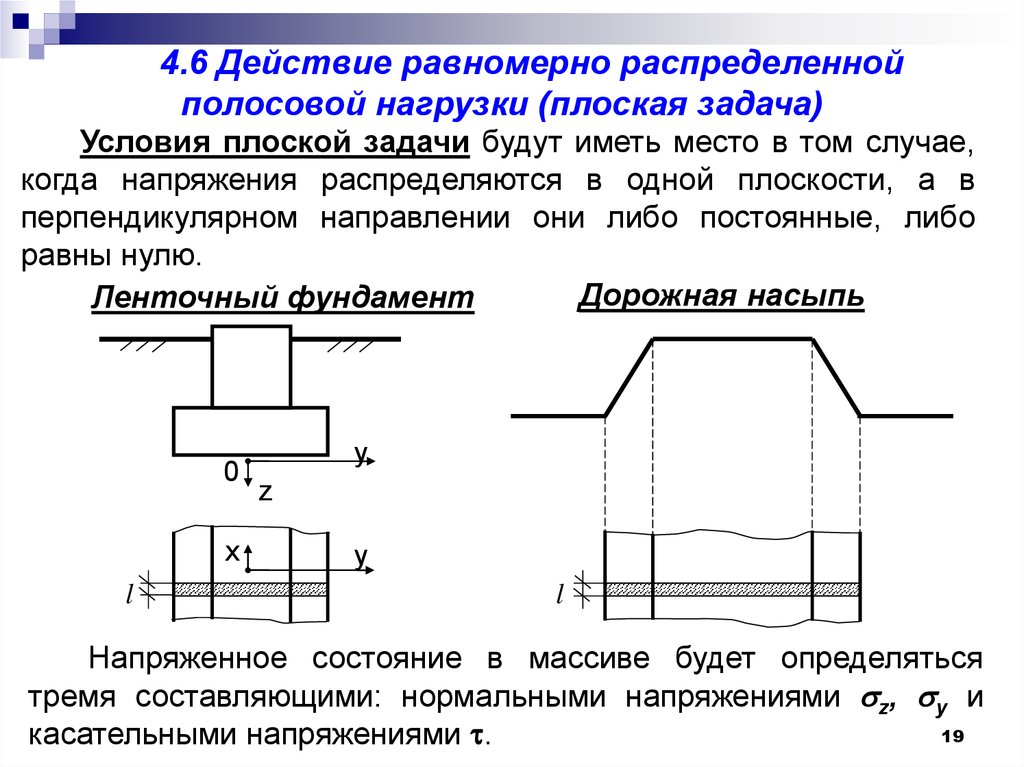
4.6 Действие равномерно распределеннойполосовой нагрузки (плоская задача)
Условия плоской задачи будут иметь место в том случае,
когда напряжения распределяются в одной плоскости, а в
перпендикулярном направлении они либо постоянные, либо
равны нулю.
Дорожная насыпь
Ленточный фундамент
0
x
l
y
z
y
l
Напряженное состояние в массиве будет определяться
тремя составляющими: нормальными напряжениями z, y и
19
касательными напряжениями .
20.
Выражения для этих напряжений получены на основерешения Фламана (1892 г.) для сосредоточенной силы в
условиях плоской деформации.
dy
b
Р
y
R
y
z
М
0
dP
β
z
- угол видимости;
R – расстояние от
начала координат до
рассматриваемой
точки;
β – угол между радиусом и осью z.
P
z sin cos 2
P
y sin cos 2
P
sin sin 2
(4.14)
z K z P
y K y P
K yz P
(4.15)
где Kz, Ky, Kyz – коэффициенты
влияния, определяемые по таблице в
зависимости от относительных
20
координат z/b и y/b.
21.
Напряженное состояние в грунтовом массиве в случаеплоской задачи может также определяться через главные
напряжения (Митчел, 1902).
Главные – это наибольшие и наименьшие
нормальные напряжения.
Главные напряжения будут возникать на площадках,
расположенных по вертикальной оси симметрии нагрузки
(при β=0), по биссектрисам углов видимости и площадках,
им перпендикулярным.
Главные напряжения можно вычислить из выражений
(4.14) подставляя в них угол β=0:
P
z sin
P
(4.16)
sin
y
0
21
22.
Эпюры распределения сжимающих напряжений zпо вертикальным (а) и горизонтальным (б)
сечениям массива грунта
22
23.
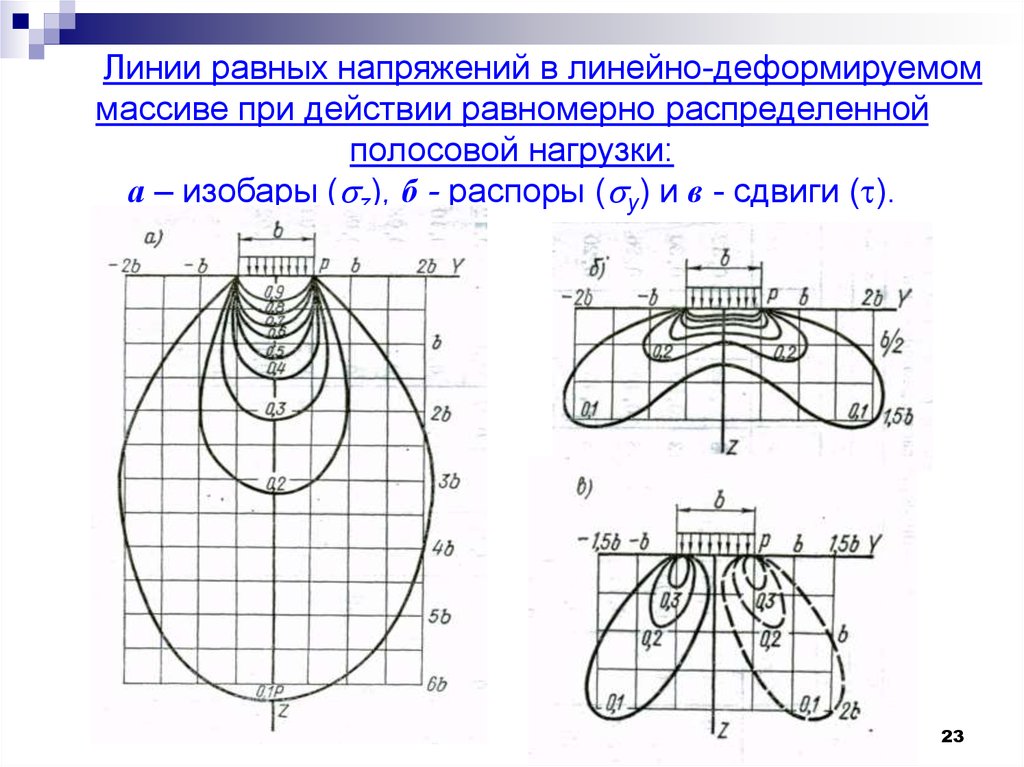
Линии равных напряжений в линейно-деформируемоммассиве при действии равномерно распределенной
полосовой нагрузки:
а – изобары ( z), б - распоры ( y) и в - сдвиги ( ).
23
24.
Эллипсы напряжений при действии равномернораспределенной нагрузки в условиях плоской задачи
24
25.
4.7 Распределение напряжений от действиясобственного веса грунта
Напряжения от собственного веса грунта увеличиваются
с глубиной.
1) При однородном грунтовом
постоянном удельном весе грунта):
0
Эпюра zq
основании
zq z
(при
(4.17)
где = g – удельный вес грунта;
z – глубина заложения
рассматриваемой точки.
z, м
25
26.
2) Для грунтовой массы (полностью водонасыщенногогрунта):
0
zq z
(4.18)
Эпюра zq
z, м
где ’ = ’ g – удельный вес грунта с
учетом взвешивающего действия воды
(плотность с учетом взвешивающего
действия воды определяется по формуле
(2.16) - s w ).
1 e
3) При неоднородной грунтовой толщи:
0
h1
0
zq
I слой
h2
2 > 1
h1
n
zq
II слой h2
z, м
z, м
УГВ
zq i hi (4.19)
i 1
где I – удельный вес i-го
слоя грунта;
hi – толщина i-го слоя.
26























 География
География








