Комплексные числа

1.

2.

Комплексным числом называется
выражение вида
z x i y
где х и у – действительные числа,
i – мнимая единица:
i 2 1

3.

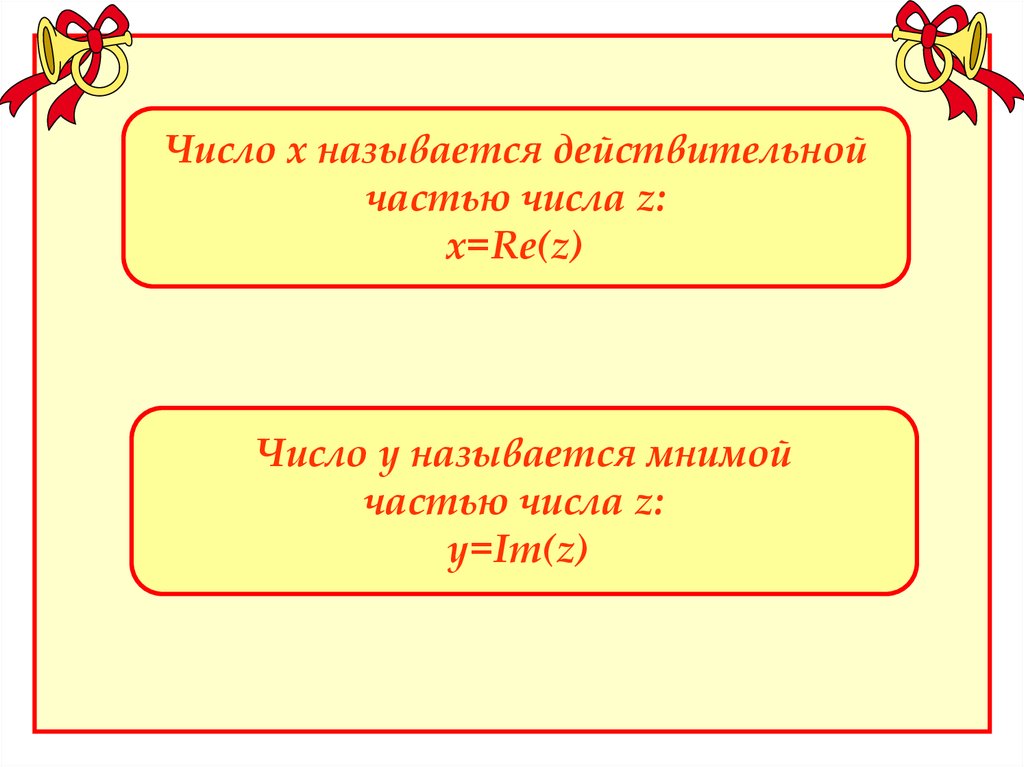
Число х называется действительной
частью числа z:
х=Re(z)
Число у называется мнимой
частью числа z:
у=Im(z)

4.

Действительное число х является
частным случаем комплексного числа
z x i y
при у=0.
Комплексные числа вида z x i y
не являющиеся действительными, т.е.
при
y 0
называются мнимыми, а при
x 0,
y 0
называются чисто мнимыми.

5.

Комплексные числа
z x i y
z x i y
называются сопряженными
Комплексные числа
z1 x1 i y1
z2 x2 i y2
называются равными, если равны их
действительные и мнимые части:
Re( z1 ) Re( z2 ) x1 x2
z1 z2
Im( z1 ) Im( z2 ) y1 y2

6.

1
Сумма (разность) комплексных чисел:
z1 z2 x1 x2 i ( y1 y2 )

7.

2
Произведение комплексных чисел:
z1 z2 ( x1 x2 y1 y2 ) i ( x1 y2 x2 y1 )

8.

Поскольку
z1 z2 ( x1 i y1 ) ( x2 i y2 )
x1 x2 x1 i y2 x2 i y1 y1 y2
( x1 x2 y1 y2 ) i ( x1 y2 x2 y1 )
Например:
i 2 i i (0 i 1) (0 i 1)
(0 1) i (0 0) 1

9.

3
Деление комплексных чисел:
z1 ( x1 x2 y1 y2 ) i ( x2 y1 x1 y2 )
2
2
z2
x2 y 2

10.

Поскольку
z1 x1 i y1 x1 i y1 x2 i y2
z 2 x2 i y 2 x2 i y 2 x2 i y 2
( x1 x2 y1 y2 ) i ( x2 y1 x1 y2 )
2
2
x2 y 2

11.

Найти сумму, разность, произведение
и частное комплексных чисел:
z1 12 5 i
z2 3 4 i

12.

z1 z2 12 5 i 3 4 i 15 i
z1 z2 12 5 i (3 4 i) 9 9 i
z1 z2 (12 5 i) (3 4 i) 36 15 i 48 i 20
56 33 i
z1 12 5 i 12 5 i 3 4 i
z2 3 4 i
3 4 i 3 4 i
36 15 i 48 i 20 16 63 i
0.64 2.52 i
9 16
25

13.

Если для изображения действительных
чисел используются точки числовой
прямой,
то
для
изображения
комплексных чисел используются точки
координатной плоскости ХОУ.
Плоскость называется комплексной, если
любому комплексному числу
z x i y
ставятся в соответствие точки плоскости
ХОУ, причем это соответствие взаимно
однозначное.

14.

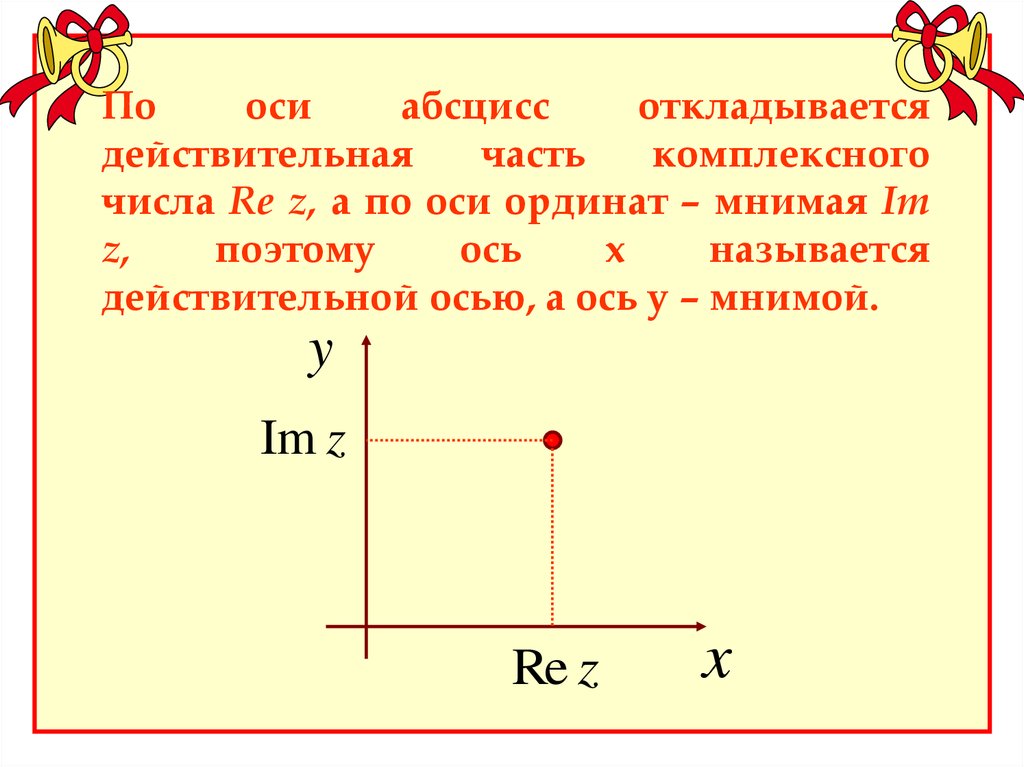
По
оси
абсцисс
откладывается
действительная
часть
комплексного
числа Re z, а по оси ординат – мнимая Im
z,
поэтому
ось
х
называется
действительной осью, а ось у – мнимой.
y
Im z
Re z
x