Теорема Гаусса-Остроградского

1.

Эта формула связывает интеграл по
объему V с интегралом по
поверхности S, ограничивающей этот
объем.

2.

Пусть V – некоторая область в
пространстве, S – граница этой области.
Если функции P(x,y,z), Q(x,y,z), R(x,y,z)
непрерывны вместе со своими
частными производными во всех точках
области V, то справедлива формула:

3.

P Q R
dV
x y z
V
P cos Q cos R cos dS
S
Где α, β, γ – углы, образованные внешней
нормалью и осями x,y,z.

4.

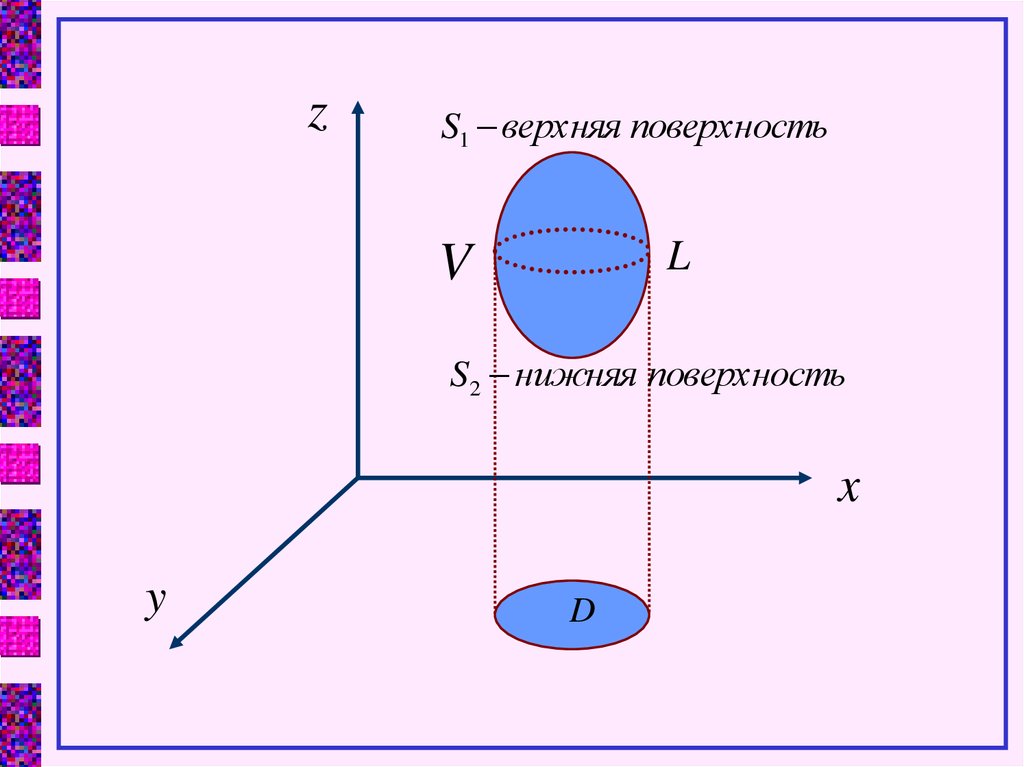
Рассмотрим
область
V,
поверхностью S.
Пусть существует интеграл
ограниченную
P Q R
dV
x y z
V
Проведем
цилиндрическую
поверхность,
проектирующую область V на плоскость ХОУ.

5.

z
S1 верхняя поверхность
L
V
S2 нижняя поверхность
x
y
D

6.

D – проекция областей S1 и S2 на плоскость ХОУ.
S1 : z1=z1(x,y)
S2 : z2=z2(x,y)
Сначала проинтегрируем по z:
R
R
dxdydz dxdy
dz
z
z
V
D
z1 ( x , y )
z2 ( x , y )
R( x, y, z2 ( x, y )) dxdy R( x, y, z1 ( x, y )) dxdy
D
D
Учтем, что
R( x, y, z) cos dG R( x, y, z( x, y))dxdy
S
D

7.

R( x, y, z ) cos dG R( x, y, z ) cos dG
S2
S1
R( x, y, z ) cos dG R( x, y, z ) cos dG
S2
S1
Верхняя и нижняя стороны являются внешними
сторонами поверхности S, поэтому
R
dxdydz R cos dG
z
V
S
1

8.

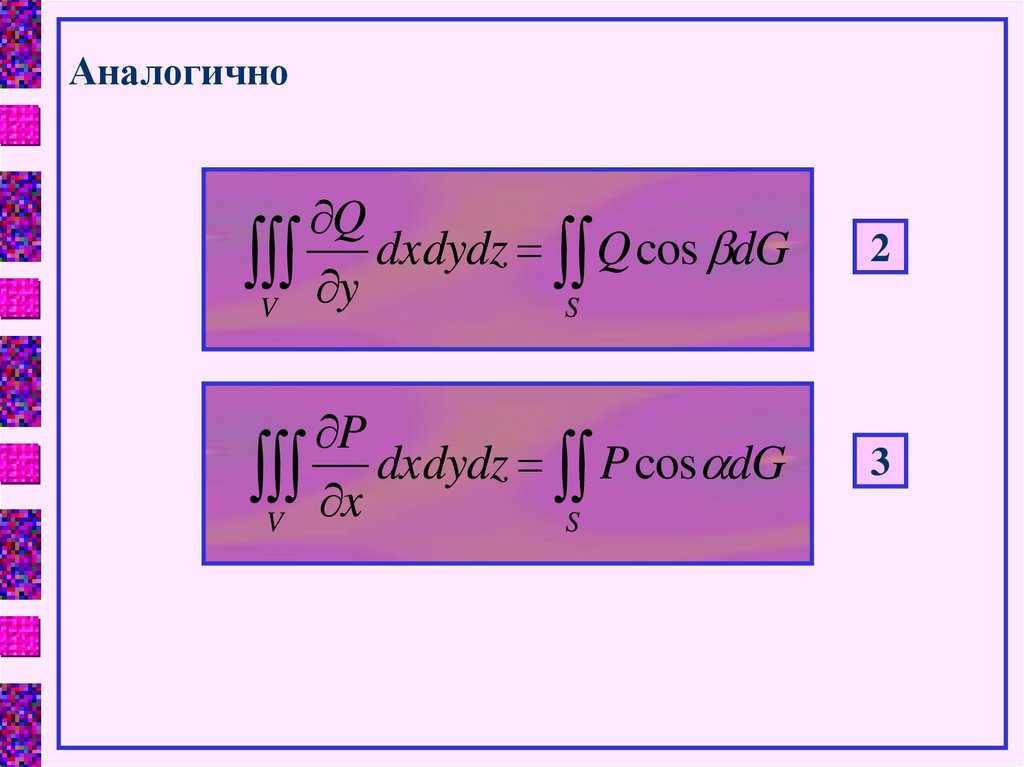
Аналогично
Q
dxdydz Q cos dG
y
V
S
2
P
dxdydz P cos dG
x
V
S
3

9.

Складываем почленно (1), (2), (3):
P Q R
dV
x y z
V
P cos Q cos R cos dS
S