Похожие презентации:
Интеграл от функции комплексного переменного; теорема Коши для составного контура, интегральная теорема Коши. Лекция 33
1. Лекция 33. Интеграл от функции комплексного переменного; теорема Коши для составного контура, интегральная теорема Коши.
Степенные ряды в комплексной области. РядТейлора, ряд Лорана, классификация особых
точек.
1
2.
§ 1. Интегрирование функции комплексногопеременного.
Пусть на комплексной плоскости задана кривая
AB – ориентированная, незамкнутая, кусочногладкая, без самопересечений.
Задание кривой z(t) эквивалентно следующему:
z (t ) x(t ) iy (t )
t
3.
4.
и – действительные числа.x(t), y(t) – действительные числа.
Разобьем AB произвольным образом:
A z0 , z1 , z2 zn B
Найдем разности двух составляющих
комплексного числа.
z0 z1 z0 , z1 z2 z1, , zn 1 zn zn 1
На каждом из участков выберем произвольные
точки 0 , 1 , , n 1
5.
Они отвечает соответствующим комплекснымчислам.
Пусть на комплексной плоскости, в том числе и на
дуге AB определена комплексная функция f(z).
Найдем ее значения в точках: f ( 0 ), f ( 1 ), , f ( n 1 )
n 1
и составим сумму вида:
интегральная сумма.
f ( k ) zk
k 0
- это
6.
Определение. (интеграла)Если существует предел интегральной суммы
n 1
lim f (
max | z k | 0 k 0
k
) zk
при max | zk | 0, k 0,1, , n 1
не зависящий от способа разбиения дуги AB и
выбора точек k , то этот предел называют
интегралом по дуге AB и обозначают:
f ( z )dz
AB
n 1
lim
max | z k | 0
f (
k 0
k
) z k
7.
Теорема. (о существовании интеграла отфункции комплексного переменного)
Пусть функция f(x) непрерывна на некоторой
кривой L, которая является ориентируемой,
кусочно-гладкой, незамкнутой, тогда интеграл по
дуге L от этой функции существует.
Доказательство.
Рассмотрим интегральную сумму
n 1
f (
k 0
k
) zk , где k L и z k L
8.
Так как любую функцию комплексногопеременного можно представить в виде:
f ( k ) u ( xk , yk ) iv ( xk , yk )
Комплексное число можно представить в виде
zk xk i yk
Перемножим эти выражения
f ( k ) zk u ( xk , yk ) xk v( xk , yk ) yk
i u ( xk , yk ) yk v( xk , yk ) xk
(1)
9.
Значит в использованном выражении (1),интегральная сумма может быть записана в
виде:
n 1
n 1
n 1
k 0
k 0
k 0
f ( k ) zk (u xk v yk ) i (u yk v xk ) (2)
Перейдем к пределу в выражении (2),
получим:
lim
max zk 0
f ( k ) zk
max zk max ( xk ) ( yk ) 0
2
2
n 1
n 1
lim
(u xk v yk ) i (u yk v xk )
( xk , yk ) ( 0, 0 ) k 0
k 0
(3)
9
10.
Так как f(z) непрерывна на L, то непрерывныв любой точке u и v (т.к задание f(z)
равносильно заданию u и v)
В правой части (3) – интегральные суммы для
криволинейных интегралов 2 рода
Из непрерывности u и v следует, что
существуют криволинейные интегралы 2 рода
как предел своих интегральных сумм.
10
11.
Так как каждый из пределов входящий,входящий в правую часть (3) существует и
равен соответствующему криволинейному
интегралу, то существует и предел левой части
(3) и можем записать
L
f ( z )dz udx vdy i udy vdx
L
(4)
L
(4) может использоваться и для вычисления
интегралов от ФКП.
11
12.
Свойства интегралов от ФКП.1) Если L+ и L- две дуги, различающиеся только
ориентацией, то:
f ( z )dz f ( z )dz
L
2)
L
Af ( z) B ( z) dz A f ( z)dz B ( z)dz
L
3)
4)
L
f ( z )dz
L1 L2
L
f ( z )dz f ( z )dz
L1
L2
f ( z )dz M l
L
М – действительное число
l – длина дуги L
12
13.
§ 2. Понятие первообразной. ФормулаНьютона-Лейбница. Интегрирование по
частям и заменой переменной.
Пусть функция f(z) задана в некоторой
односвязной области D на комплексной
плоскости.
Если существует функция F(z) в области D,
такая что F (z) = f(z), то F(z) называется
первообразной для функции f(z).
13
14.
Теорема. (о первообразной)Если функция f(z) дифференцируема в
замкнутой, односвязной области D, то для нее
существует первообразная F(z), определенная
на D, которая задается формулой:
F ( z)
z
f ( )d
z0
Замечание 1: В отличии от функции
действительного
переменного
функцию
комплексного
переменного
необходимо
дифференцировать в замкнутой односвязной
области для существования первообразной.
14
15.
Замечание2:
Если
f(z)
непрерывна
в
односвязной области D, и интеграл по любому
замкнутому контуру, лежащему в этой области
=0, то в этом случае первообразная так же
существует.
Замечание
3:
Две
первообразные
ФКП
отличаются на константу.
15
16.
Теорема. (Ньютона- Лейбница)Если f(z) дифференцируема в односвязной
области D и z1, z0 произвольные точки D, а F(z)
какая либо первообразная для f(z), то
z1
f ( z )dz F ( z1 ) F ( z0 )
z0
Теорема. (интегрирование по частям)
Если f(z) и (z) дифференцируемы в
односвязной области D, z1, z0 – точки,
принадлежащие D, то
z1
f ( z) ( z)dz
z0
z1
f ( z ) ( z ) z ( z ) f ( z )dz
z1
0
z0
16
17.
Для ФКП, при дифференцировании в областиD, можно использовать таблицу интегралов:
z1
n 1 z1
z
z dz n 1
z0
z
n
и т.д.
0
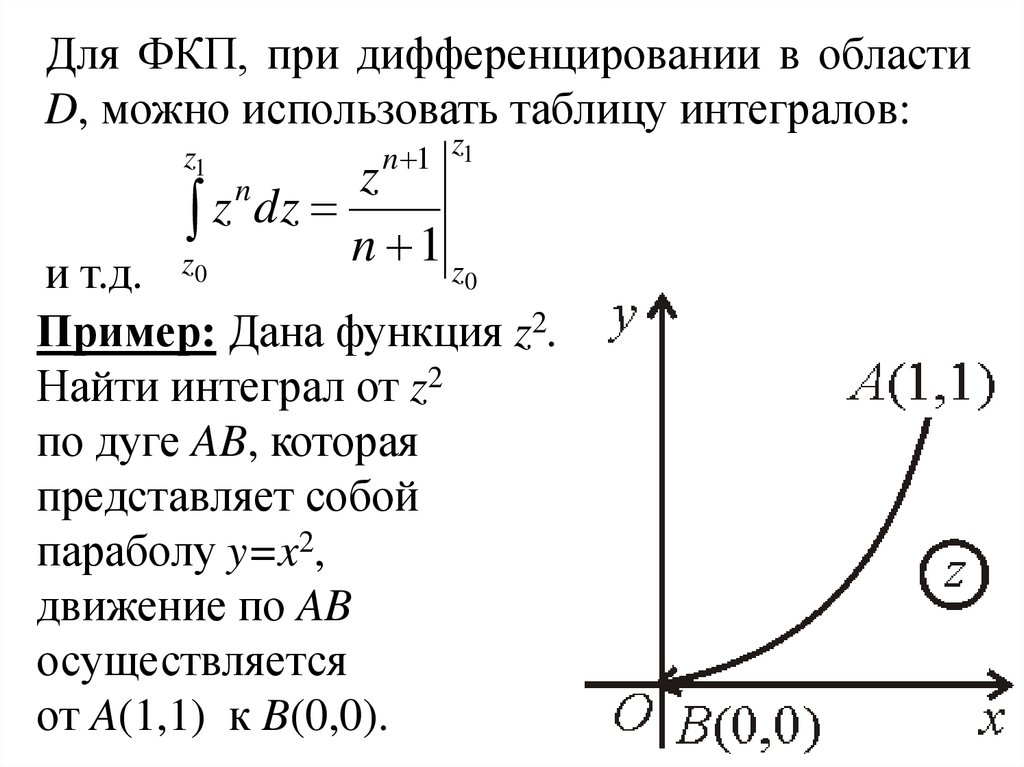
Пример: Дана функция z2.
Найти интеграл от z2
по дуге AB, которая
представляет собой
параболу y=x2,
движение по AB
осуществляется
от A(1,1) к B(0,0).
17
18.
z2
udx vdy i udy vdx *
dz
AB
z2
AB
AB
= (x + iy)2 = x2 – y2 + i2xy
u
v
тогда:
2
2
2
2
* ( x y )dx 2 xydy i ( x y )dy 2 xydx
AB
AB
x t dx dt, t [1;0]
2
y t dy 2tdt, ò.ê. A B
0
0
(t t ) dt 2t t 2t dt i (t t ) 2tdt
2
4
1
2
2
4
1
2t t dt 13 13 54 i ( 24 13 24 ) 23 i 23
2
19.
2-й способ решения с помощью формулыНьютона-Лейбница:
z1
3 z1
z
2
z dz 3
z0
z0
3
z0 1 i
(1 i )3
1
i 4
2e
3
3
z1 0
2 2 i 34
2 2
e
(cos 34 i sin 34 ) 2 3 2 (
3
3
23 i 23
1
2
i
1
)
2
19
20.
§ 3. Интегральная теорема Коши.Если функция f(z) аналитична в односвязной
замкнутой области D, то интеграл от этой
функции по любому замкнутому контуру,
лежащему в этой области = 0, то есть:
f ( z )dz 0
L
L - произвольный контур.
Доказательство.
Так как f(z) аналитична в области D, значит
она дифференцируема в односвязной области D;
из дифференцируемости следует существование
интеграла в области D по любой кривой.
20
21.
Из аналитичности следует выполнениеусловий Коши-Римана
u v u
v
;
x y y
x
Пусть L - произвольный, ориентированный
замкнутый контур, в области D, тогда
(1)
f ( z )dz udx vdy i udy vdx
L
L
L
Q P
формула Грина
Pdx
Qdy
(
)
dxdy
D* x y
Из аналитичности f(z) следует
дифференцируемость в области. Применим к
криволинейному интегралу 2-го рода, стоящему
в правой части (1) формулу Грина:
21
22.
L0
0
v u
u v
f ( z )dz dxdy i dxdy 0
y
y
D* x
D* x
D* - область, лежащая внутри L
Из условий Коши-Римана имеем, что
подынтегральное выражение = 0.
Значит интеграл от аналитической односвязной
функции = 0 по любому замкнутому контуру.
Если область D не является односвязной
теорему в этой формулировке применить нельзя
22
23.
Теорема. Если функция f (z) аналитична внеодносвязанной замкнутой области D с
конечным числом вырезов, то f (z) dz по
границе области D, обходимый в
положительном направлении = 0.
Без доказательства.
Следствие теоремы Коши для
неодносвязанной области. Если f (z)
аналитична в неодносвязанной области D с
границей L, то справедлива следующая
n
формула: f ( z )dz
f ( z )dz
L
i 1 Li
23
24.
Li – граница вырезов, обход которойпроизводится в том же направлении, что и обход
границы L.
§ 4. Некоторые основные формулы
интегрального исчисления.
dz
n
2
i
(
z
z
)
z z
0 dz 0
0
L
L
Теорема. (интегральная формула Коши).
Если функция f (z) аналитична в замкнутой
односвязанной области D с положительно
ориентированной, кусочно-гладкой границей L,
то значение функции в любой точке zk D
1 f ( z )dz
находится по формуле: f ( zk )
2 i L z zk
24
25.
Примечание. Значения функции в областиопределяются своими значениями на границе.
Без доказательства.
Интеграл Коши
Пусть функция f (z) аналитична в некоторой
области D лежащей на комплексной плоскости.
Пусть в области D имеется ориентированный
замкнутый контур L. Точка L.
Интегралом типа Коши в области D называется
интеграл вида:
1 f ( )d
2 i
L
z
Точки z лежат либо внутри, либо вне контура L.
25
26.
Свойства интеграла Коши1. Если z лежит вне контура L, z D, то
1 f ( )d
0
2 i L z
для z D, z L.
2. Если z лежит внутри контура L, z D, то
1 f ( )d
f ( z)
2 i L z
Значение функции аналитической в области
определяется значением на границе.
26
27.
Если кривая L незамкнута, то говорят обинтеграле типа Коши
1 f ( )d
2 i z
где - незамкнутая ориентируемая кривая,
лежащая в области D.
Интеграл типа Коши обозначают:
1 f ( )d
F ( z)
2 i z
27
28.
Замечание. Если функция f (z)дифференцируема в области D, кривая L
замкнутая граница области D, то интеграл Коши
1 f ( )d
2 i L z
является бесконечно дифференцируемой в
области функцией, причем:
f
( n)
n!
f ( )d
( z)
n 1
2 i L ( z )
28
29.
Пример. Найти:z
e
( z 2i)5 dz 0
z 1
30.
Степенные ряды на комплексной плоскостиПусть z – произвольная точка комплексной плоскости
- фиксированная точка комплексной плоскости
Определение (Степенные ряды)
Степенным рядом к. плоскости называется ряд вида: an
(1)
a 0
Если
, то
an
(2)
n 0
Свойства степенных рядов (1) и (2) одинаковы.
Разница между ними только в областях сходимости.
Определение (Радиус сходимости степенного ряда)
Действительное число R > 0 называется радиусом сходимости ряда (2),
если для z R ряд сходится, а для z R ряд расходится.
Определение (круга сходимости). Множество чисел, где R – радиус
сходимости ряда (2) называется кругом сходимости ряда (2)
31.
Можно доказать:1) Радиусы сходимости рядов (1) и (2) одинаковы
2) Степенные ряды (1) и (2) можно на кругах сходимости
дифференцировать, интегрировать, над ними можно совершать операции
предельного перехода, при этом радиусы сходимости рядов не изменятся.
Для степенных рядом в комплексной области справедливы все свойства
и теоремы, доказанные ранее для степенных рядов.
Рядом Тейлора функции f (z ) аналитической в области D называется
ряд
, если:
n 0
1) Он сходится на области D
2) Сумма ряда сходится к f (z ) .
Если степенной ряд
a
сходится на круге z z 0 R ,то он
n
n 0
равномерно сходится на круге z z 0 R , где , R - действительные
числа > 0.
Теорема (Абеля) Если степенной ряд
an
сходится в т.
,то он
n 0
сходится для z z 0 . Если же
an
n 0
для z z 0 .
расходится в т.
, то он расходится
32.
Теорема (о соотношении степенных рядов и рядов Тейлора). Всякийстепенной ряд на своем круге сходимости является рядом Тейлора для своей
суммы
Доказательство:
Рассмотрим ряд
a
n
= f (z )
n 0
f (z ) - сумма ряда
Пусть ряд сходится на z z 0 R (круг)
+…
f ( z ) a0 a1( z z 0) a 2
Так как на круге сходимости степенной ряда является непрерывной
функцией, то подставляя вместо
, имеем:
f ( z 0) a0 a1 0 a 2 0 ...
На своем круге сходимости степенные ряды можно сколько угодно раз
дифференцировать, с учетом этого:
f ( z ) a1 2a2 ( z z0 ) 3a3 ( z z0 ) 2
Причем, полученный ряд сходится на своем круге сходимости.
f ( z 0) a1 0
f ( z ) 2 1 a 2 3 2a 3 z z 0 ...
При z z 0 f ( z 0) 2!а 2
33.
Можно получитьТ.о. выражая a0, a1..., получим
f ( z 0)
a0
0!
f ( z 0)
a1
1!
f ( z 0)
a2
2!
f n ( z 0)
an
n!
То есть, коэффициенты степенного ряда есть коэффициенты ряда
Тейлора, для функции f (z ) , которая является суммой ряда.
Это означает, что любой степенной ряд на круге сходимости является
рядом Тейлора для своей суммы.
Это разложение единственно, так как коэффициент определяется
единственным образом.
Теорема (об аналитичности степенных рядов). Всякий степенной ряд
a ( z z )n
n
0
на своем круге сходимости z z 0 R является аналитической
n 0
функцией. Причем, для коэффициента этого ряда справедлива формула:
1
f ( )
an
d
2 z z 0 R ( z 0) n 1
34.
Доказательство:Пусть ряд
a ( z z )n
n
0
сходится на круге z z 0 R к f (z )
n 0
Тогда для z z 0 R сходимость равномерная. На своем круге
сходимости степенные ряды можно дифференцировать:
f ( z ) an n( z z 0) n 1
n 1
Эта формула справедлива для z z z 0 R . Радиусы сходимости при
дифференцировании не меняются.
Значит f (z ) аналитична на круге z z 0 R
Так как ранее показали, что f (z ) аналитическая на круге z z 0 R ,
значит она бесконечно дифференцируема на этом круге, причем все
производные могут быть получены по формуле:
n!
f ( )
(*)
f n ( z)
d
2 z z 0 R ( z 0) n 1
Так как степенной ряд является рядом Тейлора для своей суммы, то
коэффициент
f n ( z 0)
=
an
n!
Применяя формулу (*), имеем:
1 n!
f ( )
d
n! 2 z z 0 R ( z 0) n 1
35.
ПРЕДСТАВЛЕНИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИСТЕПЕННЫМИ РЯДАМИ
Теорема. Если функция f (z ) аналитическая на круге z z 0 R , то она
представима на этом круге в виде f (z ) = an( z z 0) n , где ряд стоящий в
n 0
правой части является сходящимся к f (z ) на этом круге.
Доказательство:
Возьмем внутри круга R произвольную окружность L.
L – произвольная ориентированная окружность z z 0 R
Пусть z - произвольная точка круга, лежащая внутри L.
– произвольная точка окружности L
36.
Так как f (z ) аналитическая на круге, то она может быть представлена1
f ( )
в виде: f ( z )
d
2 L z
z z0
1
z0
1
Рассмотрим выражение
- эта функция неаналитическая будет
z
только на окружности L, внутри окружности L она будет аналитическая.
Представим функцию в виде:
1
1
1
z z 0 ( z z 0) ( z 0)(1 z z 0 )
z0
Для ФКП так же как и для ФДП можно применить стандартное
разложение в степенные ряды:
1
xn , x 1
1 x n 0
1
zn , z 1
Для ФКП
1 z n 0
Модуль z z 0 z 0
37.
Применяя к функции, которая получена в преобразованиях разложения,получаем:
1
1
1
z z0 n
(
)
z
z
0
z ( z 0)(1
) z 0 n 0 z 0
z0
z z0
Которая сходится, когда
1
z0
Сходящиеся ряды можно умножать на любые функции. С учетом этого:
1
( z z 0) n
z n 0 ( z 0)n 1
При этом сходимость не изменится. Ряд, стоящий в правой части
z z0
сходится в области
1, внутри области сходимость равномерная.
z0
Равномерно сходящиеся ряды можно умножать на любые функции, почленно
дифференцировать и интегрировать.
Умножим последнее выражение на f ( )
f ( )
f ( )
n
(
z
z
0)
z n 0 ( z 0) n 1
38.
Проинтегрируем полученное выражение, учитывая, что в правой частиравномерно сходящийся ряд. Интегрирование ведем по контуру L:
f ( )
f ( )
n
d
d
(
z
z
0)
z
( z 0)n 1
n
0
L
L
f n ( z 0)
( z z 0) n
2 f ( z ) 2
n!
n 0
z z0 R
Можно представить рядом
f n ( z 0)
f ( z)
( z z 0) n = (который является рядом Тейлора) =
n!
n 0
= an ( z z 0) n
n 0
Любую аналитическую функцию на круге можно представить в виде
степенной функции, которая является рядом Тейлора своей функции.
Рассматривать можно 2-мя способами:
1) Непосредственно по теореме
2) Используя табличные разложения
f n ( z 0)
f ( z)
( z z 0) n
n!
n 0
39.
Пример:Разложить функцию e z в ряд в окрестности точки z 0 i
разложению по степеням z i
(e z ) n
ez
e z
z 0 i
z0 i
n!
n!
n!
i
e
e z ( z i)n
n 0 n!
Полученный ряд равномерно сходится на всей комплексной плоскости
2) способ
n
z
z
e , z0 0
n 0 n!
( z i)n
z
z i i
i
e e
e
n!
n 0
40.
РЯДЫ ЛОРАНАЕсли функция аналитическая в круге, то в круге аналитическую
функцию можно разложить в ряд Тейлора:
r z z0 R
Если область аналитичности – кольцо, то в этом случае функцию
нельзя разложить в ряд Тейлора, но можно в ряд Лорана.
Если функция аналитическая в кольце r z z 0 R , то рядом Лорана
для функции f (z ) называется ряд вида:
n
a ( z z ) n , который:
n
0
n
1) Сходится в кольце r z z 0 R
2) Сходится в функции f ( z )
a ( z z )n
n
n
0
41.
f ( z)Замечание: Ряд Лорана
a ( z z )n
n
0
иногда представляют
n
следующим образом:
n
1
a n
n
n
n 0
n
n 0
n 1 ( z z 0 )
Выражение, обведенное скобкой называется правильной частью ряда
Лорана, а обведенное волнистой линией – главной частью ряда Лорана.
Теорема (разложение в ряды Лорана) Если функция f (z ) аналитична
и однозначна в кольце r z z 0 R , то она в этом кольце разлагается в ряд
Лорана.
n
1
f ( )
d
f ( z ) an( z z 0) n , где an
n 1
2 L ( z 0)
n
L – произвольный контур, лежащий в кольце.
an( z z 0)
n
an( z z 0)
n
an( z z 0)
n
Замечание. Правильная часть ряда Лорана
an( z z 0)
n
n
a
n
(
z
z
0
)
сходится для
n 0
z z0 R
a n
Главная часть ряда Лорана
сходится для z z 0 r (вне
n
n 1 ( z z 0 )
круга).
42.
Разложение в ряды Лорана осуществляются 2-мя способами:1) По теореме
2) С использованием табличных разложений
1
Пример: Функцию f ( z ) разложить в ряд Лорана в кольце 0 z 1
z
1-ый способ – по теореме:
1
Центром кольца является точка z 0 . Функция в кольце аналитична,
z
как частное аналитических функций, значит она раскладывается в ряд Лорана
1
1
1 d
1
an
d
( n 2) d
n 1
n 1
2 L ( 0)
2 L
2
dz
2
z z 0
1, n 1
L
n
0
,
n
1
( z z 0) dz 0, åñëè n 1
L
В соответствии с теоремой функция разлагается в ряд:
1,êîãäà n -1
1 n
anz , где an
z n
0
,êîãäà
n
1
Разложение состоит из одного члена:
1 1
z z
43.
2-ой способ – используя табличное разложение1
– Найти разложение этой функции.
f ( z)
( z 1)( z 2)
1. Для z 1
2. В кольце 1 z 2
3. z 2
1) Найдем при каких z функция не будет аналитической.
z 1, z 2
Так как z ei
ei 1; ei 2
Проведем окружности z 1; z 2
44.
Для того чтобы разложить функцию в круге z 1 , представимфункцию в виде:
1
1
1
1
1
1 1
1
f ( z)
( z 1)( z 2) z 2 z 1
2 z 1 z
21 z 1 z
2
Используя разложение в ряд типа геометрической прогрессии, имеем:
n
1
z z
, 1 z 2
z n
2
0 2
1
2
1
zn, z 1
1 z n 0
Сложим два разложения и получим:
n
1 z
f ( z ) z n из 2-х областей сходимости выбираем
2 n 0 2 n 0 z 1
z 2
1 n 1 n
наименьшую = 1 z , z 1 – ряд сходится.
2
n 0
45.
Разложение в ряд Лорана совпадает с разложением в ряд Тейлора, таккак функция аналитическая в круге. Правая часть ряда Лорана – ряд Тейлора.
Получим разложение для 2-го случаев:
1
1
1 1
1 1
f ( z)
z
1
z 2 z 1
21
z 1
z 2
z 1
2
z
n
n
1 z 1 1
zn
1
n 1 n 1
2 n 0 2
z n 0 z
n 0 2
n 0 z
z 2
z 1
Разложение для 3-го случая z 2 f (z ) – аналитическая.
1
1
1 1
1 1
1 2 n 1 1 n
f ( z)
(
) ( )
2
1
z 2 z 1 z 1
z 1
z n 0 z
z n 0 z
z 2
z 2
z 1
z
z
z 2
Оба ряда сходятся в наибольшей области z 2
n
2 1
z n 1
n 0
В данном случае имеет только главную часть ряда Лорана.
f ( z)
46.
Существенно особая точкаТочка z0 – особая точка функции f ( z ) называется существенно особой
точкой функции f ( z ) , если в разложении функции в ряд Лорана в главной
части содержится бесконечно большое число слагаемых, т.е.
a k
k
.
f ( z ) ak ( z z 0 )
k
k 0
k 1 ( z z 0 )
При этом lim f ( z ) не существует. Пользуются разложением в ряд
z z0
Лорана.
Пример:
f ( z ) исследовать на характер особой точки.
1
ez
f(z)
z 0 - нарушается аналитичность
n
1
1
1
z
еz
, z 0
n
n 0 n!
n 0 n! z
Т.к. в разложении в ряд Лорана присутствует бесконечное число
членов ряда, то точка z 0 0 - существенно особая точка.
47.
Предел ФКП не зависит от способа стремления, если зависит, тоговорят что он не .
lim
1
еx
lim
1
еx
e 0
x 0 0
x 0 0
Предел в данном случае зависит от способа стремления.
Замечание 1. Для того, чтобы точка z0 была изолированной особой
точкой функции f ( z ) необходимо и достаточно, чтобы она была нулем
1
функции
.
f(z)
Замечание 2. Для того, чтобы точка z 0 была полюсом f ( z )
1
необходимо и достаточно, чтобы она была нулем функции
.
f(z)
Теорема (необходимое и достаточное условие полюса m-того порядка)
Для того, чтобы т. z 0 - была полюсом m-того порядка f ( z ) , необходимо
( z )
чтобы f ( z ) была представлена в виде f ( z )
, ( z ) - аналитична в
m
( z z0 )
точке z 0 , ( z ) 0
48.
ДоказательствоДостаточность.
Пусть
f ( z ) представлена в виде
( z )
f(z)
, где ( z ) m
( z z0 )
аналитична в точке z 0 , ( z 0 ) 0 .
В силу аналитичности
( z ) a0 a1 ( z z 0 ) a2 ( z z 0 )2 ... ...am ( z z 0 )m am 1 ( z z 0 )m 1 ...
Тогда f ( z ) представляем в виде
f(z)
a0 a1 ( z z 0 ) ... ...a m ( z z 0 )m a m 1 ( z z 0 )m 1 ...
( z z 0 )m
Ряд сходящийся, следовательно, его можно делить на функцию
a0
a1
... a m a m 1 ( z z 0 ) ...
f(z)
m 1
m
( z z0 )
( z z0 )
в котором содержится только m членов главной части.
Точка z 0 - полюс функции m-того порядка.
Необходимость. Самостоятельно















































 Математика
Математика








