Свойства степеней с натуральным показателем

1.

Свойства степеней с
натуральным показателем.

2.

Повторяем.
Назовите основание и показатель степени
7
3
5;
42
b ;
2
;
5
6
1,3 ;
à ;
7
a ò ;
2
15 ;
6
3õ ; a õ ;
5
10
2
d .
9
3

3.

Выполните возведение в степень:
4
3
5;
2
1,1 ;
2
1
1 ;
3
2
0,3 ;
2
;
5
1 ;
8
2
5
;
6
2 ;
2 ;
4
5
4
2
;
3
2
3
8

4.

Представьте числа в виде квадрата или куба
числа:
9;
1000;
1
2 ;
4
0,36;
64;
216;
1
;
25
0,008;
1
;
8
36
;
144
8
.
125

5.

Вычислите:
3 4 ; 10 3 ;
5
2
3
3
( 3) 1 ;
3
5
19
7
1,25 4,25 ;
2
17 9 ; 1,5 8 ;
4
6
3 6 ;
5
6 ;
4
5 3 ;
3
4
17,7 2 3 .
6

6.

Умножение степеней
с одинаковыми основаниями
5 5 5 5 5 5 5 5
2
4
2 множ.
4 множ.
5 5 5 5 5 5 5
2 4 множителя
6

7.

Умножение степеней
Для любого числа а и произвольных натуральных
чисел m и n верно равенство
a a a
m
n
m n
Правило:
При умножении степеней с одинаковыми
основаниями основание оставляют прежним, а
показатели степеней складывают.

8.

Представьте произведение в виде степени:
5
3
y y ;
17 17 ; 1,8 1,8;
2 5
4
bb;
0
( 3) ( 3) ; k ( k ) ;
3
2
7
t tt t;
9
7
2 8;
3
4
6
5
4
m mm ;
1
0,125.
8

9.

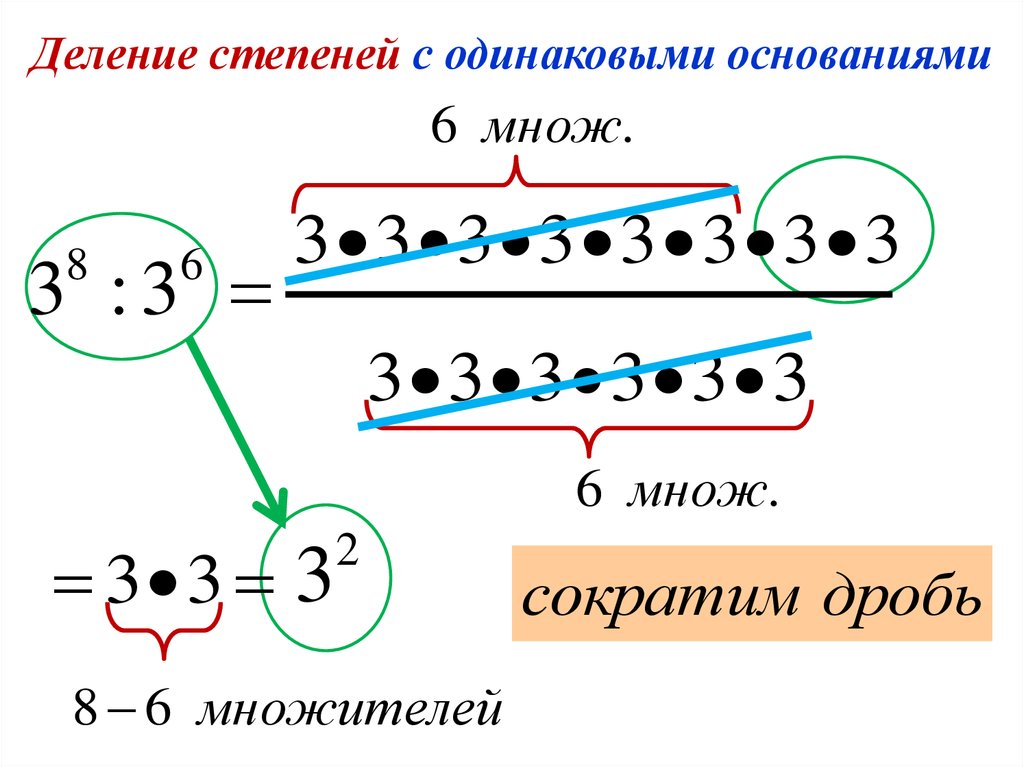
Деление степеней с одинаковыми основаниями
6 множ.
3 :3
8
6
3 3 3 3 3 3 3 3
3 3 3 3 3 3
6 множ.
3 3 3
2
8 6 множителей
сократим дробь

10.

Деление степеней
Для любого числа а ≠ 0 и произвольных натуральных
чисел m и n , таких что m > n верно равенство
a :a a
m
n
m n
Правило:
При делении степеней с одинаковыми основаниями
основание оставляют прежним, а из показателя
степени делимого вычитают показатель степени
делителя.

11.

Деление степеней
Степень числа а ≠ 0 с нулевым показателем
равна единице.
a 1
0
0
Например:
4
0
4 1; 1; ( 1,74) 1.
7
0
Выражение 00 не имеет смысла.

12.

Представьте частное в виде степени:
х : х ; b :b ;
6
12
4
10
а :а ;
4
k
3
6
1,8 : 1,8;
7
( 3) : ( 3) ;
7
2
t t : t t ;
2
3
7
( k )
4
;
5
4
2
14
2 : 8;
m : mm ;
4 2
: .
9 3

13.

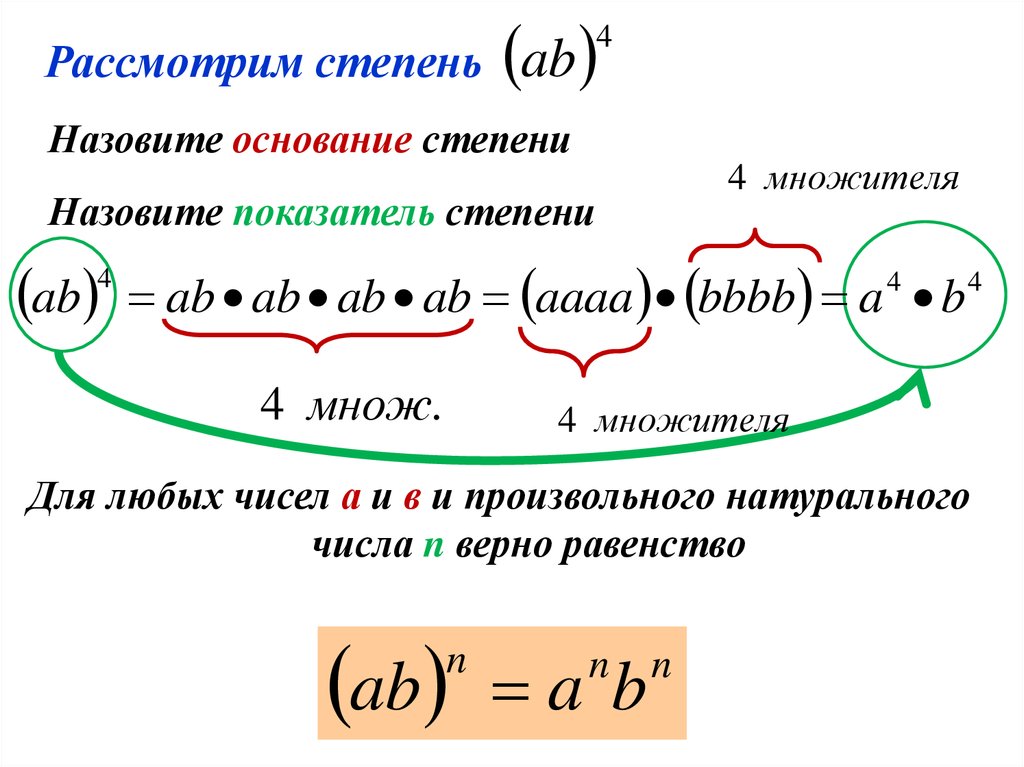
Рассмотрим степень
ab
4
Назовите основание степени
4 множителя
Назовите показатель степени
ab
4
4
4
ab ab ab ab aaaa bbbb a b
4 множ.
4 множителя
Для любых чисел а и в и произвольного натурального
числа n верно равенство
ab
n
a b
n
n

14.

ab
n
a b
n
n
Правило:
Чтобы возвести в степень произведение достаточно
возвести в эту степень каждый множитель и
результаты перемножить.
Свойство справедливо для степени из произведения
трех и более множителей
Свойство справедливо для степеней с нулевым
показателем (если основания отличны от нуля)

15.

Замените на произведение степень:
ху ;
abc
4
10
5
1
d ;
2
( 3 p) ;
2
0,5m ;
5
;
10а ;
3
kz ;
7
3
2
xaz .
3

16.

Рассмотрим степень
a
m n
Назовите основание степени
Назовите показатель степени
a
m n
n раз
a a ... a a
m
m
m
m m ... m
n раз
a
m n
Для любого числа а и произвольных натуральных
чисел n и m верно равенство
a
m n
a
m n

17.

a
m n
a
m n
Правило:
При возведении степени в степень основание
оставляют тем же, а показатели перемножают.
Свойство справедливо для степеней с нулевым
показателем (если основания отличны от нуля)
120
0 13
120 1
0

18.

Выполняя задание по преобразованию
выражений, содержащих степени, ученик
допустил ошибки:
1) 3 3 3 3 3 5 ;
3
2) 2 2 2 4;
2
3) 8 16;
2
4) 0 1;
0
Какие свойства степени не знает ученик?

19.

Выполняя задание по преобразованию
выражений, содержащих степени, ученик
допустил ошибки:
5) (3 4) 12 24;
2
6) 2
7) 8 1;
1
2
32;
2 3
8) 0 1;
0
Какие свойства степени не знает ученик?

20.

Выполняя задание по преобразованию
выражений, содержащих степени, ученик
допустил ошибки:
9) 3 3 3 ;
3 7
10) 5 5 25 ;
21
3 7
11) 2 2 2 ; 12) 3
3
7
10
300
10
100
:3
3 ;
3
Какие свойства степени не знает ученик?

21.

Выполняя задание по преобразованию
выражений, содержащих степени, ученик
допустил ошибки:
13) 3 3 3 ;
5 8
14) 5 5 10 ;
40
2 3
15) 2 2 2 ;
4
2
6
5
16) 3 : 3 3 ;
10
2
5
Какие свойства степени не знает ученик?

22.

Выполняя задание по преобразованию
выражений, содержащих степени, ученик
допустил ошибки:
17) 2a 2a ;
5
5
x ;
19) a a a a
18) x
3
2 3
2 4
8
2 7
14
;
Какие свойства степени не знает ученик?

23.

При каком значении k верно равенство?
20) 2 2 2 ;
2
k
6
21) 5 : 5 5 ;
6
k
2
22) 9 3 9 ;
2 k
23) 5
2 k
3
625;

24.

Вычислите
17
15
1 1
24) : ;
5 5
25) 2 : 2 ;
21
18
Сравните выражения. Ответ обоснуйте
26) 2b 2b ;
2
2

25.

Сравните с нулем значение выражения
27) 11 11 0; 28) 6 6 0;
9
8
4
10
29) 14 : 14 0; 30) 3 : 3 0;
25
31) х : х 0;
6
20
13
8
33) с
2 25
5
32) а 0;
2
0; 34) р
0.
10 2

26. Рефлексия