Решение задач

1.

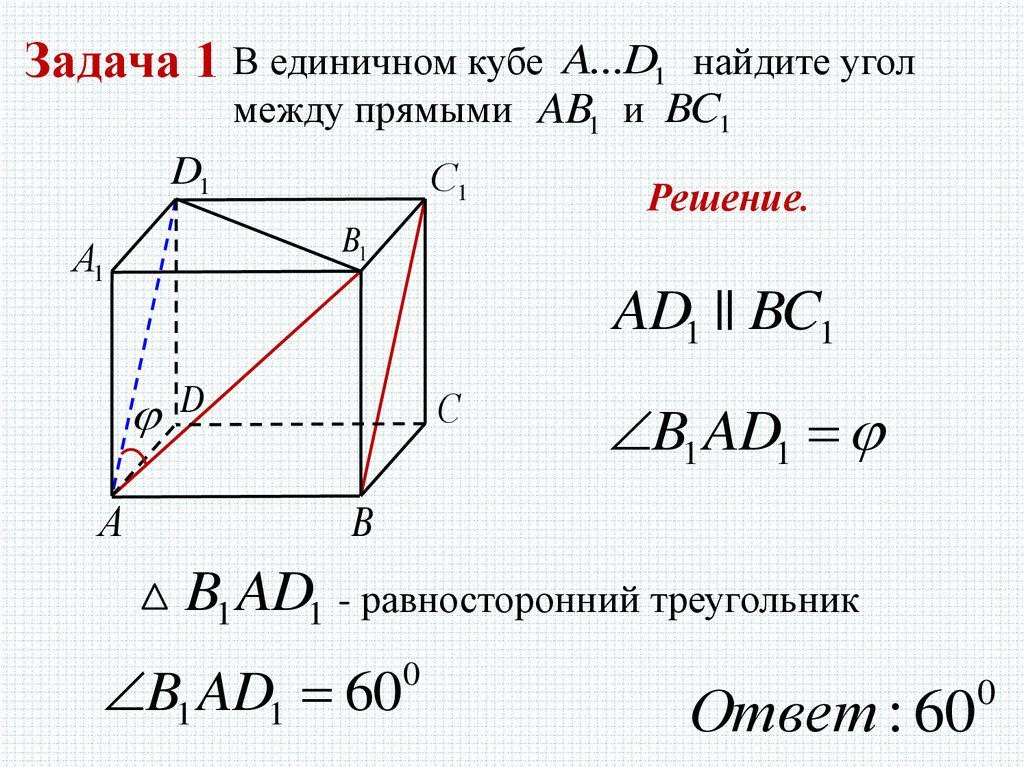
Задача 1 В единичном кубе A...D1
найдите угол
между прямыми AB1 и BC1
С1
D1
Решение.
B1
А1
AD1 || BC1
D
А
С
B1 AD1
B
B1 AD1 - равносторонний треугольник
B1 AD1 60
0
Ответ : 60
0

2.

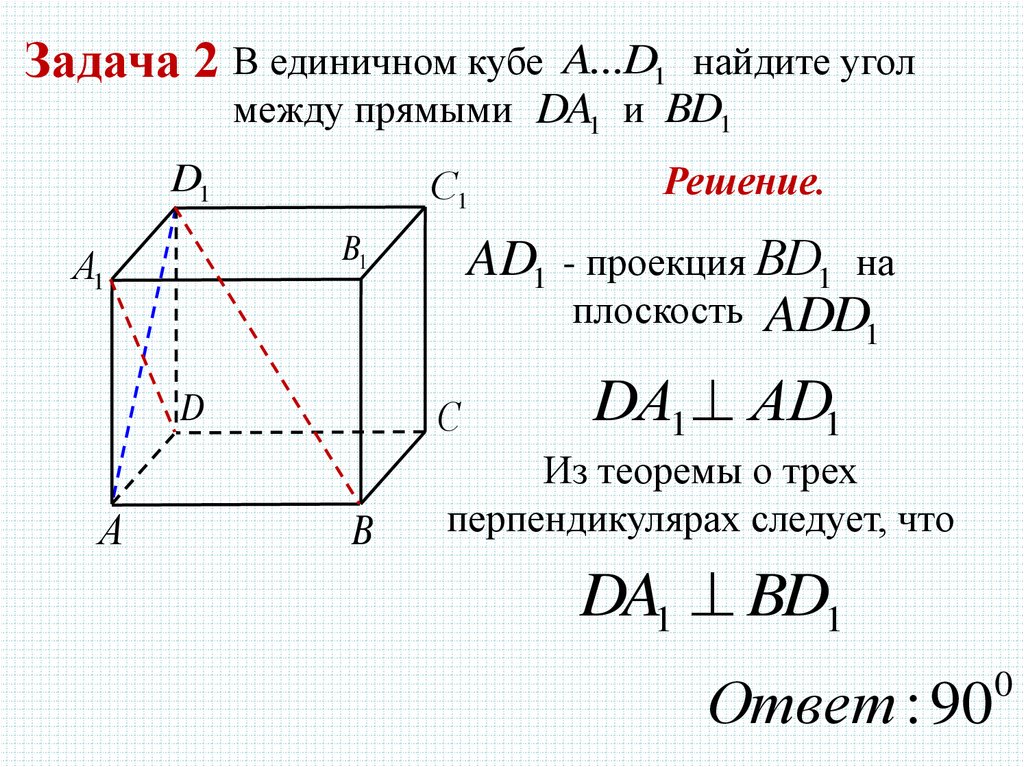
Задача 2 В единичном кубе A...D1
найдите угол
между прямыми DA1 и BD1
С1
D1
С
D
А
AD1 - проекция ВD1 на
плоскость ADD
1
B1
А1
B
Решение.
DА1 АD1
Из теоремы о трех
перпендикулярах следует, что
DA1 BD1
Ответ : 90
0

3.

Задача 3 В единичном кубе A...D1
D1
А1
найдите угол
между прямыми DA1 и D1E ,
где E – середина ребра CC1
С1
Решение.
F – середина ВВ1
B1
E
F
С
D
А
A1F || D1E DA1F
А1 AD - прямоугольный
А1 D AА1 AD 1 1 2
- прямоугольный
1 9
DF BD BF 2
4 4
2
2
А1 D 2
B
DBF
2
2
2
2
3
DF
2

4.

С1
D1
А1
B1
D
A1 F A1 B1 B1 F
2
E
F
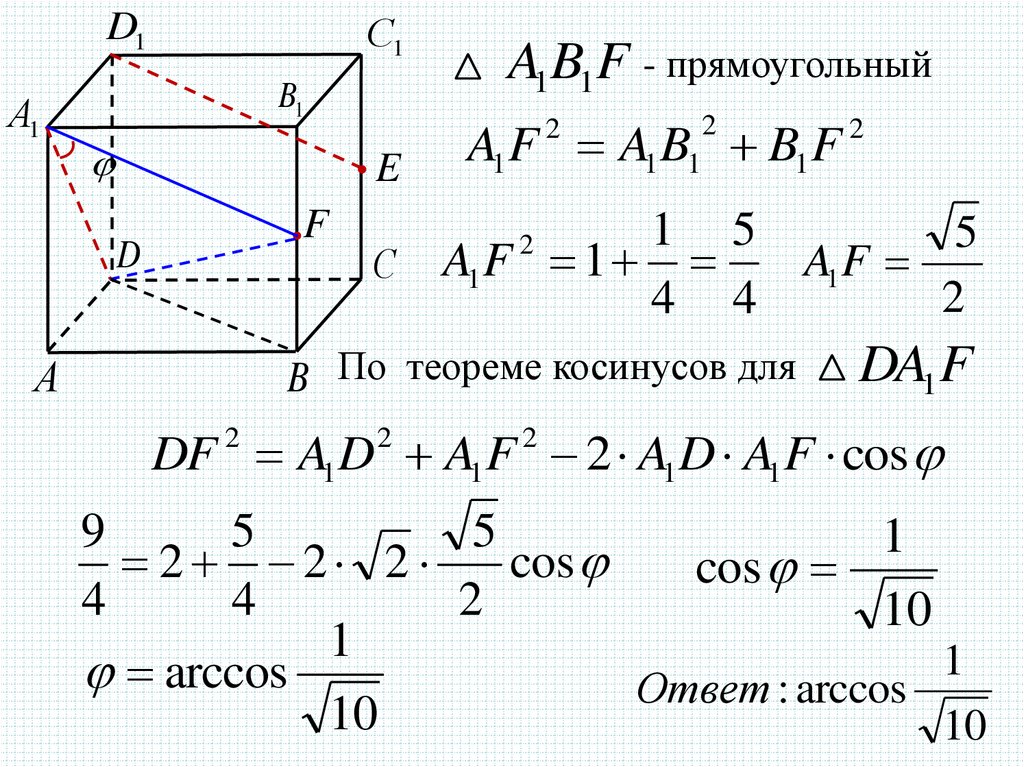
A1B1F - прямоугольный
2
1 5
5
A1 F
С A1 F 1
2
4 4
2
B По теореме косинусов для
А
2
DA1F
DF A1D A1F 2 A1D A1F cos
2
2
2
9
5
5
1
2 2 2
cos
cos
4
4
2
10
1
1
arccos
Ответ : arccos
10
10

5.

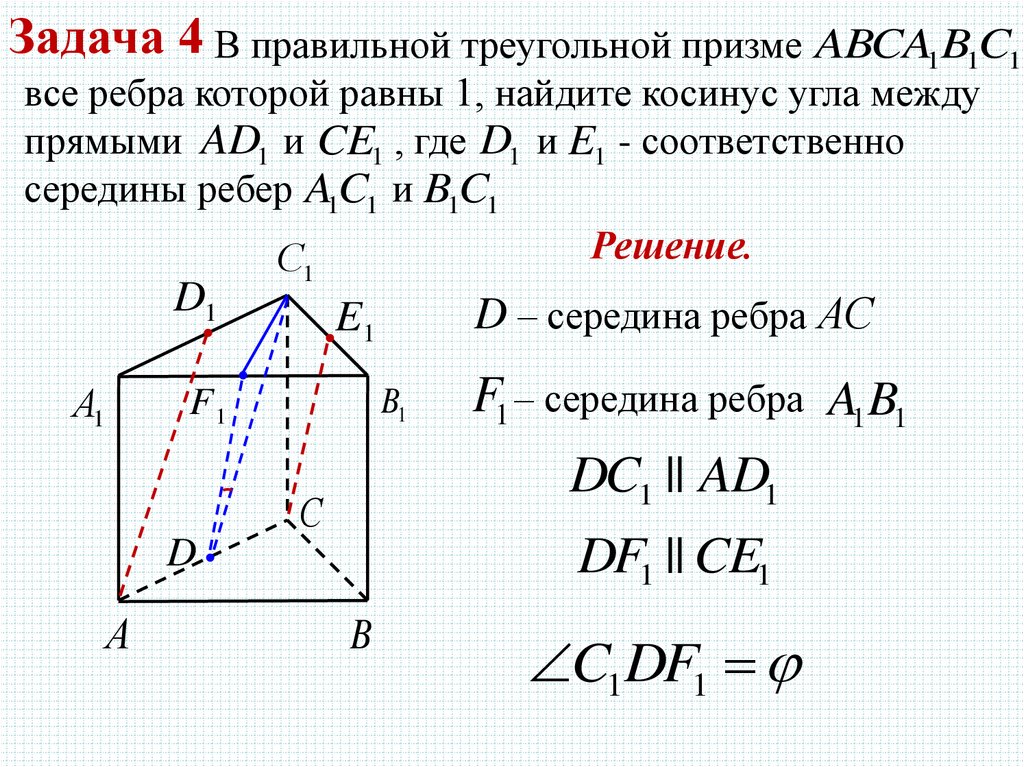
Задача 4 В правильной треугольной призме ABCA1B1C1
все ребра которой равны 1, найдите косинус угла между
прямыми AD1 и CE1 , где D1 и E1 - соответственно
середины ребер A1C1 и B1C1
Решение.
С
D1
А1
1
B1
F1
С
F1 – середина ребра A1B1
DC1 || AD1
DF1 || CE1
D
А
D – середина ребра АС
E1
B
C1DF1

6.

D1
А1
С1
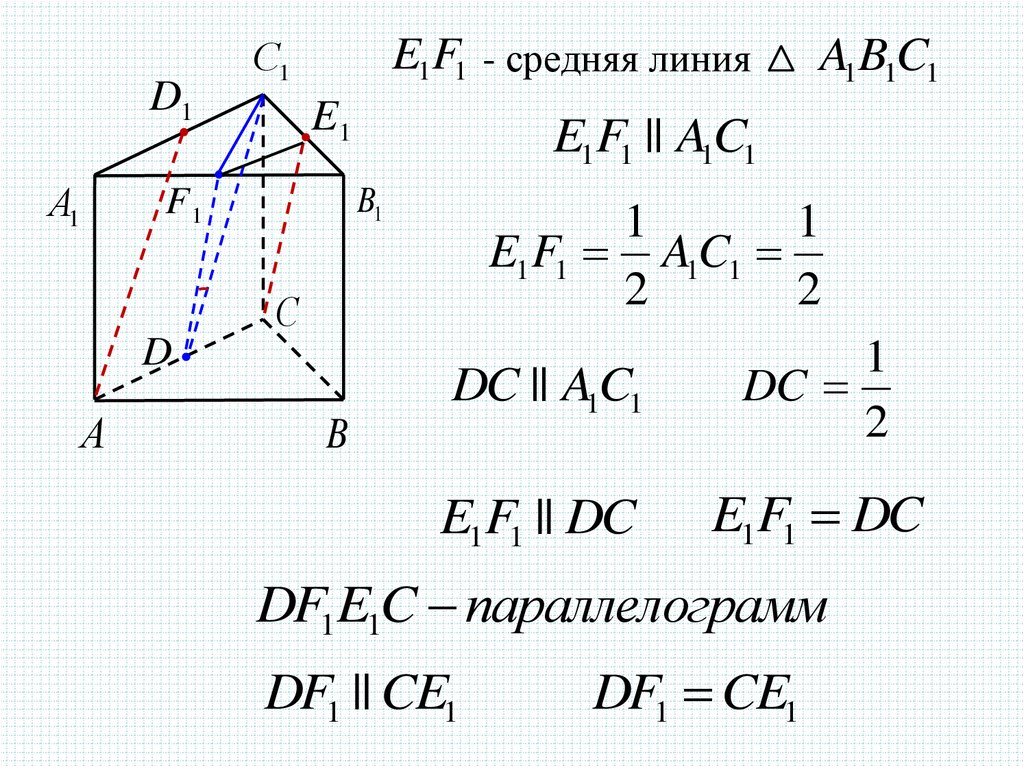
E1F1 - средняя линия
E1
E1F1 || A1C1
B1
F1
1
1
E1 F1 A1C1
2
2
С
D
А
B
A1B1C1
DC || A1C1
1
DC
2
E1F1 || DC
E1F1 DC
DF1E1C параллелограмм
DF1 || CE1
DF1 CE1

7.

D1
А1
С1
E1
1
5
B1 CE1 CC C1 E1 1
4 4
5
DF1 CE1
2
2
F1
С
D
А
CC1E1- прямоугольный
B
2
1
2
DCC1 - прямоугольный
1
5
DC1 DC CC1 1
4
4
5
DC1
2
2
2
2

8.

С1
D1
А1
A1F 1C1 - прямоугольный
E1
B1
F1
С
D
А
B
1 3
C1 F1 A1C A1 F1 1
4 4
3
C1 F1
2
2
2
1
2
По теореме косинусов для
C1DF1
C1 F1 DF1 DC1 2 DF1 DC1 cos
2
2
2
3 5 5
5 5
2
cos
4 4 4
2 2
cos 0,7
Ответ : 0,7

9.

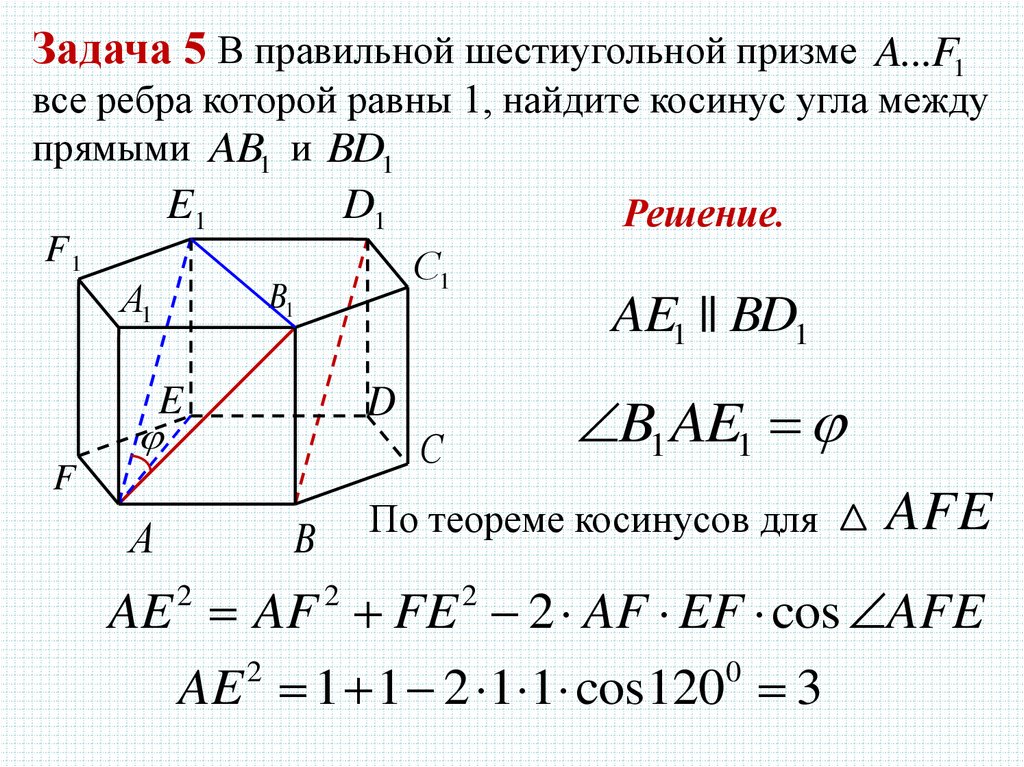
Задача 5 В правильной шестиугольной призме A...F1
все ребра которой равны 1, найдите косинус угла между
прямыми AB1 и BD1
E1
F1
А1
D1
С1
B1
AE1 || BD1
E
D
F
А
Решение.
B1 AE1
С
По теореме косинусов для
B
AFE
AE AF FE 2 AF EF cos AFE
2
0
AE 1 1 2 1 1 cos120 3
2
2
2

10.

E1
F1
А1
D1
С1
AE1 AE EE1 3 1 4
AE1 2
D
B1
E
2
2
2
B1E1 2 A1F 1 2
С
F
А
AEE1 - прямоугольный
AB1 2
B
По теореме косинусов для
B1 AE1
В1 E1 B1 A AE1 2 B1 A AE1 cos
4 2 4 2 2 2 cos
1
1
Ответ : cos
cos
2
2
2 2
2
2 2

11.

Задача 6 Длина ребра правильного тетраэдра ABCD
равна 1. Найдите косинус угла между прямыми DМ и
CL, где М – середина ребра ВС, L- середина ребра АВ.
D
Решение.
К – середина LB
MK – средняя линия
MK || CL
А
L
K
M
С
3
CL
2
B
CLB
DMK
ALC - прямоугольный
1 3
CL AC AL 1
4 4
1
3
MK CL
2
4
2
2
2

12.

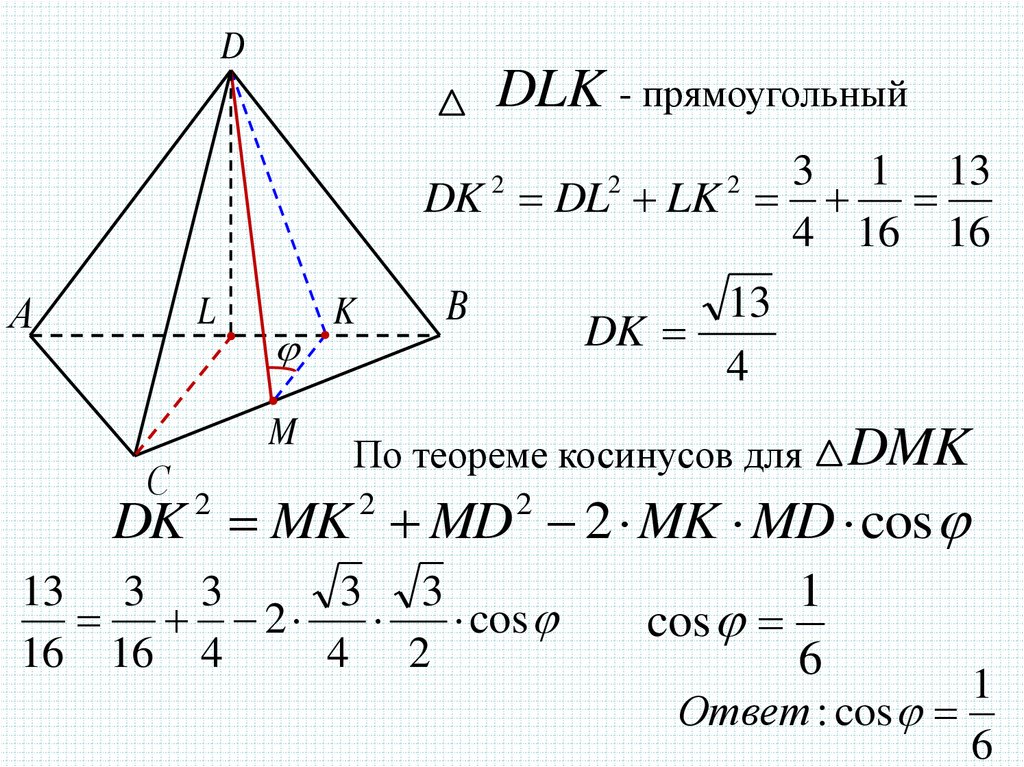
D
DLK - прямоугольный
3 1 13
DK DL LK
4 16 16
2
А
L
M
K
B
2
2
13
DK
4
DMK
С 2
2
2
DK MK MD 2 MK MD cos
По теореме косинусов для
13 3 3
3 3
2
cos
16 16 4
4 2
1
cos
6
1
Ответ : cos
6