Похожие презентации:
Угол между прямыми. Подготовка к ЕГЭ С2
1. Подготовка к ЕГЭ
С22.
Угол междупрямыми
3.
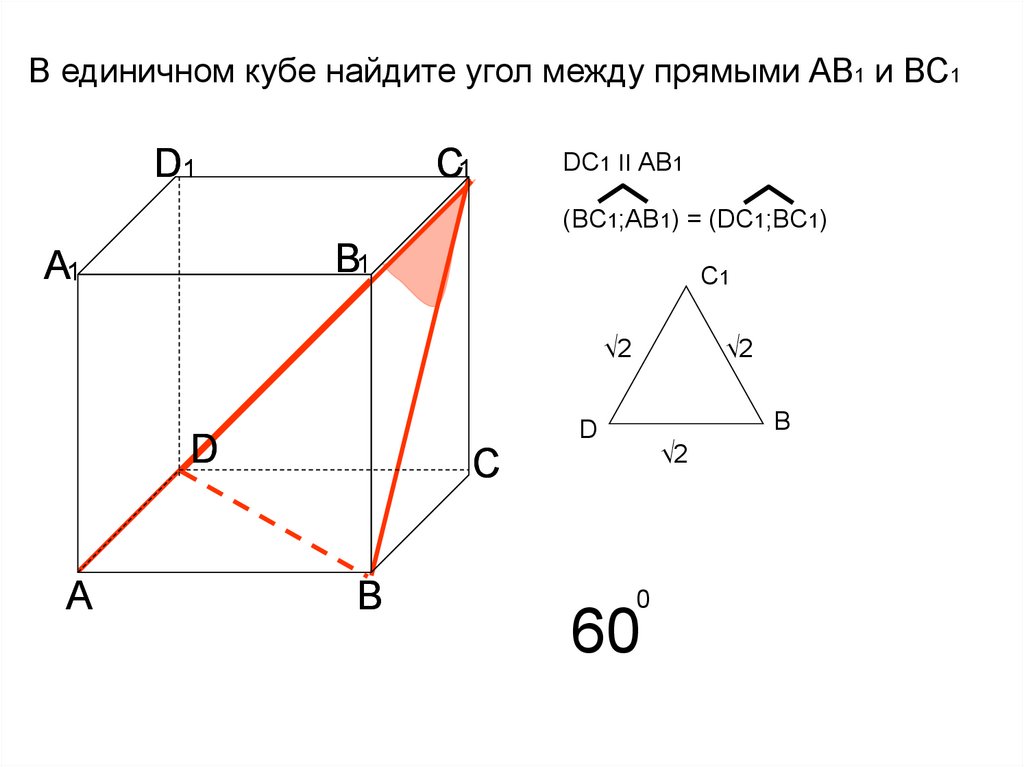
В единичном кубе найдите угол между прямыми AB1 и ВС1С1
D1
DC1 ׀׀AB1
(BC1;AB1) = (DC1;BС1)
В1
А1
С1
√2
D
А
С
В
√2
B
D
√2
0
60
4.
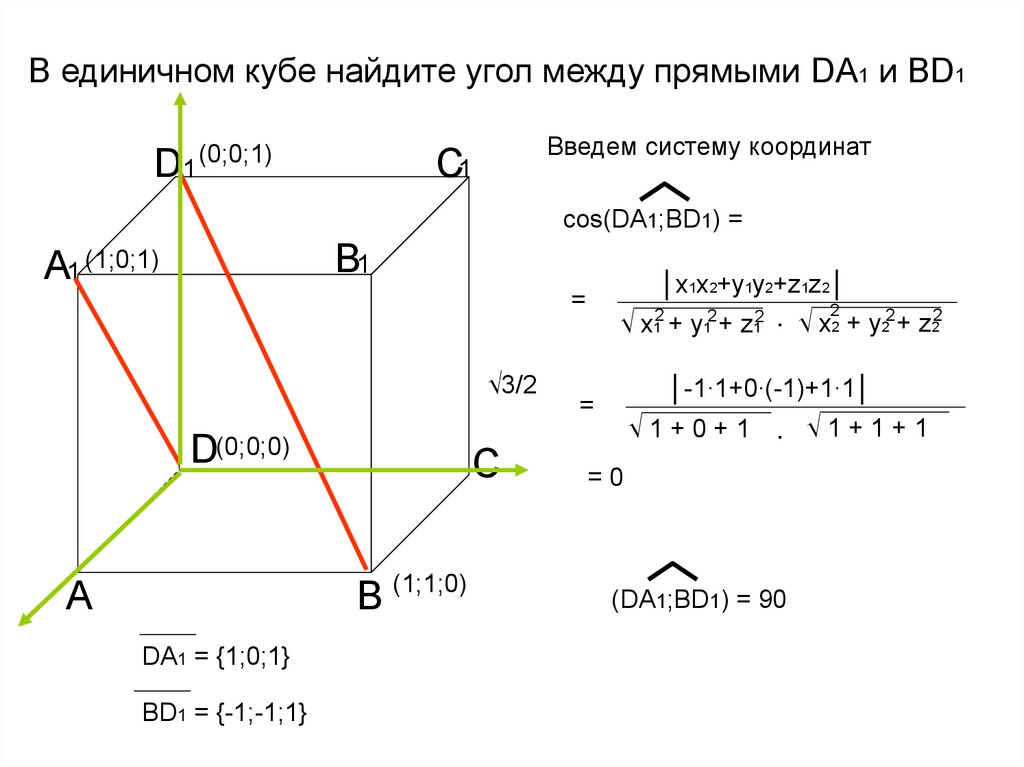
В единичном кубе найдите угол между прямыми DA1 и ВD1D1
Введем систему координат
С1
(0;0;1)
cos(DA1;BD1) =
В1
А1 (1;0;1)
│x1x2+y1y2+z1z2│
=
√3/2
D(0;0;0)
А
С
В
DA1 = {1;0;1}
BD1 = {-1;-1;1}
(1;1;0)
√ x12 + y12 + z12
.
2
√ x2 + y22 + z22
│-1∙1+0∙(-1)+1∙1│
=
√1+0+1
.
=0
(DA1;BD1) = 90
√1+1+1
5.
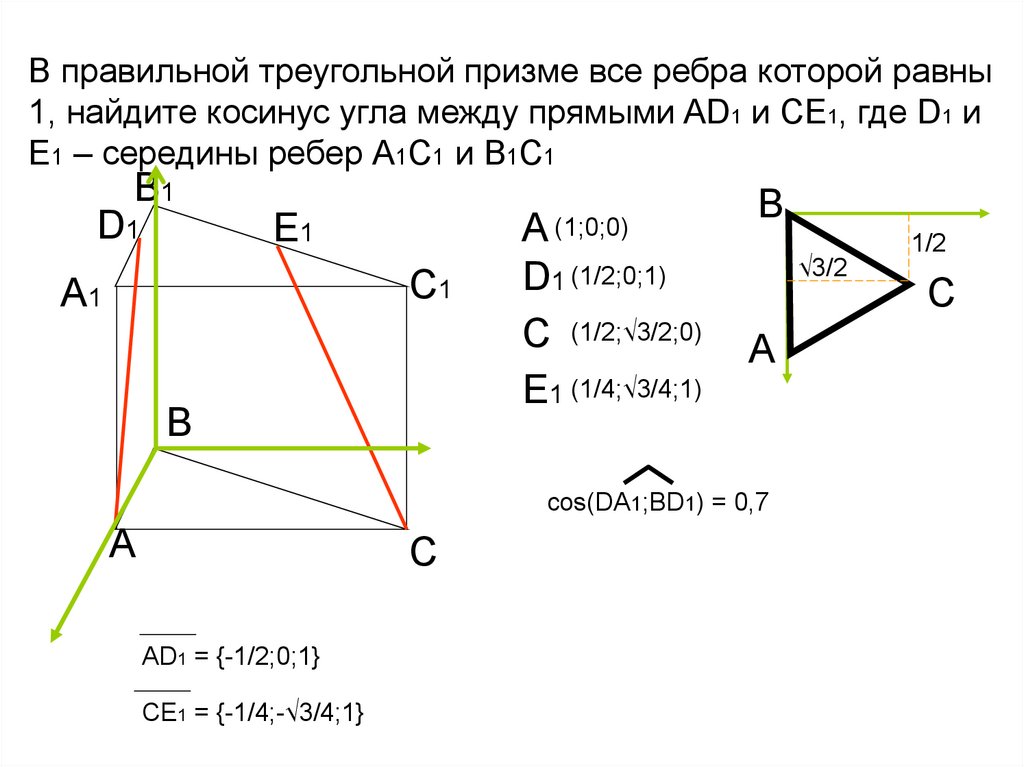
В правильной треугольной призме все ребра которой равны1, найдите косинус угла между прямыми AD1 и СЕ1, где D1 и
Е1 – середины ребер А1С1 и В1С1
В1
D1
А (1;0;0)
E1
С1
А1
В
D1 (1/2;0;1)
C (1/2;√3/2;0)
E1 (1/4;√3/4;1)
B
√3/2
А
cos(DA1;BD1) = 0,7
А
С
AD1 = {-1/2;0;1}
CE1 = {-1/4;-√3/4;1}
1/2
C
6.
В правильной треугольной призме все ребра которой равны1, найдите косинус угла между прямыми AB и СA1
В1
С1
А1
А (1;0;0)
B (0;0;0)
C (1/2;√3/2;0)
A1 (1;0;1)
В
cos(DA1;BD1) = √2/4
А
С
AB = {-1;0;0}
CA1 = {1/2;-√3/2;1}
7.
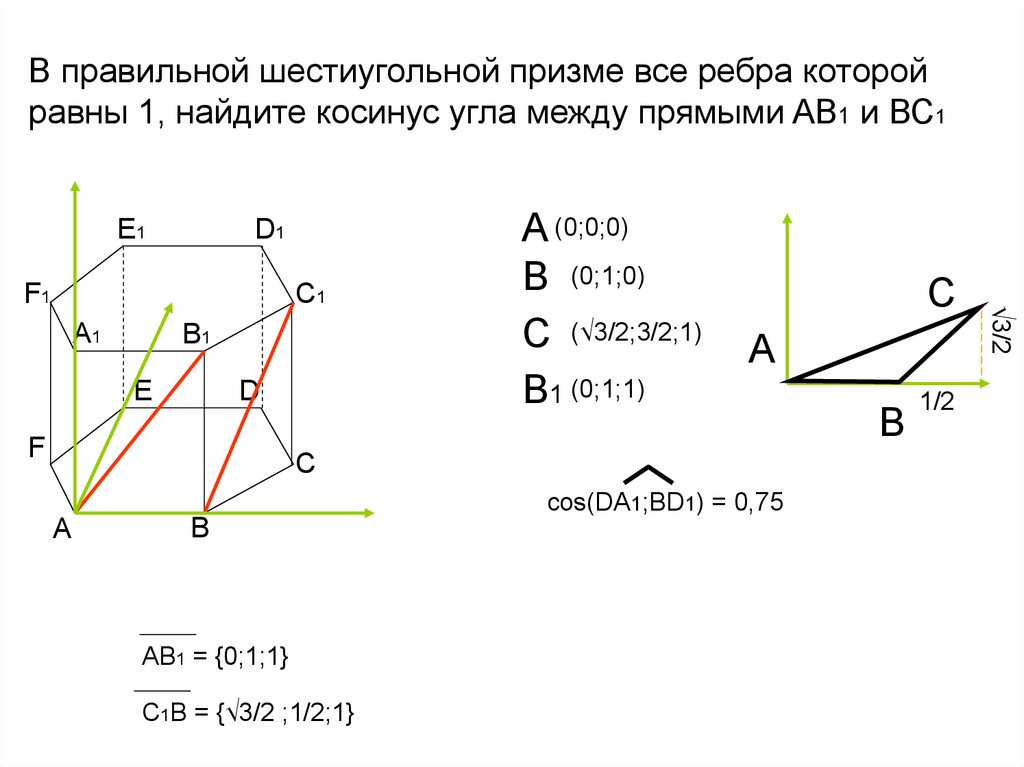
В правильной шестиугольной призме все ребра которойравны 1, найдите косинус угла между прямыми AB1 и ВС1
E1
D1
C1
А1
B1
E
D
F
C
А
C
А
cos(DA1;BD1) = 0,75
B
AB1 = {0;1;1}
C1В = {√3/2 ;1/2;1}
B
1/2
√3/2
F1
А (0;0;0)
В (0;1;0)
C (√3/2;3/2;1)
В1 (0;1;1)
8.
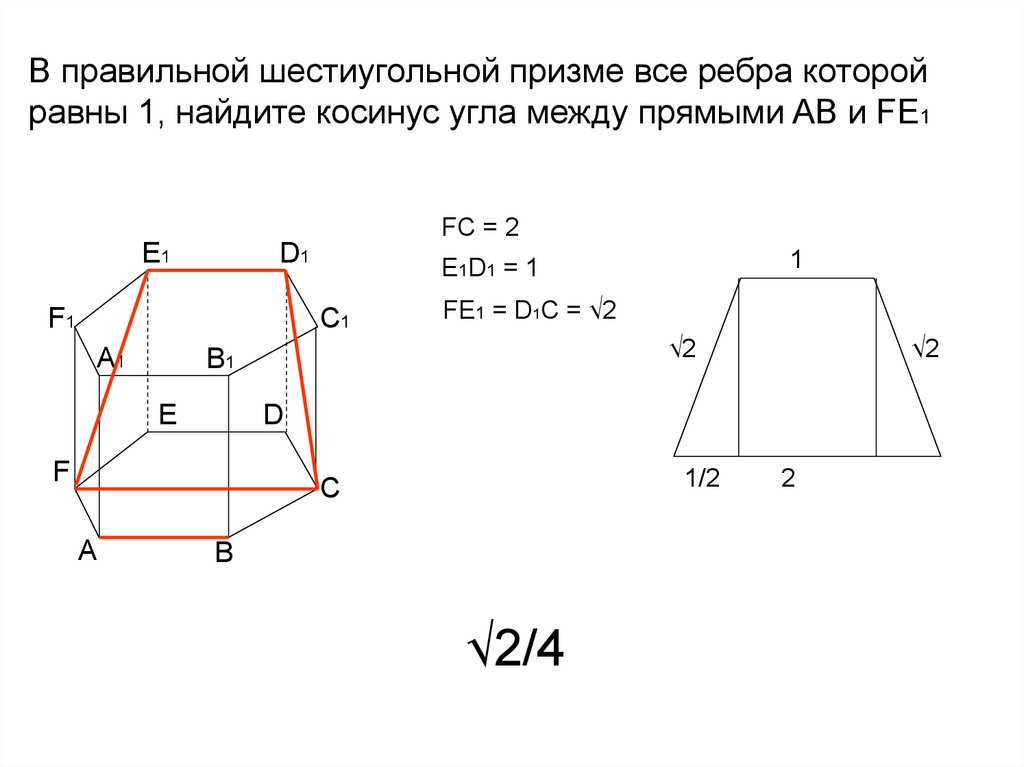
В правильной шестиугольной призме все ребра которойравны 1, найдите косинус угла между прямыми AB и FE1
FC = 2
E1
D1
F1
C1
А1
FE1 = D1C = √2
√2
B1
E
√2
D
F
1/2
C
А
1
E1D1 = 1
B
√2/4
2



 Математика
Математика








