Похожие презентации:
Первообразная. Неопределенный интеграл
1. ПЕРВООБРАЗНАЯ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
колледжверодви
н
Се
й
ки
Преподаватель ФГОУ СПО «СТК»
Якимчук Любовь Григорьевна
ех
ий т ничес
к
с
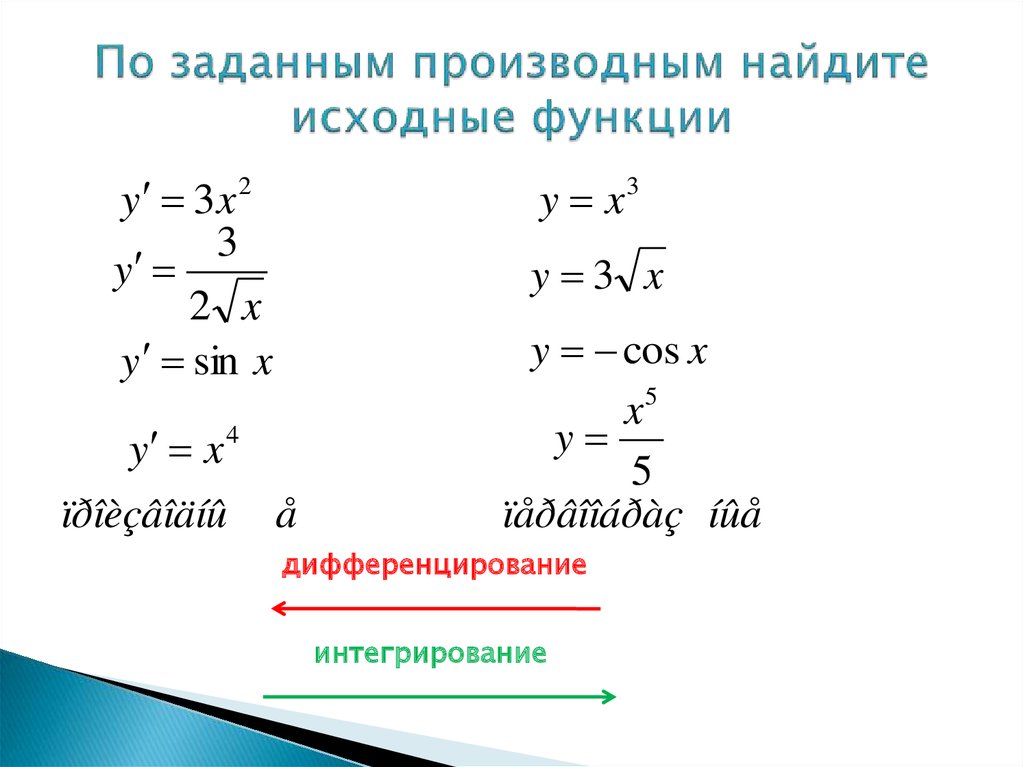
2. По заданным производным найдите исходные функции
y 3x 23
y
2 x
y sin x
y x3
y 3 x
4
y x
ïðîèçâîäíû
å
y cos x
x5
y
5
ïåðâîîáðàç íûå
дифференцирование
интегрирование
3. ПЕРВООБРАЗНАЯ
Обозначения: f x ïðîèçâîäíàÿ
F x ïåðâîîáðàç íàÿ
Функция F называется первообразной для
функции f, если выполняется условие
F x f x
4. найдите производные функций:
y x2y x 2 10
y x 2 0,5
y 2 x
y x2 3
F x x c
2
f x 2 x
совокупность первообразных
5. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Совокупность всех первообразных F(x)+cдля
функции
f(x)
называется
неопределенным
интегралом
и
обозначается
f x dx F x c
где f(x) – подинтегральная функция,
f(x)dx
–
подинтегральное
выражение
(дифференциал),
с – постоянная интегрирования.
6. Свойства неопределенного интеграла
1)k f x dx k f x dx
2)
f x g x dx f x dx g x dx
7. Немного истории
«Интеграл» - латинское словоintegro – “восстанавливать”
или integer – “целый”.
Одно из основных понятий
математического анализа,
возникшее в связи
потребностью измерять
площади, объемы, отыскивать
функции по их производным.
Впервые это слово употребил
в печати швецкий ученый Я.
Бернулли (1690 г.).
8. Немного истории
9. Лейбниц Готфрид Вильгельм (1646-1716)
« Общее искусство знаковпредставляет чудесное
пособие, так как оно
разгружает воображение…
Следует заботиться о том,
чтобы обозначения были
удобны для открытий.
Обозначения коротко
выражают и отображают
сущность вещей. Тогда
поразительным образом
сокращается работа мысли.»
Лейбниц
10.
Исаак Ньютон(1643-1727)
11.
Площадь фигурыОбъем тела вращения
Работа электрического заряда
Работа переменной силы
Центр масс
Формула энергии заряженного
конденсатора










 Математика
Математика








