Похожие презентации:
Неопределённый интеграл. Метод подстановки (замены переменной)
1. Неопределённый интеграл.
2. Метод подстановки (замены переменной)
Найтиf ( x) dx
пусть x (t ) , тогда dx t dt
f ( x) dx f (t ) (t ) dt
Функцию x (t ) следует выбирать так,
чтобы можно было вычислить неопределенный
интеграл, стоящий в правой части равенства.
3.
Замечание. Иногда целесообразнее подбиратьзамену переменного в виде t x
Пример.
x
( x) dx
пусть x t , тогда
x dx dt
x
dt
( x) dx t ln t C ln ( x) C
4. Пример 1. Вычислить интеграл
102
x
1
dx
2x 1 t
d 2 x 1 dt
2 dx dt
dt
dx
2
2 x 1
10
1 10
1 t
2 x 1
dx t dt
C
C
2
2 11
22
11
11
5. Пример 2. Вычислить интеграл
4 x 5 dx4x 5 t
d 4 x 5 dt
4 dx dt
dt
dx
5
1
2
3
2
1
1
1 t
4 x 5 dx t dt t dt C
5
5
5 3
2
2 t3
2t t
2 4 x 5 4 x 5
C
C
C
15
15
15
6. Пример 3. Вычислить интеграл
sin 2 3x dx2 3x t
d 2 3 x dt
3 dx dt
dt
dx
3
1
1
1
sin 2 3x dx 3 sin t dt 3 cos t C 3 cos 2 3x C
7. Пример 4. Вычислить интеграл
ln 5 xx dx
ln x t
d ln x dt
1
dx dt
x
6
6
ln 5 x
t
ln
x
5
x dx t dt 6 C 6 C
8. Пример 5. Вычислить интеграл
1x sin
x dx
x2
1
1
x sin
sin
x dx dx
x dx
x2
x x2
1
ln x sin t dt ln x cos t C ln x cos C
x
1
t
x
1
d dt
x
dx
2 dt
x
9. Пример 6. Вычислить интеграл
sin3
x cos x dx
sin x t
d sin x dt
cos x dx dt
4
4
t
sin x
sin x cos x dx t dt 4 C 4 C
3
3
10. Пример 7. Вычислить интеграл
dx25 4 x 2
dx
dx
25 4 x 2 52 2 x 2
1
dt
1 1
t
1
2x
2 2 arctan C arctan
C
2 5 t
2 5
5
10
5
2x t
d 2 x dt
2 dx dt
dt
dx
2
11. Пример 8. Вычислить интеграл
tan x dxsin x
tan x dx cos x dx
dt
ln t C ln cos x C
t
cos x t
d cos x dt
sin x dx dt
12. Пример 9. Вычислить интеграл
x4
x
4
t
t
e
dx
4
e
dt
4
e
C 4e C
x
t
4
x 4t
dx d 4t
dx 4 dt
e
x
4
dx
13. Пример 10. Вычислить интеграл
dxsin x
dx
sin x
sin x
2 dx
dx
2
sin x
sin x
1 cos x
dt
dt
1 t 1
1 cos x 1
2
ln
C ln
C
2
1 t
t 1 2 t 1
2 cos x 1
cos x t
d cos x dt
sin x dx dt
14. Ещё некоторые формулы.
kx b1
a
1) a kx b dx
C
k ln a
e
kx b
1 kx b
dx e
C
k
1
2) sin kx b dx cos kx b C
k
1
3) cos kx b dx sin kx b C
k
dx
1
4)
ln kx b C
kx b k
15.
dx1
5)
tan kx b C
2
cos kx b k
dx
1
6) 2
cot kx b C
sin kx b
k
7)
dx
1
n
arcsin x C
2
2 2
n
k
k n x
dx
1
n
8) 2
arctan x C
2 2
k n x
kn
k
9)
2
a
x x 2
2
2
a x dx arcsin
a x2 C
2
a 2
16. Пример 11. Вычислить интеграл
a x dx2
2
x
x a sin t t arcsin
a
dx a cos t dt
a 2 x 2 a 2 a 2 sin 2 t a 2 1 sin 2 t a 2 cos 2 t a cos t
17.
1 cos 2ta x dx a cos t a cos t dt a cos t dt a
dt
2
2
2
2
2
2
a2
a2
a2
a2 1
dt cos 2t dt t sin 2t C
2
2
2
2 2
a2
a2 1
a2
x 1
t 2 sin t cos t C arcsin x a 2 x 2 C
2
2 2
2
a 2
18. Интегралы от некоторых функций, содержащих квадратный трехчлен.
dx1. 2
ax bx c
0
2
2
b
c
b
b
c
b
2
2
2
ax bx c a x x a x 2 x
a
a
2
a
2
a
a
2
a
2
2
2
b
c
b
b
2
a x 2 a x k
2a a 4a
2a
k
19.
dx1
dx
1
dt
ax 2 bx c a b 2 2 a t 2 k 2
x
k
2a
b
x
t
2a
dx dt
табличный интеграл
20.
02.
dx
ax bx c
2
2
2
b
c
b
b
c
b
2
2
2
ax bx c a x x a x 2 x
a
a
2
a
2
a
a
2
a
2
2
2
b
c
b
b
2
a x 2 a x k
2a a 4a
2a
k
21.
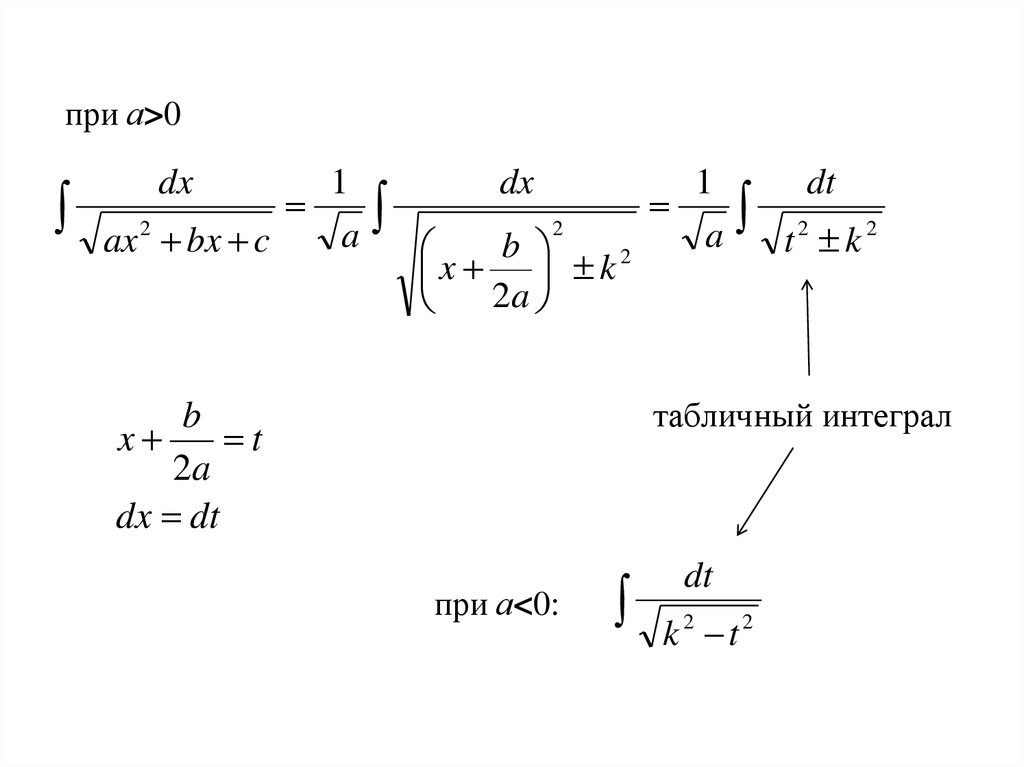
при а>0dx
1
2
a
ax bx c
dx
2
b
2
x k
2a
1
a
dt
t2 k2
табличный интеграл
b
x
t
2a
dx dt
при а<0:
dt
k2 t2
22. Пример 12. Вычислить интеграл
dxx2 2x 5
x 2 2 x 5 x 2 2 x 1 5 1 x 1 4
2
dx
dx
dt
1
t
2
arctan C
2
2
2
x 2x 5
2
x 1 4 t 2 2
x 1 t
dx dt
1
x 1
arctan
C
2
2
23. Пример 13. Вычислить интеграл
dx2
11 10 x x
11 10 x x 2 ( x 2 10 x 11) ( x 2 10 x 25 11 25)
x 5
2
36
dx
dx
dt
1 t 6
2 2 ln
C
2
2
11 10 x x
t 6
12 t 6
x 5 36
x 5 t
dx dt
1
x 5 6
1
x 11
ln
C ln
C
12 x 5 6
12
x 1
24. Пример 14. Вычислить интеграл
dxx 2 6 x 10
x 6 x 10 x 6 x 9 10 9 x 3 1
2
2
2
dx
x 2 6 x 10
x 3 t
dx dt
dx
x 3 2 1
dt
2
ln
t
t
1 C
2
t 1
ln x 3 x 2 6 x 10 C
25. Пример 15. Вычислить интеграл
dx5 4x x2
5 4 x x 2 ( x 2 4 x 5) x 2 4 x 4 5 4
x 2 9 9 x 2
dx
5 4x x
2 x t
dx dt
2
dx
3 2 x
2
2
2
dt
2
t
arcsin C
2
2
3
3 t
2 x
arcsin
C
3














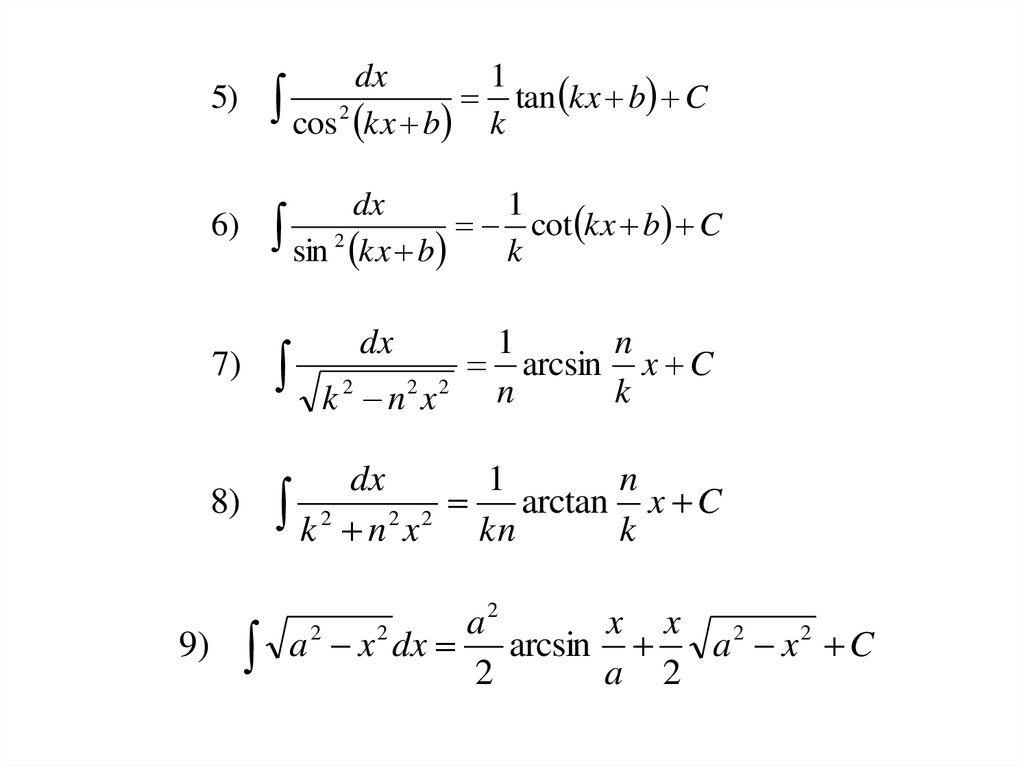

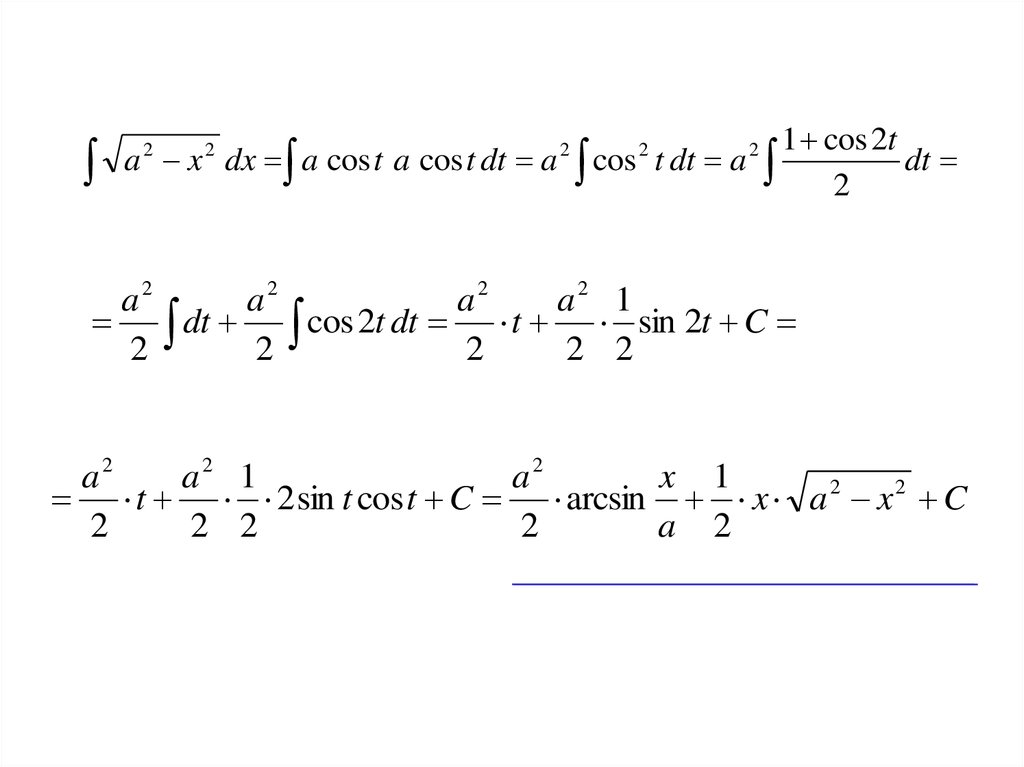







 Математика
Математика








