Похожие презентации:
Автокорреляция и её последствия
1. Лекция 5 Автокорреляция
1. Автокорреляция и еёпоследствия
2. Обнаружение автокорреляции
3. Оценка коэффициентов при автокорреляции
2. 1. Автокорреляция и её последствия
В классической модели считается, чтовыполняется предпосылка 4° МНК и
значение случайной величины i не зависит
от значений возмущений j в других
наблюдениях, т.е. M ( i j ) 0 при i j .
В практических задачах это условие
может не выполняться.
3.
Автокорреляция определяется как корреляционная зависимость между значениямиодного показателя, упорядоченными в
пространстве или во времени (временные
ряды).
Автокорреляция случайной составляющей i - это корреляционная зависимость i
со значениями этой же составляющей в
других наблюдениях i l . Величину l (величину сдвига) во временных рядах называют
лагом. При l 1 речь идёт о соседних наблюдениях.
4.
Различают положительную и отрицательную автокорреляцию.В качестве примера проанализируем модель зависимости спроса на мороженное y
(по ежемесячным данным) от доходов x
в предположении, что состояние погоды
будет единственным фактором, "скрытым"
в переменной .
Очевидно, что будет несколько последовательных наблюдений, когда теплая погода
способствует увеличению спроса на мороженое и, следовательно, значения будут
положительные.
5.
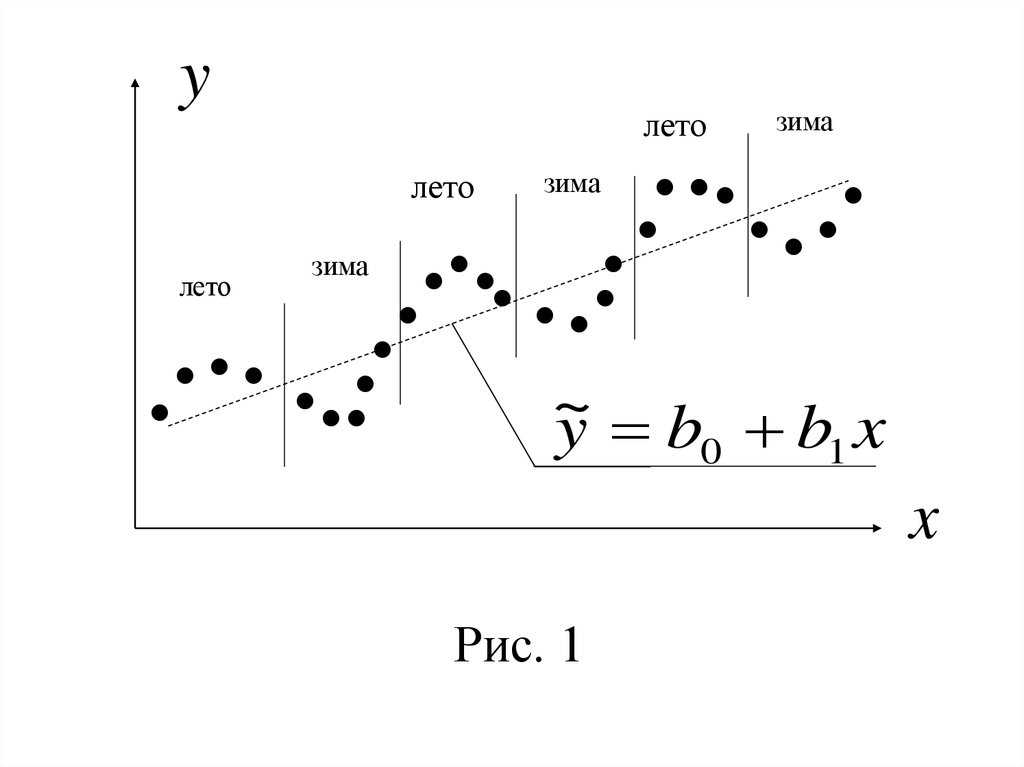
После этого будут несколько последовательных наблюдений, когда при холодной погоде ситуация будет складываться противоположным образом (рис. 1).6.
yлето
лето
лето
зима
зима
зима
~
y b0 b1 x
x
Рис. 1
7.
Из рисунка видно, что имеются зоны, гденаблюдаемые значения yi оказываются выше
~
yi и зоны,
объясненного значения
(лето)
где они располагаются ниже линейной линии
регрессии (зима).
Такие чередующиеся зоны графически
выражают положительную автокорреляцию.
8.
Отрицательная автокорреляция встречаетсяв тех случаях, когда последовательные наблюдения действуют друг на друга по принципу "маятника" - завышенные значения yi по
сравнению с ~yi в предыдущем наблюдении
приводят к занижению их в последующем
наблюдении и наоборот (рис. 2).
9.
y~
y b0 b1 x
x
Рис. 2
10.
В экономике отрицательная корреляциявстречается достаточно редко.
Последствия автокорреляции в некоторой
степени сходны с последствиями гетероскедастичности: оценки b j коэффициентов
модели перестают быть эффективными,
значения t статистик – завышенными,
дисперсии оценок D (b j ) являются
смещенными.
11. 2. Обнаружение автокорреляции
Для обнаружения автокорреляции в первую очередь можно использовать наиболеепростой графический способ. Оценкой
~
составляющей i является остаток ei yi yi .
Отсюда если корреляция ошибок регрессии не равна нулю, то она присутствует и в
остатках регрессии.
12.
В соответствии с предпосылками МНКостатки e i должны быть случайными, что на
графике координатной плоскости i 0 e
( i номер наблюдения) выглядит "облаком,
проткнутым " осью абсцисс i (рис. 3).
13.
eiРис. 3
i
14.
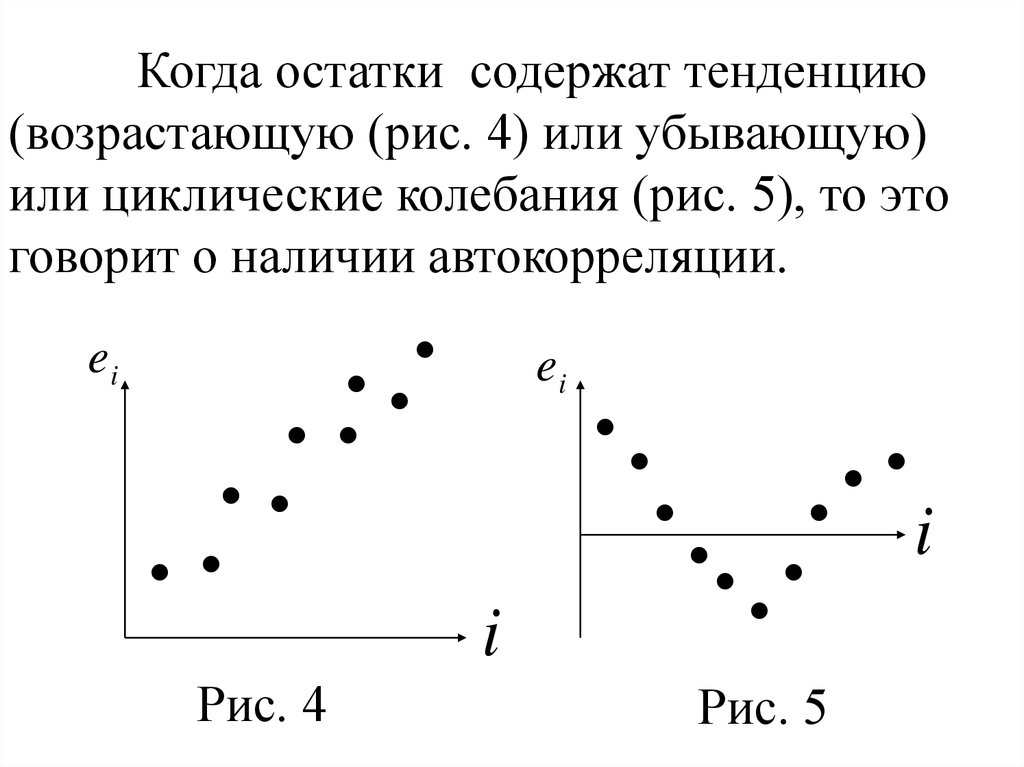
Когда остатки содержат тенденцию(возрастающую (рис. 4) или убывающую)
или циклические колебания (рис. 5), то это
говорит о наличии автокорреляции.
ei
ei
i
Рис. 4
Рис. 5
i
15.
Для обнаружения автокорреляциииспользуют также статистические тесты.
Наиболее распространенным является
критерий Дарбина-Уотсона. Этот тест
используется для обнаружения автокорреляции первого порядка, когда автокорреляция подчиняется уравнению
i i 1 i
где i случайная составляющая,
удовлетворяющая предпосылкам МНК.
(1)
16.
Это означает, что величина случайноговозмущения в любом наблюдении равна его
значению в предыдущем наблюдении,
умноженному на , плюс новое возмущение i . Данная схема называется
авторегрессией, поскольку определяется
значением той же самой величины i с
запаздыванием. Так как запаздывание здесь
равно 1, то уравнение (1) называют
авторегрессией 1-го порядка.
17.
Если 0 , то автокорреляция положительна, а при 0 - отрицательна. При 0автокорреляция отсутствует.
Критерий Дарбина-Уотсона сводится к
проверке гипотезы H 0 : 0 .
Для проверки гипотезы используется
n
статистика
(e e ) 2
d
i 2
i 1
i
n
e
i 1
,
2
i
которую так и называют статистикой
Дарбина-Уотсона.
(2)
18.
Нетрудно показать, что для большихвыборок справедливо равенство
d 2(1 r1 ),
(3)
где r1 выборочный коэффициент корреляции
между соседними возмущениями, определяn
емый по формуле
r1
e e
i 2
n
i i 1
e
i 1
2
i
.
19.
Если корреляция отсутствует, то r1 0, исогласно выражению (3) величина d
должна быть близка к 2. При r1 1
величина d 0 и это означает положительную автокорреляцию. Если же r1 1,
то d 4 и это говорит об отрицательной
автокорреляции.
20.
Критическое значение статистики d зависитот числа p факторов модели, от объема
выборки n и, к сожалению, от конкретных
значений объясняющих переменных.
Поэтому невозможно составить таблицу
критических точек статистики d , как это
можно было сделать для t и F статистик.
21.
Но можно вычислить критическуюверхнюю d в и критическую нижнюю d н
границы для критерия d , которые зависят
только от объёма выборки n , числа p
факторов модели и уровня значимости .
В итоге алгоритм применения теста
Дарбина-Уотсона следующий:
выдвигается гипотеза
вии автокорреляции;
H0
об отсутст-
22.
по формуле (2) или (3) находитсяфактическое значение d ;
по специальным таблицам ДарбинаУотсона определяются значения d в и d н по
известным числам n , p и ;
по этим значениям числовой промежуток 0,4 изменения d разбивается на
пять интервалов (рис. 6):
23.
00
Зона
0
неопред
еленнос
ти
dн
Зона
неопред
еленнос
ти
dв
2
Рис. 6
4 dв
0
4 dн
d
4
24.
в зависимости от того, в какой интервал попадает фактическое значение dделается вывод об автокорреляции. Если d
попадает в зону неопределенности, то тест
не даёт ответа об автокорреляции.
Описанный тест
обладает
следующими недостатками:
тест можно использовать только для тех
моделей, которые имеют свободный член;
25.
тест проверяет только автокорреляциюпервого порядка;
тест даёт достоверные результаты
только при больших выборках;
наличие в тесте зон
неопределенности.
26. 3. Оценка коэффициентов при автокорреляции
Рассмотрим основной подход к оценкепараметров регрессии для случая, когда
имеется автокорреляция на примере парной линейной регрессии вида
yi 0 1 xi i . (4)
Для предыдущего наблюдения модель
запишется
yi 1 0 1 xi 1 i 1. (5)
27.
Будем считать автокорреляцию первогопорядка (1) и коэффициент корреляции
известным.
Умножим на него уравнение (5) и вычтем
результат почленно из уравнения (4)
yi yi 1 (1 ) 0 1 ( xi xi 1 ) ( i i 1 )
28.
Сделав замену переменныхyi yi yi 1 , xi xi xi 1 , (6)
0 0 (1 ), i i i 1 ,
получим в силу (1)
yi 0 1 xi i
7
где i случайная составляющая,
удовлетворяющая предпосылкам МНК.
Поэтому оценка параметров уравнения (7)
может быть выполнена обычным МНК
29.
Отсюда схема метода:преобразовать исходные переменные по
формулам (6) для i 2, n ;
применив обычный МНК к уравнению
(7), определить оценки b0 , b1 коэффициентов
этого уравнения;
вычислить оценку b0 по формуле
b0
b0
;
1
30.
записать оценку исходного уравнения~
y b0 b1 x.
Видно, что такой способ преобразования
переменных приводит к потере первого наблюдения. Это уменьшает на единицу число
степеней свободы и при малых объёмах
представляет чувствительную потерю. В этих
случаях первое наблюдение восстанавливают
с помощью поправки Прайса-Уинстона:
31.
x1 1 2 x1 ,y1 1 2 y1. (8)
Основная идея метода основывается на знании . Но на практике этот коэффициент
неизвестен. Существуют различные методы
его оценки. Например, оценку можно найти
с использованием статистики ДарбинаУотсона
r 1 d / 2.
32.
Другой подход, называемый методомКохрана-Оркатта, представляет следующий
итерационный процесс:
1. Оценивается регрессия (4) с исходными непреобразованными данными.
2. Вычисляются остатки ei yi ~yi .
3. Оценивается регрессионная зависимость e i от ei 1 , соответствующая формуле
ei r ei 1 i
где r оценка .
33.
4. С найденным значением r уравнение (4)преобразуется в уравнение (7), оценивание
которого позволяет получить пересмотренные оценки b0 , b1 коэффициентов 0 , 1 , а
затем вычислить и b0 , b1 .
5. Повторно вычисляются остатки e i и
процесс возвращается к пункту 3 алгоритма.
Чередование этапов пересмотра оценок b0 , b1
и оценки r продолжается до тех пор, пока
оценки на последнем и предпоследнем цикле
не совпадут с заданной степенью точности.































 Математика
Математика








