Элементы теории вероятностей и статистики. Решение задач на проверку статистических гипотез

1. Тема 1. Элементы теории вероятностей и статистики Решение задач на проверку статистических гипотез

2.

Проверка гипотезы о мат. ожидании
нормальной СВ при известной дисперсии
1) X
2)
~ N m,
x m0
U
/ n
H 0 : m m0
U ~ N 0,1
1
I) H1 : m m0
u
/ 2
u
критич
НОРМСТОБР (1 )
2

3.

Проверка гипотезы о мат. ожидании
нормальной СВ при известной дисперсии
| U набл | u / 2
| U набл | u / 2
H0
1
H1

4.

Проверка гипотезы о мат. ожидании
нормальной СВ при известной дисперсии
2
H1 : m m0
II)
u
1
НОРМСТОБР (1 )
III)
u
U набл u H 0
U набл u1
1
3
H1 : m m0
НОРМСТОБР ( )
U набл u
U набл u
H0

5.

n=100,
Задача №1
X~N(m, 5), x 26,5 0,05
Проверить гипотезы:
1
1) H 0 : m m0 25, H1 : m m0 25
1
2) H 0 : m m0 25, H1 : m m0 25
3) H 0 : m m0 25,
1
H1 : m m0 25
Решение:
1. Вычисляем набл. значение стат. критерия
x m0
U
/ n

6.

2. Вычисление критической точки СНЗР
для двусторонней критической области
2
2
U kp
uкр
U
U kp
1
u / 2 Ф u / 2
2
U kp НОРМСТОБР (1 -
2
)

7.

Задача №1
3. Принятие решения
| U набл | uкр
| U набл | uкр
H0
1
H1

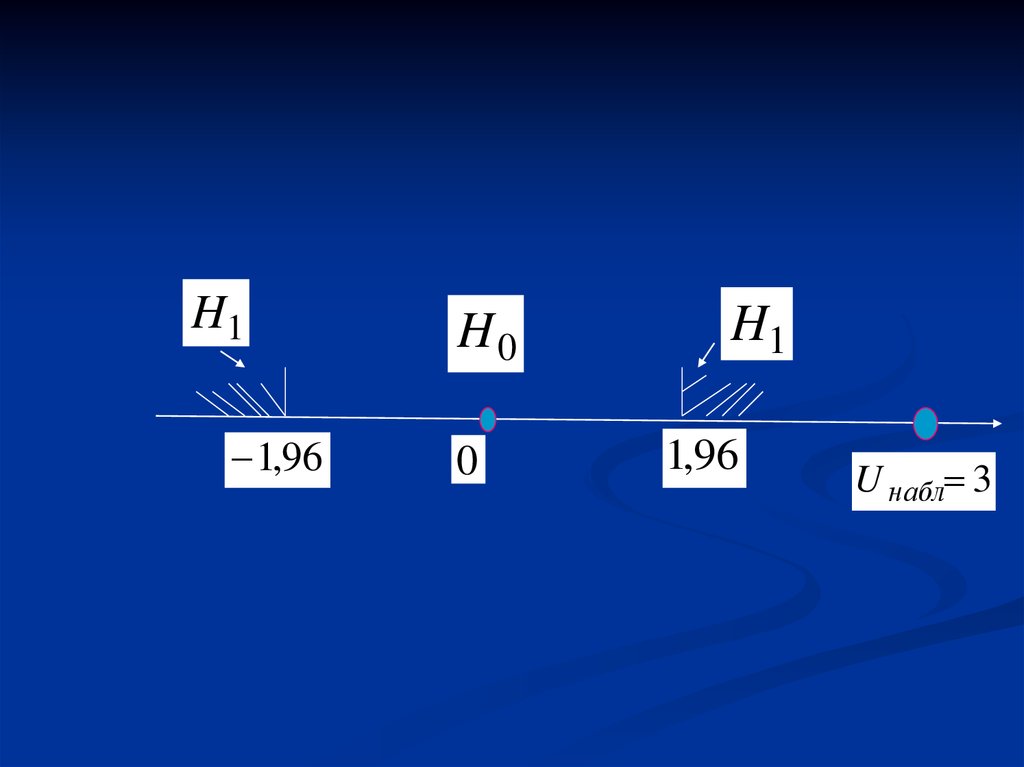
8.

H1
1,96
H0
0
H1
1,96
U набл 3

9.

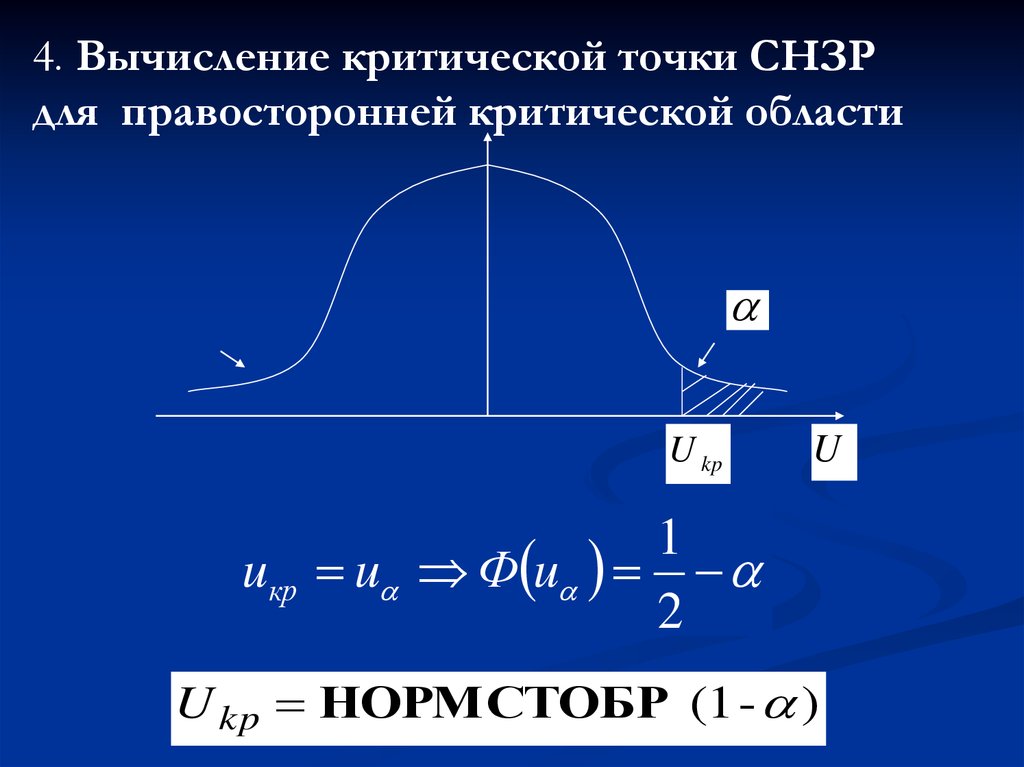
4. Вычисление критической точки СНЗР
для правосторонней критической области
U kp
U
1
uкр u Ф u
2
U kp НОРМСТОБР (1 - )

10.

Задача №1
5. Принятие решения
U набл u H 0
U набл u H
1

11.

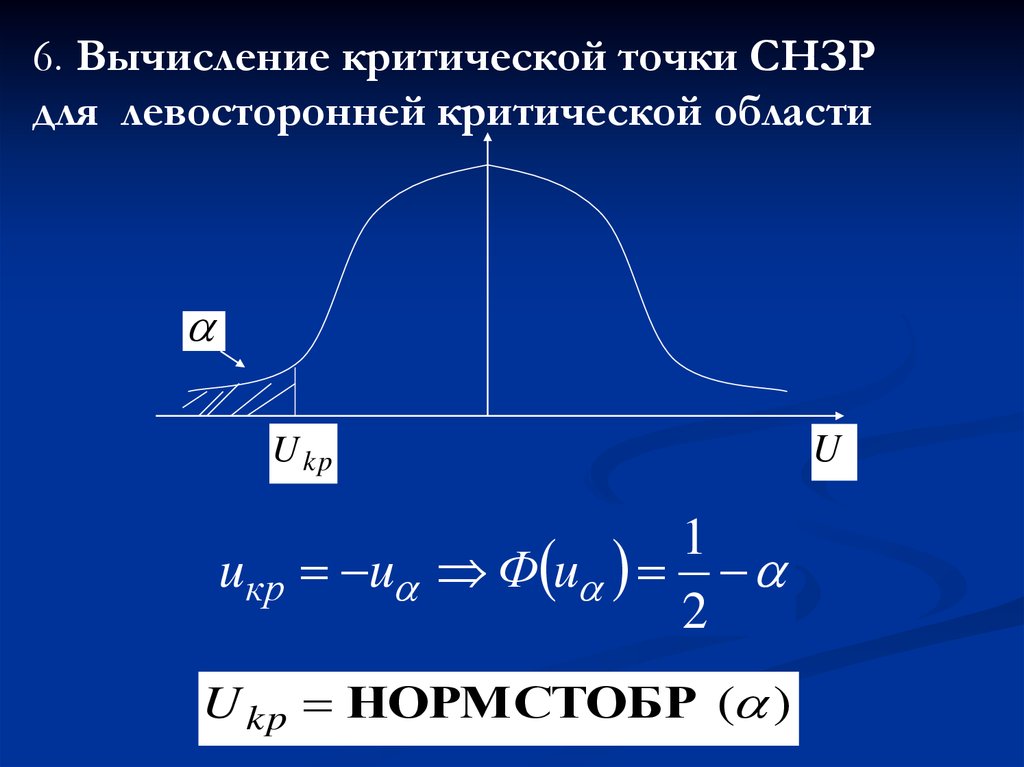
6. Вычисление критической точки СНЗР
для левосторонней критической области
U kp
uкр
1
u Ф u
2
U kp НОРМСТОБР ( )
U

12.

7. Принятие решения
U набл u H 0
U набл u H1

13.

Проверка гипотезы о мат. ожидании
нормальной СВ при неизвестной дисперсии
1) X
~ N m, H 0 : m m0
x m0
2) T
s/ n
1
3) H1 : m m0
t / 2, n 1 СТЬЮДРАСПО БР ( ; n 1)
x m0
| Tнабл |
t / 2, n 1
s/ n
| Tнабл | t / 2, n 1
H0
H1

14.

Проверка гипотезы о мат. ожидании
нормальной СВ при неизвестной дисперсии
2
: m m0 t , n 1 СТЬЮДРАСПО БР(2 ; n 1)
Tнабл t , n 1 H 0
Tнабл t , n 1 H1
3
5) H1 : m m0
4) H1
t 1 , n 1 t , n 1 СТЬЮДРАСПО БР (2 ; n 1)
Tнабл t , n 1 H 0
Tнабл t , n 1
H1

15.

n=16,
Задача №2
X~N(m, σ), x 12,4 S 1,2
0,05
1
1) H 0 : m m0 11,8 H1 : m m0 11,8
Проверить гипотезы:
2)
1
H 0 : m m0 11,8 H1 : m m0 11,8
Решение:
1. Вычисляем набл. значение стат. критерия
x m0
T
S/ n

16.

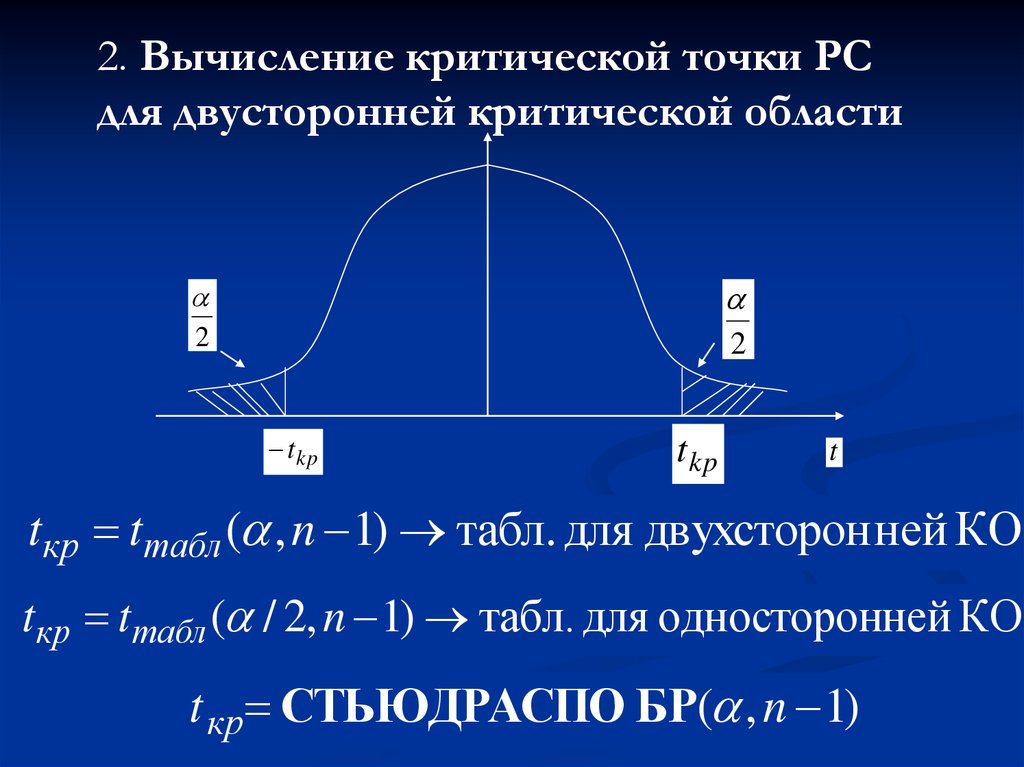
2. Вычисление критической точки РС
для двусторонней критической области
2
2
t kp
t kp
t
tкр tтабл ( , n 1) табл. для двухсторон ней КО
tкр tтабл ( / 2, n 1) табл. для односторонней КО
t кр СТЬЮДРАСПО БР( , n 1)

17.

3. Принятие решения
| Tнабл | tкр
| Tнабл | t кр
H0
H1

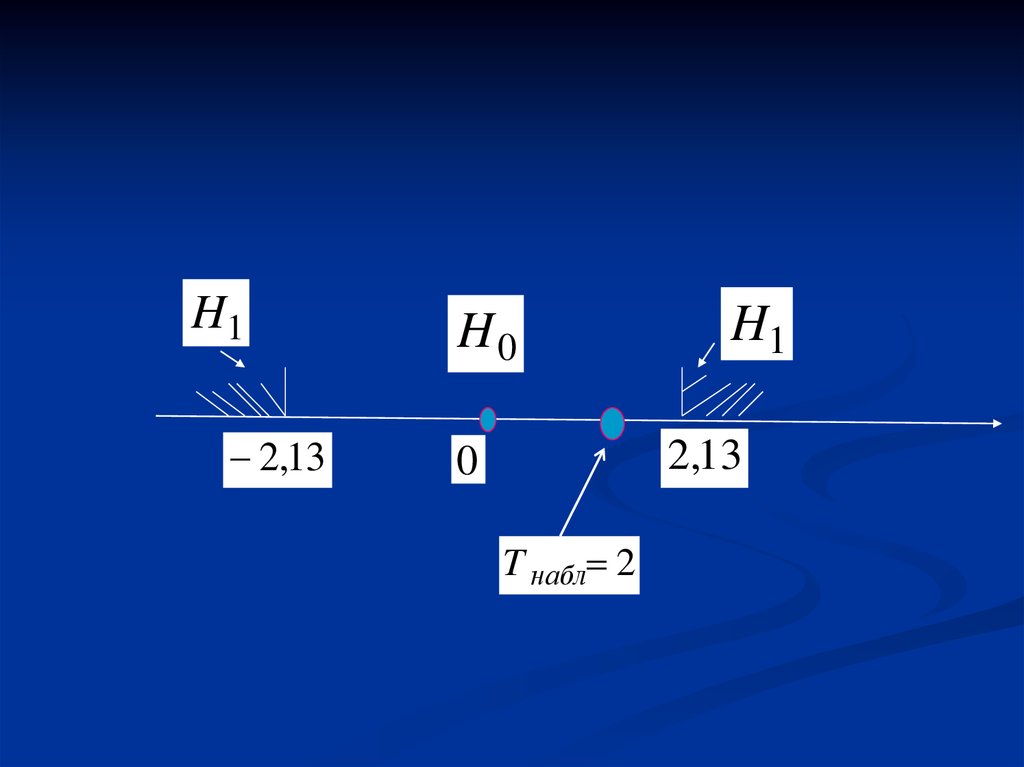
18.

H1
2,13
H0
H1
2,13
0
T набл 2

19.

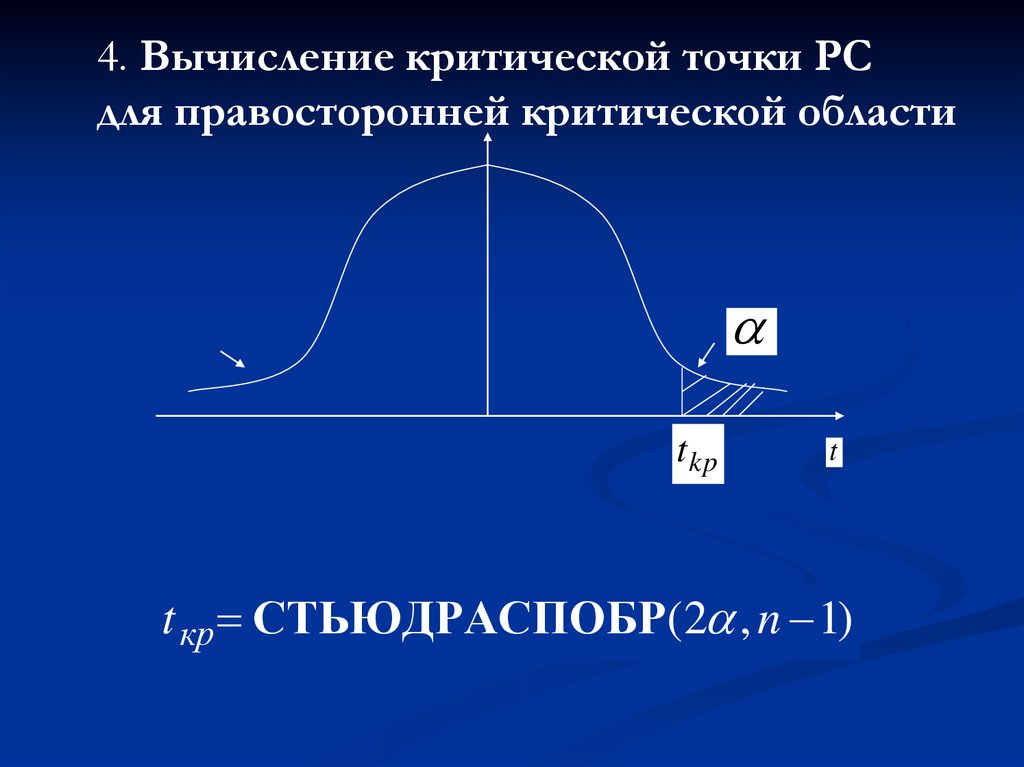
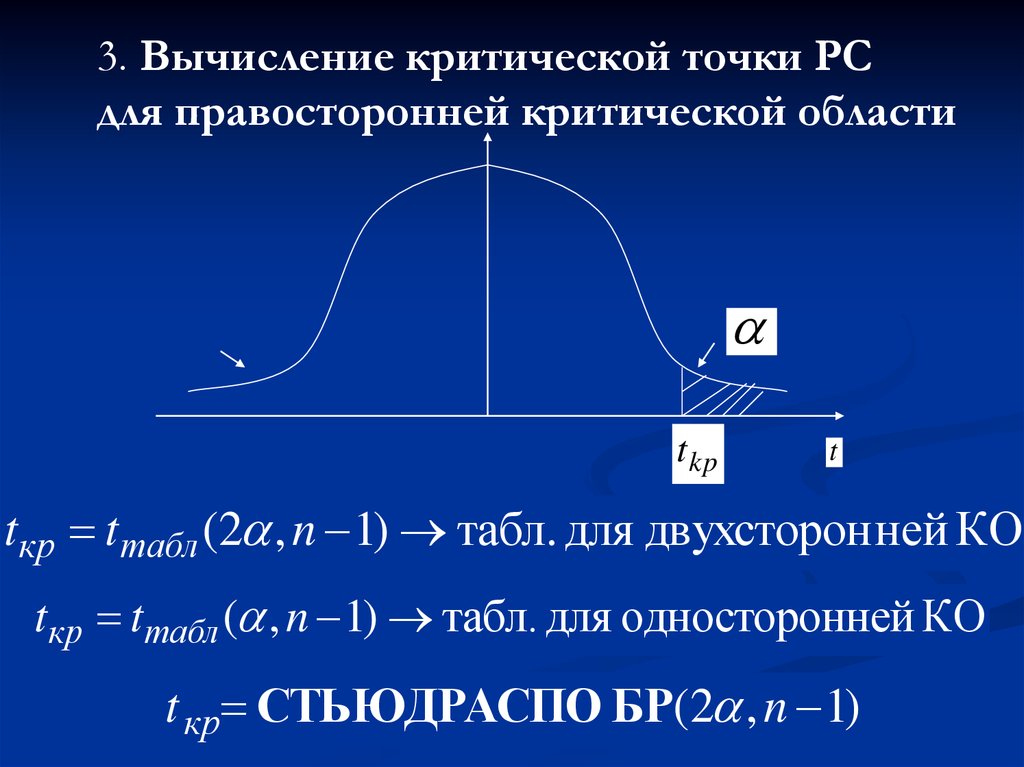
4. Вычисление критической точки РС
для правосторонней критической области
t kp
t
t кр СТЬЮДРАСПОБР(2 , n 1)

20.

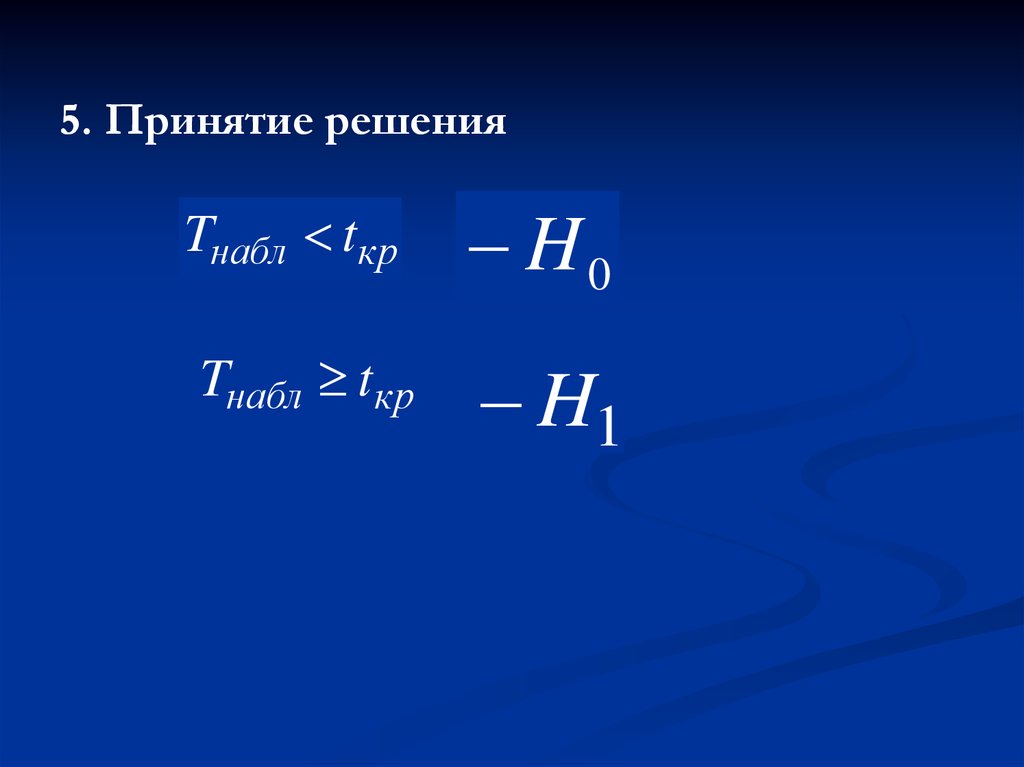
5. Принятие решения
Tнабл tкр
Tнабл tкр
H0
H1

21.

Проверка гипотезы о величине дисперсии
нормальной СВ
1)X
~ N m,
2)
3)
2
n 1 S
H0 :
2
0
2
2
0
1
2
H1 :
2
2
0
1 / 2, n 1 / 2, n 1 H 0
ХИ 2ОБР 1 / 2, n 1 ХИ 2ОБР / 2, n 1
2
2
набл
2
набл
2

22.

Проверка гипотезы о величине дисперсии
нормальной СВ
2
набл
1 / 2, n 1 H
2
набл
2
/ 2, n 1
2
H
1
1

23.

Проверка гипотезы о величине дисперсии
нормальной СВ
2
H1 :
4)
2
2
0
, n 1 ХИ 2ОБР ( ; n 1)
2
2
набл
, n 1
H0
2
набл
, n 1
H1
2
2

24.

Проверка гипотезы о величине дисперсии
нормальной СВ
3
H1 :
2
1 , n 1 ХИ 2ОБР (1 ; n 1)
5)
2
2
0
2
набл
1 , n 1
H0
2
набл
1 , n 1
H1
2
2

25.

Задача №3
00,1 S 00,2
Проверить гипотезы: 0,05
N=25,
X~N(m, σ),
1) H 0 :
2
2
2
0
H1 :
2
2
0
2
0
Решение:
1. Вычисляем набл. значение стат. критерия
n 1 s
2
2
0
2

26.

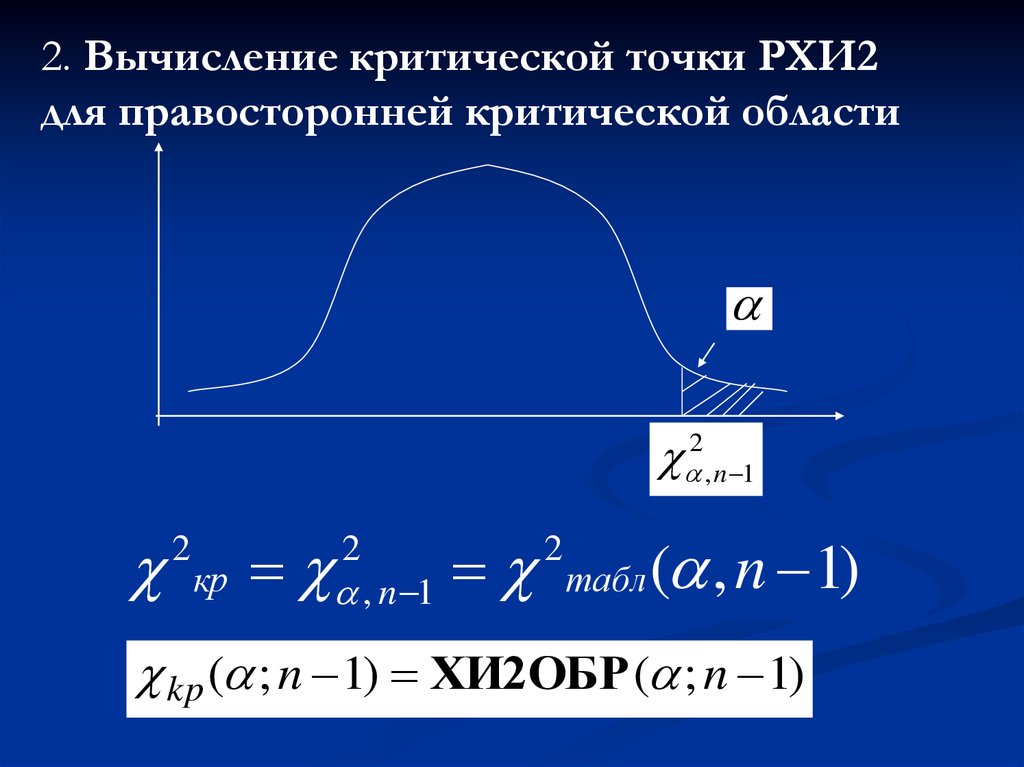
2. Вычисление критической точки РХИ2
для правосторонней критической области
2 , n 1
2
кр
, n 1
2
2
табл
( , n 1)
kp ( ; n 1) ХИ2ОБР ( ; n 1)

27.

3. Принятие решения
2
набл
, n 1
2
набл
, n 1 H1
2
2
H0

28.

Проверка гипотезы о равенстве мат. ожиданий
двух нормальных СВ (известные дисперсии)
1)
2)
3)
X ~ N mx , x , Y ~ N m y , y
H 0 : M X M Y
U
набл
x y
x
2
n
y
2
k
~ N 0,1

29.

Проверка гипотезы о равенстве мат. ожиданий
двух нормальных СВ (известные дисперсии)
4)
1
H1 : M X M Y
u / 2 НОРМСТОБР (1 / 2)
| U набл | u / 2
| U набл | u / 2
H0
H1

30.

Проверка гипотезы о равенстве мат. ожиданий
двух нормальных СВ (известные дисперсии)
2
H1 : M X M Y
5)
u
1
НОРМСТОБР(1 )
U набл u1
H0
U набл u1
H1

31.

Проверка гипотезы о равенстве мат. ожиданий
двух нормальных СВ (известные дисперсии)
5)
3
H1 : M X M Y
u НОРМСТОБР ( )
U набл u
H0
U набл u
H1

32.

Задача №4
n=30, k=40 x 130 2 60 y 125 2 80
y
x
0,05
Проверить гипотезу:
1) H 0 : mx m y , H1 1 : mx my
Решение:
1. Вычисляем набл. значение стат. критерия
U
x y
2
x
n
2
y
k

33.

2. Вычисление критической точки СНЗР
для двусторонней критической области
2
2
U kp
uкр
U
U kp
1
u / 2 Ф u / 2
2
U kp НОРМСТОБР (1 -
2
)

34.

3. Принятие решения
| U набл | uкр
| U набл | uкр
H0
1
H1

35.

Проверка гипотезы о равенстве мат.
ожиданий двух нормальных СВ
(дисперсии неизвестны)
1)
2)
X ~ N mx , x , Y ~ N m y , y
H 0 : M X M Y
3)
T
x y
n 1
2
Sx
k 1
2
Sy
nk n k 2
n k

36.

Проверка гипотезы о равенстве мат.
ожиданий двух нормальных СВ
(дисперсии неизвестны)
4) H1 : M X M Y
1
t / 2, n k 2 СТЬЮДРАСПО БР ( ; n k 2)
| Tнабл | t / 2, n k 2
H0
| Tнабл | t / 2, n k 2
H1

37.

5)
Проверка гипотезы о равенстве мат.
ожиданий двух нормальных СВ
(дисперсии неизвестны)
2
H1 : M X M Y
t , n k 2 СТЬЮДРАСПО БР 2 , n k 2
Tнабл t , n k 2
H0
Tнабл t , n k 2 H1

38.

Проверка гипотезы о равенстве мат.
ожиданий двух нормальных СВ
(дисперсии неизвестны)
6)
3
H1 : M X M Y
t 1 , n k 2 СТЬЮДРАСПО БР 2 , n k 2
Tнабл t 1 , n k 2
H0
Tнабл t 1 , n k 2
H1

39.

Задача №5
n=10, k=16 x 30 S 2 1 y 28 S 2 2
x
y
0,05
Решение:
1. Проводим правостороннюю роверку
H 0 : mx m y ,
H1 : mx m y
2. Вычисляем набл. значение стат. критерия
T набл
x y
n 1
2
Sx
k 1
2
Sy
nk n k 2
n k

40.

3. Вычисление критической точки РС
для правосторонней критической области
t kp
t
tкр tтабл (2 , n 1) табл. для двухсторон ней КО
tкр tтабл ( , n 1) табл. для односторонней КО
t кр СТЬЮДРАСПО БР(2 , n 1)

41.

4. Принятие решения
Tнабл t , n k 2
H0
Tнабл t , n k 2 H1

42.

Проверка гипотезы о равенстве дисперсий
двух нормальных СВ (дисп. неизв.)
1) X ~ N mx , , Y ~ N my ,
2
x
2) H 0 :
2
x
Fнабл
3)
(1)
1
H
2
y
x1 , x2 ,..., xn
2
sx
2
sy
:
2
x
2
y
s s
2
x
y1 , y2 ,..., yk
2
y
Fтабл / 2; n 1; k 1
2
y
FРРАСПОБ / 2; n 1; k 1
Fнабл Fтабл / 2; n 1; k 1
Fнабл Fтабл / 2; n 1; k 1
H0
H1

43.

Проверка гипотезы о равенстве
дисперсий двух нормальных СВ
4)
( 2)
1
H
:
2
x
2
y
Fтабл ; n 1; k 1 FРРАСПОБ ( ; n 1; k 1)
Fнабл Fтабл ; n 1; k 1
H0
Fнабл Fтабл ; n 1; k 1 H1

44.

Задача №6
n=9, k=16
S 34,02
2
x
Проверить гипотезы:
1) H 0 :
2
x
S 12,15
2
y
0,01
H1 :
2
x
2
y
2
y
Решение:
1. Вычисляем набл. значение стат. критерия
S
Fнабл
S
2
x
2
y

45.

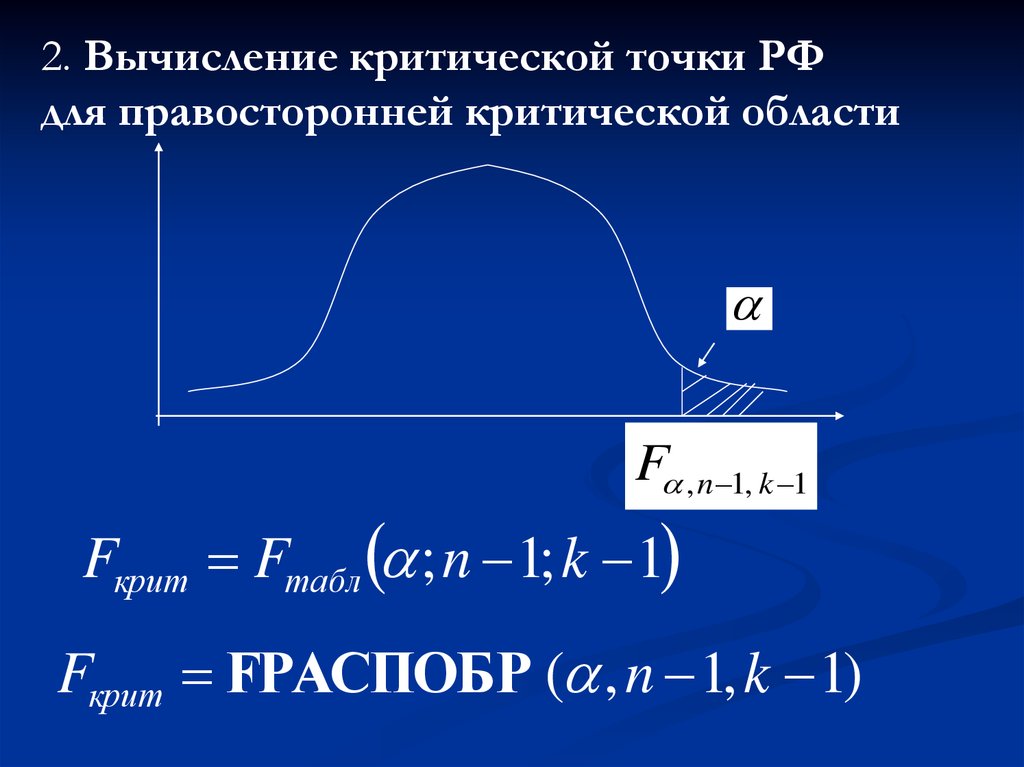
2. Вычисление критической точки РФ
для правосторонней критической области
F , n 1, k 1
Fкрит Fтабл ; n 1; k 1
Fкрит FРАСПОБР ( , n 1, k 1)

46.

3. Принятие решения
Fнабл Fтабл ; n 1; k 1
H0
Fнабл Fтабл ; n 1; k 1 H1