Radar ambiguity function

1. Properties of the MIMO Radar Ambiguity Function

Chun-Yang Chen and P. P. Vaidyanathan
California Institute of Technology
Electrical Engineering/DSP Lab
ICASSP 2008

2. Outline

Review of the background
– Radar ambiguity function and its properties
– MIMO radar
– MIMO radar ambiguity function
Properties of the MIMO ambiguity function
–
–
–
–
Signal component
Energy
Symmetry
Linear frequency modulation (LFM)
Conclusion
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
2

3. Review: Ambiguity function and MIMO radar

3

4. Radar Ambiguity Function

u(t)
u(t-t)ej2pnt
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
t: delay
n: Doppler
4

5. Radar Ambiguity Function

u(t)
Matched filter
output
u(t-t)ej2pnt
t: delay
n: Doppler
(u (t t )e j 2pnt )(u (t t ' )e j 2pn 't )* dt
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
5

6. Radar Ambiguity Function

u(t)
Matched filter
output
u(t-t)ej2pnt
t: delay
n: Doppler
(u (t t )e j 2pnt )(u (t t ' )e j 2pn 't )* dt
u (t )u * (t (t t ' ))e j 2p (n n ')t dt
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
6

7. Radar Ambiguity Function

u(t)
Matched filter
output
u(t-t)ej2pnt
t: delay
n: Doppler
(u (t t )e j 2pnt )(u (t t ' )e j 2pn 't )* dt
u (t )u * (t (t t ' ))e j 2p (n n ')t dt
Radar ambiguity
function
(t ,n ) u (t )u * (t t )e j 2pnt dt
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
7

8. Radar Ambiguity Function

u(t)
Matched filter
output
u(t-t)ej2pnt
t: delay
n: Doppler
(u (t t )e j 2pnt )(u (t t ' )e j 2pn 't )* dt
u (t )u * (t (t t ' ))e j 2p (n n ')t dt
Radar ambiguity
function
(t ,n ) u (t )u * (t t )e j 2pnt dt
Ambiguity function characterizes the Doppler and range
resolution.
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
8

9. Radar Ambiguity Function

u (t )
Multiple targets
(tk,nk)
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
9

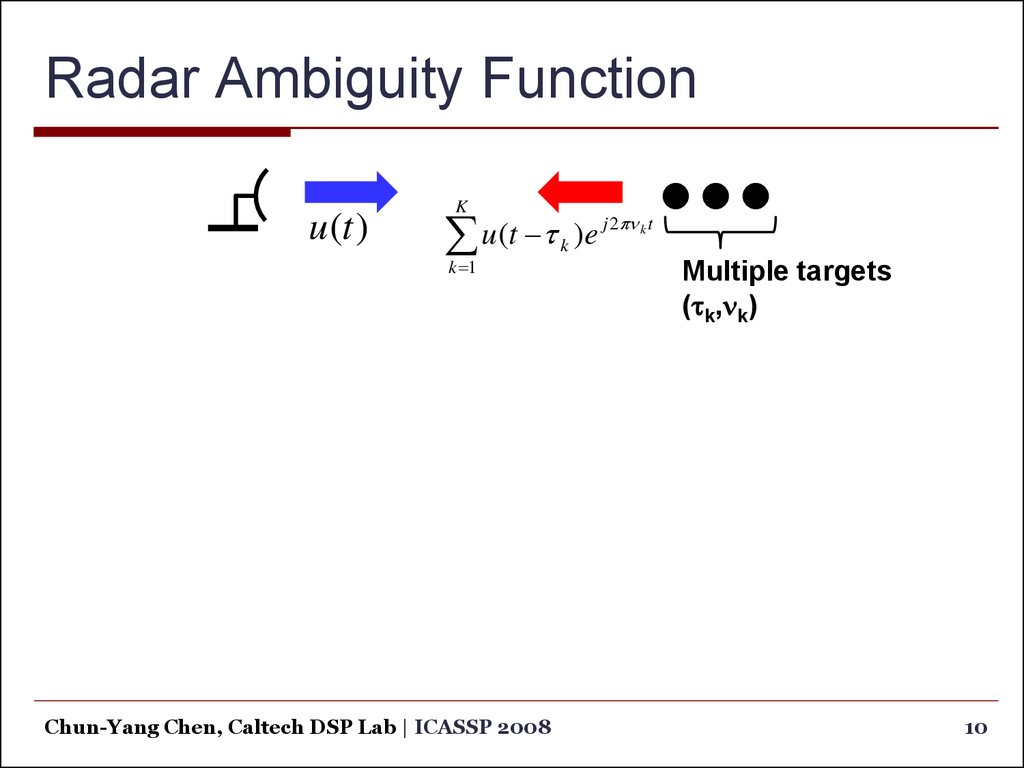
10. Radar Ambiguity Function

u (t )
K
j 2pn k t
u
(
t
t
)
e
k
k 1
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
Multiple targets
(tk,nk)
10

11. Radar Ambiguity Function

u (t )
K
j 2pn k t
u
(
t
t
)
e
k
k 1
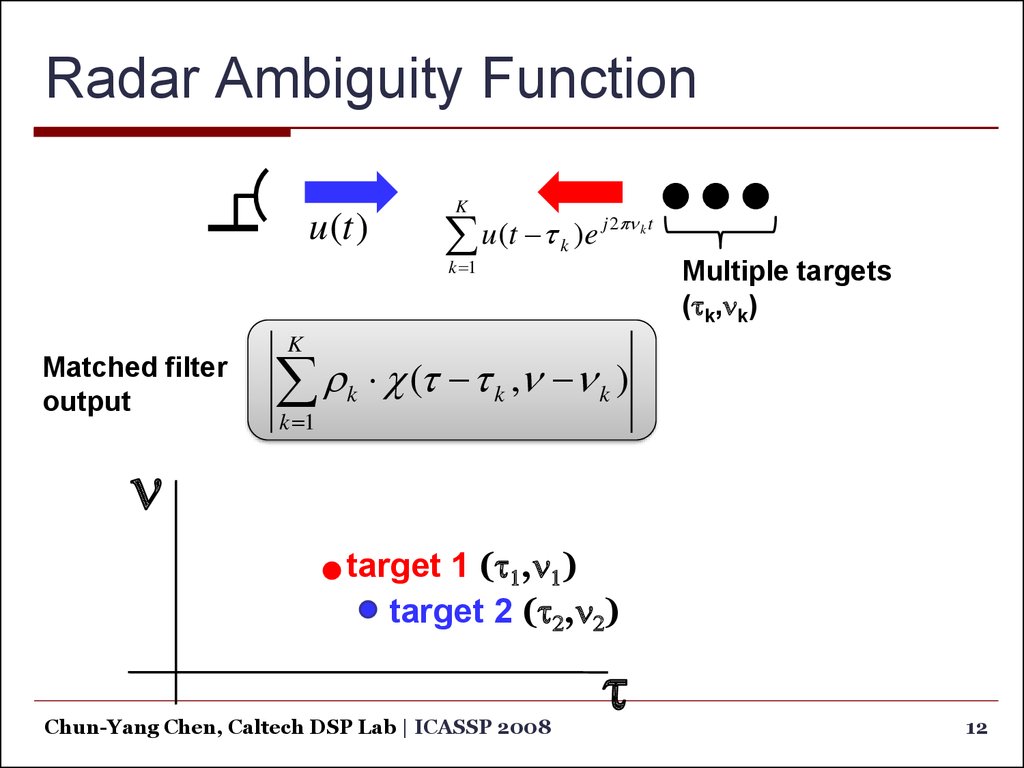
Matched filter
output
K
k 1
k
Multiple targets
(tk,nk)
(t t k ,n n k )
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
11

12. Radar Ambiguity Function

u (t )
K
j 2pn k t
u
(
t
t
)
e
k
k 1
Matched filter
output
K
k 1
k
Multiple targets
(tk,nk)
(t t k ,n n k )
n
target 1 (t1,n1)
target 2 (t2,n2)
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
t
12

13. Radar Ambiguity Function

u (t )
K
j 2pn k t
u
(
t
t
)
e
k
k 1
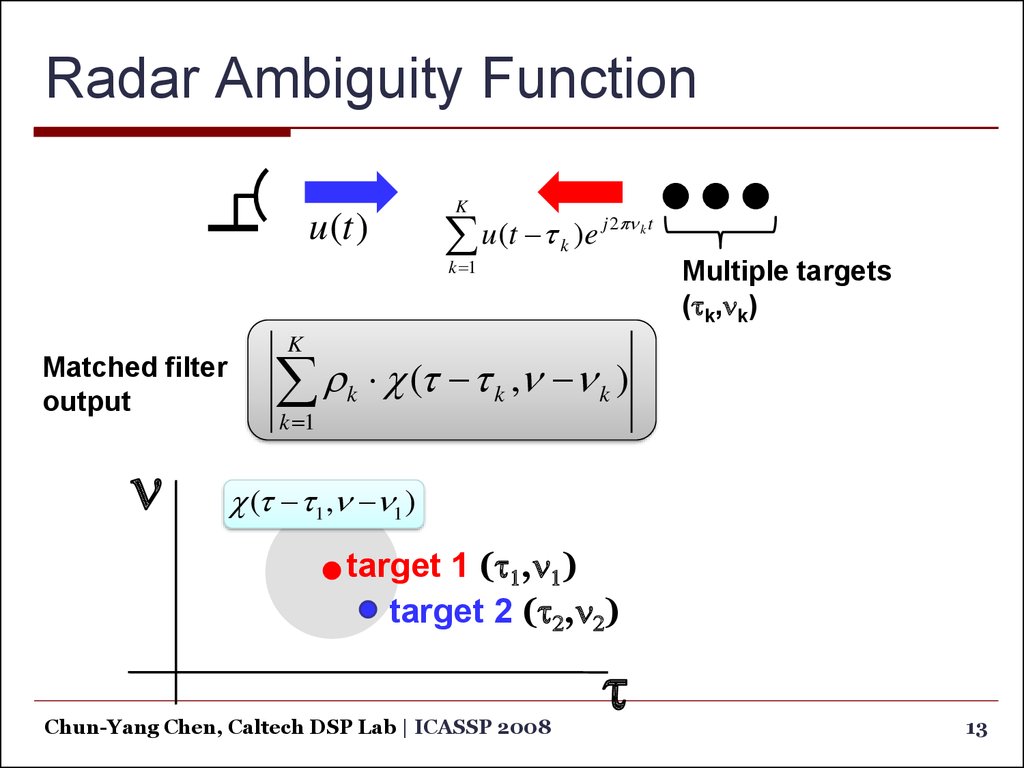
Matched filter
output
n
K
k 1
k
Multiple targets
(tk,nk)
(t t k ,n n k )
(t t1,n n1 )
target 1 (t1,n1)
target 2 (t2,n2)
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
t
13

14. Radar Ambiguity Function

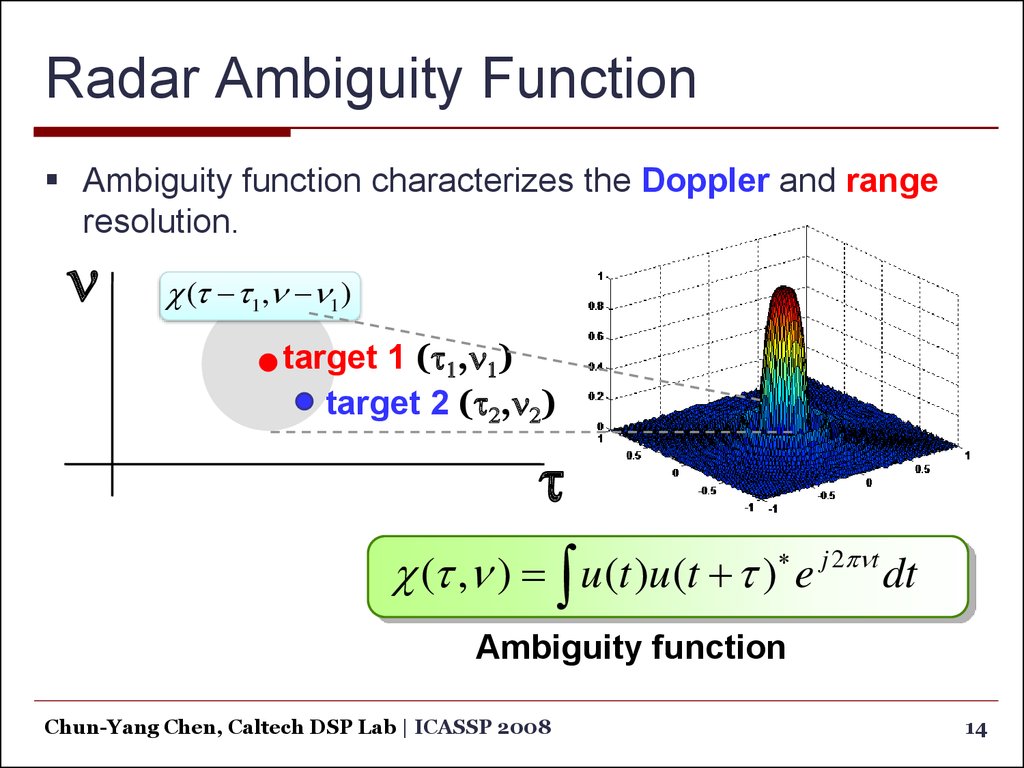
Ambiguity function characterizes the Doppler and range
resolution.
n
(t t1,n n1 )
target 1 (t1,n1)
target 2 (t2,n2)
t
(t ,n ) u (t )u (t t ) e
j 2pnt
dt
Ambiguity function
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
14

15. Radar Ambiguity Function

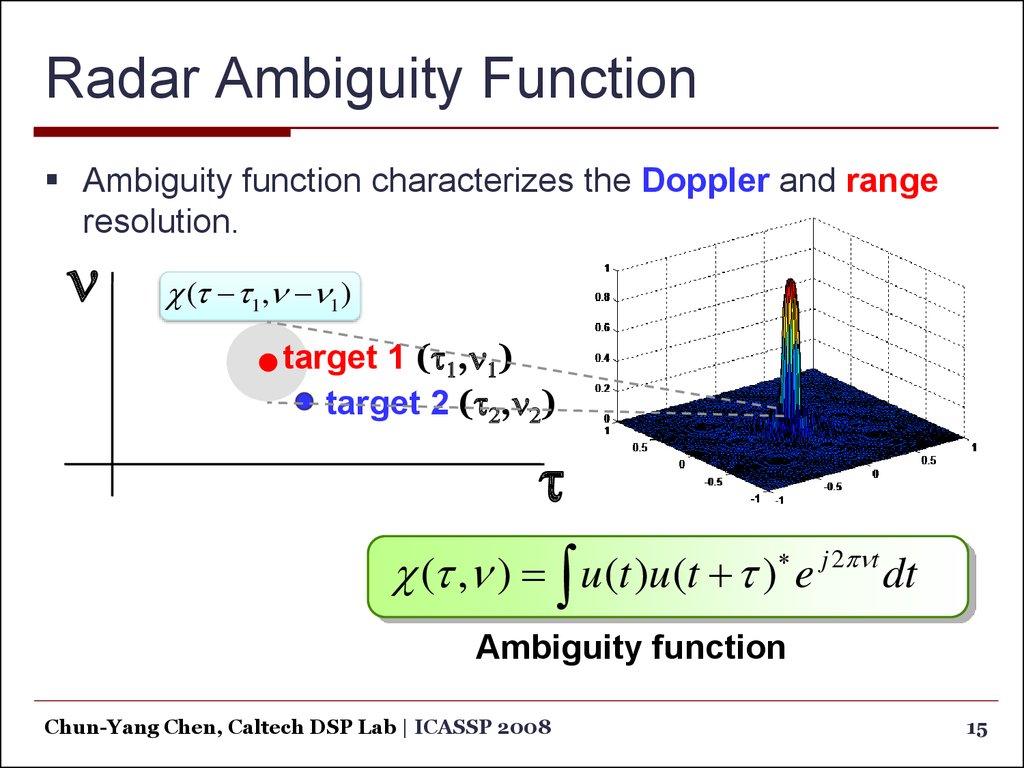
Ambiguity function characterizes the Doppler and range
resolution.
n
(t t1,n n1 )
target 1 (t1,n1)
target 2 (t2,n2)
t
(t ,n ) u (t )u (t t ) e
j 2pnt
dt
Ambiguity function
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
15

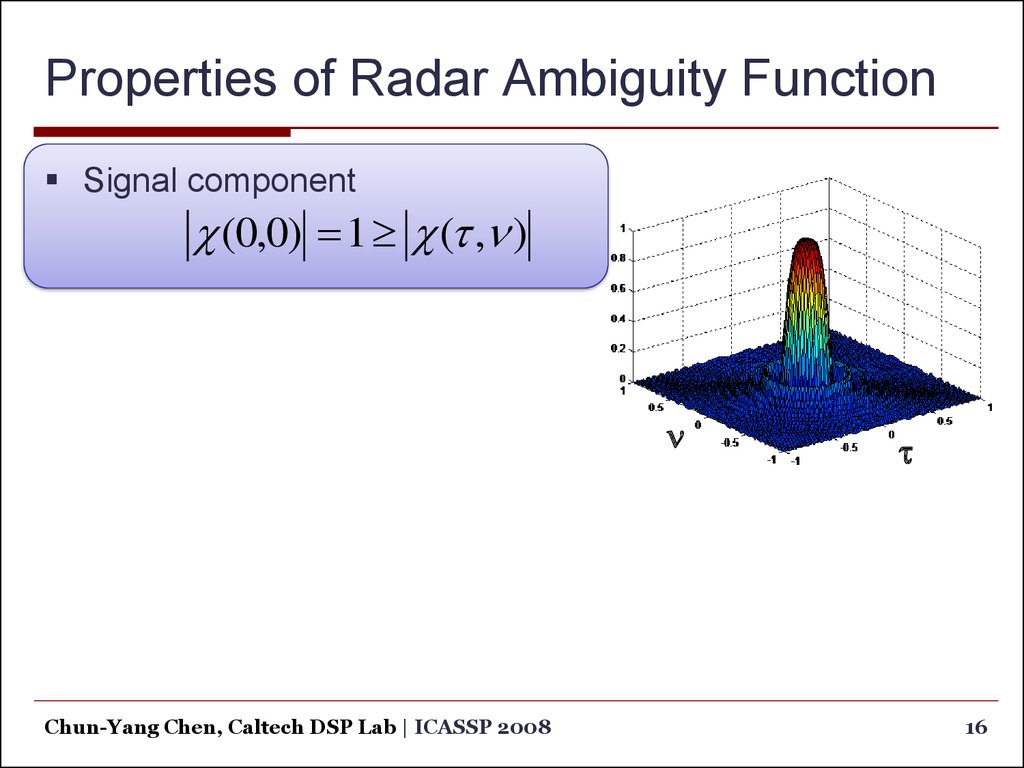
16. Properties of Radar Ambiguity Function

Signal component
(0,0) 1 (t ,n )
n
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
t
16

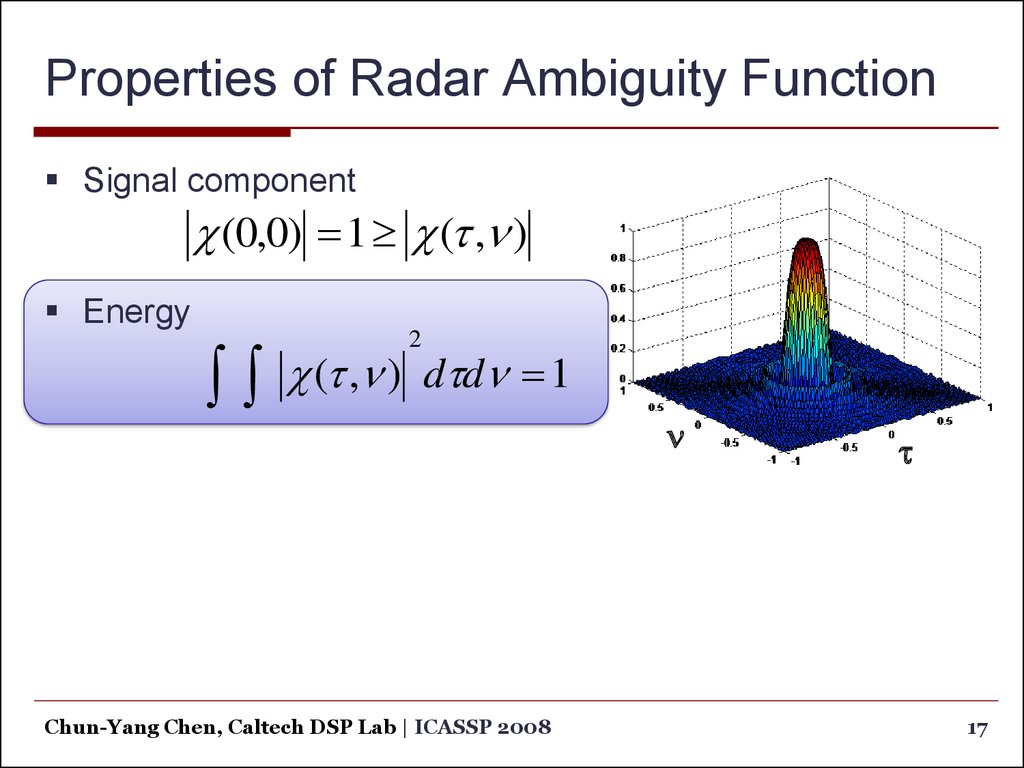
17. Properties of Radar Ambiguity Function

Signal component
(0,0) 1 (t ,n )
Energy
2
(t ,n ) dtdn 1
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
n
t
17

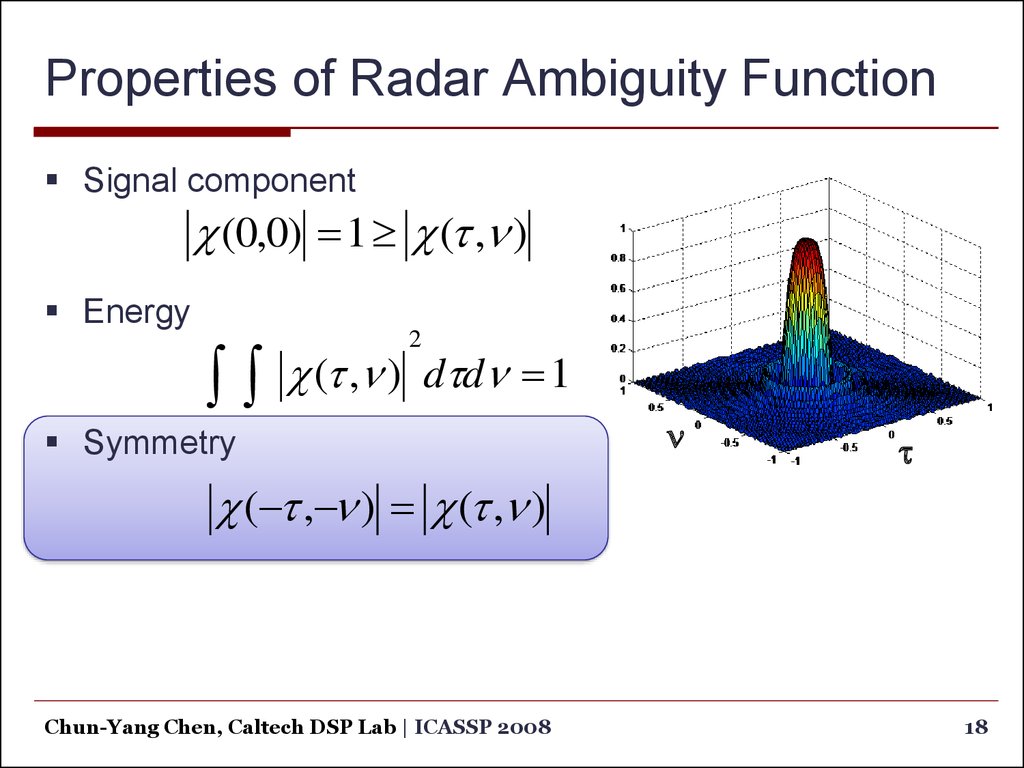
18. Properties of Radar Ambiguity Function

Signal component
(0,0) 1 (t ,n )
Energy
2
(t ,n ) dtdn 1
Symmetry
n
t
( t , n ) (t ,n )
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
18

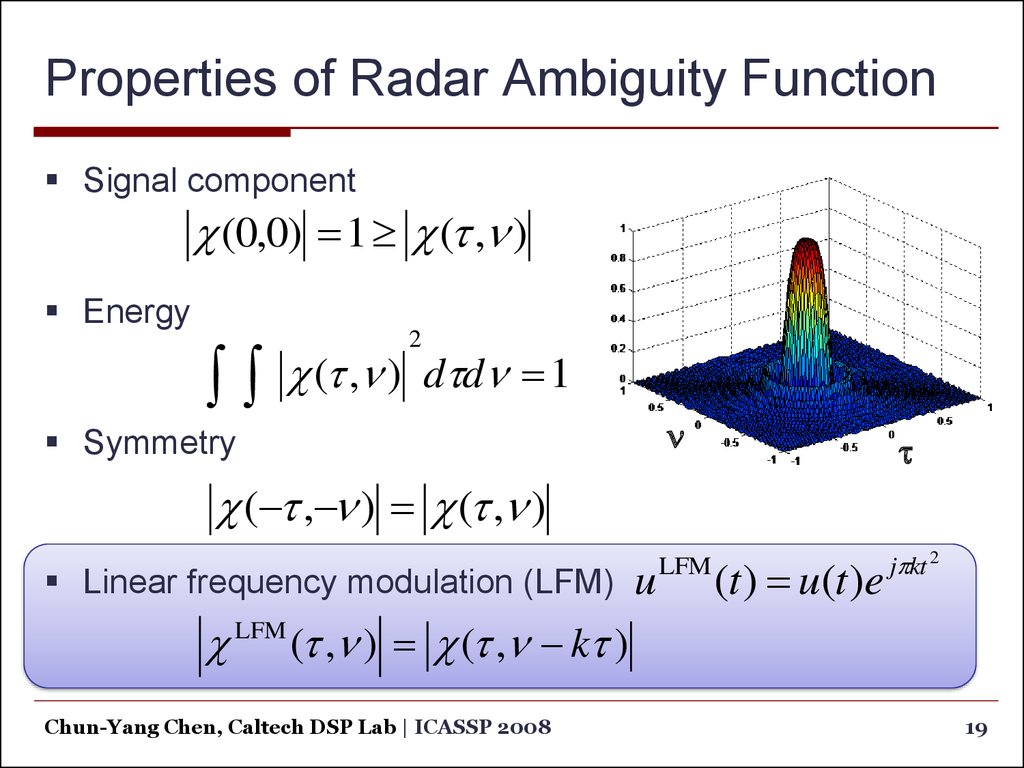
19. Properties of Radar Ambiguity Function

Signal component
(0,0) 1 (t ,n )
Energy
2
(t ,n ) dtdn 1
n
Symmetry
t
( t , n ) (t ,n )
Linear frequency modulation (LFM)
u
LFM
(t ) u(t )e
jpkt 2
LFM (t ,n ) (t ,n kt )
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
19

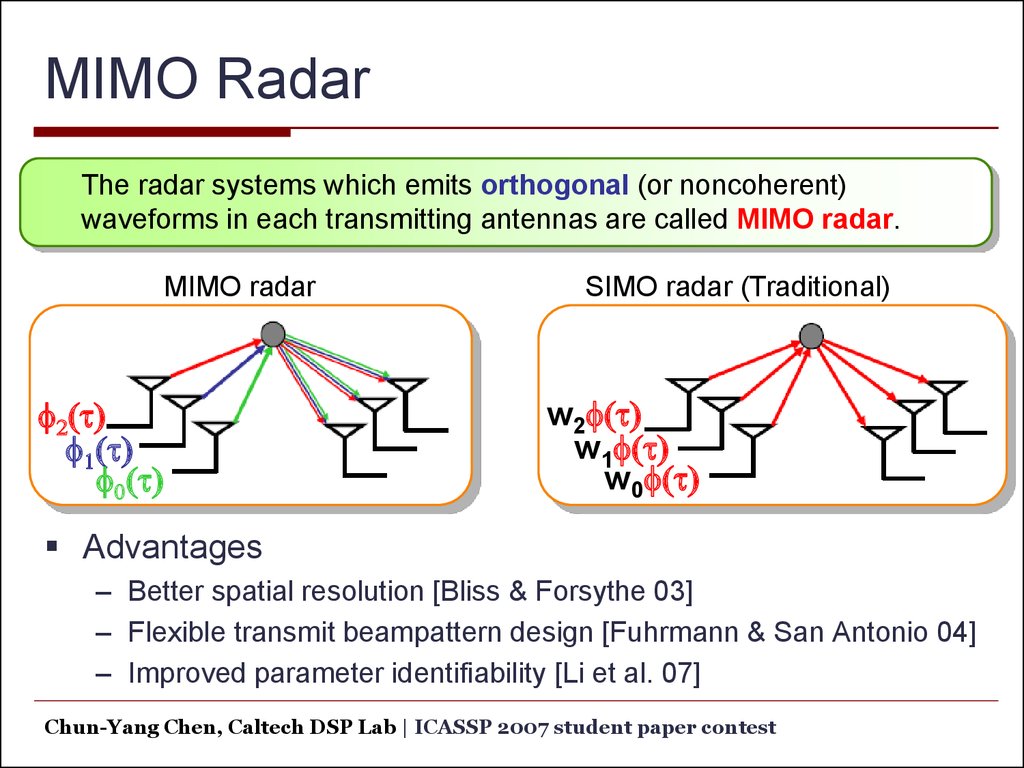
20. MIMO Radar

The radar systems which emits orthogonal (or noncoherent)
waveforms in each transmitting antennas are called MIMO radar.
MIMO radar
f2(t)
f1(t)
f0(t)
SIMO radar (Traditional)
w2f(t)
w1f(t)
w0f(t)
Advantages
– Better spatial resolution [Bliss & Forsythe 03]
– Flexible transmit beampattern design [Fuhrmann & San Antonio 04]
– Improved parameter identifiability [Li et al. 07]
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2007 student paper contest

21. Ambiguity Function in MIMO Radar

(t,n,f) t:delay
n:Doppler
f: Spatial freq.
TX
dT
u0(t) u1(t)
…
uM-1(t)
Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007
21

22. Ambiguity Function in MIMO Radar

(t,n,f)
TX
dT
u0(t) u1(t)
t:delay
n:Doppler
f: Spatial freq.
RX
…
uM-1(t)
(t,n,f)
…
dR
MF
…
MF
…
Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007
MF
…
22

23. Ambiguity Function in MIMO Radar

(t,n,f)
TX
dT
u0(t) u1(t)
t:delay
n:Doppler
f: Spatial freq.
RX
…
uM-1(t)
(t,n,f)
…
dR
MF
…
MF
…
y
(t ,n , f )
Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007
MF
…
(t )
23

24. Ambiguity Function in MIMO Radar

(t,n,f)
TX
RX
…
dT
u0(t) u1(t)
uM-1(t)
Matched filter output
(y
(t ',n ', f ')
t:delay
n:Doppler
f: Spatial freq.
(t,n,f)
…
dR
MF
…
MF
…
y
(t ,n , f )
MF
…
(t )
(t ) ) y (t ,n , f ) (t )dt
H
Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007
24

25. Ambiguity Function in MIMO Radar

Matched filter output
(y
(t ',n ', f ')
(t ) ) y (t ,n , f ) (t )dt
H
( u
N 1
M 1 M 1
n 0
m 0 m ' 0
j 2p ( f f ') n
e
t:delay
n:Doppler
f: Spatial freq.
um(t): m-th waveform
xm: m-th antenna location
n: receiving antenna index
)
*
j 2p (n v ') t
j 2p ( fm f 'm ')
(
t
t
)
u
(
t
t
'
)
e
dt
e
m
m
Receiver beamforming
Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007
25

26. Ambiguity Function in MIMO Radar

Matched filter output
(y
(t ',n ', f ')
(t ) ) y (t ,n , f ) (t )dt
H
( u
N 1
M 1 M 1
n 0
m 0 m ' 0
j 2p ( f f ') n
e
t:delay
n:Doppler
f: Spatial freq.
um(t): m-th waveform
xm: m-th antenna location
n: receiving antenna index
)
*
j 2p (n v ') t
j 2p ( fm f 'm ')
(
t
t
)
u
(
t
t
'
)
e
dt
e
m
m
Receiver beamforming
m,m ' (t ,n ) um (t )um* ' (t t )e j 2pn t dt
Cross ambiguity function
Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007
26

27. Ambiguity Function in MIMO Radar

Matched filter output
(y
(t ',n ', f ')
(t ) ) y (t ,n , f ) (t )dt
H
( u
N 1
M 1 M 1
n 0
m 0 m ' 0
j 2p ( f f ') n
e
t:delay
n:Doppler
f: Spatial freq.
um(t): m-th waveform
xm: m-th antenna location
n: receiving antenna index
)
*
j 2p (n v ') t
j 2p ( fm f 'm ')
(
t
t
)
u
(
t
t
'
)
e
dt
e
m
m
Receiver beamforming
m,m ' (t ,n ) um (t )um* ' (t t )e j 2pn t dt
[San Antonio et al. 07]
M 1 M 1
(t ,n , f , f ' ) m,m ' (t ,n )e j 2p ( fm f 'm ')
m 0 m ' 0
MIMO ambiguity function
Chun-Yang Chen, Caltech DSP Lab | Asilomar Conference 2007
27

28. Properties of the MIMO ambiguity function

28

29. Properties of the signal component

Ambiguity function:
Signal component:
(t ,n , f , f ' )
(0,0, f , f )
(0,0, f , f ' )
f ' f
f'
(0,0, f , f )
f
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
29

30. Properties of the signal component

Ambiguity function:
Signal component:
(0,0, f , f ' )
(t ,n , f , f ' )
(0,0, f , f )
For orthogonal waveforms,
um (t )um* ' (t )dt mm'
f ' f
f'
(0,0, f , f )
f
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
30

31. Properties of the signal component

Ambiguity function:
Signal component:
(0,0, f , f ' )
(t ,n , f , f ' )
(0,0, f , f )
For orthogonal waveforms,
f ' f
f'
(0,0, f , f )
um (t )um* ' (t )dt mm'
(0,0, f , f ) M , f
If the waveforms are orthogonal,
the signal component will be a
constant for all angle.
f
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
31

32. Properties of the signal component

Ambiguity function:
Signal component:
(t ,n , f , f ' )
(0,0, f , f )
For general waveforms,
For orthogonal waveforms,
um (t ) dt 1
2
um (t )um* ' (t )dt mm'
(0,0, f , f ) M , f
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
32

33. Properties of the signal component

Ambiguity function:
Signal component:
(t ,n , f , f ' )
(0,0, f , f )
For general waveforms,
If
dT
For orthogonal waveforms,
um (t ) dt 1
2
is integer,
um (t )um* ' (t )dt mm'
(0,0, f , f ) M , f
(0,0, f , f ) df M , f
The integration of the signal
component is a constant if dT is
a multiple of the wavelength.
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
dT is the spacing
between the
transmitting antennas
33

34. Properties of the signal component

Ambiguity function:
Signal component:
(t ,n , f , f ' )
(0,0, f , f )
For general waveforms,
If
For orthogonal waveforms,
um (t ) dt 1
dT
dT is the spacing
between the
transmitting antennas
2
is integer,
um (t )um* ' (t )dt mm'
(0,0, f , f ) M , f
(0,0, f , f ) df M , f
For the general case,
2dT / M (0,0, f , f ) df 2dT / M
2d T /
2d T /
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
In general, the
integration of the
signal component is
confined.
34

35. Energy of the cross ambiguity function

Cross ambiguity function:
mm' (t ,n ) um (t )um* ' (t t )e j 2pnt dt
Energy of the cross ambiguity function:
mm' (t ,n ) dt dn
2
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
35

36. Energy of the cross ambiguity function

Cross ambiguity function:
mm' (t ,n ) um (t )um* ' (t t )e j 2pnt dt
Energy of the cross ambiguity function:
mm' (t ,n ) dt dn
2
u
m
(t )u (t t )e
*
m'
j 2pnt
2
dt dndt
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
36

37. Energy of the cross ambiguity function

Cross ambiguity function:
mm' (t ,n ) um (t )um* ' (t t )e j 2pnt dt
Energy of the cross ambiguity function:
mm' (t ,n ) dt dn
2
u
m
(t )u (t t )e
*
m'
j 2pnt
2
dt dndt
um (t )u (t t ) dtdt
*
m'
2
Parserval
relation
( u (t ) dt ) 1
2
2
m
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
37

38. Energy of the cross ambiguity function

Cross ambiguity function:
mm' (t ,n ) um (t )um* ' (t t )e j 2pnt dt
Energy of the cross ambiguity function:
mm' (t ,n ) dt dn 1
2
The energy of the cross
ambiguity function is a
constant.
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
38

39. Energy of the MIMO ambiguity function

MIMO ambiguity function:
M 1 M 1
(t ,n , f , f ' ) mm' (t ,n )e j 4pd
T
/ ( fm f 'm ')
m 0 m ' 0
Energy of the ambiguity function
(t ,n , f , f ' )
2
dtdndfdf '
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
39

40. Energy of the MIMO ambiguity function

MIMO ambiguity function:
M 1 M 1
(t ,n , f , f ' ) mm' (t ,n )e j 4pd
T
/ ( fm f 'm ')
m 0 m ' 0
Energy of the ambiguity function
(t ,n , f , f ' )
M 1 M 1
m 0 m ' 0
2
dtdndfdf '
2
j 4pdT / ( fm f 'm ')
(
t
,
n
)
e
dfdf ' dtdn
mm'
dT is the spacing
between the
transmitting antennas
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
40

41. Energy of the MIMO ambiguity function

MIMO ambiguity function:
M 1 M 1
(t ,n , f , f ' ) mm' (t ,n )e j 4pd
T
/ ( fm f 'm ')
m 0 m ' 0
Energy of the ambiguity function
(t ,n , f , f ' )
M 1 M 1
m 0 m ' 0
M 1 M 1
2
dT is the spacing
between the
transmitting antennas
dtdndfdf '
2
j 4pdT / ( fm f 'm ')
(
t
,
n
)
e
dfdf ' dtdn
mm'
mm' (t ,n ) dtdn
2
m 0 m ' 0
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
If dT is a multiple of
the wavelength, we
can apply Parserval
relation for 2D DFT.
41

42. Energy of the MIMO ambiguity function

MIMO ambiguity function:
M 1 M 1
(t ,n , f , f ' ) mm' (t ,n )e j 4pd
T
/ ( fm f 'm ')
m 0 m ' 0
Energy of the ambiguity function
(t ,n , f , f ' )
M 1 M 1
m 0 m ' 0
M 1 M 1
2
dtdndfdf '
2
j 4pdT / ( fm f 'm ')
(
t
,
n
)
e
dfdf ' dtdn
mm'
mm' (t ,n ) dtdn
2
m 0 m ' 0
M 1 M 1
1 M
m 0 m ' 0
2
Cross ambiguity
function has
constant energy
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
dT is the spacing
between the
transmitting antennas
42

43. Energy of the MIMO ambiguity function

If dT is a multiple of the wavelength,
2
(
t
,
n
,
f
,
f
'
)
d
t
d
n
dfdf
'
M
2
dT is the spacing
between the
transmitting antennas
If dT is a multiple of the
wavelength, the energy of
the MIMO ambiguity function
is a constant.
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
43

44. Energy of the MIMO ambiguity function

If dT is a multiple of the wavelength,
2
(
t
,
n
,
f
,
f
'
)
d
t
d
n
dfdf
'
M
2
dT is the spacing
between the
transmitting antennas
Recall that the signal component satisfies,
(0,0, f , f ) df
M , f
– Because energy and the signal component are both constants,
we can only spread the energy to minimize the peak.
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
44

45. Energy of the MIMO ambiguity function

If dT is a multiple of the wavelength,
2
(
t
,
n
,
f
,
f
'
)
d
t
d
n
dfdf
'
M
2
dT is the spacing
between the
transmitting antennas
In general, the energy satisfies,
2dT /
2
2dT / M 2
2
(
t
,
n
,
f
,
f
'
)
d
t
d
n
dfdf
'
M
(2dT / )2
(2dT / )2
2
2
In general, the energy of the
MIMO ambiguity function is
confined in a certain range.
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
45

46. Energy of the MIMO ambiguity function

If dT is a multiple of the wavelength,
2
(
t
,
n
,
f
,
f
'
)
d
t
d
n
dfdf
'
M
2
dT is the spacing
between the
transmitting antennas
In general, the energy satisfies,
2dT /
2
2dT / M 2
2
(
t
,
n
,
f
,
f
'
)
d
t
d
n
dfdf
'
M
(2dT / )2
(2dT / )2
2
2
In general, the signal component satisfies,
2dT / M (0,0, f , f ) df 2dT / M
2d T /
2d T /
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
46

47. Symmetry properties

Symmetry of the cross ambiguity function
mm' ( t , n ) m'm (t ,n )
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
47

48. Symmetry properties

Symmetry of the cross ambiguity function
mm' ( t , n ) m'm (t ,n )
Symmetry of the MIMO ambiguity function
( t , n , f , f ' ) (t ,n , f ' , f )
It suffices to show only half of
the ambiguity function (t>0).
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
48

49. Linear frequency modulation (LFM)

Linear frequency modulation
u
LFM
m
(t ) um (t )e
jpkt 2
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
49

50. Linear frequency modulation (LFM)

Linear frequency modulation
u
LFM
m
(t ) um (t )e
jpkt 2
Cross ambiguity function
LFM
mm'
(t ,n ) mm' (t ,n kt )
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
50

51. Linear frequency modulation (LFM)

Linear frequency modulation
u
LFM
m
(t ) um (t )e
jpkt 2
Cross ambiguity function
LFM
mm'
(t ,n ) mm' (t ,n kt )
MIMO ambiguity function
LFM
Shear off
(t ,n , f , f ' ) (t ,n kt , f , f ' )
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
51

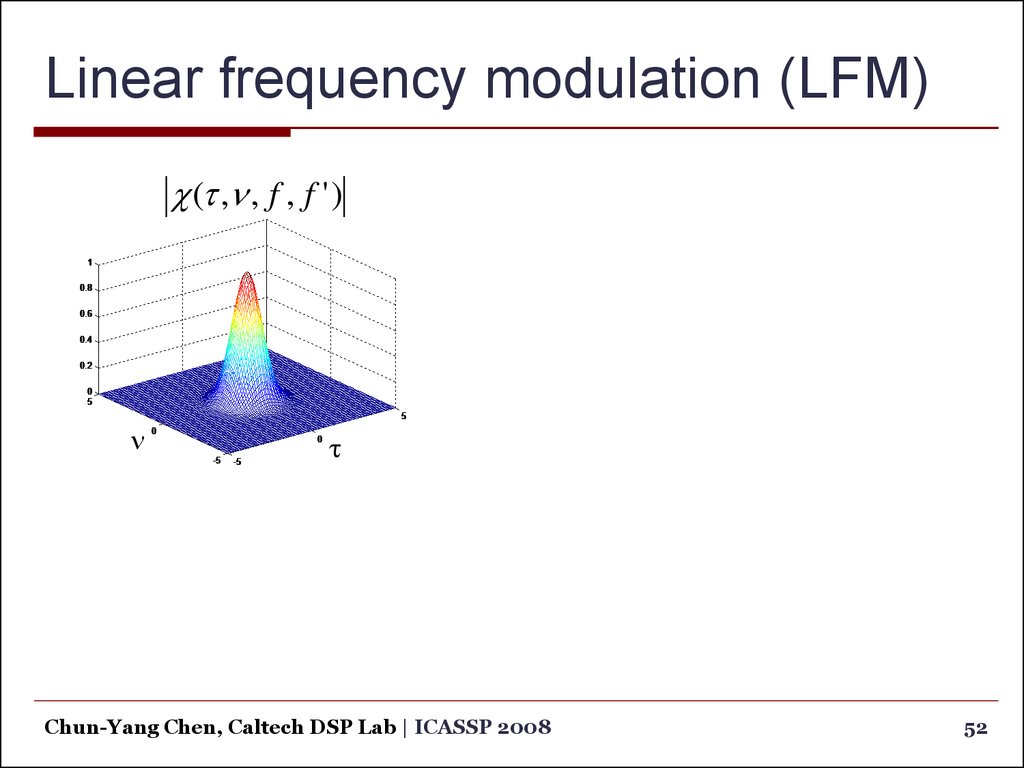
52. Linear frequency modulation (LFM)

(t ,n , f , f ' )
n
t
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
52

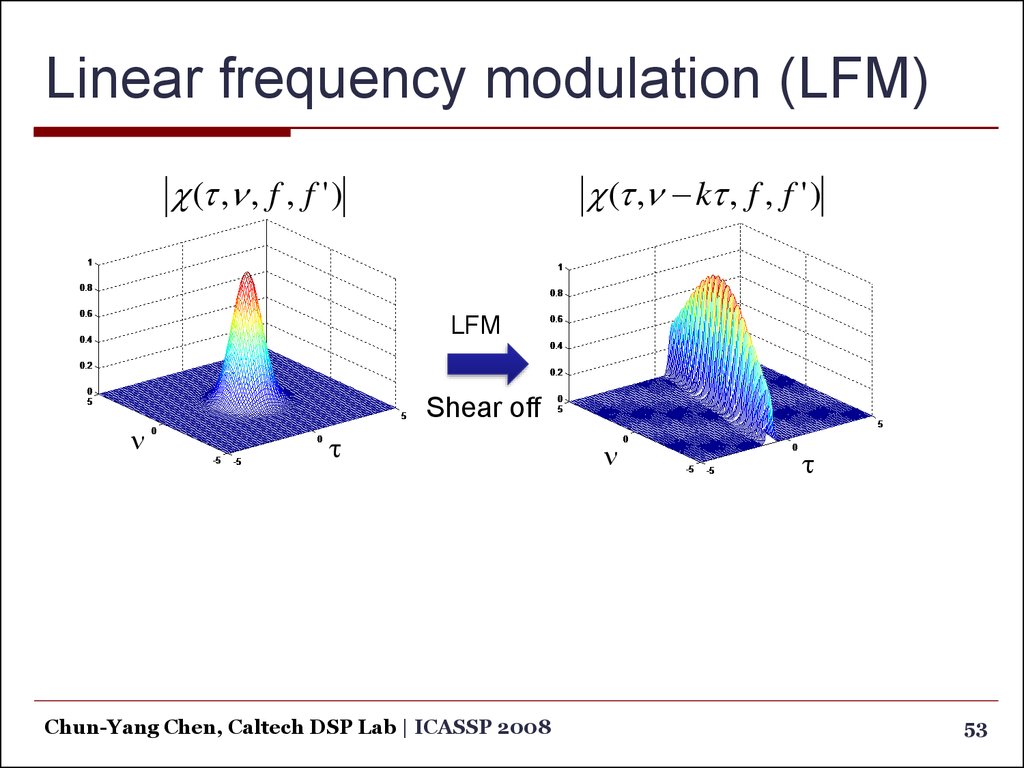
53. Linear frequency modulation (LFM)

(t ,n kt , f , f ' )
(t ,n , f , f ' )
LFM
n
Shear off
t
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
n
t
53

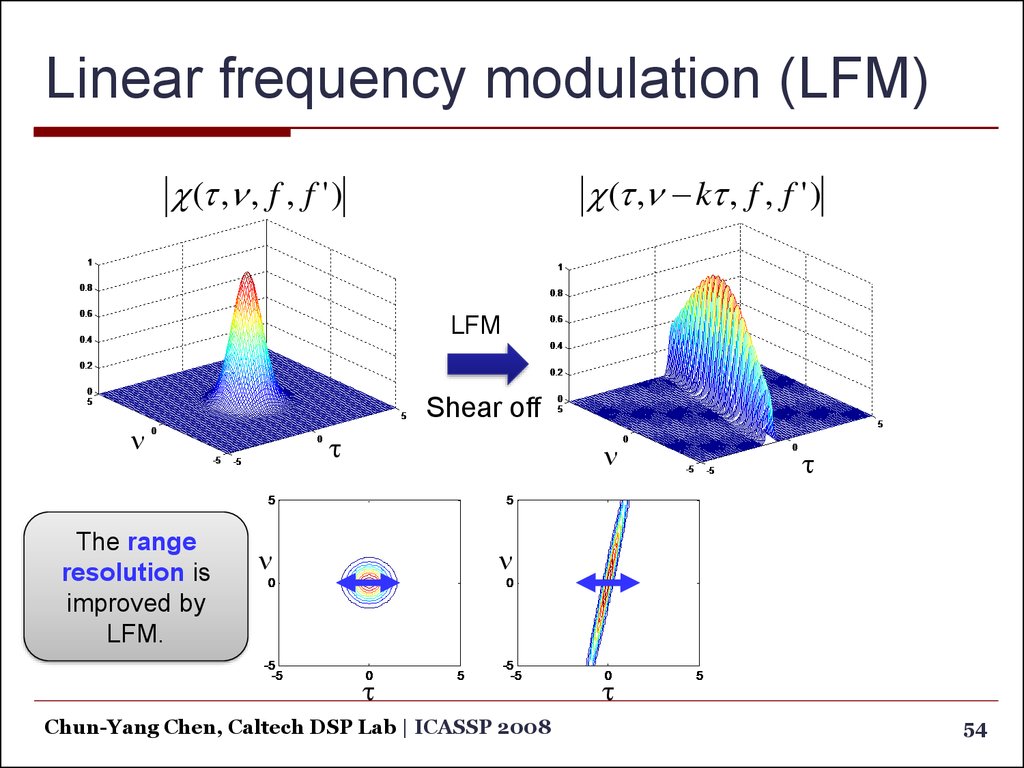
54. Linear frequency modulation (LFM)

(t ,n kt , f , f ' )
(t ,n , f , f ' )
LFM
Shear off
n
The range
resolution is
improved by
LFM.
t
n
n
t
n
t
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
t
54

55. Conclusion

Properties of the MIMO ambiguity function
– Signal component
2dT / M (0,0, f , f ) df 2dT / M
2d T /
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
2d T /
55

56. Conclusion

Properties of the MIMO ambiguity function
– Signal component
2dT / M (0,0, f , f ) df 2dT / M
2d T /
– Energy
2d T /
2
2dT / M 2
2dT / M 2
(
t
,
n
,
f
,
f
'
)
d
t
d
n
dfdf
'
(2dT / )2
(2dT / )2
2
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
2
56

57. Conclusion

Properties of the MIMO ambiguity function
– Signal component
2dT / M (0,0, f , f ) df 2dT / M
2d T /
– Energy
– Symmetry
2d T /
2
2dT / M 2
2dT / M 2
(
t
,
n
,
f
,
f
'
)
d
t
d
n
dfdf
'
(2dT / )2
(2dT / )2
2
2
( t , n , f , f ' ) (t ,n , f ' , f )
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
57

58. Conclusion

Properties of the MIMO ambiguity function
– Signal component
2dT / M (0,0, f , f ) df 2dT / M
2d T /
– Energy
– Symmetry
– LFM
2d T /
2
2dT / M 2
2dT / M 2
(
t
,
n
,
f
,
f
'
)
d
t
d
n
dfdf
'
(2dT / )2
(2dT / )2
2
2
( t , n , f , f ' ) (t ,n , f ' , f )
LFM (t ,n , f , f ' ) (t ,n kt , f , f ' )
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
58

59. Thank You!

Q&A
Any questions?
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
59

60. Properties of the signal component

If the waveforms are
orthogonal, the
signal component
will be a constant
for all angle.
For orthogonal waveforms,
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
um (t )um* ' (t )dt mm'
(0,0, f , f ) M , f
60

61. Properties of the signal component

For general waveforms,
If
dT
um (t ) dt 1
2
is integer,
(0,0, f , f ) df M , f
The integration of
the signal
component is a
constant if dT is a
multiple of the
wavelength.
dT is the spacing
between the
transmitting antennas
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
61

62. Properties of the signal component

In general, the
integration of the signal
component is confined
in a certain range.
For the general case,
2dT / M (0,0, f , f ) df 2dT / M
2d T /
2d T /
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
dT is the spacing
between the
transmitting antennas
62

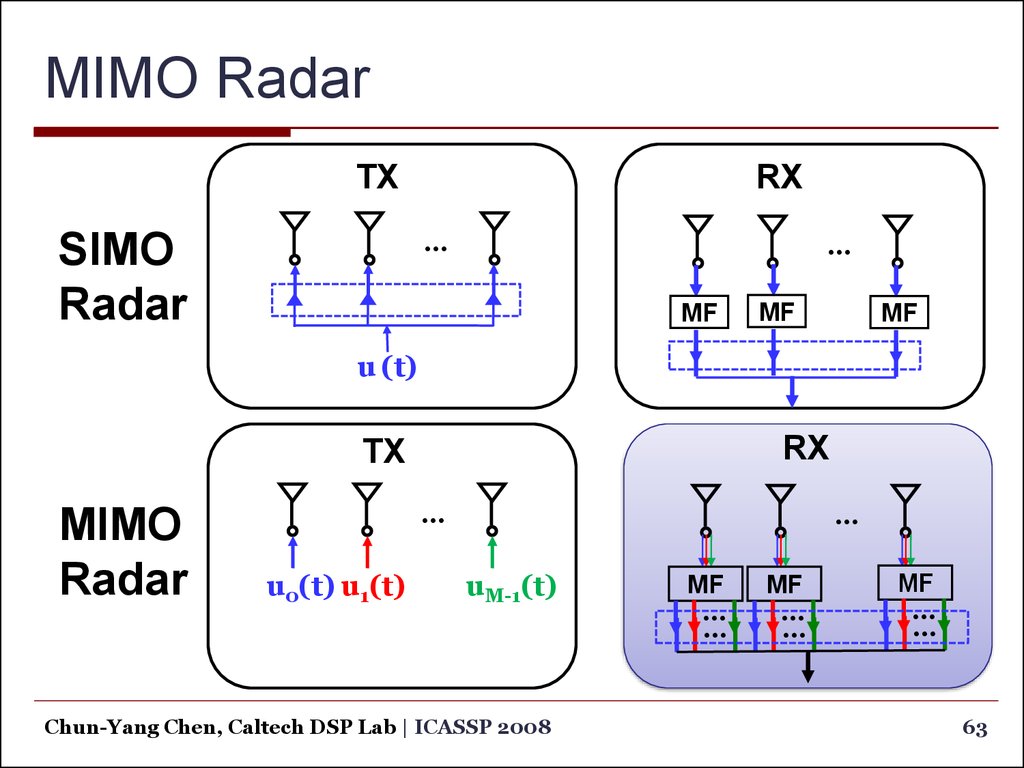
63. MIMO Radar

TX
RX
…
SIMO
Radar
…
MF
MF
MF
u (t)
RX
TX
MIMO
Radar
…
u0(t) u1(t)
…
uM-1(t)
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
MF
…
…
MF
…
…
MF
…
…
63

64. MIMO Radar

Advantages
– Better spatial resolution [Bliss & Forsythe 03]
– Flexible transmit beampattern design [Fuhrmann & San Antonio 04]
– Improved parameter identifiability [Li et al. 07]
RX
TX
MIMO
Radar
…
u0(t) u1(t)
…
uM-1(t)
Chun-Yang Chen, Caltech DSP Lab | ICASSP 2008
MF
…
…
MF
…
…
MF
…
…
64