Разложение функций в степенные ряды. Приближенное вычисление значений функции. Интегрирование функций. (Семинар 28)

1. Семинар 28

Разложение функций в
степенные ряды. Приближенное
вычисление значений функции.
Интегрирование функций

2.

Предположим, что функция f(x) бесконечное число раз дифференцируема
окрестности некоторой точки x0 . Допустим, что ее можно представить в
виде суммы степенного ряда, сходящегося в каком-то интервале,
содержащем точку x0 .
f ( x) a0 a1 ( x x0 ) a 2 ( x x0 ) 2 ... a n ( x x0 ) n ...(*) , где a0 , a1 ,..., an - пока
неопределенные коэффициенты. Покажем, как пользуясь свойствами
степенных рядов можно найти эти коэффициенты по известным значениям
функции f(x) и ее производных в точке x 0 .
Положим в (*) x x0 . Получаем f ( x0 ) a0 . Продифференцируем степенной
n 1
ряд f ' ( x) a1 2a 2 ( x x0 ) ... na n ( x x0 ) ... и снова положим x x0.
Получим f ' ( x0 ) a1 . Последующее дифференцирование дает
f ' ( x) 2a 2 ... n(n 1)a n ( x x0 ) n 2 ... При x x0 ; f " ( x0 ) 2a2 , то есть
a2
f " ( x0 )
2!
После n-кратного дифференцирования получает f ( n ) ( x) n!a n ... Все
( x x0 ) . При получим f ( n ) ( x0 ) n!a n ,
остальные элементы
содержат
множитель
f ( n ) ( x0 )
то есть a n
n!

3.

Таким образом, находятся последовательно все коэффициенты разложения
(*). Подставляя найденные выражения в равенство (*) получим ряд
f " ( x0 )
f ( n ) ( x0 )
2
f ( x) f ( x0 ) f ' ( x0 )( x x0
( x x0 ) ...
( x x0 ) n ...(**) . Такой ряд
2!
n!
называется рядом Тейлора функции f(x).
Остаточный член ряда Тейлора. Формула Тейлора.
Пусть f(x) – функция, относительно которой хотим выяснить, допускает она
разложение в ряд Тейлора в окрестности некоторой точки х 0 или нет.
Запишем ее в следующем виде:
f ( n ) ( x0 )
'
x x0 n Rn x (*) , где
f ( x) Tn ( x) Rn (n) f ( x0 ) f ( x0 )( x x0 ) ...
n!
Rn (x) - остаточный член ряда Тейлора.
Рассмотрим теорему относительно структуры Rn (x) , которая в дальнейшем
позволит устанавливать, стремится ли Rn (x) к нулю при неограниченном
возрастании n или нет, то есть можно ли представить функцию в виде ряда
Тейлора или нет.

4.

Теорема
Если функция f(x) во всех точках некоторого интервала, содержащего точку x 0 ,
имеет (n+1) производную f ( n 1) ( x) , то остаточный член R (x) для любой точки
n
n 1
(
x
x
)
этого интервала имеет вид R ( x) f ( n 1)
, где заключено
0
n
(n 1)!
между x и x 0 ( ( x0 , x))
В соответствии с такой записью Rn (x) формула (*) имеет вид
f ( n ) ( x0 )
f ( n 1) (
x x0
f ( x) Tn ( x) Rn (n) f ( x0 ) f ( x0 )( x x0 ) ...
( x x0 ) n 1 (**)
n!
(n 1)!
'
В таком виде эту формулу называют формулой Тейлора n-го порядка для
функции f(x) в точке .
Приближенное вычисление значений функции
Допустим, что нам известны значения самой функции f(x) и ее
последовательных производных в некоторой точке x 0 и f(x) в окрестности этой
точки разлагается в ряд Тейлора. Тогда точное значение функции f(x) в любой
точке этой окрестности может быть вычислено по ряду Тейлора
приближенное ее значение по частичной сумме этого ряда.

5.

Возникающую при этом ошибку можно оценивать либо опираясь на теорему
об оценке остаточного члена, либо непосредственно оценивая остаток ряда.
Если, например, получающийся числовой ряд знакочередующийся, то это
делается при помощи теоремы Лейбница; в случае знакоположительного
ряда стараются подобрать другой ряд (обычно геометрическую прогрессию),
элементы которого больше элементов остатка и, сумму которых мы можем
найти.
На практике оценка остатка ряда оказывается более удобной, так как оценка
остаточного члена предполагает знание производной нужного нам порядка во
всем рассматриваемом интервале. Часто можно получить разложение
функций в ряды, вообще не отыскивая производных, а комбинируя известные
нам ряды.
Интегрирование функций
x
Допустим, что нужно найти интеграл F ( x) f ( x)dx причем известно
a
разложение функции f(x) в ряд Тейлора, а пределы интегрирования лежат
внутри интервала сходимости ряда.

6.

Тогда можно интегрировать ряд поэлементно. В результате получаем ряд
Тейлора для
функции F(x), имеющей тот же радиус сходимости, что и ряд для
x
f(x). Если f ( x)dx выражается через элементарную функцию F(x), то тем
a
x
самым находим ее разложение в ряд Тейлора. Если же f ( x)dx в
a
элементарных функциях не выражается, то найденный ряд может служить
выражением неэлементарной функции F(x) через самые простые
элементарные функции – степенные, но уже бесконечным выражением.
Замечание Зная оценку остаточного члена ряда для f(x) можно на основании
теоремы об оценке интеграла можно оценить и остаточный член ряда для
интеграла F(x).
Примеры с решениями:
x2
1. Разложить в степенной ряд e 2
x x
xn
2
x
Решение. В разложении e 1 ... ...( x ) заменяя x x
1!
2!
n!
x2 x4
x 2n
...( x )
получаем e 1 ...
1! 2!
n!
x2

7.

2. Разложить lnx по степеням x-1
n
x2
n 1 x
...( 1 x 1) заменяя x на x-1
Решение. В разложении ln( 1 x) x ... ( 1)
2
n
n
( x 1) 2
n 1 ( x 1)
... ( 1)
...(0 x 2)
получаем ln x ( x 1)
2
n
1
3. Разложить 1/x в ряд по степеням x-2.
1
2
Решение. Воспользуемся равенством
x 1 ( x 2) / 2
Правую часть равенства можно рассматривать как сумму бесконечно
убывающей геометрической прогрессии с первым элементом a=1/2 и
знаменателем q=-(x-2)/2.
2
1
1
1
x
2
1
x
2
1
x
2
1 1
1
2
Отсюда получаем
... ( x 2) ( x 2) _ ....
x
2 2
2 2 2 2
2
2 4
Так как |(x-2)/2|<1, то 0<x<4.
1
4. Вычислить 5 с точностью до 0,00001
e 1
1
1
1
Решение. Имеем 5 e 1 / 5 1 2 3 ... Воспользуемся
1!5
e
приближенным равенством
1
5
e
2!5
3!5
e 1 / 5 1
1
1
1
1
2 3 4
1!5 2!5 3!5 4!5
8

8.

Мы взяли 5 слагаемых, так как знакопеременный ряд удовлетворяет
условиям признака Лейбница, а поэтому допускаемая погрешность по
абсолютной величине должна быть меньше первого из отброшенных
элементов ряда.
1
Первый из отброшенных элементов равен 5 0,00001
5!5
Вычислим алгебраическую сумму элементов
1,000000-0,200000+0,020000-0,001333+0,000067=0,818734.
Итак
1
5
e
0,81873
5. Вычислить ln1,04 с точностью до 0,0001
Решение. Воспользуемся разложением ln(1+x) в ряд:
0,04 2 0,04 3 0,04 4
ln 1,04 ln( 1 0,04) 0,04
... 0,04 0,0008 0,000021 0,00000064 ...
2
3
4
откуда ln 1,04 0,0392

9.

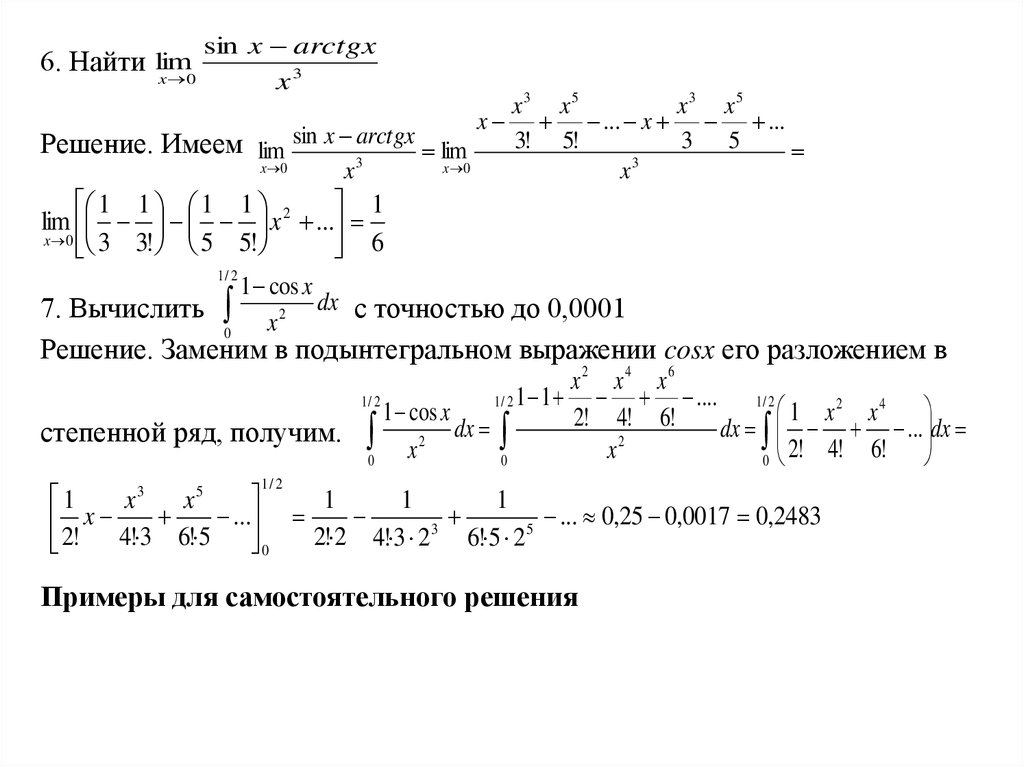
sin x arctgx
x3
6. Найти lim
x 0
x3 x5
x3 x5
x ... x ...
sin
x
arctgx
3! 5!
3 5
Решение. Имеем lim
lim
3
3
x 0
x 0
x
x
1 1 1 1
1
lim x 2 ...
x 0
3 3! 5 5!
6
1/ 2
1 cos x
7. Вычислить x 2 dx с точностью до 0,0001
0
Решение. Заменим в подынтегральном выражении cosx его разложением в
x2 x4 x6
.... 1 / 2
1/ 2
1/ 2 1 1
1 x2 x4
1 cos x
2
!
4
!
6
!
dx
dx ... dx
степенной ряд, получим.
2
2
2! 4! 6!
x
x
0
0
0
1/ 2
1
x
x
1
1
1
x
...
... 0,25 0,0017 0,2483
3
5
2
!
4
!
3
6
!
5
2
!
2
4
!
3
2
6
!
5
2
0
3
5
Примеры для самостоятельного решения

10.

Примеры для самостоятельного решения
1.Разложить в ряд Тейлора функцию в окрестности указанной точки:
1
1) y
2) y x 3 ln x, x0 1
3) y 1 x 3 , x0 0
, x0 2
x 5
2. С помощью разложения функции в степенной ряд вычислить значение
функции с точностью до 0,001:
1
1
1) 0.98 2) 11 2000 3) arcsin 4) 4
3
e
3. Используя разложение в ряд подынтегральной функции, вычислить
значение интеграла с точностью до 0,001:
0 ,8
0,5
1
2)
ln(
1
x
1) cos x dx 2)
dx 3) (1 x 4 ) 1 dx
0
0
x
0