Вычисление значений многочлена. Вычисление функций с помощью степенных рядов. Многочленные приближения

1. Лекция 2

1. Вычисление значений многочлена.
Схема Горнера
2. Вычисление функций с помощью
степенных рядов
3. Многочленные приближения
4. Вычисление функций методом
итераций

2.

Вычисление значений различных математических функций иногда
представляет собой самостоятельную задачу, а иногда необходимо при
решении других задач. Функции, даже элементарные, не могут быть
вычислены с помощью операций языка программирования, и поэтому
вычисляются с помощью программ.
Некоторые
элементарные
функции
(тригонометрические,
логарифмические, гиперболические и ряд других) могут быть
вычислены с помощью программ, входящих в состав систем
программирования. Например, для вычисления функций при
программировании на языке Visual Basic могут быть использованы
многочисленные процедуры (методы) класса System.Math. Для
использования этих функций в программе на Visual Basic необходимо в
начале файла с программой поместить код Imports System.Math.
Еще большие возможности по вычислению функций дают
математические пакеты прикладных программ (ППП), например,
знакомые вам MathCad и MatLab. Но на практике может возникнуть
необходимость вычисления функции, отсутствующей даже в ППП, а,
следовательно, необходимость разработки собственной программы с
использованием известных методов решения задачи. В любом случае
необходимо знать методы вычисления различных функций и оценки
вносимых ими погрешностей, чтобы грамотно использовать готовые
программы, а при необходимости решить задачу самостоятельно.

3. Вычисление значений многочлена. Постановка задачи

Пусть дан многочлен (полином) n-й
степени:
Pn(x) = a0xn + a1xn-1 + … + an-1x + an
с действительными коэффициентами
ai (i = 0, 1,…n)
и пусть требуется найти значение этого
многочлена при x = u:
Pn(u) = a0un + a1un-1 + … + an-1u + an

4. Вычисление значений многочлена. Схема Горнера

Вычисление эффективнее всего выполнять, используя лишь операции сложения
и умножения. Пусть, например, n = 7. Тогда
P7(u) = a0u7 + a1u6 + a2u5 + a3u4 + a4u3 + a5u2 + a6u + a7
Представим это выражение в следующем виде:
P7(u) = (((((((a0u +a1)u + a2)u + a3)u + a4)u + a5)u + a6)u + a7)
Тогда вычисление P7(u) требует выполнения следующей последовательности
действий:
b0 = a0
c1 = b0u
b1 = a1 + c1
c2 = b1u
b2 = a2 + c2
c3 = b2u
b3 = a3 + c3
c4 = b3u
b4 = a4 + c4
c5 = b4u
b5 = a5 + c5
c6 = b5u
b6 = a6 + c6
c7 = b6u
b7 = a7 + c7

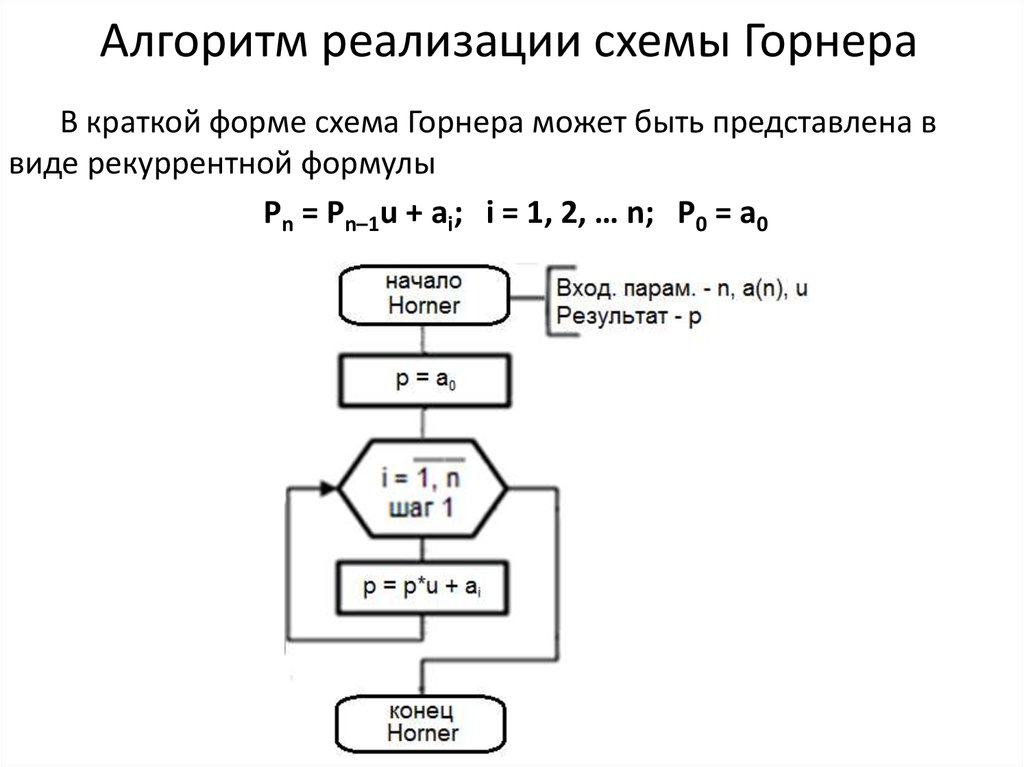
5. Алгоритм реализации схемы Горнера

В краткой форме схема Горнера может быть представлена в
виде рекуррентной формулы
Pn = Pn–1u + ai; i = 1, 2, … n; P0 = a0

6. Разложение функций в ряд Маклорена

Некоторые трансцендентные (т.е. неалгебраические)
функции раскладываются в ряд Маклорена:
f (k) (0) k
f(x)
x
k!
k 0
Представим этот бесконечный ряд в виде суммы
f(x) = Pn(x) + Rn(x),
где
n
(k)
f (0) k
Pn (x)
x
k!
k 0
а Rn(x) – остаточный член.

7. Разложение функций в ряд Маклорена

R n (x) 0, и при
Если ряд Маклорена сходится, то lim
n
достаточно малом Rn(x) значение функции f(x) ≈ Pn(x)
с абсолютной погрешностью Rn(x). Таким образом,
погрешность этого метода вычисления значений
функций определяется величиной Rn(x) и может
регулироваться
путем
выбора
количества
суммируемых членов ряда n.
При вычислении функции путем разложения в ряд
Маклорена надо знать радиус сходимости ряда, т.е.
ограничения на величину x, и оценку величины Rn(x)
для обеспечения
условия |Rn(x)| < ε, где ε –
заданная допустимая абсолютная погрешность.

8. Рекуррентные формулы

Во многих случаях вычисление членов ряда
непосредственно по общей формуле члена ряда
трудоемко и может вызвать дополнительные ошибки
округления. В таких случаях очередной член ряда
вычисляют не по общей, а по рекуррентной формуле –
через предыдущий член ряда. Для получения
рекуррентной
формулы
необходимо
выполнить
следующие операции:
1. Записать формулу для k–го члена ряда ak.
2. Записать формулу для (k-1)-го члена ряда ak-1, заменив
в предыдущей формуле всюду k на k-1.
3. Получить формулу для отношения q = ak/ak-1,
произведя необходимые упрощения и сокращения.
4. Записать в развернутом виде полученную
рекуррентную формулу в виде ak= q ∙ ak-1, значения k,
при которых она работает, и значение первого члена
ряда a0.

9. Разложение в ряд Маклорена некоторых элементарных функций

k
2
3
x
x
x
e x ak 1 x ... ; | x | ; R n (x) | an |
2! 3!
k 0
k 0 k!
n
n
x 2k 1
x 3 x5
sin x ak ( 1)
x ... ; | x | ; R n (x) | an 1 |
(2 k 1)!
3! 5!
k 0
k 0
n
n
k
x2k
x2 x4
cos x ak ( 1)
1 ... ; | x | ; R n (x) | an 1 |
(2 k)!
2! 4!
k 0
k 0
n
n
k
x 2k 1
x 3 x5
arctg x ak ( 1)
x ... ; | x | 1; R n (x) | an 1 |
(2 k 1)
3 5
k 0
k 0
n
n
k

10. Разложение в ряд Маклорена некоторых элементарных функций

1
1 x 2 k 1
(
)
;
k 0 2 k 1 1 x
n
n
ln x a k 2
k 0
0.5 x 1;
R n (x)
1
an
4
x2k
x 2 x4
2
cosh x ak
1 ... ; | x | ; R n (x) an
2! 4!
3
k 0
k 0 (2 k)!
n
n
x 2k 1
x 3 x5
1
sinh x ak
x ... ; | x | ; R n (x) | an |
3! 5!
3
k 0
k 0 (2 k 1)!
n
n

11. Вывод рекуррентной формулы для ряда ex

k
2
3
x
x
x
e x ak 1 x ... ; | x | ; R n (x) | an |
2! 3!
k 0
k 0 k!
n
n
k
x
1. ak
k!
xk-1
2. ak-1
(k- 1)!
ak
xk 1 2 (k - 1)
x
3. q
k -1
ak-1 1 2 (k- 1) k x
k
x
4. ak ak-1 ; k 1, 2, 3, ; a 0 1
k
s k s k 1 ak ; k 1, 2, 3, ; s 0 1

12. Приведение аргумента ex к диапазону|x| < 1

Приведение аргумента ex к диапазону|x| < 1
При больших по абсолютной величине
значениях x данный ряд сходится медленно, и за
счет погрешностей округления результат может
оказаться
не
просто
неточным,
а
бессмысленным. Скорость сходимости ряда
будет большой при |x| < 1. Для приведения x к
этому диапазону его представляют обычно в
виде суммы:
x = E(x) + z, где E(x) – целая часть x, 0<=z<1 –
дробная часть x. Тогда ex = eE(x) ∙ ez, где eE(x)
вычисляется путем возведения в целую степень,
а ez – путем разложения в ряд.

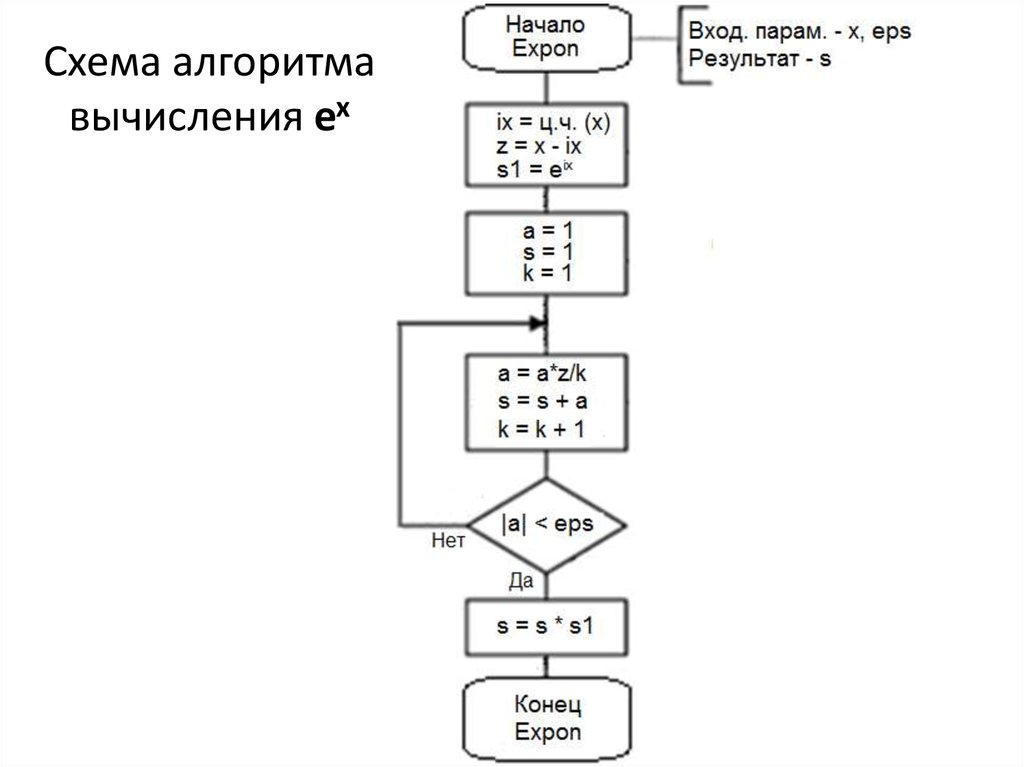
13. Схема алгоритма вычисления ex

14. Рекуррентные формулы для рядов sin(x) и cos(x)

2 k 1
3
5
x
x
x
sin x ak ( 1)k
x ... ; | x | ; R n (x) | an 1 |
(2 k 1)!
3! 5!
k 0
k 0
n
n
2
x
ak ak-1
; k 1, 2, 3, ; a 0 x
2 k(2 k 1)
s k s k 1 ak ; k 1, 2, 3, ; s 0 x
x2k
x2 x4
cos x ak ( 1)
1 ... ; | x | ; R n (x) | an 1 |
(2 k)!
2! 4!
k 0
k 0
n
n
k
2
x
ak ak-1
; k 1, 2, 3, ; a 0 1
(2 k 1)2 k
s k s k 1 ak ; k 1, 2, 3, ; s 0 1

15. Приведение аргумента sin(x) и cos(x) к отрезку [0; π/4]

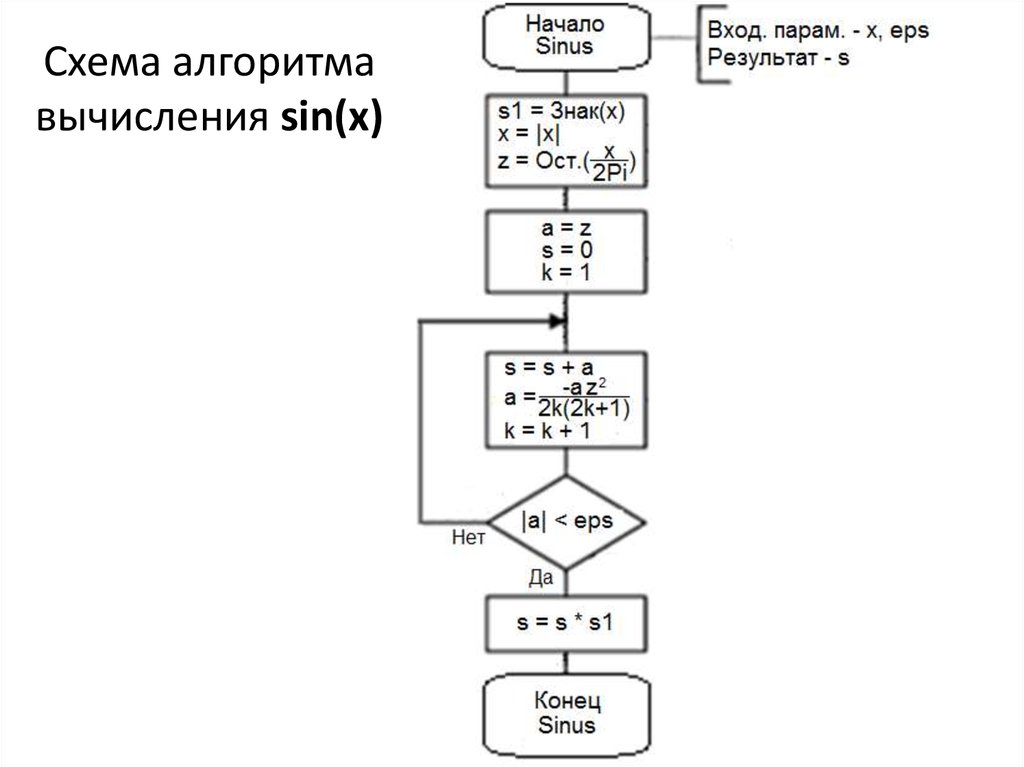
16. Схема алгоритма вычисления sin(x)

17. Рекуррентные формулы и формулы приведения для функции arctg(x)

x 2k 1
x 3 x5
arctg x ak ( 1)
x ... ; | x | 1; R n (x) | an 1 |
(2 k 1)
3 5
k 0
k 0
n
n
k
x (2 k 1)
a k a k-1
; k 1, 2, 3, ; a 0 x
2k 1
2
s k s k 1 a k ; k 1, 2, 3, ; s 0 x
Нечетность: arctg(-x) = -arctg(x)
Приведение к |x|<=1: arctg(x) = π/2 - arctg(1/x)

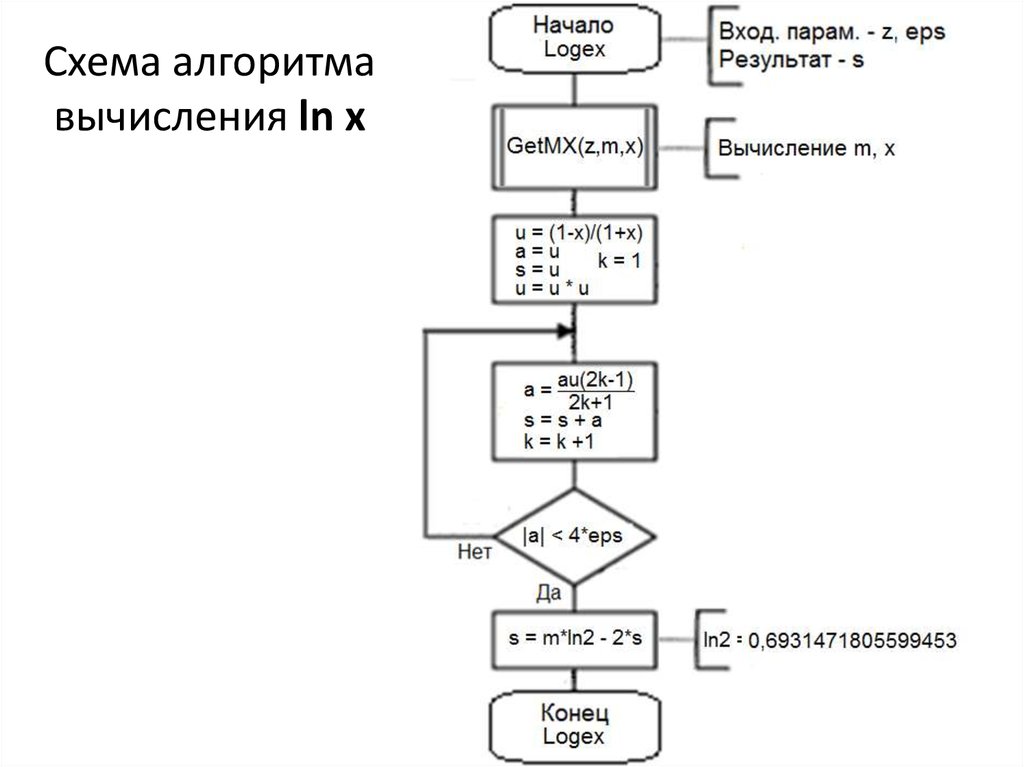
18. Рекуррентные формулы и формулы приведения для функции ln(z)

n
1
1 x 2 k 1
(
)
;
k 0 2 k 1 1 x
n
ln x a k 2
k 0
0.5 x 1;
R n (x)
1
an
4
(1 x)2 (2 k 1)
1 x
a k ak-1
; k 1, 2, 3, ; a 0
2
(1 x) (2 k 1)
1 x
s k s k 1 ak ;
k 1, 2, 3, ; s 0 x
Представим z в виде z = 2m ∙ x, где m – целое
число и 0.5≤x<1. Прологарифмировав это
равенство, получим ln z = m ∙ ln 2 + ln x
ln 2 ≈ 0,6931471805599453

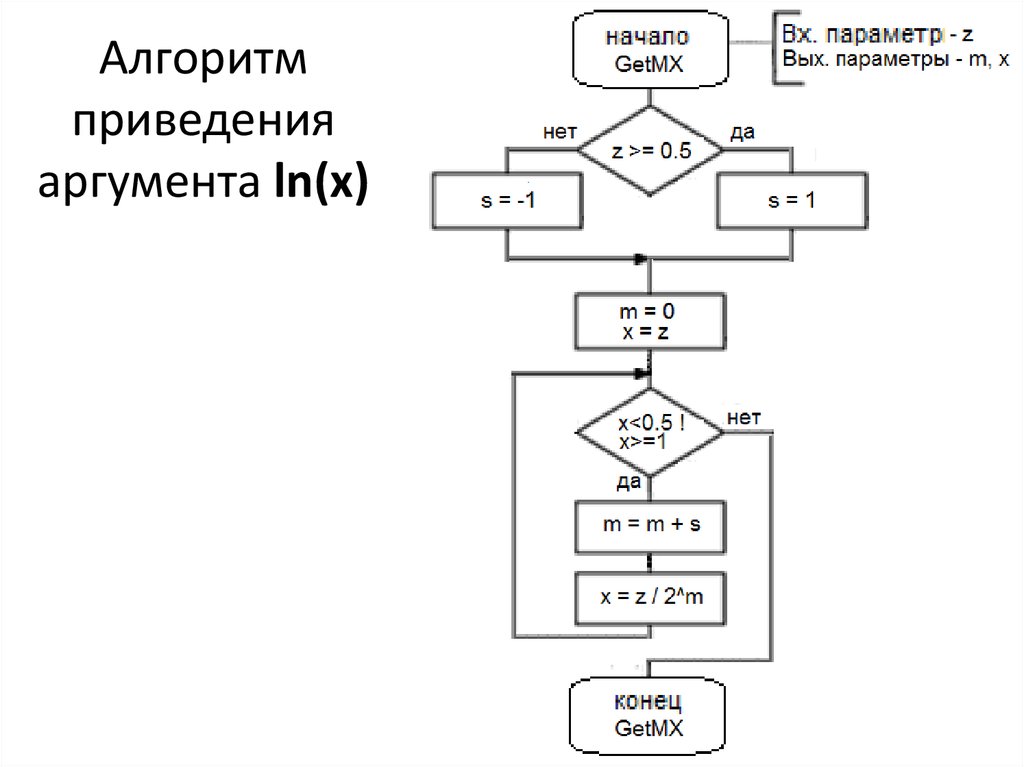
19. Алгоритм приведения аргумента ln(x)

20. Схема алгоритма вычисления ln x

21. Рекуррентные формулы для рядов sinh(x) и cosh(x)

x 2k 1
x 3 x5
1
sinh x ak
x ... ; | x | ; R n (x) | an |
3! 5!
3
k 0
k 0 (2 k 1)!
n
n
x2
ak a k-1
; k 1, 2, 3, ; a 0 x
2 k(2 k 1)
s k s k 1 ak ; k 1, 2, 3, ; s 0 x
x2k
x 2 x4
2
cosh x ak
1 ... ; | x | ; R n (x) an
2! 4!
3
k 0
k 0 (2 k)!
n
n
2
x
ak a k-1
; k 1, 2, 3, ; a 0 1
(2 k 1)2 k
s k s k 1 ak ; k 1, 2, 3, ; s 0 1

22. Свойства функций sinh(x) и cosh(x)

Четность–нечетность
sinh(-x) = -sinh(x)
e e
sinh x
2
x
x
cosh(-x) = cosh(x)
e e
cosh x
2
x
x

23. Многочленные приближения ex и ln x

ex ≈ a0x7+a1x6+a2x5+a3x4+a4x3+a5x2+a6x+a7
a0 = 0,0002040
a3 = 0,0416350
a6 = 1,0
a1 = 0,0014393
a4 = 0,1666674
a7 = 0,9999998
|x| <= 1
Δ = 2∙10-7
a2 = 0,0083298
a5 = 0,5000063
ln(1+x) ≈ a0x7+a1x6+a2x5+a3x4+a4x3+a5x2+a6x+a7
a0 = 0,010757369 a1 = -0,055119959 a2 = 0,134639267
a3 = -0,225873284 a4 = 0,328233122 a5 = -0,499470150
a6 = 0,999981028 a7 = 0
|x| <= 1
Δ = 2∙10-7

24. Многочленные приближения sin x и cos x

sin x ≈ a0x9+a2x7+a4x5+a6x3+a8x
a0 = 0,000002608 a2 = -0,000198107 a4 = 0,008333075
a6 = -0,166666589 a8 = 1,000000002
|x| <= π/2
Δ = 6∙10-9
cos x ≈ a0x10+a2x8+a4x6+a6x4+a8x2+a10
a0 = -0,000000269591
a4 = -0,001388885683
a8 = -0,499999999942
|x| <= 1
Δ = 2∙10-9
a2 = 0,000024795132
a6 = 0,041666665950
a10 = 1,0

25. Многочленное приближение tg x

tg x ≈ a0x13+a2x11+a4x9+a6x7+a8x5+a10x3+a12x
a0 = 0,0095168091 a2 = 0,0029005250 a4 = 0,0245650893
a6 = 0,0533740603 a8 = 0,1333923995 a10 = 0,3333314036
a12 = 1,0
|x| <= π/4
Δ = 2∙10-8

26. Вычисление функций методом итераций

Всякую функцию y = f(x) можно различными способами
задавать неявно, т.е. некоторым уравнением F(x,y) = 0, где
x – заданный параметр, а y - неизвестное.
y n 1 y n
F(x, y n )
; n 0,1,2,...
F' (x, y n )
F(x, y 0 )
y 0 ; y1 y 0
F' (x, y 0 )
y 2 y1
F(x, y 1 )
F' (x, y 1 )
………………………….
Условия сходимости: F'(x,y) и F''(x,y) существуют и
знакопостоянны в окрестности корня уравнения
Правило останова: |yn+1 - yn| < ε – допустимая абс. погр.

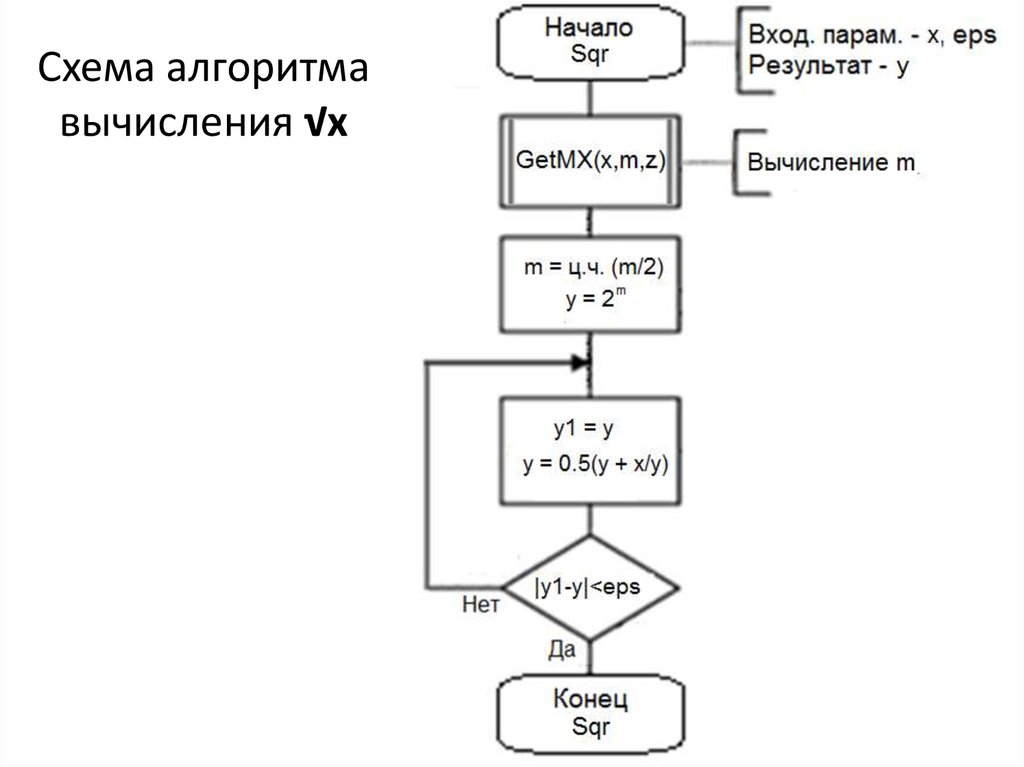
27. Вычисление квадратного корня методом итераций

Пусть y = √x (x > 0). Тогда F(x,y) = y2 – x
y n 1
1
x
(y n ); n 0, 1, 2 ...
2
yn
Эта формула называется формулой Герона.
Выбор y0:
Если x>1, то x = 2mz, где m – целое число и 0,5≤z<1,
и y0 = 2E(m/2), где E(m/2) – целая часть числа m/2.
Если 0,01≤x≤1, то y0 = ax+b, a и b – из таблицы:
Интервал x
a
b
Интервал x
a
b
(0,01 ; 0,02)
4,1
0,060
(0,18 ; 0,30)
1,0
0,247
(0,02 ; 0,03)
3,2
0,078
(0,30 ; 0,60)
0,8
0,304
(0,03 ; 0,08)
2,2
0,110
(0,60 ; 1,00)
0,6
0,409
(0,08 ; 0,18)
1,4
0,174

28. Схема алгоритма вычисления √x

29. Вычисление корня p–й степени методом итераций

Пусть y = p√x (x > 0, p>0). Тогда
F(x,y) = 1 – x/yp
p
1 yn
y n 1 y n (1 ) ; n 0, 1, 2 ...
p px
Выбор y0
y x(p 1) , откуда
p
0
y0 e
ln x(p 1)
p

30. Вычисление корня p–й степени методом итераций. Формула Ньютона

Если преобразовать выражение y = p√x к виду
F(x,y) = yp– x, то получим другую
итерационную формулу:
y n 1
1
x
(p 1) y n p 1 ; n 0, 1, 2 ...
p
yn
известную как формула Ньютона. При p = 2
из формулы Ньютона получается формула
Герона.