Прямая в системе H, V, W (Лекция 2)

1.

Лекция № 2
1

2.

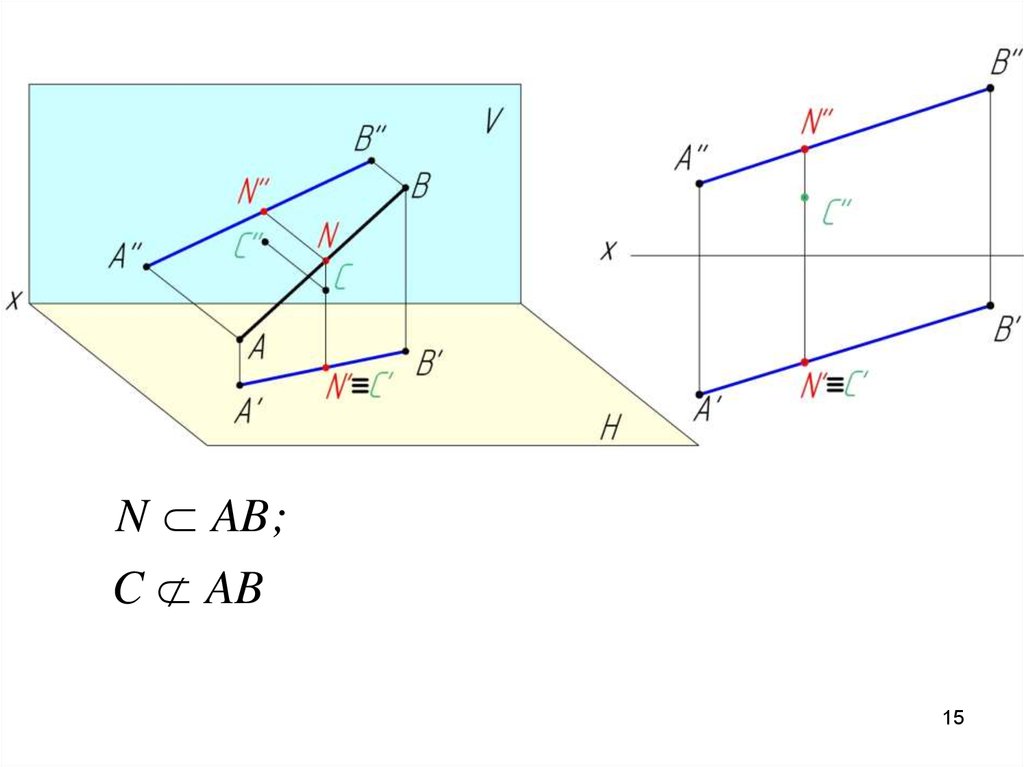
2.1. Проекции прямой.
Принадлежность точки прямой.
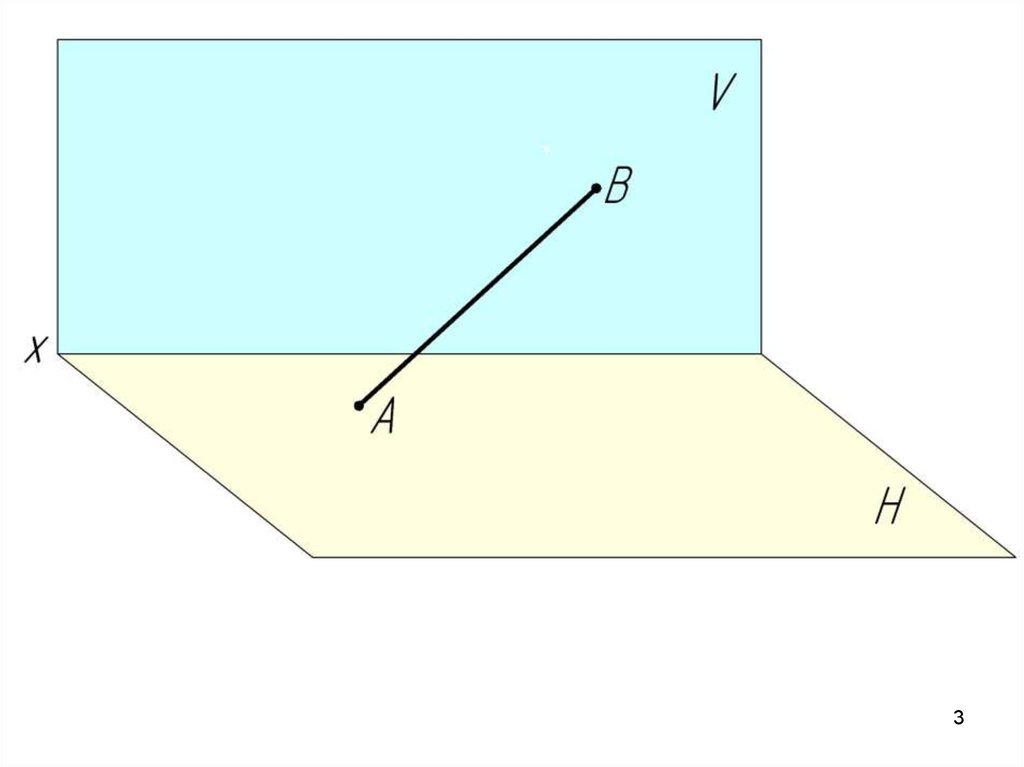
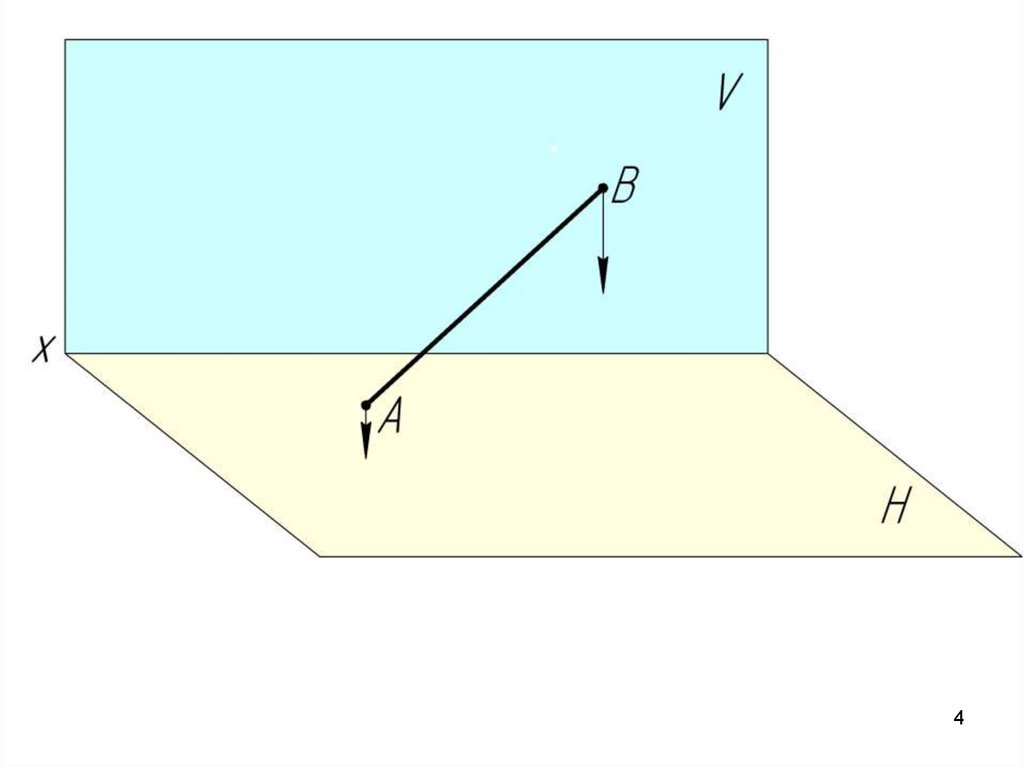
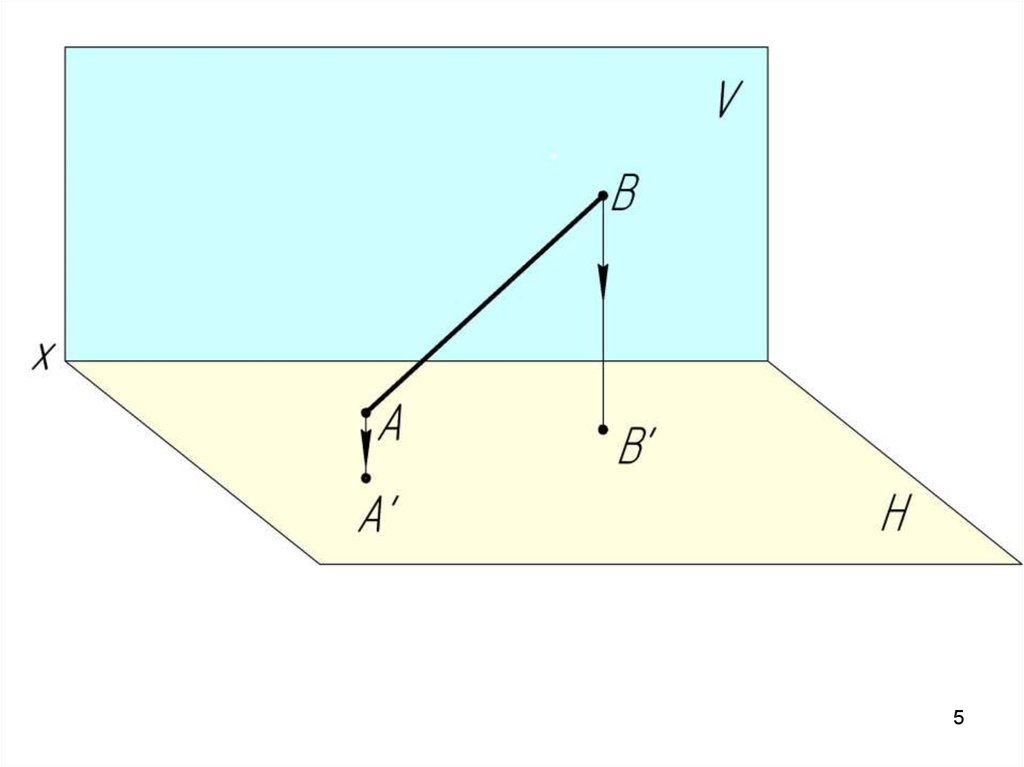
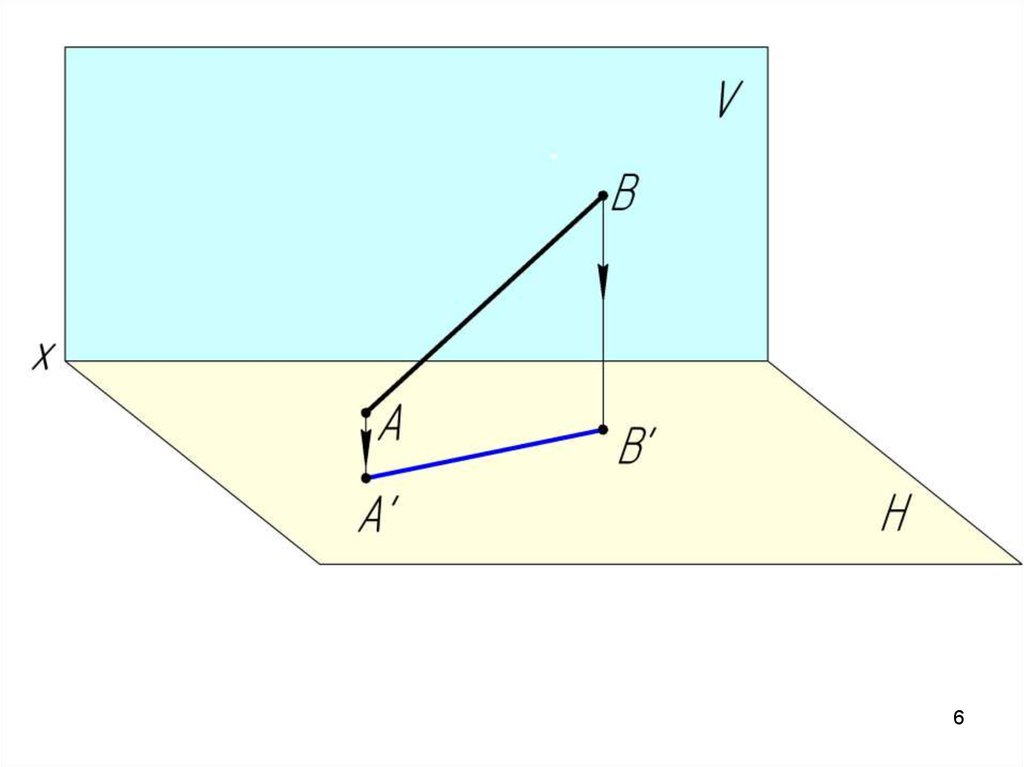
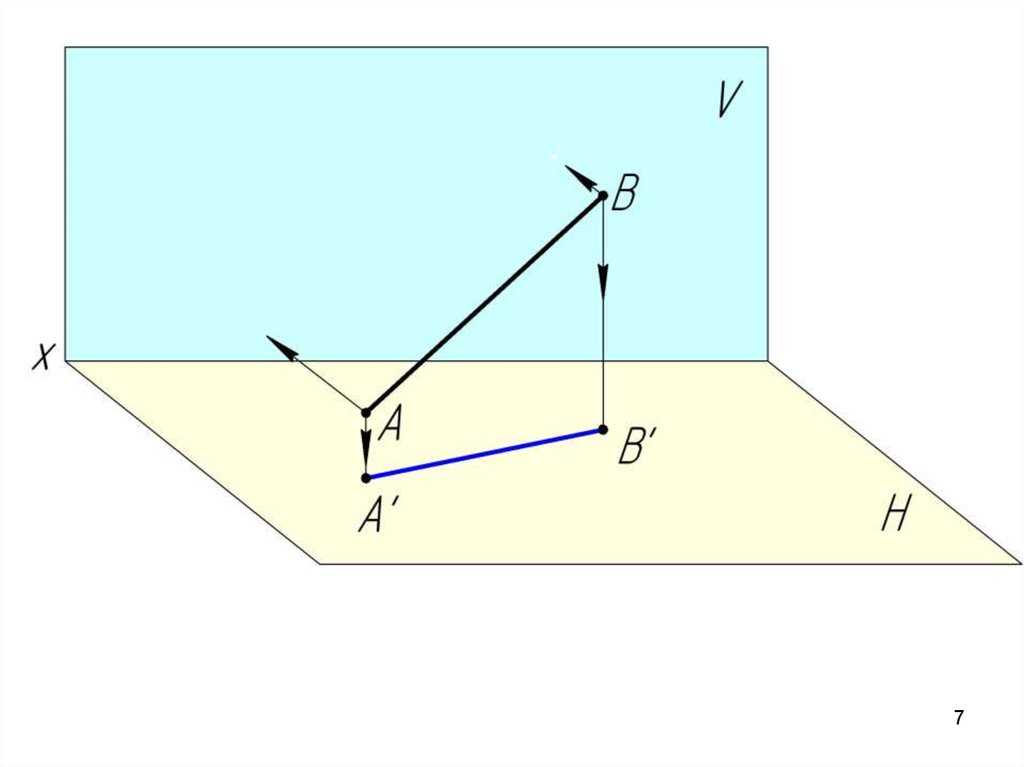
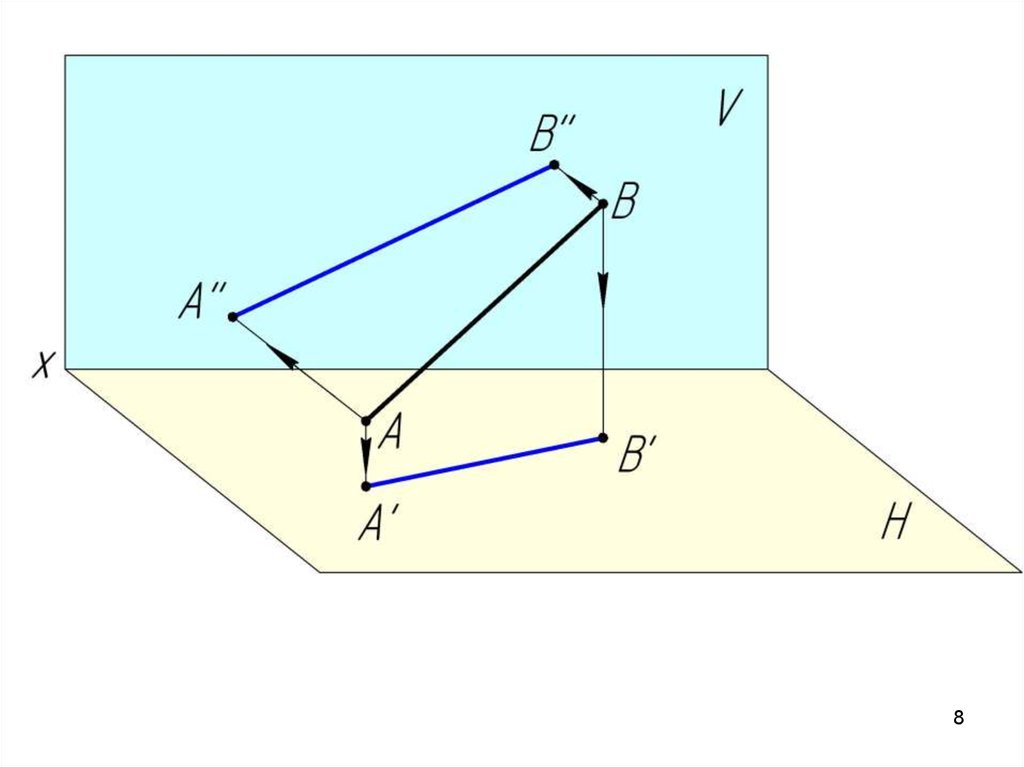
Проекция прямой линии – есть прямая.
2

3.

3

4.

4

5.

5

6.

6

7.

7

8.

8

9.

9

10.

10

11.

11

12.

12

13.

13

14.

14

15.

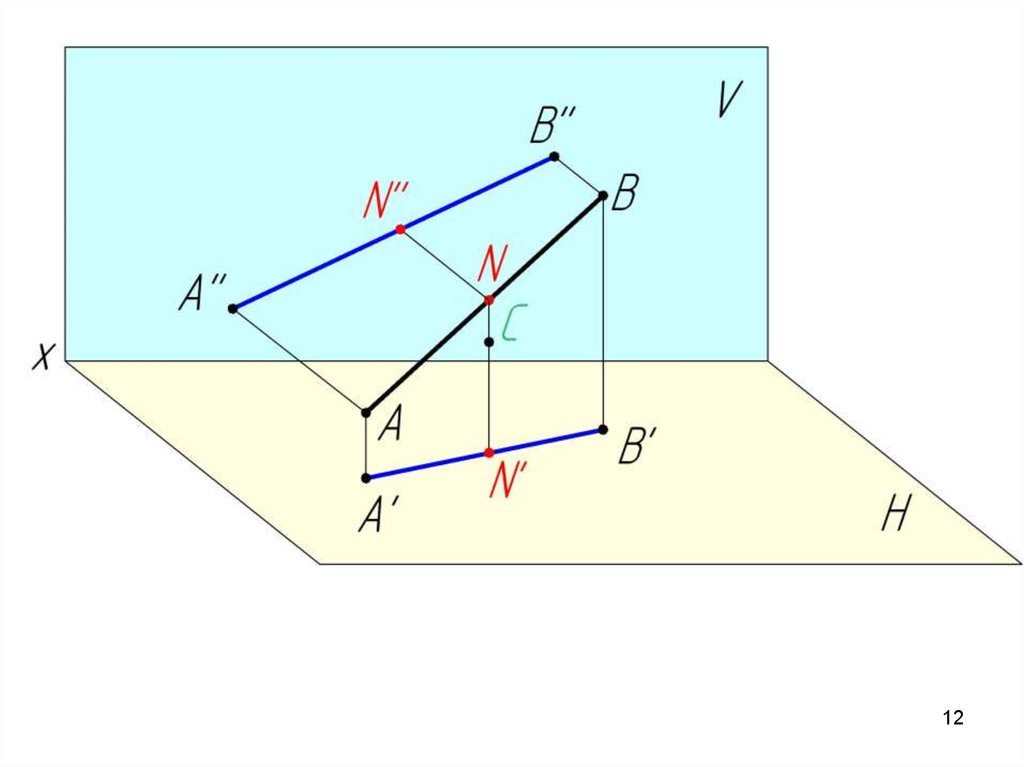
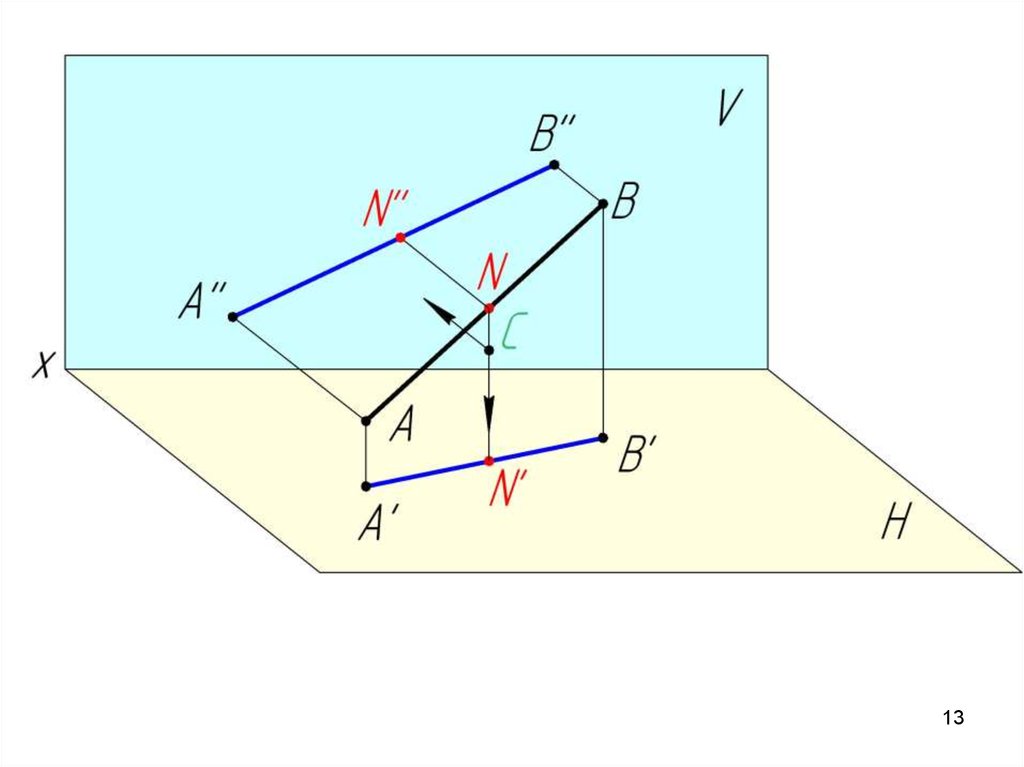
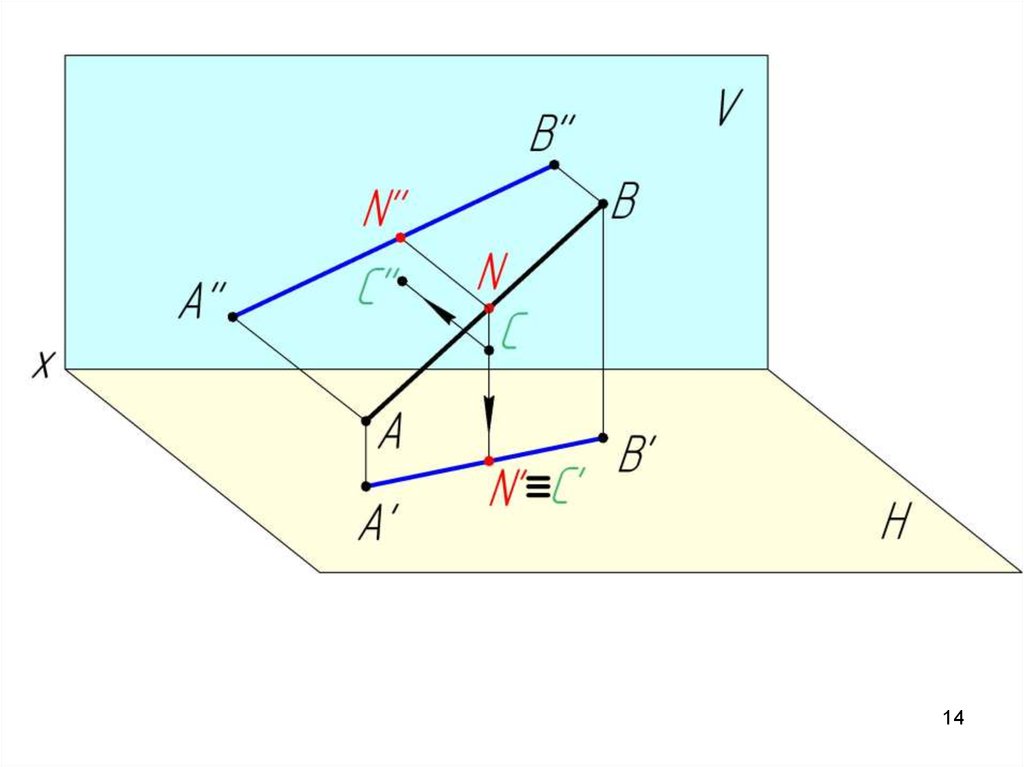
N AB ;
C AB
15

16.

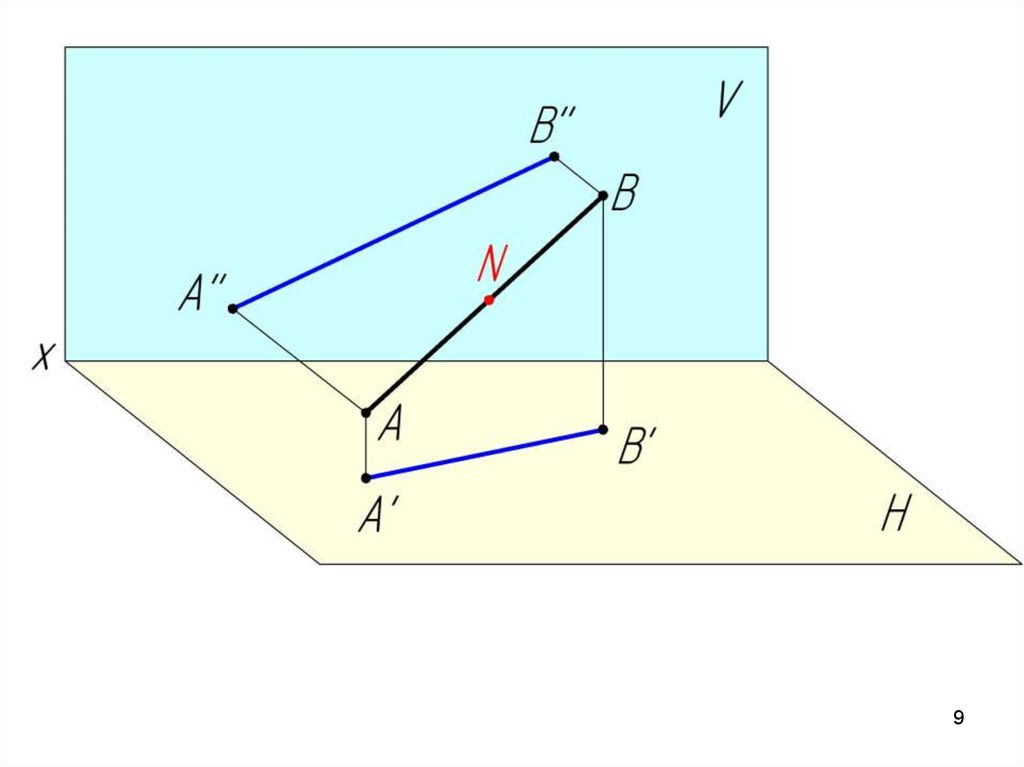
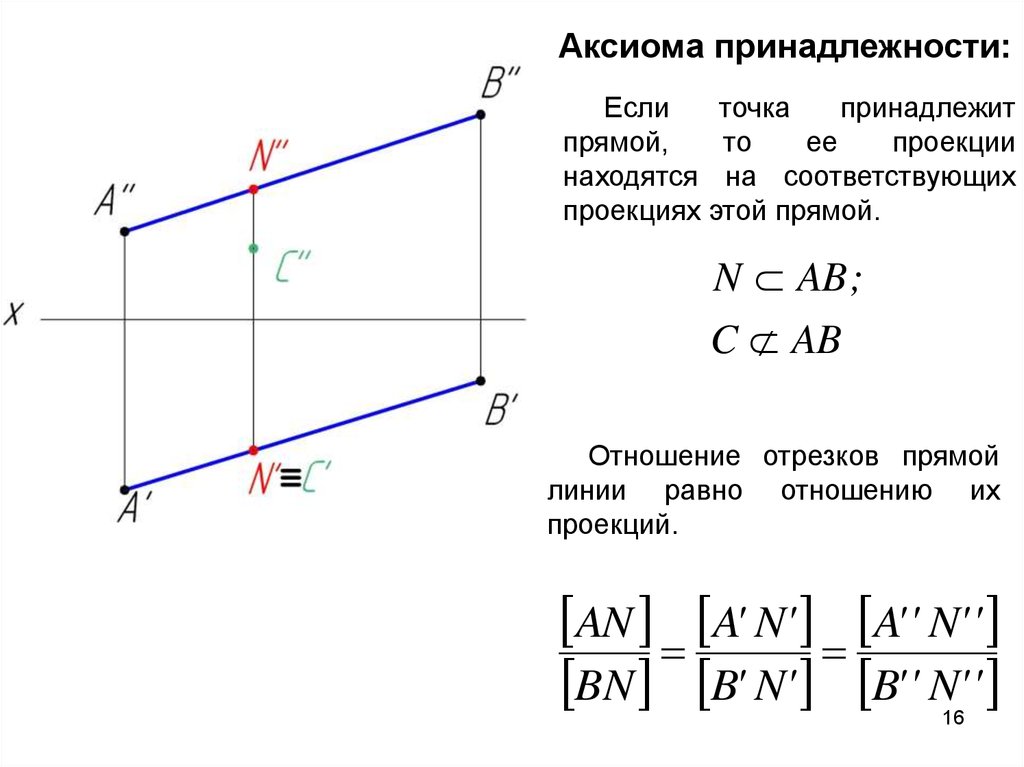
Аксиома принадлежности:
Если
точка
принадлежит
прямой,
то
ее
проекции
находятся на соответствующих
проекциях этой прямой.
N AB ;
C AB
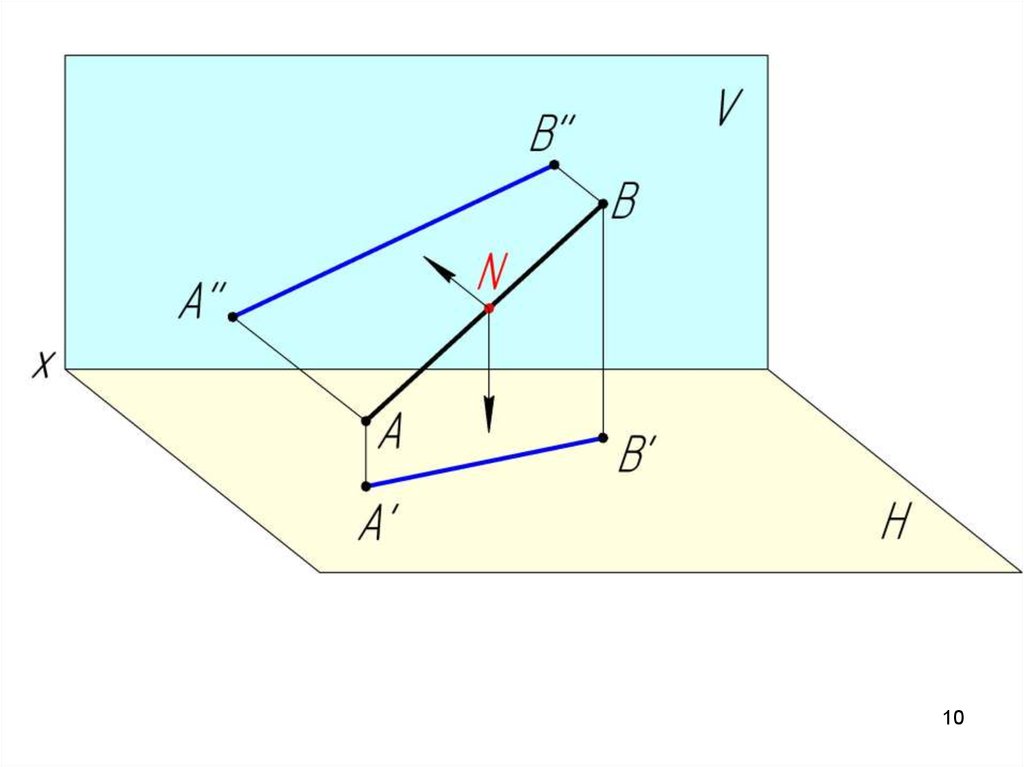
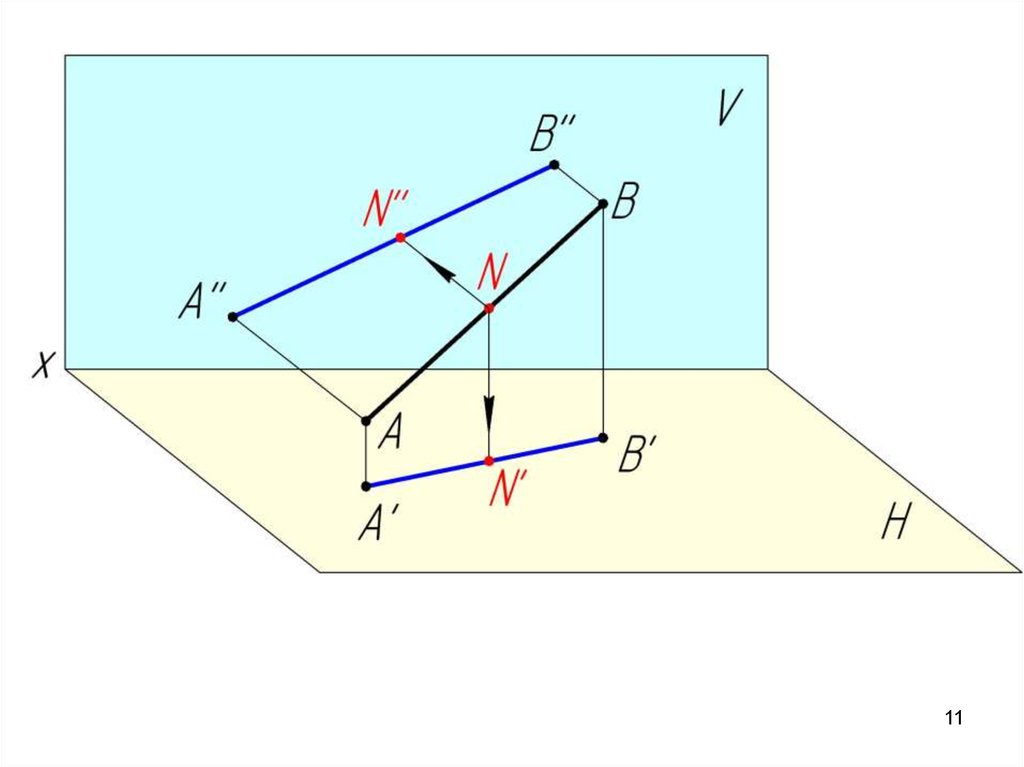
Отношение отрезков прямой
линии равно отношению их
проекций.
AN A' N' A' ' N' '
BN B' N' B' ' N' '
16

17.

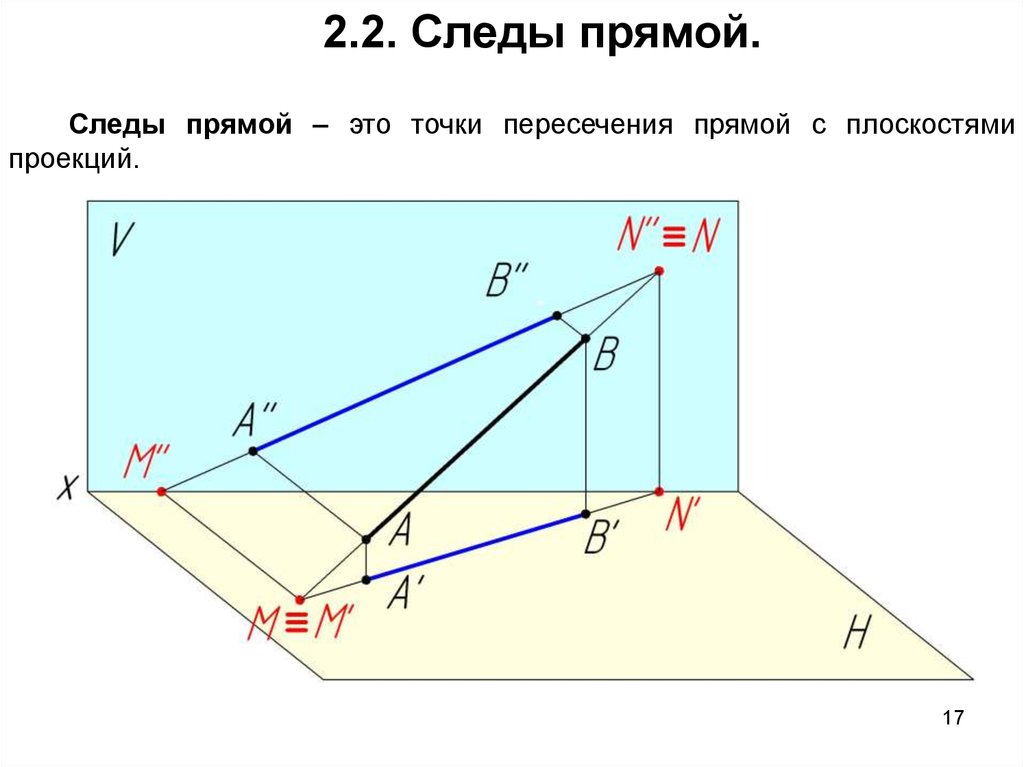
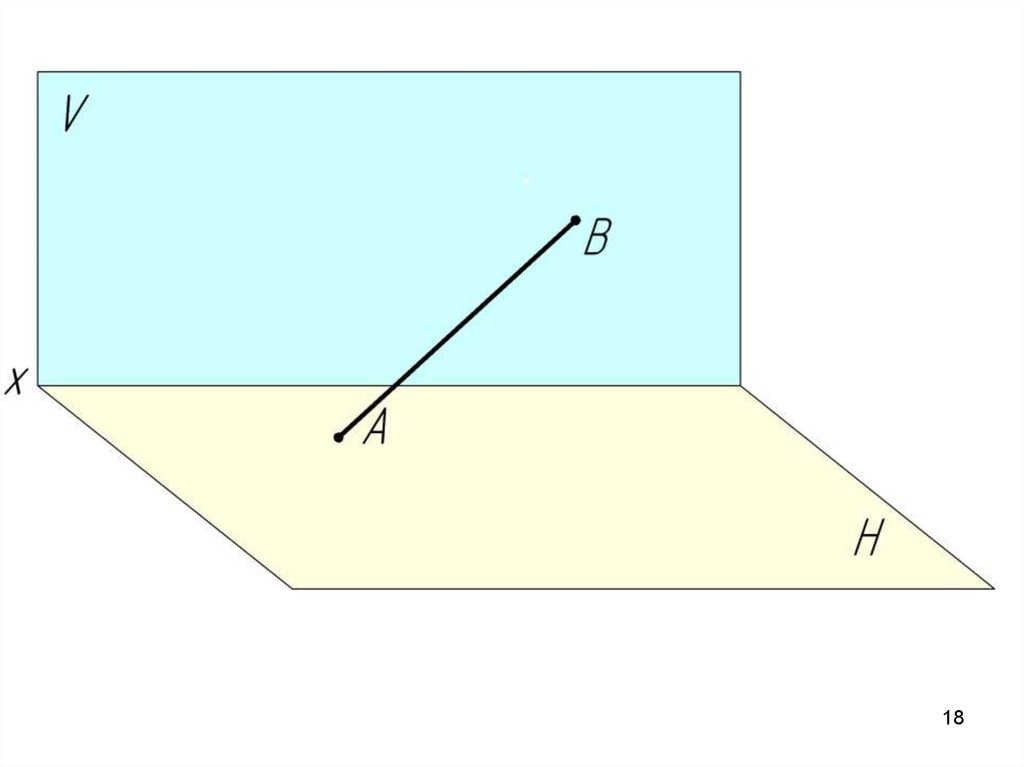
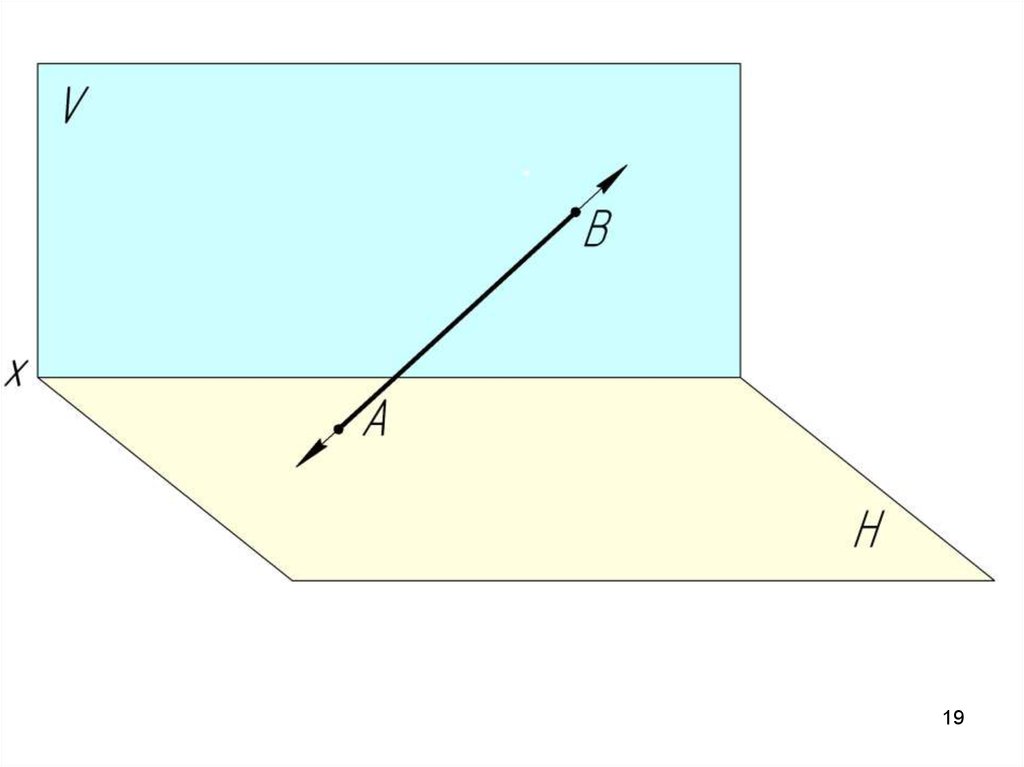
2.2. Следы прямой.
Следы прямой – это точки пересечения прямой с плоскостями
проекций.
17

18.

18

19.

19

20.

20

21.

21

22.

22

23.

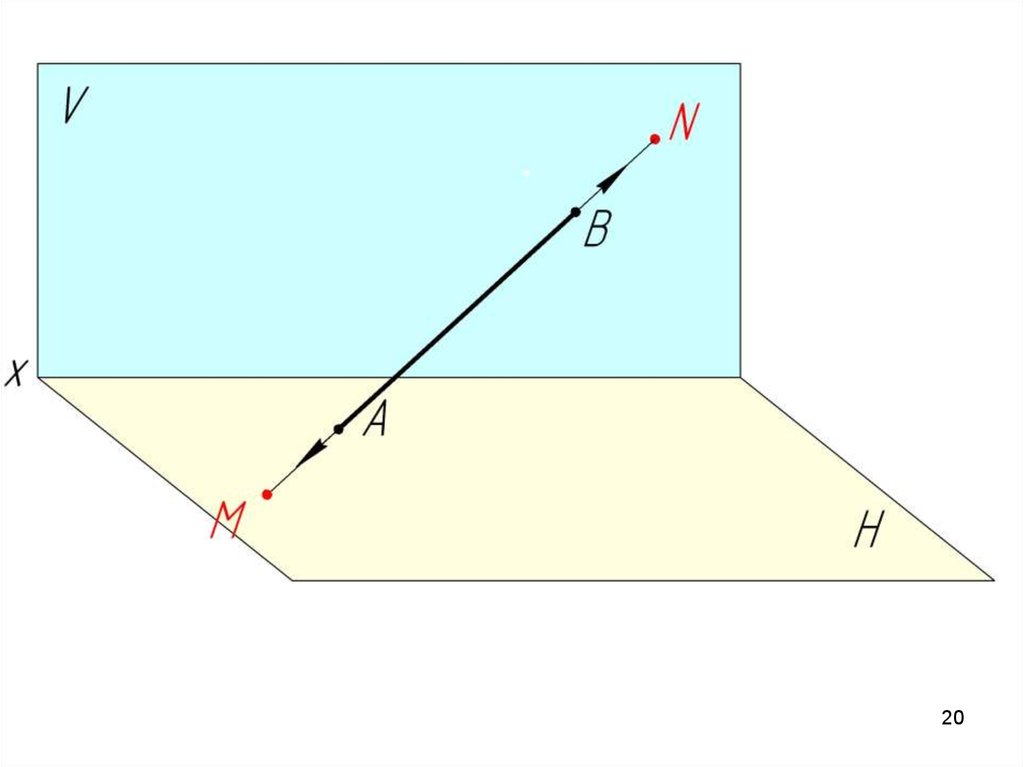
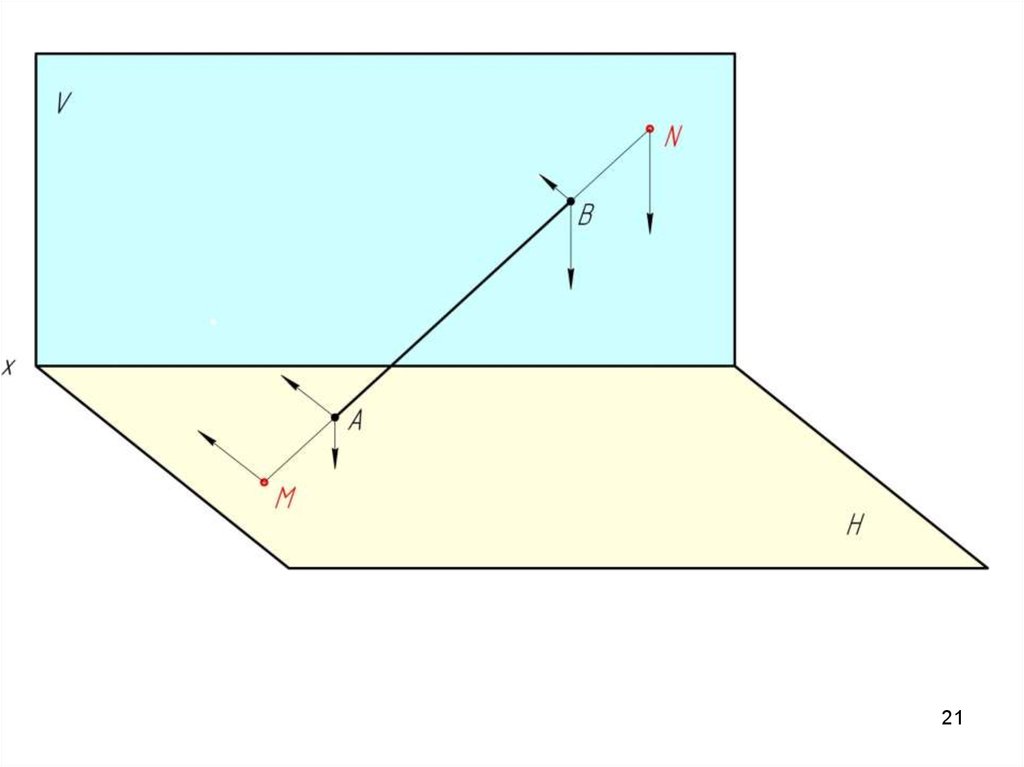
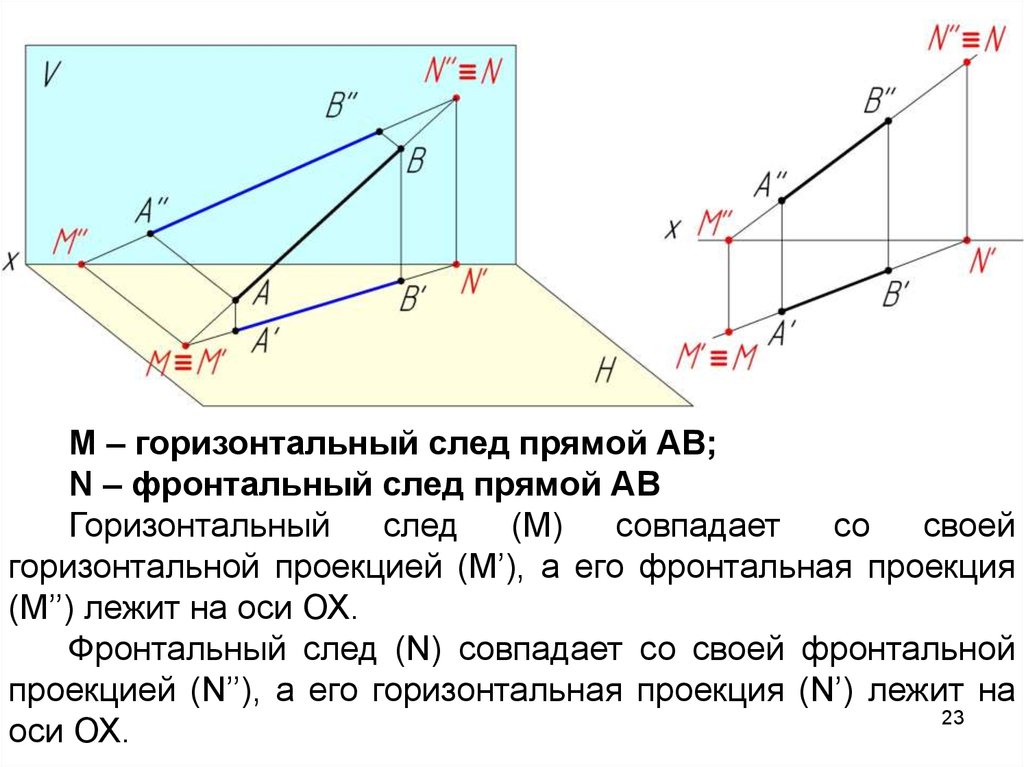
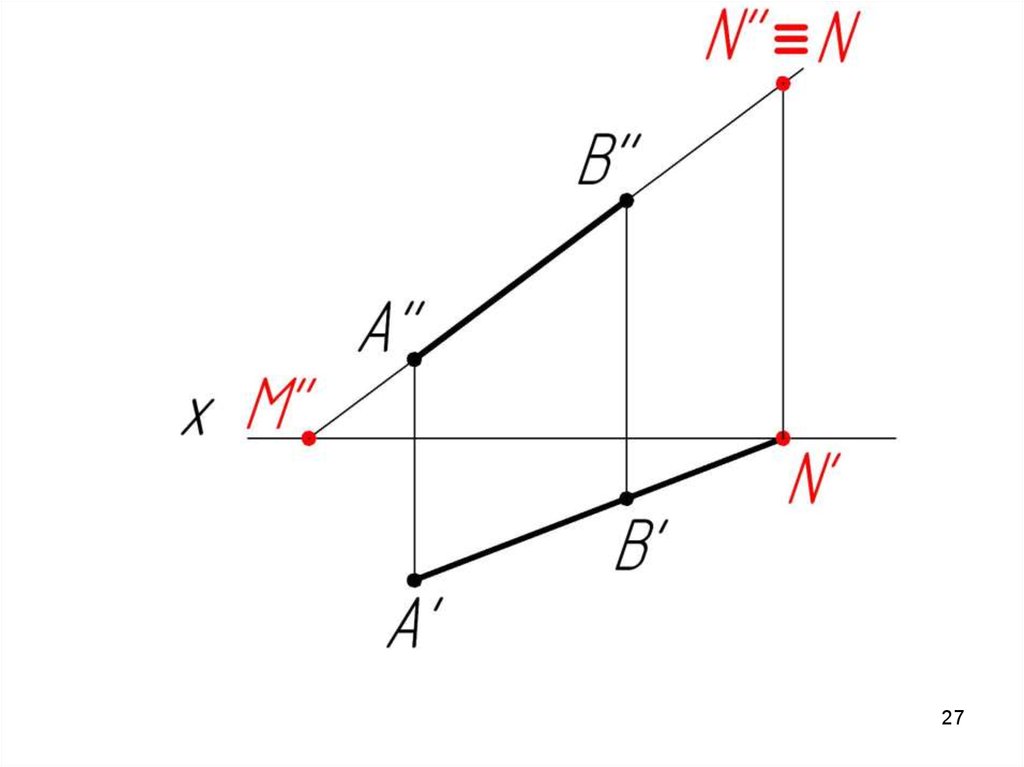
М – горизонтальный след прямой АВ;
N – фронтальный след прямой АВ
Горизонтальный
след
(М)
совпадает
со
своей
горизонтальной проекцией (М’), а его фронтальная проекция
(М’’) лежит на оси ОХ.
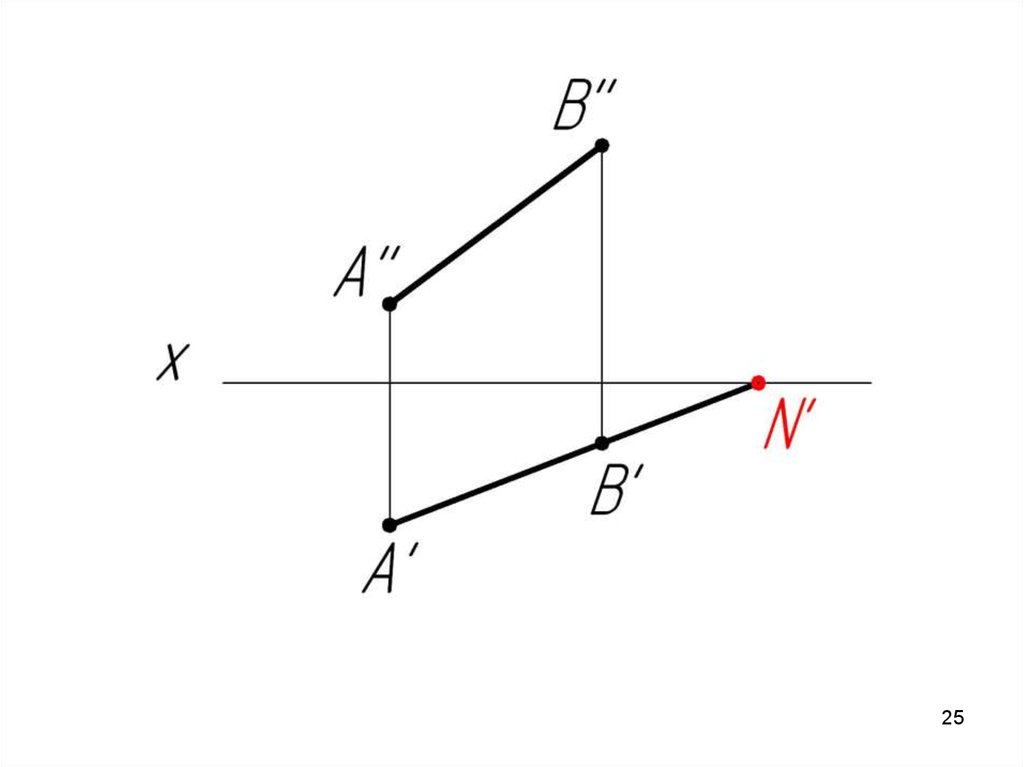
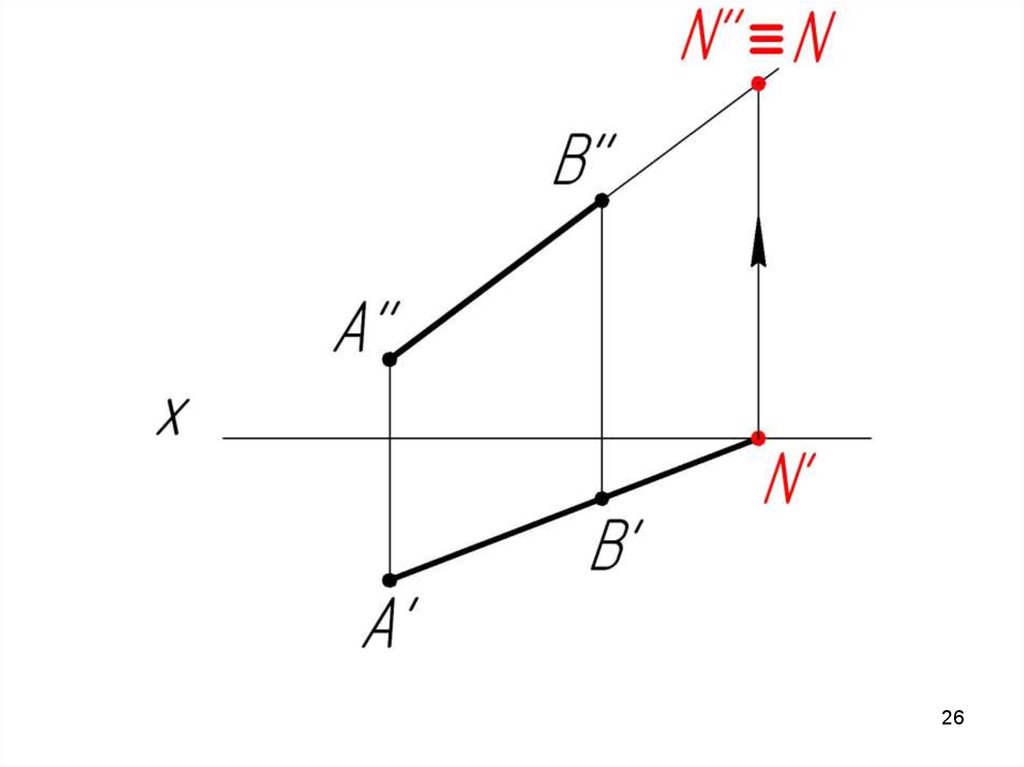
Фронтальный след (N) совпадает со своей фронтальной
проекцией (N’’), а его горизонтальная проекция (N’) лежит на
23
оси ОХ.

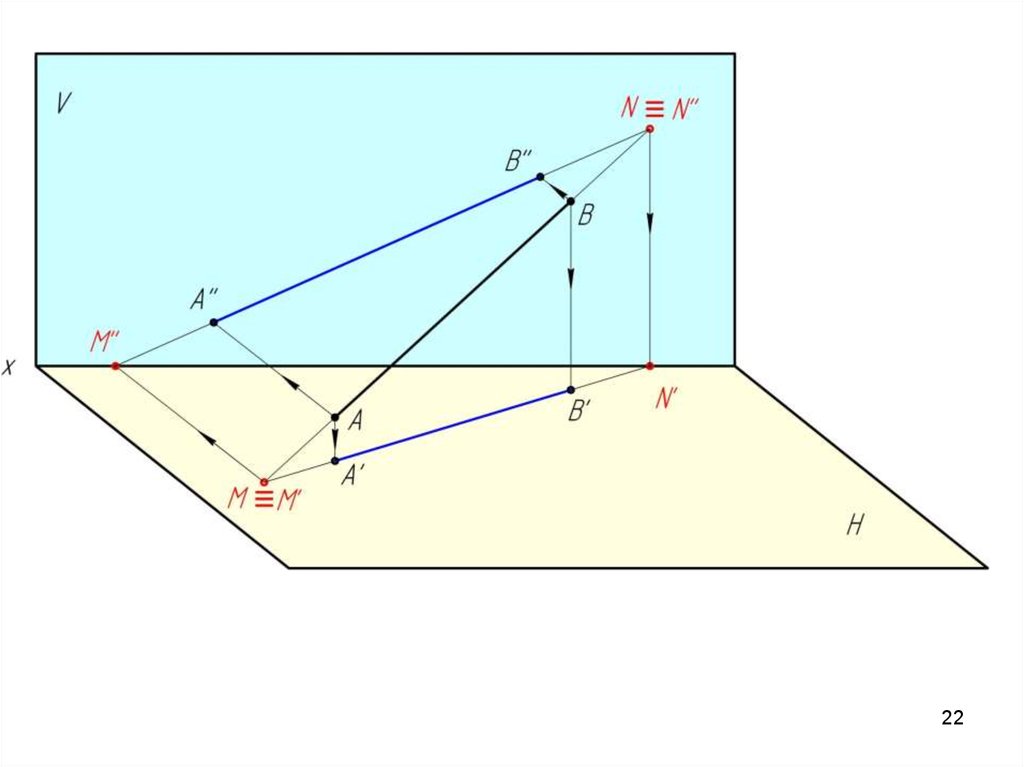
24.

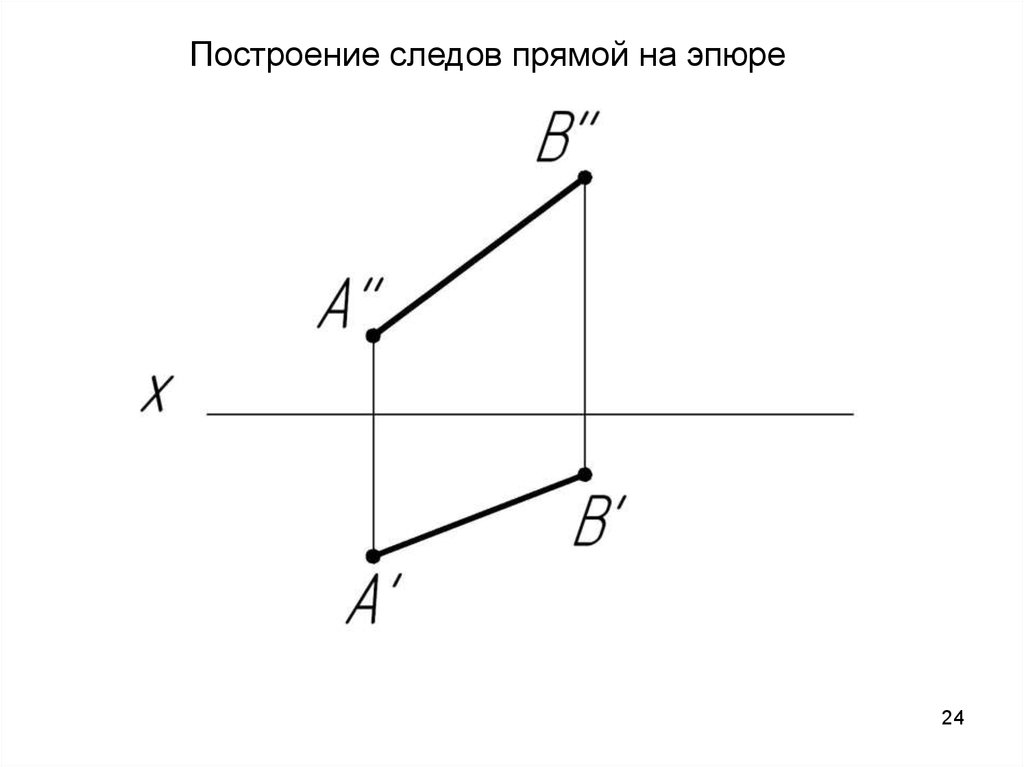
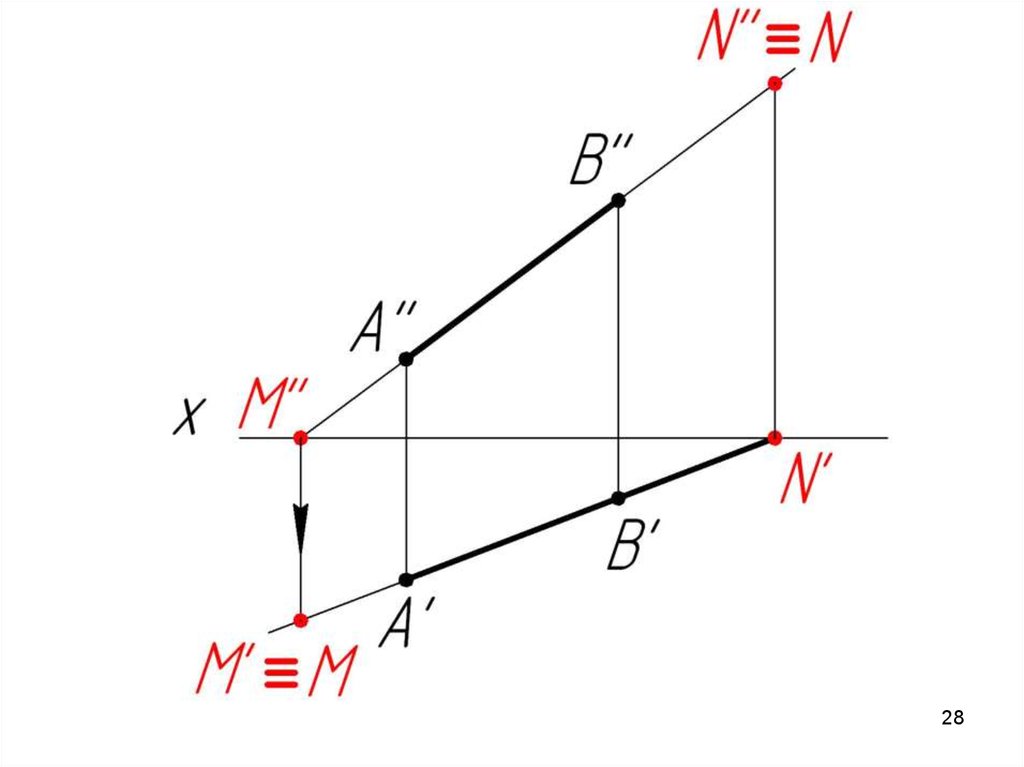
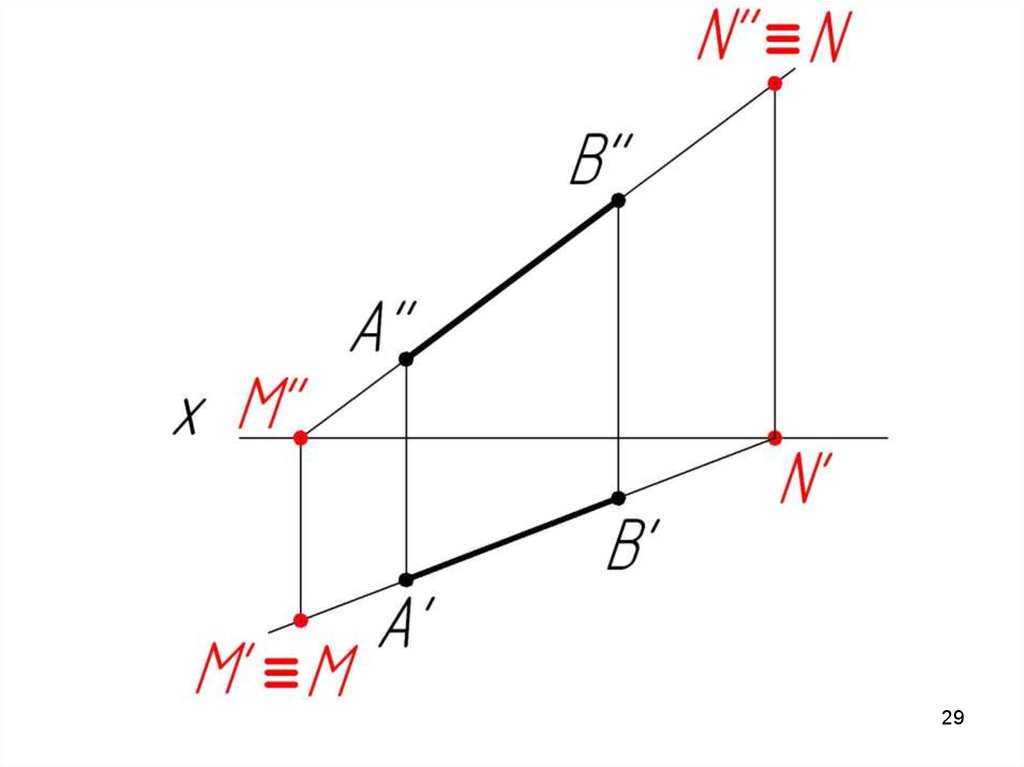
Построение следов прямой на эпюре
24

25.

25

26.

26

27.

27

28.

28

29.

29

30.

2.3. Положение прямой относительно
плоскостей проекций.
Прямая по отношению к плоскостям проекций H, V, W
может занимать следующие положения:
1 - общее положение
2 - частное положение:
- прямые уровня;
- проецирующие прямые.
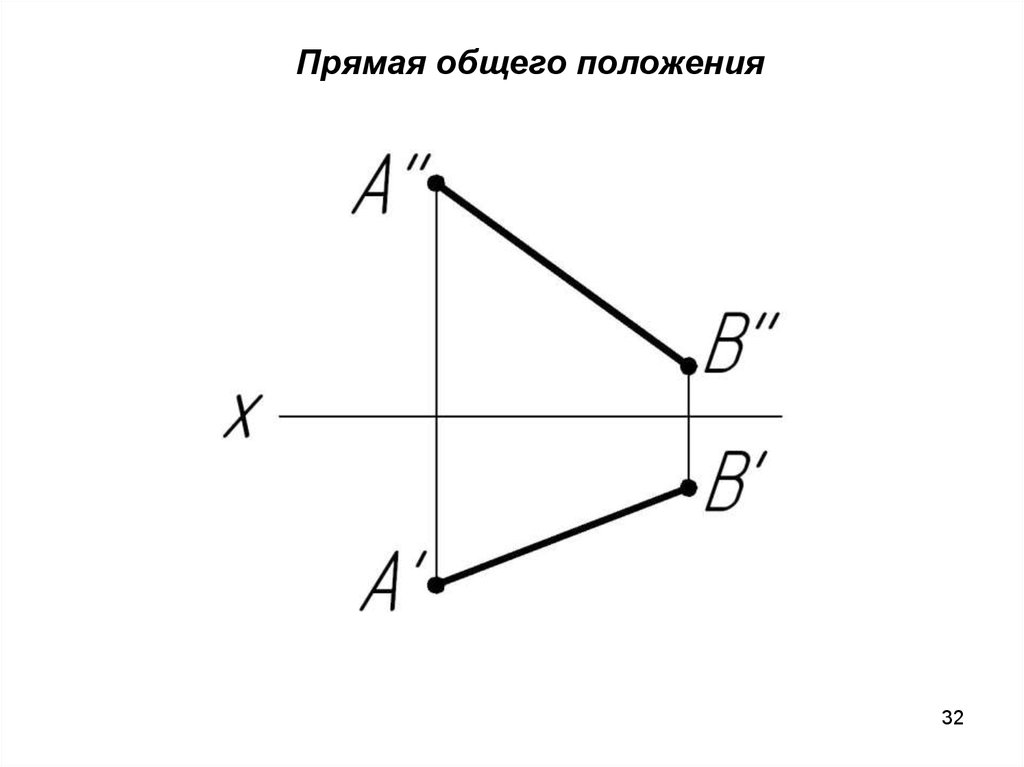
Прямая общего положения – это прямая, которая не
параллельна ни одной из плоскостей проекций.
30

31.

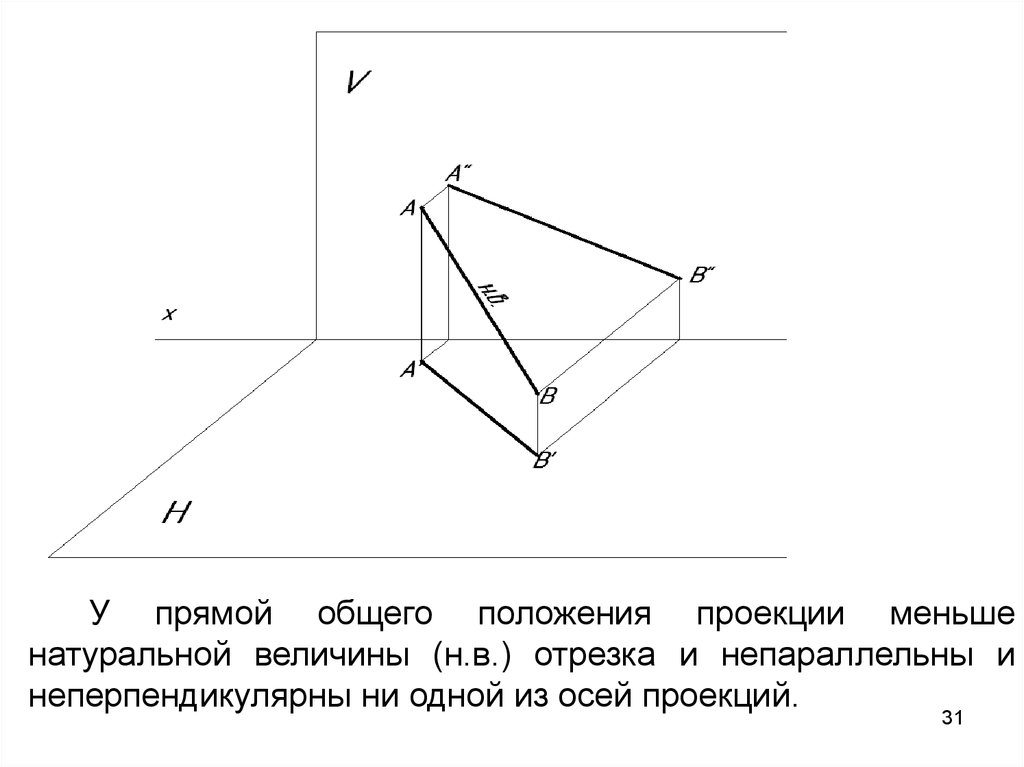
У прямой общего положения проекции меньше
натуральной величины (н.в.) отрезка и непараллельны и
неперпендикулярны ни одной из осей проекций.
31

32.

Прямая общего положения
32

33.

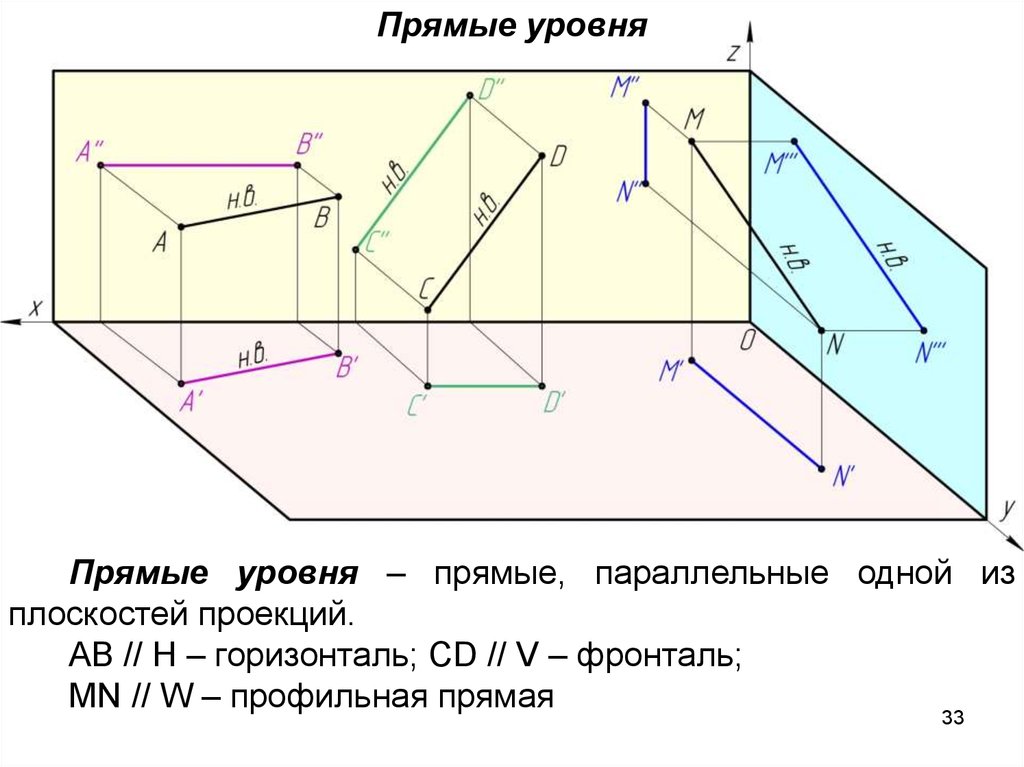
Прямые уровня
Прямые уровня – прямые, параллельные одной из
плоскостей проекций.
AB // H – горизонталь; CD // V – фронталь;
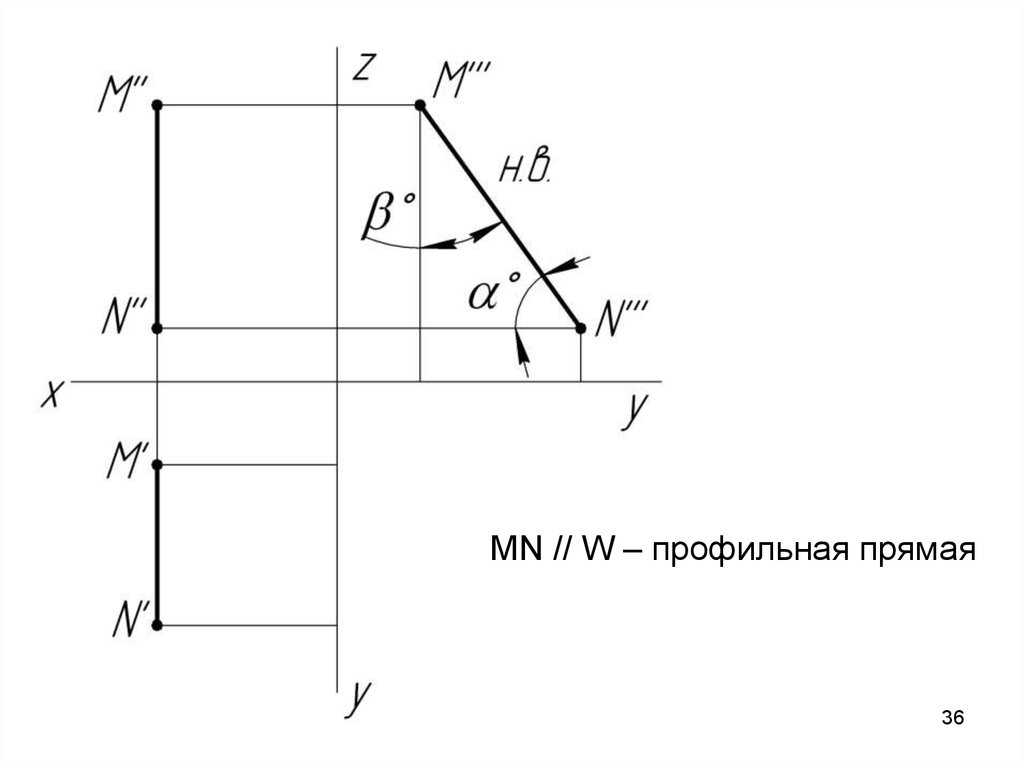
MN // W – профильная прямая
33

34.

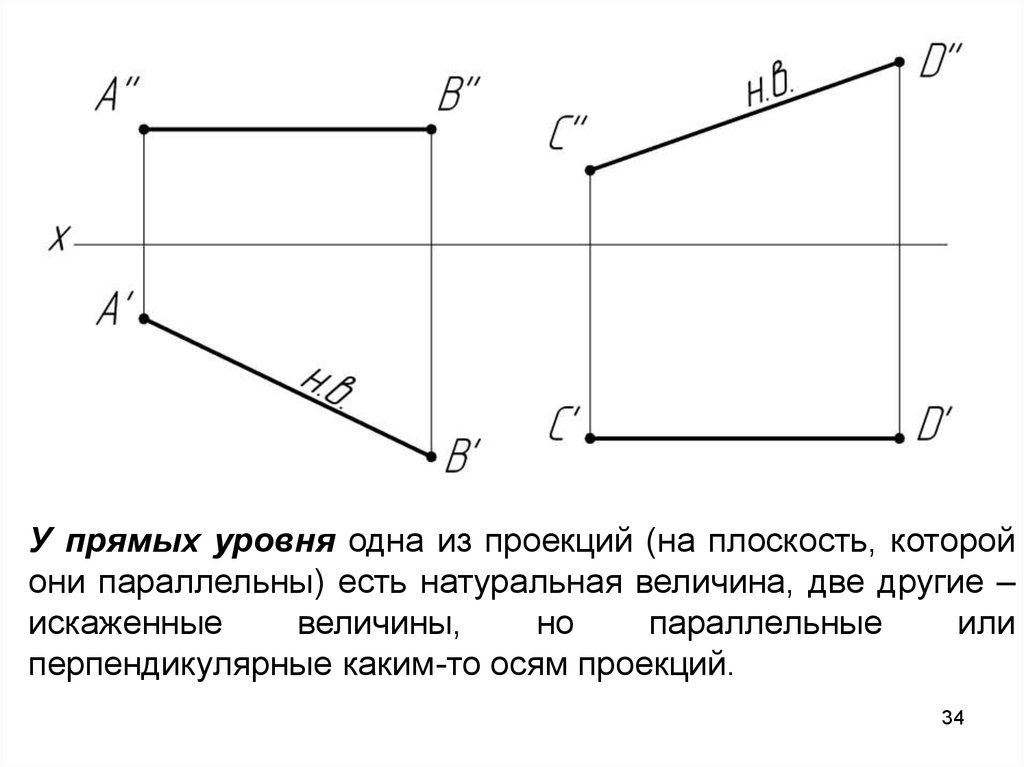
У прямых уровня одна из проекций (на плоскость, которой
они параллельны) есть натуральная величина, две другие –
искаженные
величины,
но
параллельные
или
перпендикулярные каким-то осям проекций.
34

35.

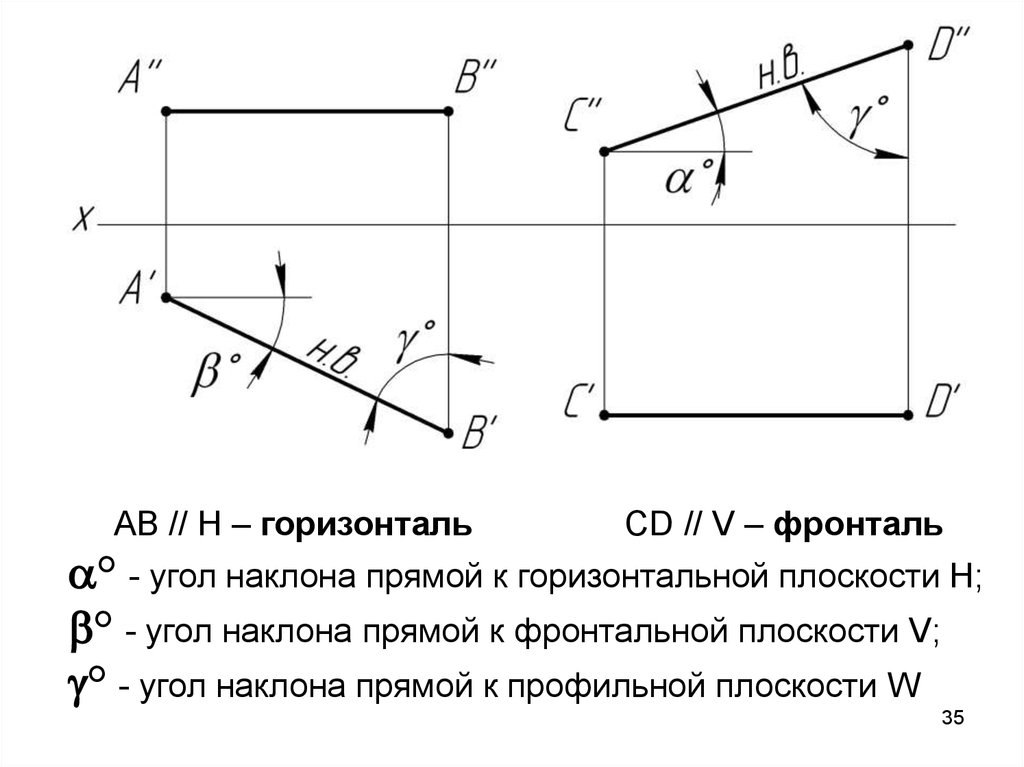
AB // H – горизонталь
CD // V – фронталь
° - угол наклона прямой к горизонтальной плоскости Н;
° - угол наклона прямой к фронтальной плоскости V;
° - угол наклона прямой к профильной плоскости W
35

36.

MN // W – профильная прямая
36

37.

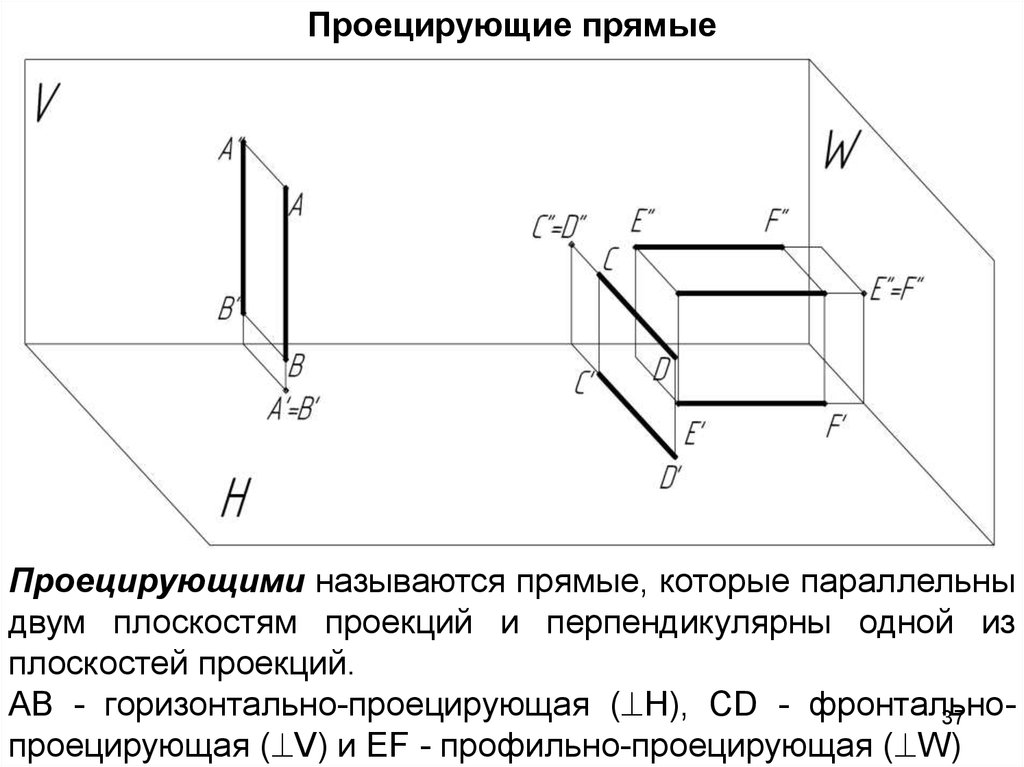
Проецирующие прямые
Проецирующими называются прямые, которые параллельны
двум плоскостям проекций и перпендикулярны одной из
плоскостей проекций.
АВ - горизонтально-проецирующая ( H), CD - фронтально37
проецирующая ( V) и EF - профильно-проецирующая ( W)

38.

AB – горизонтально-проецирующая (AB H)
СD – фронтально-проецирующая (CD V)
У проецирующих прямых одна из проекций (на
плоскость, которой они перпендикулярны) есть точка, две
другие – натуральные величины, но параллельные или
38
перпендикулярные каким-то осям проекций.

39.

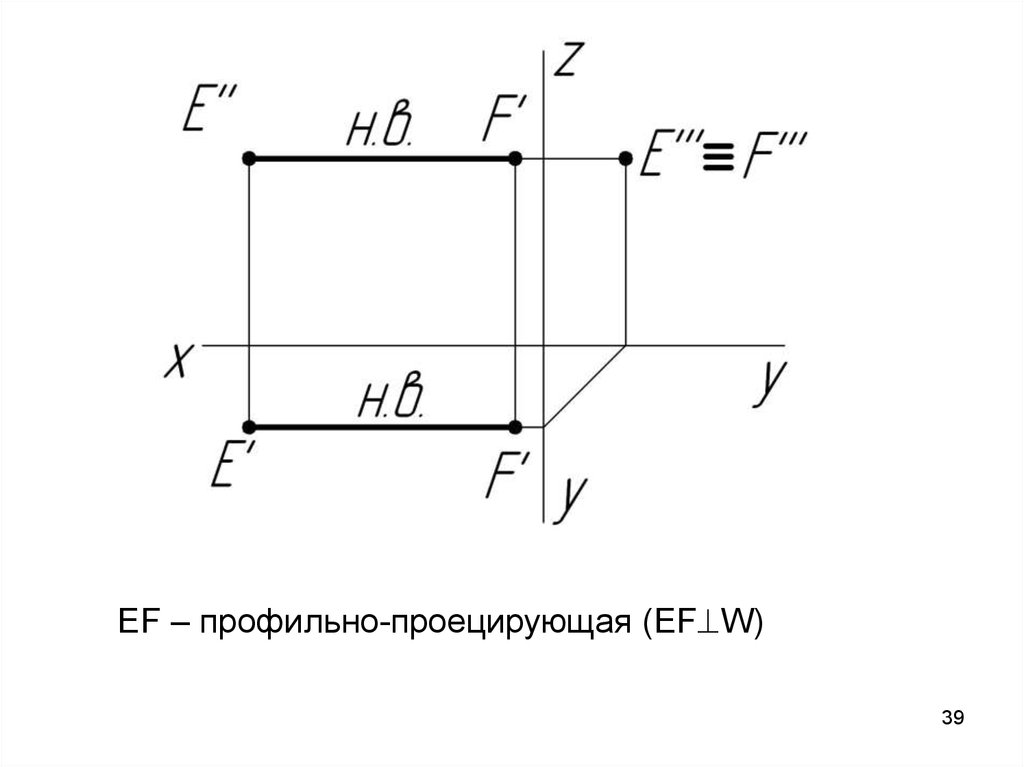
EF – профильно-проецирующая (EF W)
39

40.

2.4. Относительное положение двух
прямых
-
По своему взаимному положению две прямые могут быть:
пересекающимися
параллельными
скрещивающимися.
40

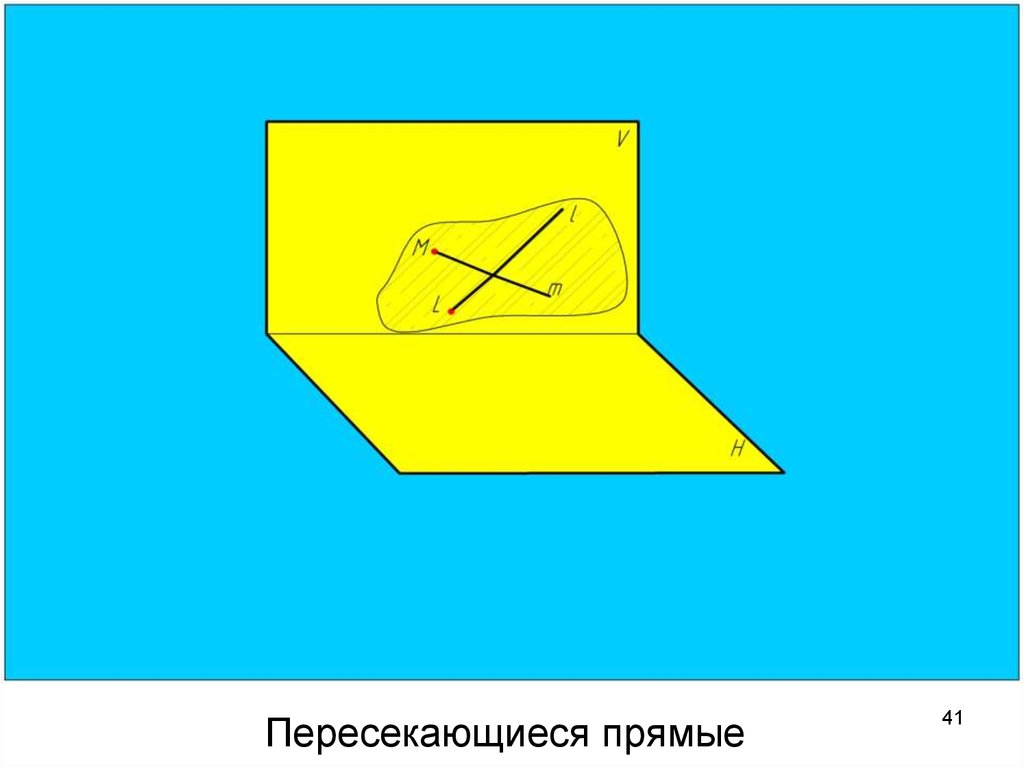
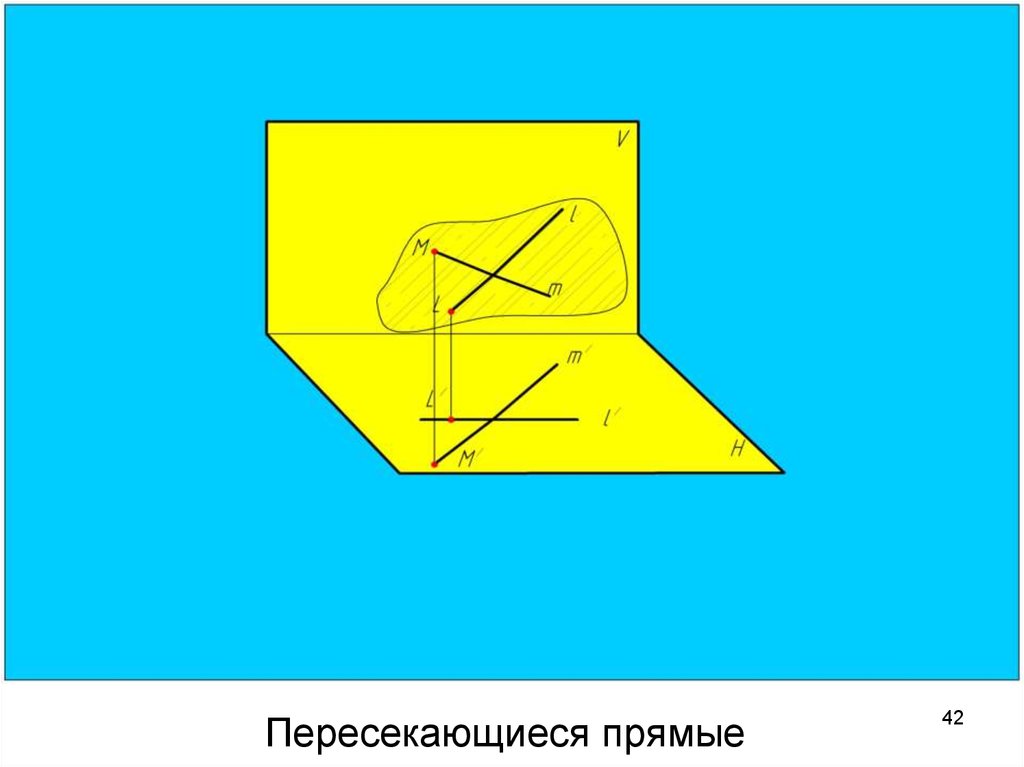
41. Пересекающиеся прямые

41

42. Пересекающиеся прямые

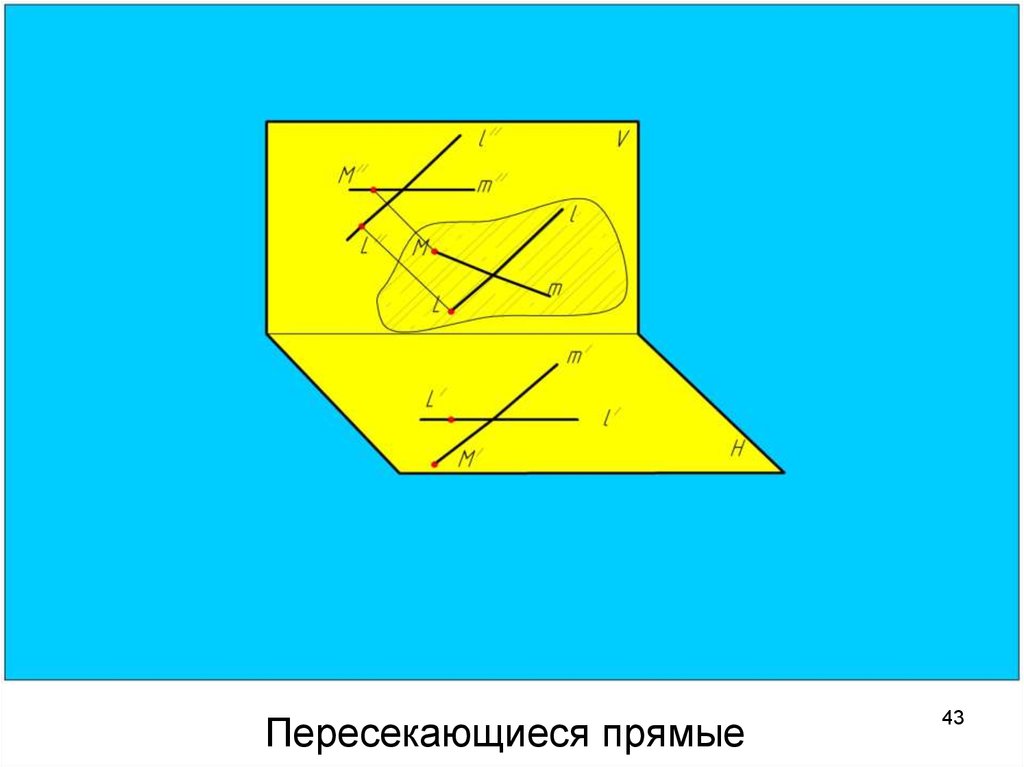
42

43. Пересекающиеся прямые

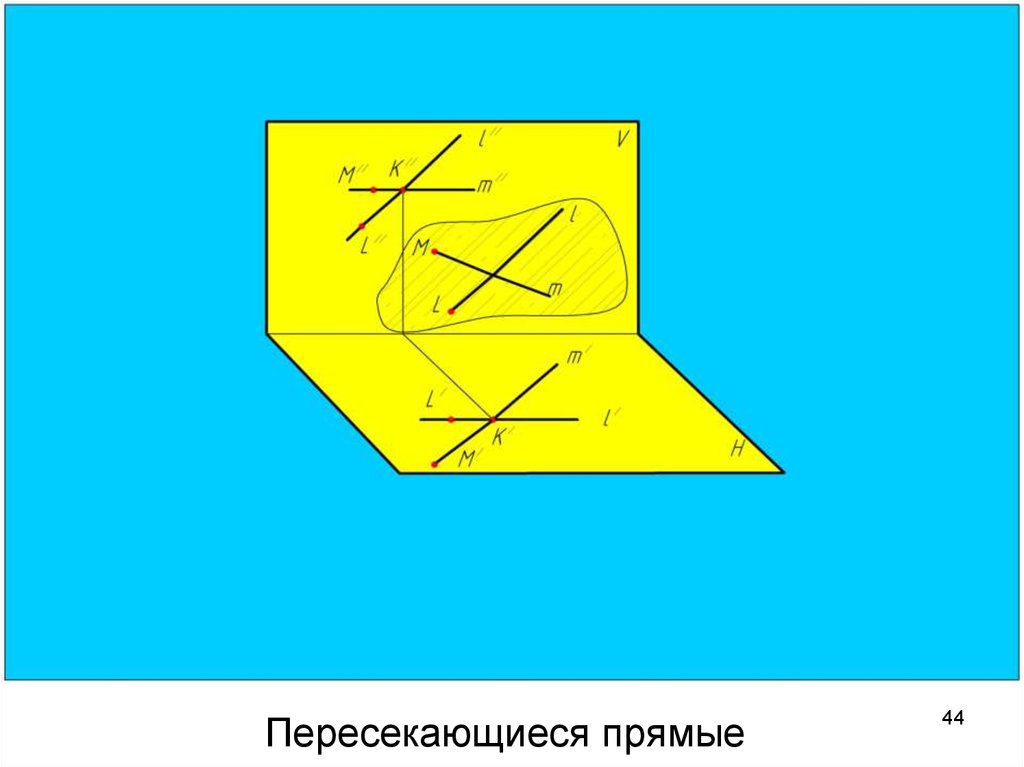
43

44. Пересекающиеся прямые

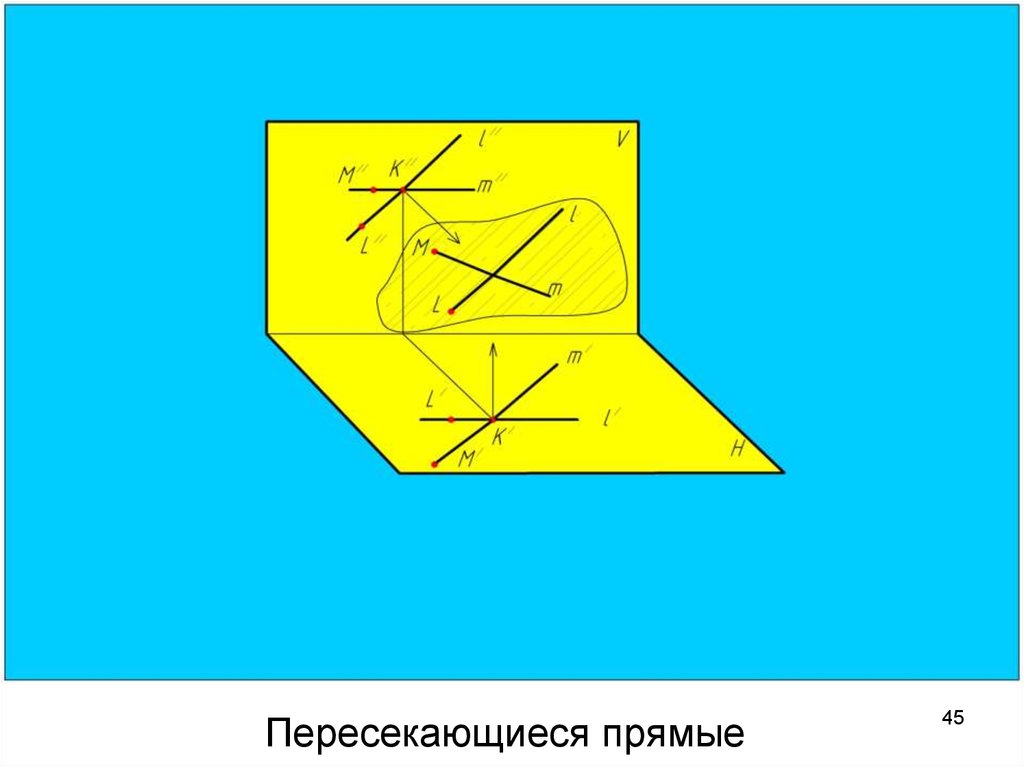
44

45. Пересекающиеся прямые

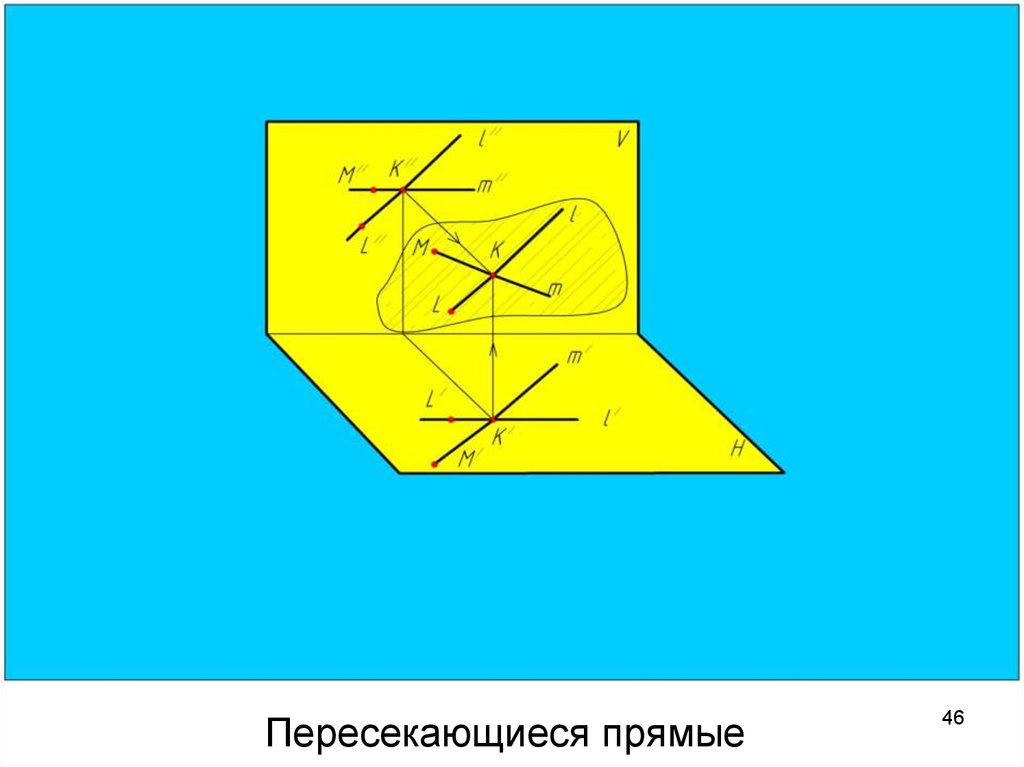
45

46. Пересекающиеся прямые

46

47.

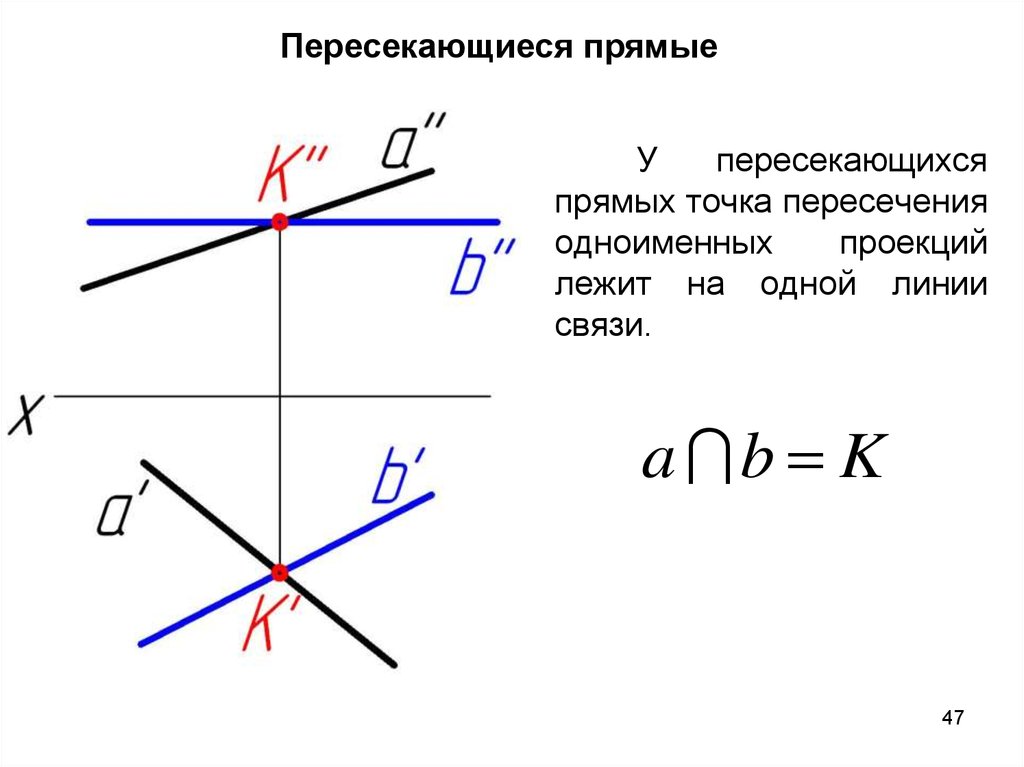
Пересекающиеся прямые
У
пересекающихся
прямых точка пересечения
одноименных
проекций
лежит на одной линии
связи.
a b K
47

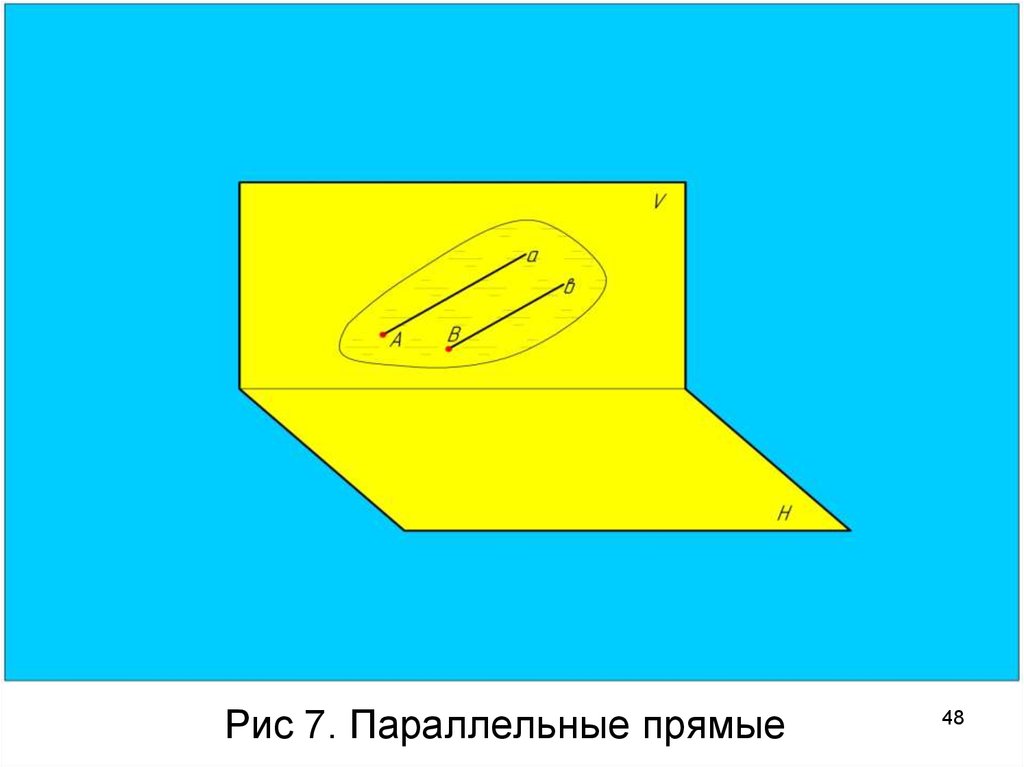
48. Рис 7. Параллельные прямые

48

49. Параллельные прямые

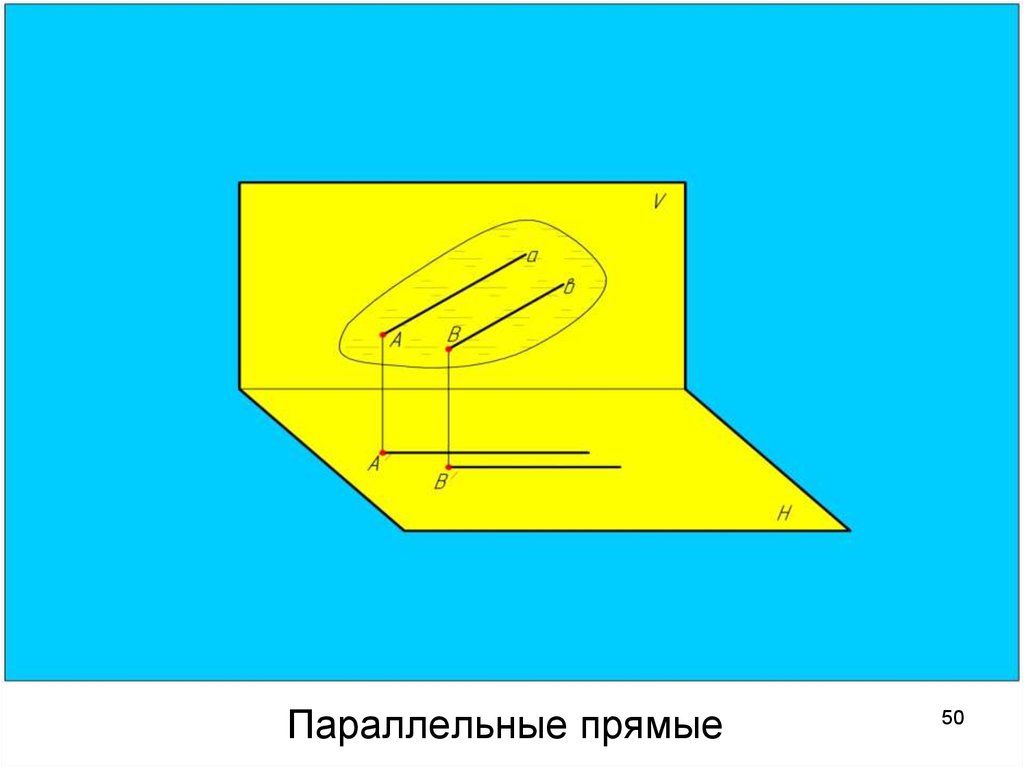
49

50. Параллельные прямые

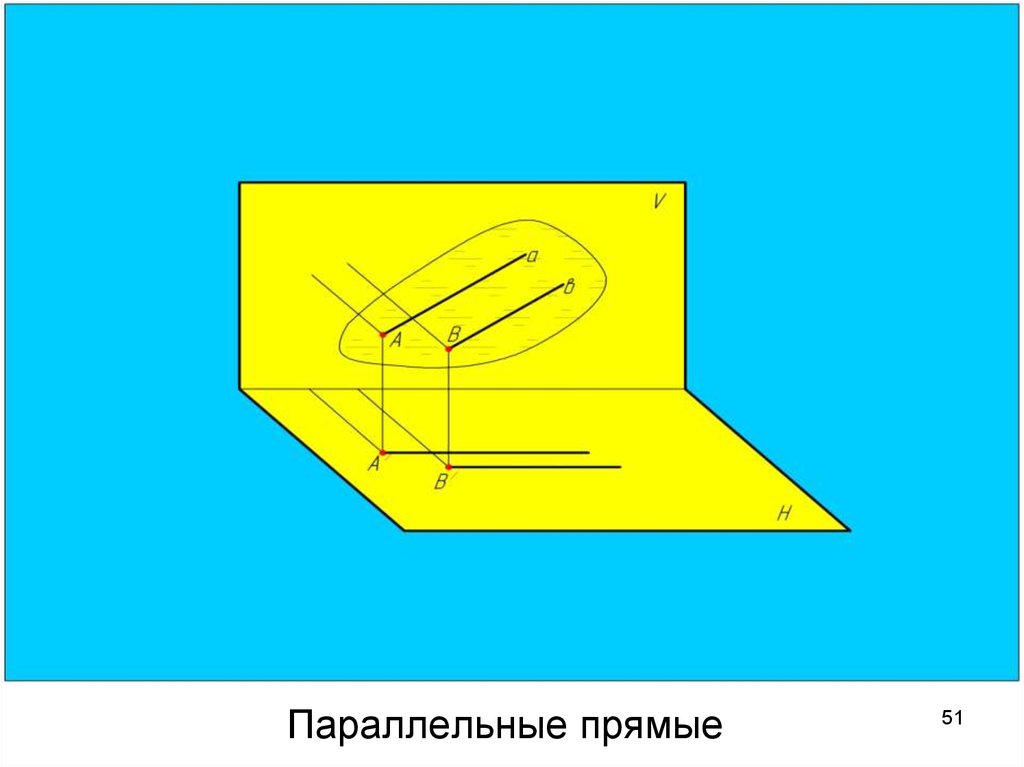
50

51. Параллельные прямые

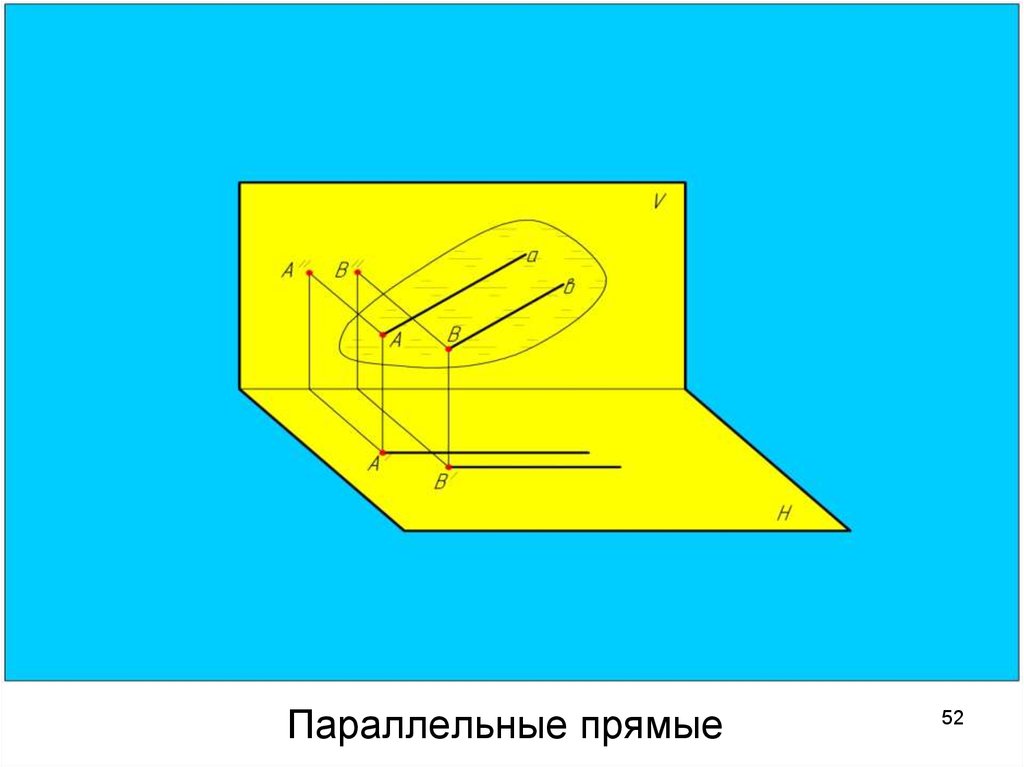
51

52. Параллельные прямые

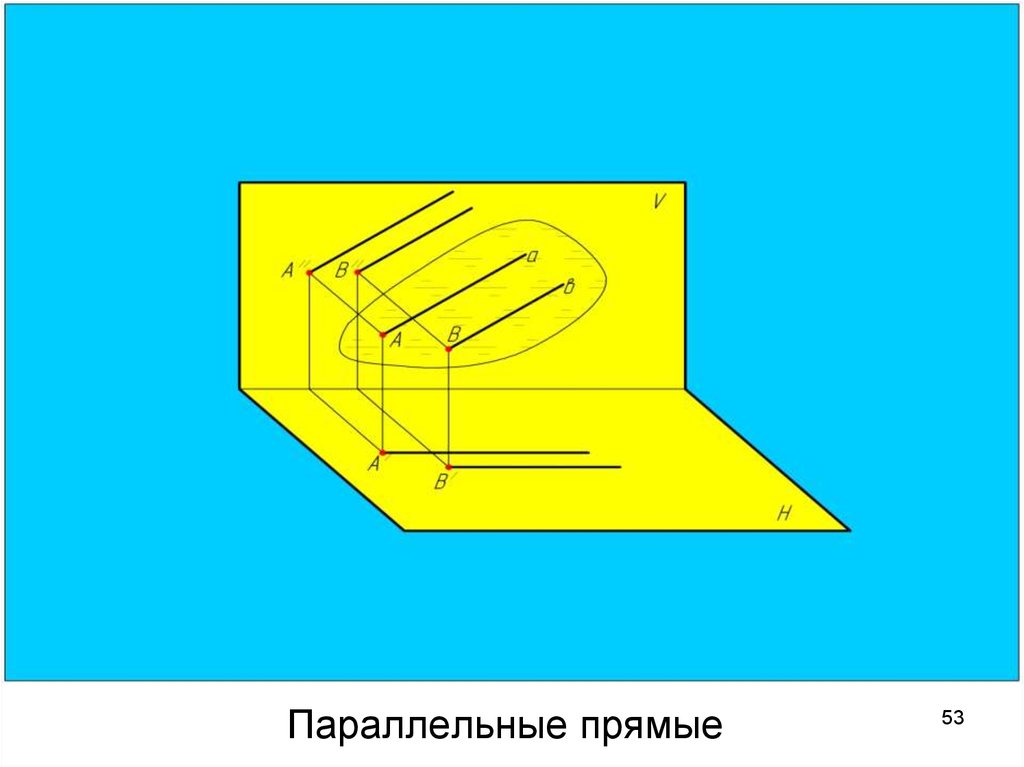
52

53. Параллельные прямые

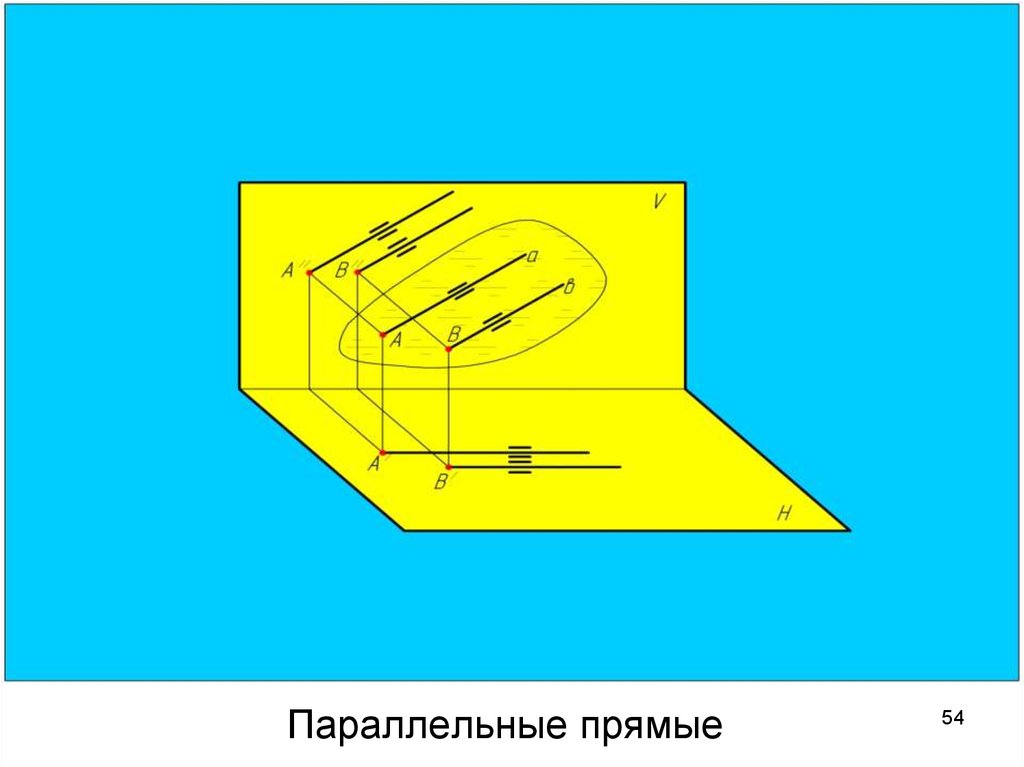
53

54. Параллельные прямые

54

55.

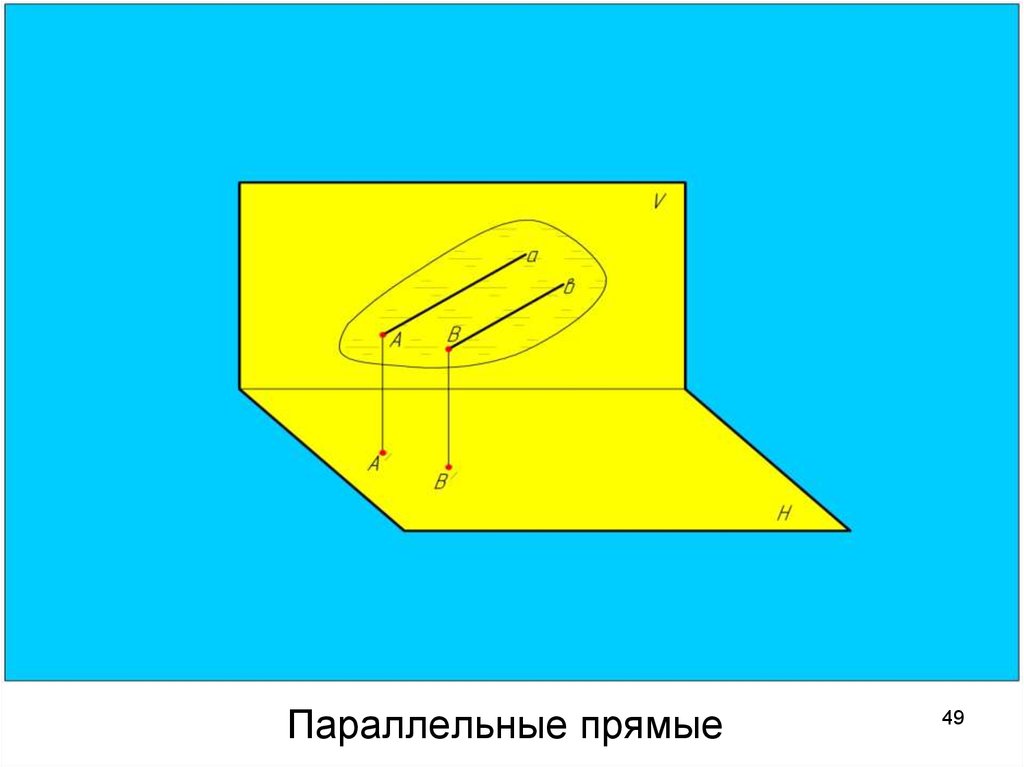
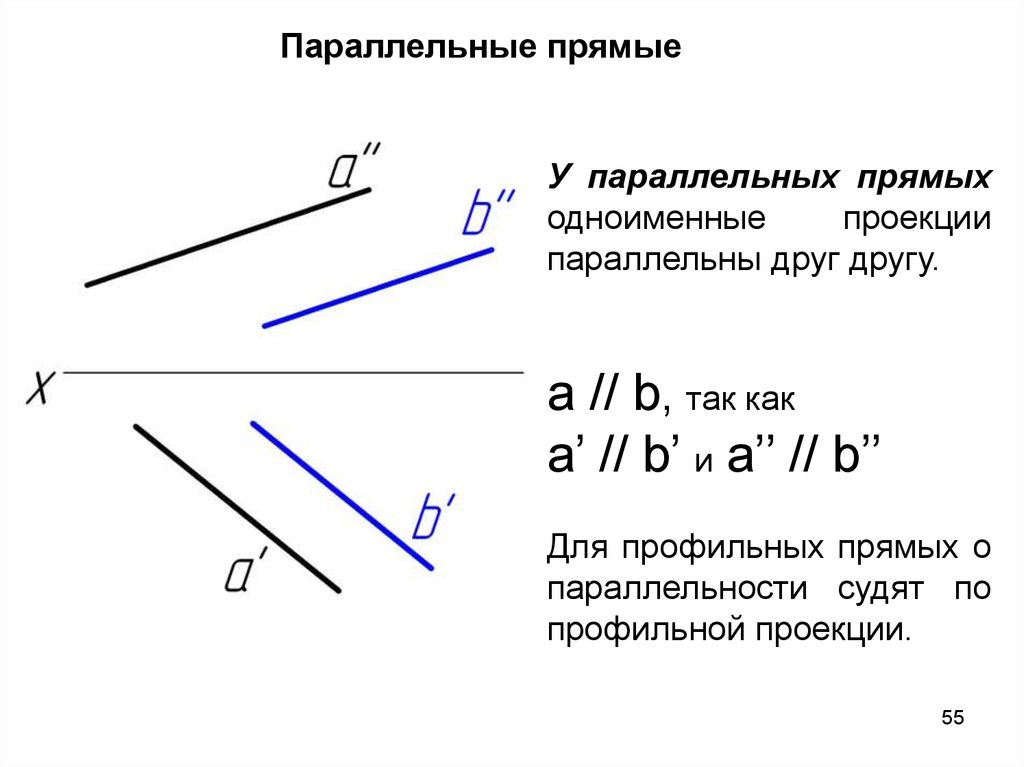
Параллельные прямые
У параллельных прямых
одноименные
проекции
параллельны друг другу.
a // b, так как
а’ // b’ и a’’ // b’’
Для профильных прямых о
параллельности судят по
профильной проекции.
55

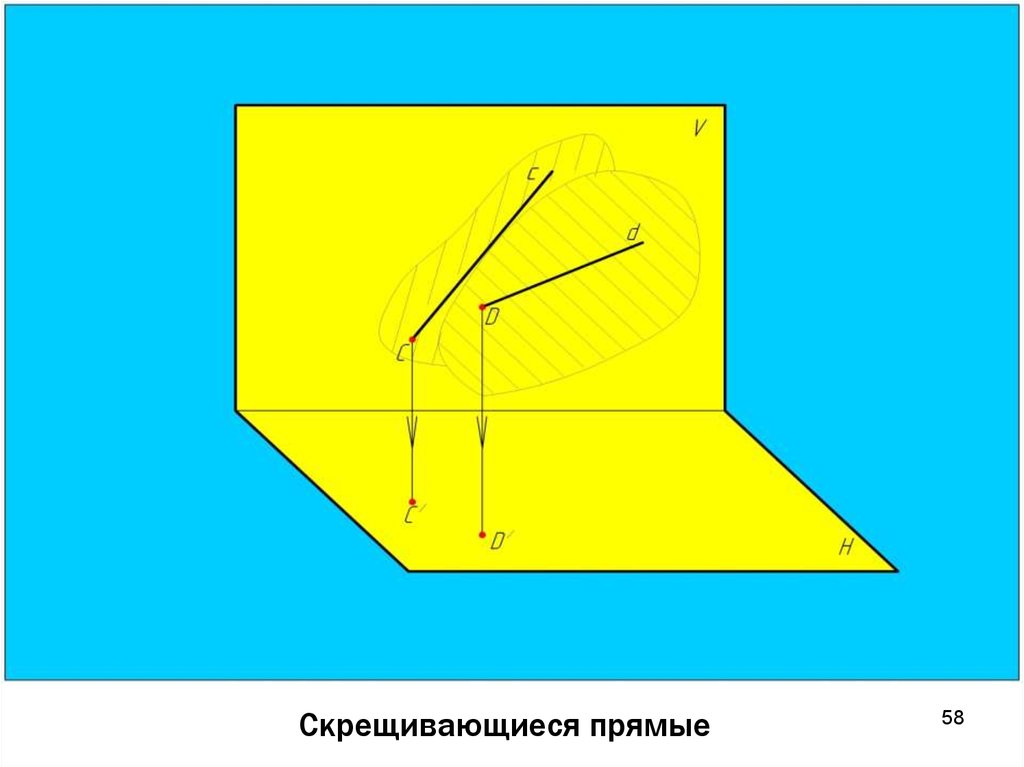
56. Скрещивающиеся прямые

56

57. Скрещивающиеся прямые

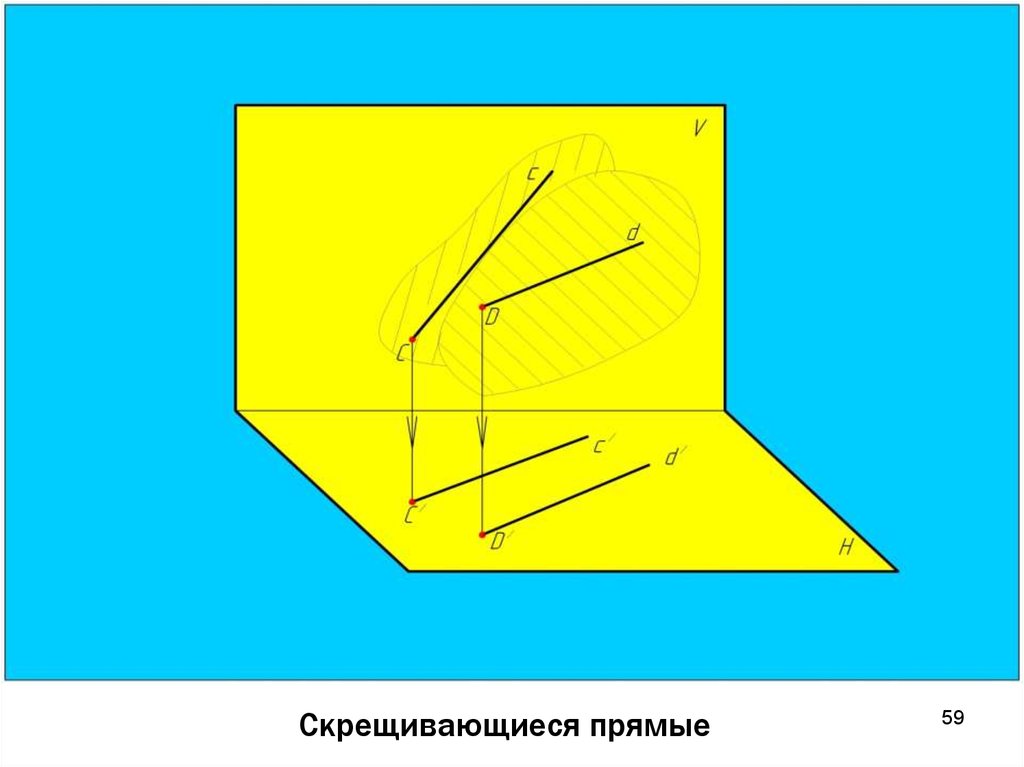
57

58. Скрещивающиеся прямые

58

59. Скрещивающиеся прямые

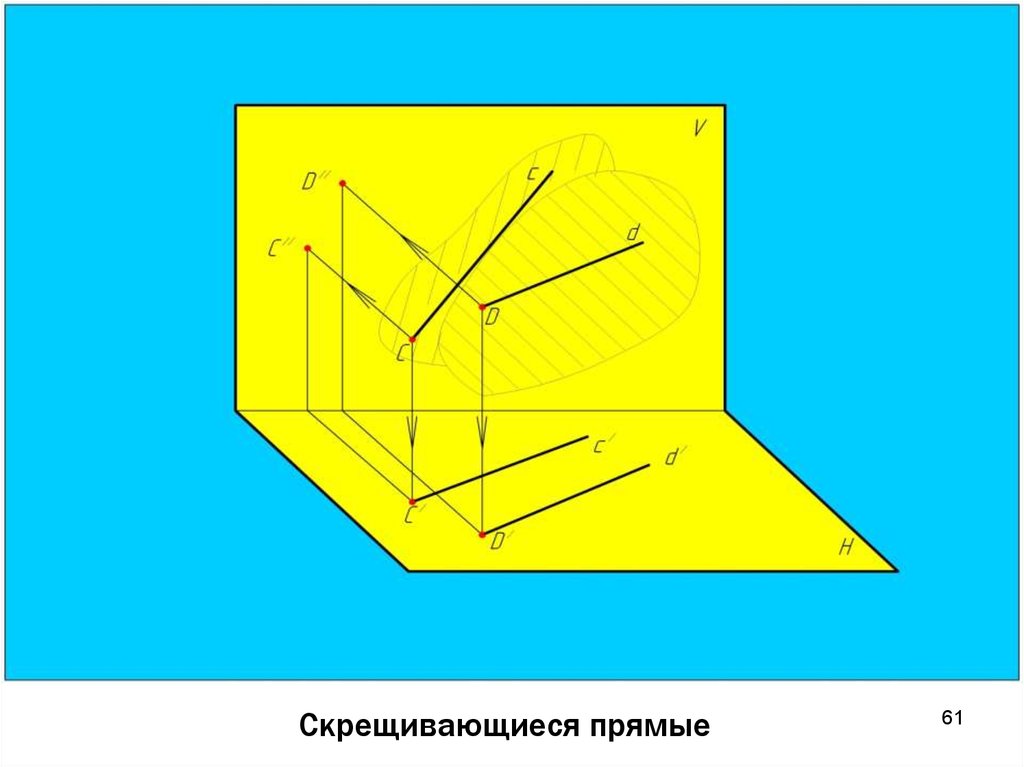
59

60. Скрещивающиеся прямые

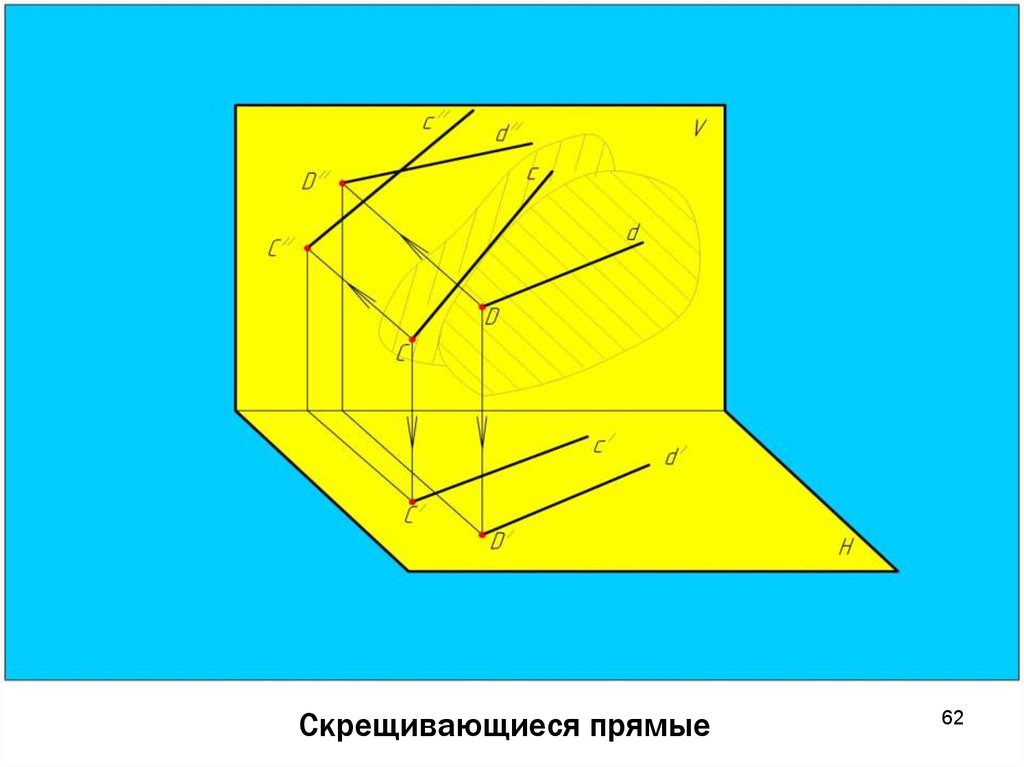
61

61. Скрещивающиеся прямые

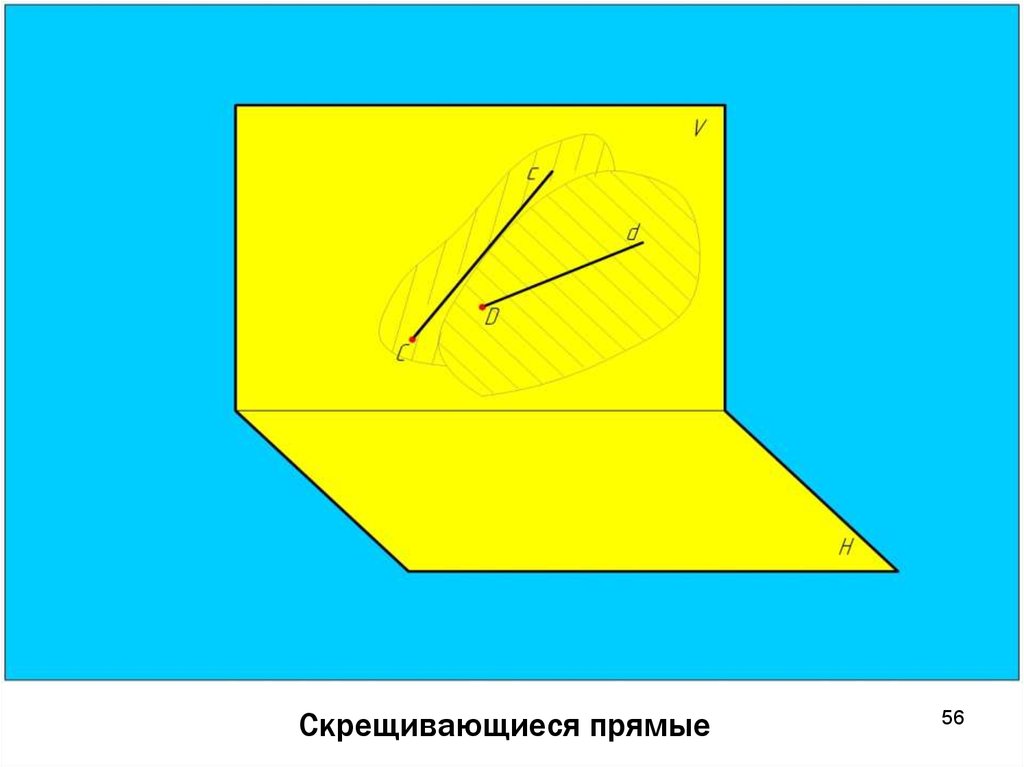
62

62. Скрещивающиеся прямые

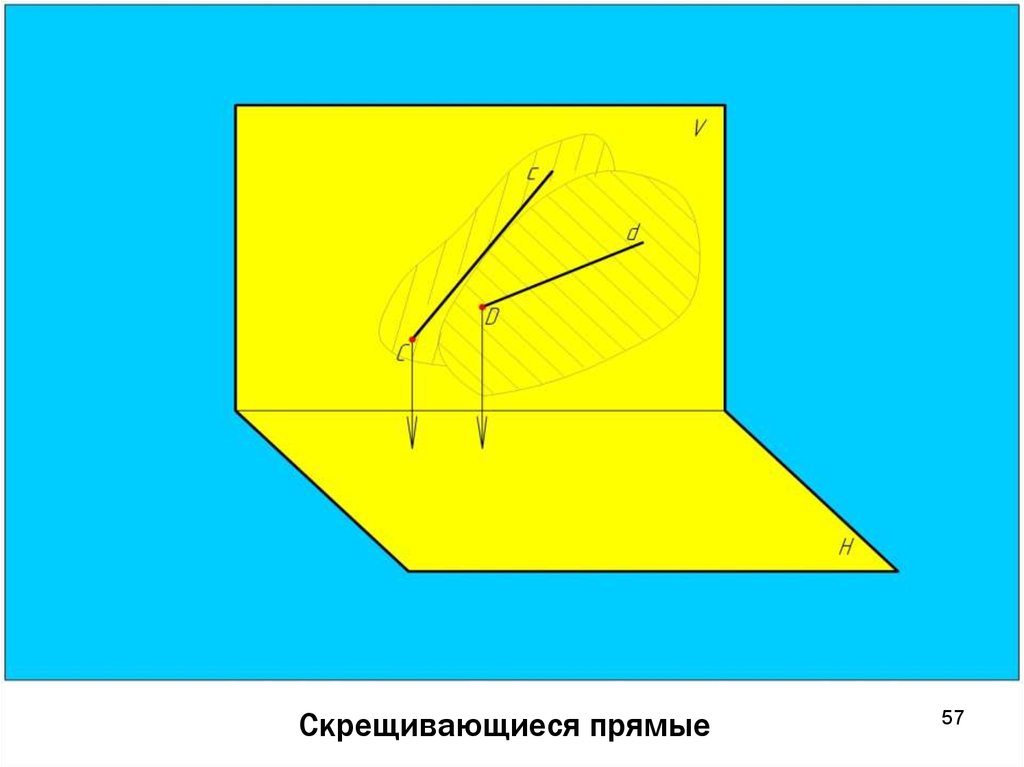
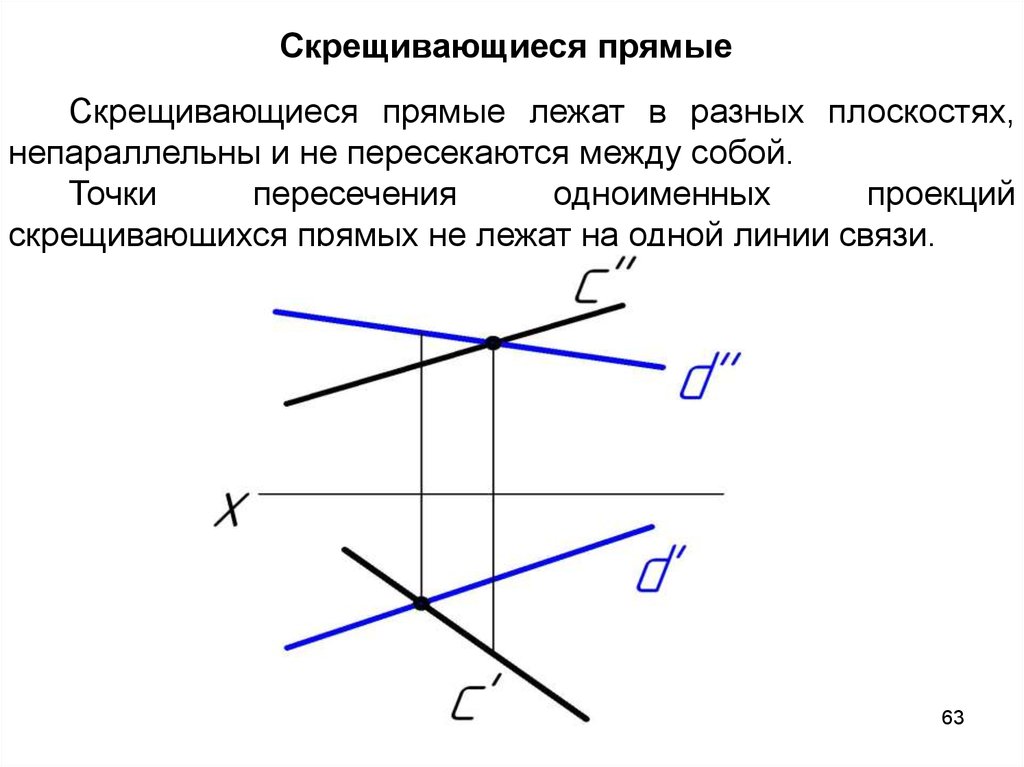
Скрещивающиеся прямые лежат в разных плоскостях,
непараллельны и не пересекаются между собой.
Точки
пересечения
одноименных
проекций
скрещивающихся прямых не лежат на одной линии связи.
63

63.

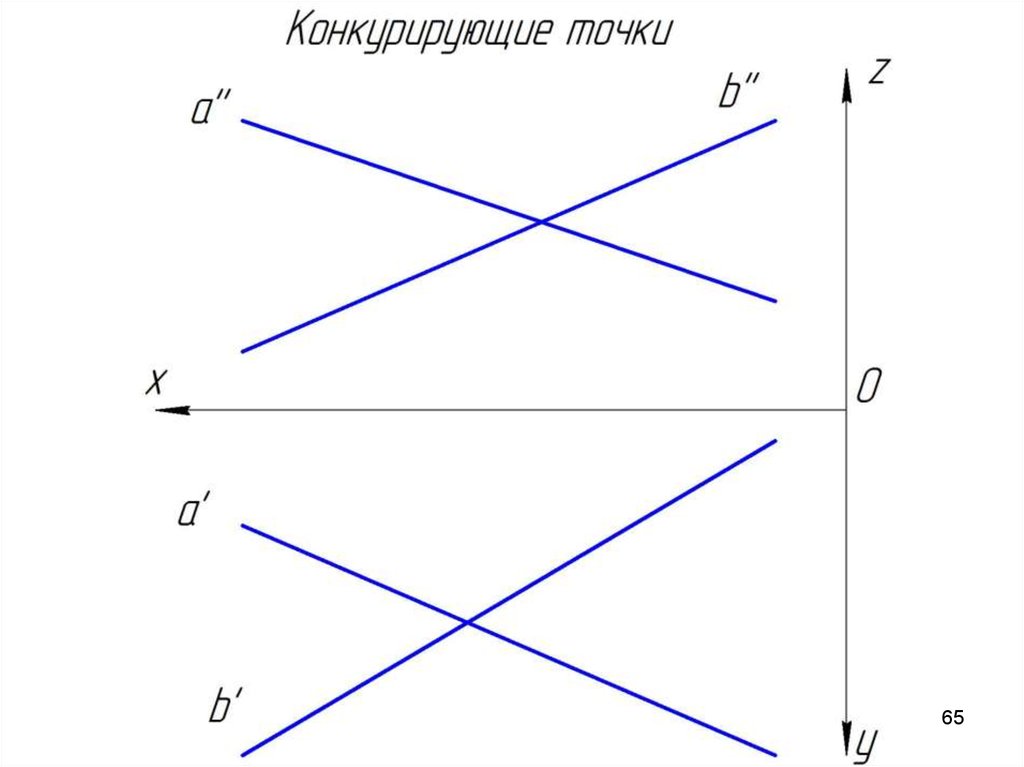
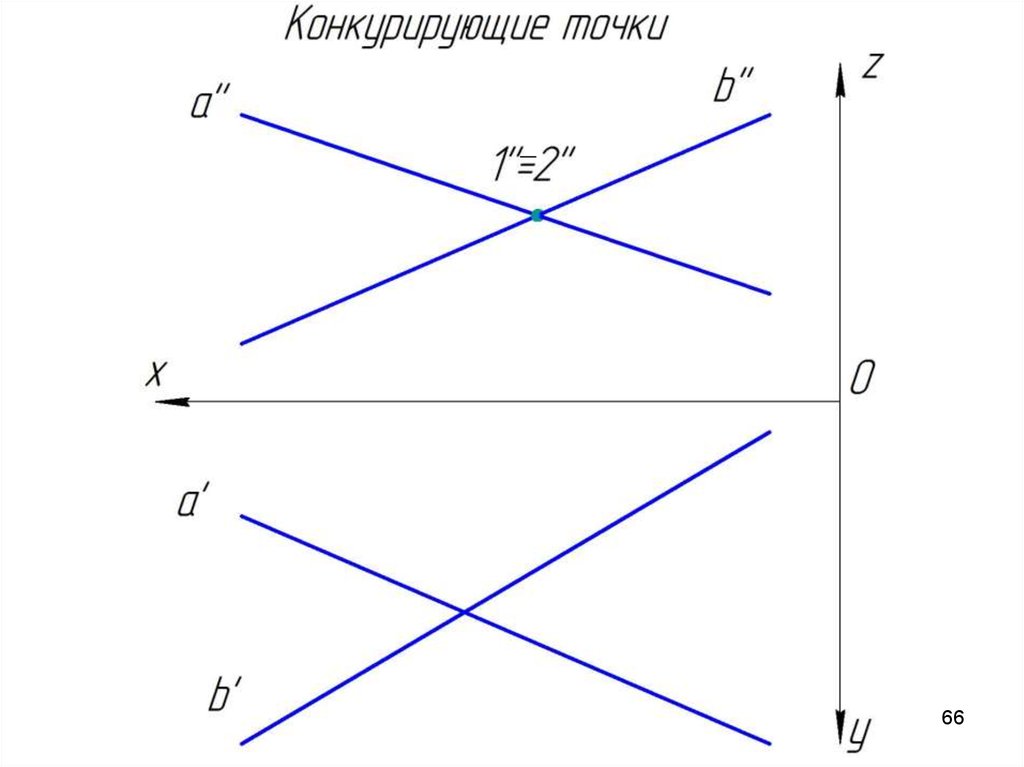
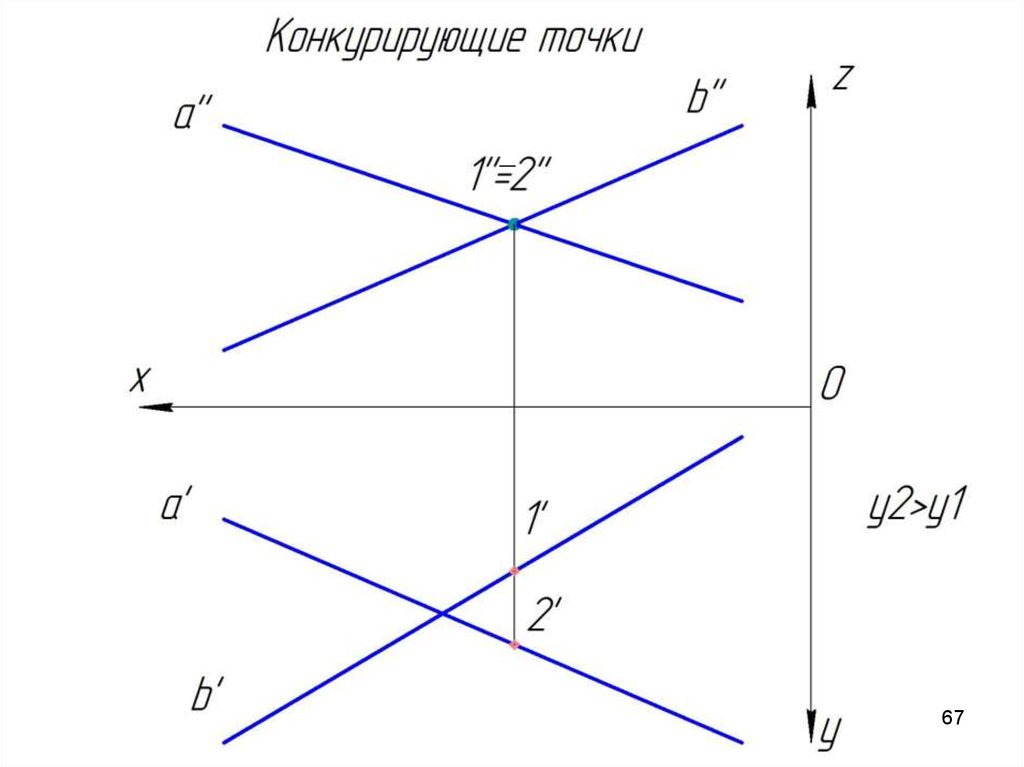
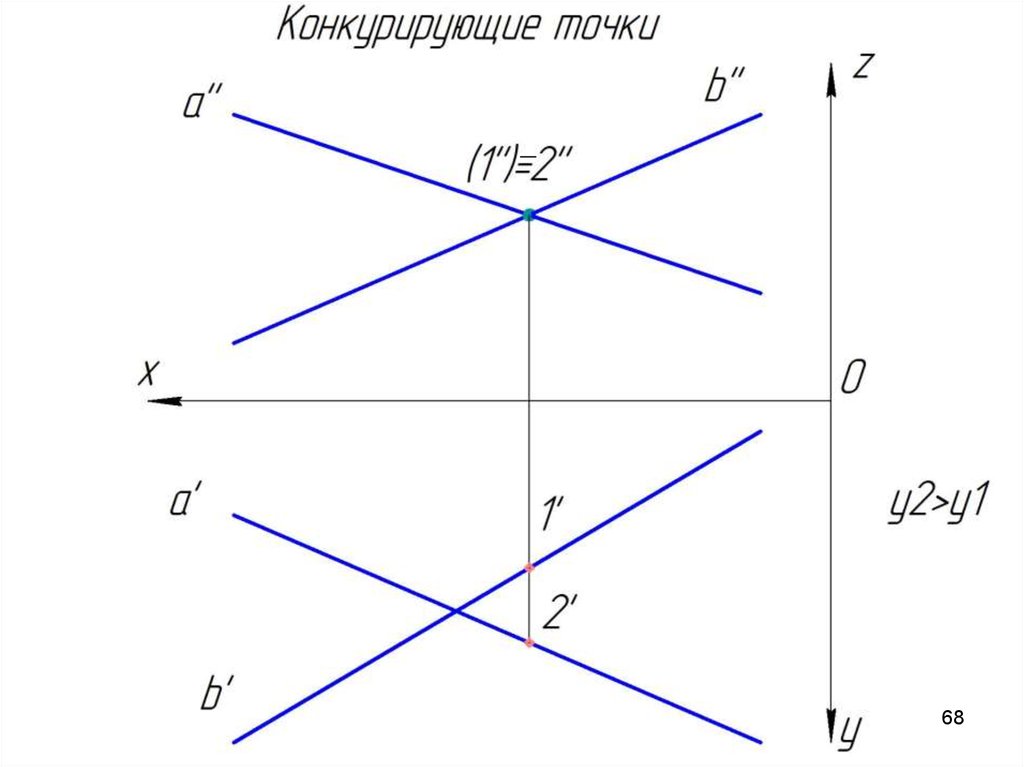
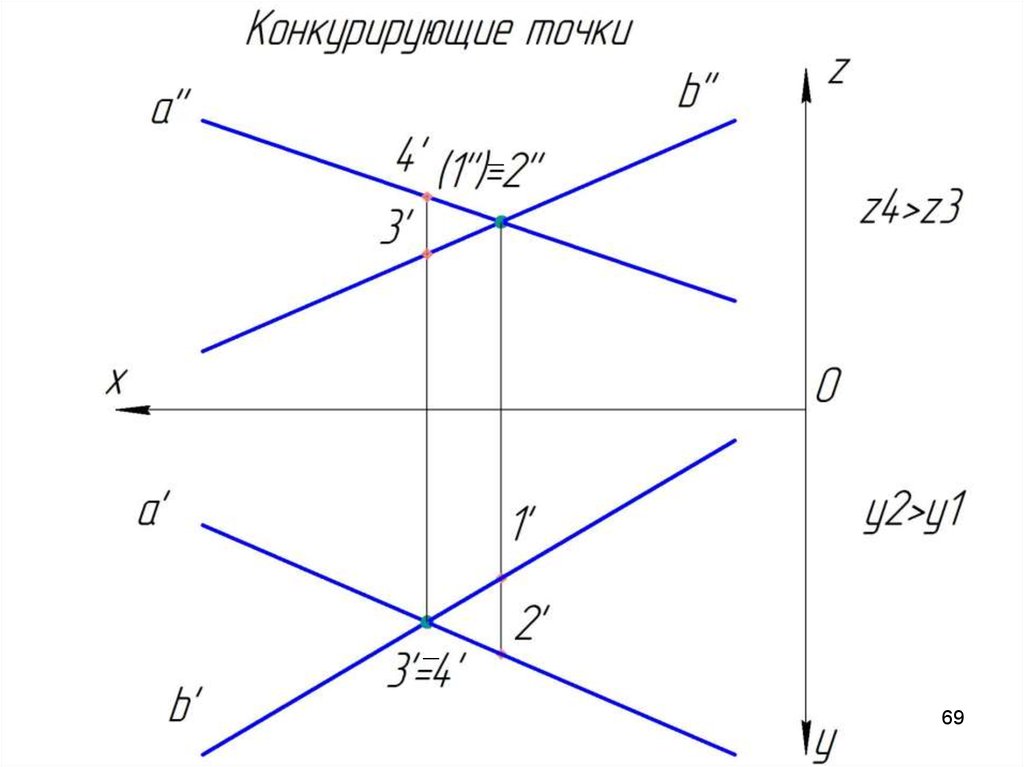
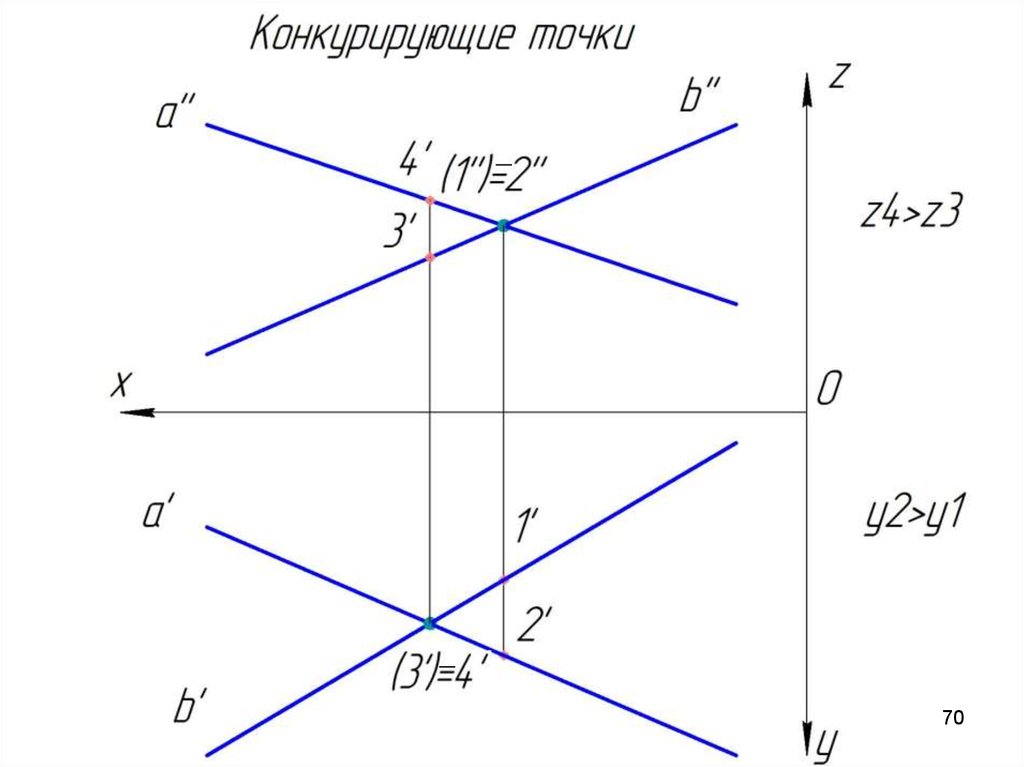
Конкурирующие точки
Точки, которые принадлежат разным прямым, но
проекции которых совпадают, называются конкурирующими.
С помощью конкурирующих точек определяется взаимная
видимость геометрических образов. Пусть заданы две
скрещивающихся прямые a и b. Определим какая проекция
какой прямой накладывается на другую.
64

64.

65

65.

66

66.

67

67.

68

68.

69

69.

70