Системы непрерывных случайных величин

1. Системы непрерывных случайных величин

Плотность распределения
P x X x x, y Y y y
f x, y x y o x y
1. f x, y 0
2.
f x, y dxdy 1
y+Δy
y
х
х+Δх
3. P X ,Y D f x, y dxdy
D
x, y
4. f x, y непрерывна f x, y Fxy
1

2. Системы непрерывных случайных величин

Функция распределения
F x , y P X x , Y y
Cвойства ф.р.
1. 0 F ( x, y) 1
F ( x, y )
x
y
f x, y dxdy
2. a b, c d F (a, c) F (b, d )
3. непрерывна
y
M(x,y)
х
2

3. Системы непрерывных случайных величин

Функция распределения
F x , y P X x , Y y
Cвойства ф.р.
1. 0 F ( x, y) 1
F ( x, y )
x
y
f x, y dxdy
2. a b, c d F (a, c) F (b, d )
3. непрерывна
4. F , y F x, 0
F , 0
5. F , 1
F , y FY y
F x, FX x
3

4. Системы непрерывных случайных величин

Условный закон распределения
f x, y
f x y
fY y
f x, y
f y x
f X x
fY y
f x, y dx
f X x
f x, y dy
Теорема (об умножении плотностей)
f x, y f X x f y x f Y y f x y
4

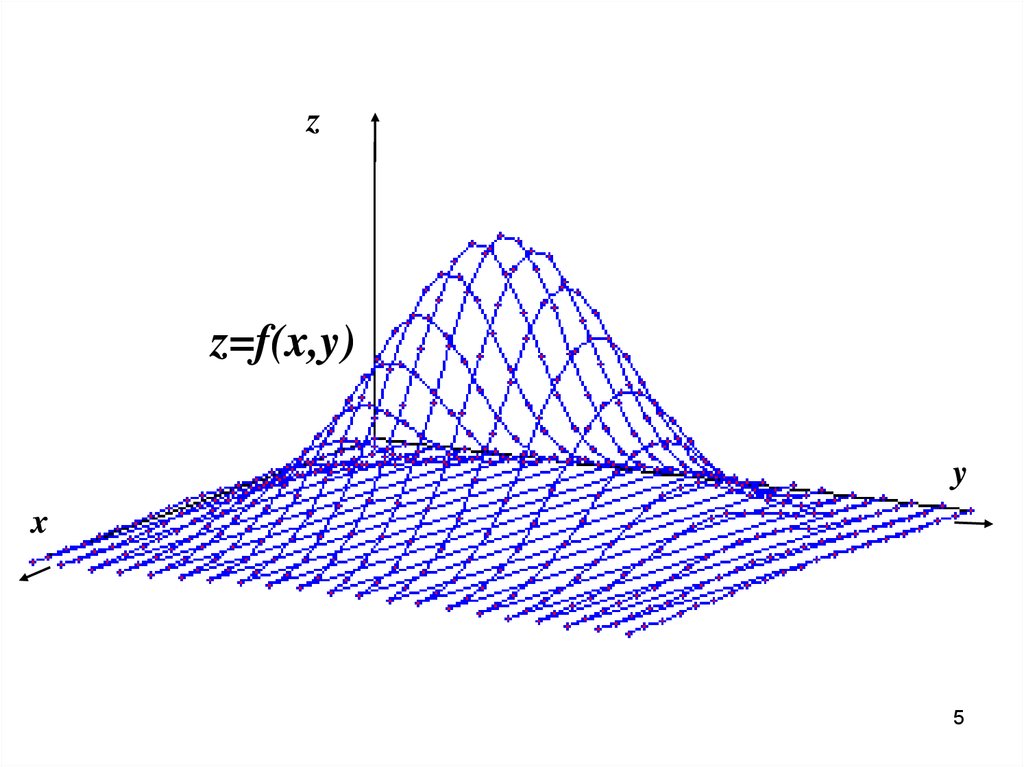
5.

z
z=f(x,y)
y
x
5

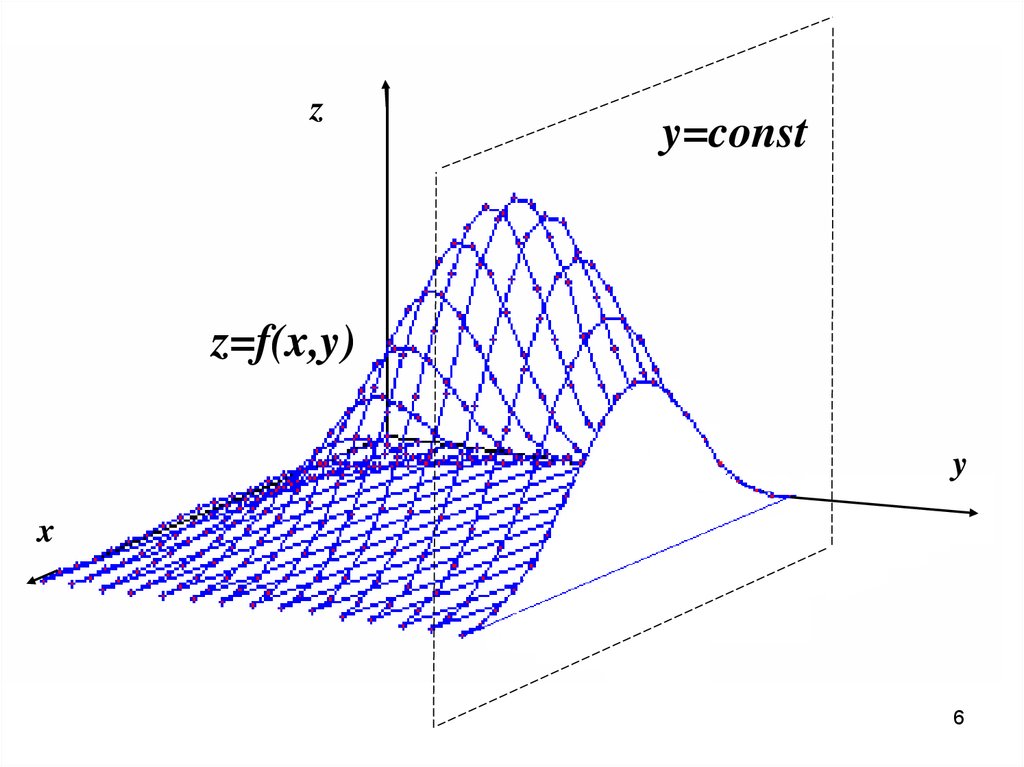
6.

z
y=const
z=f(x,y)
y
x
6

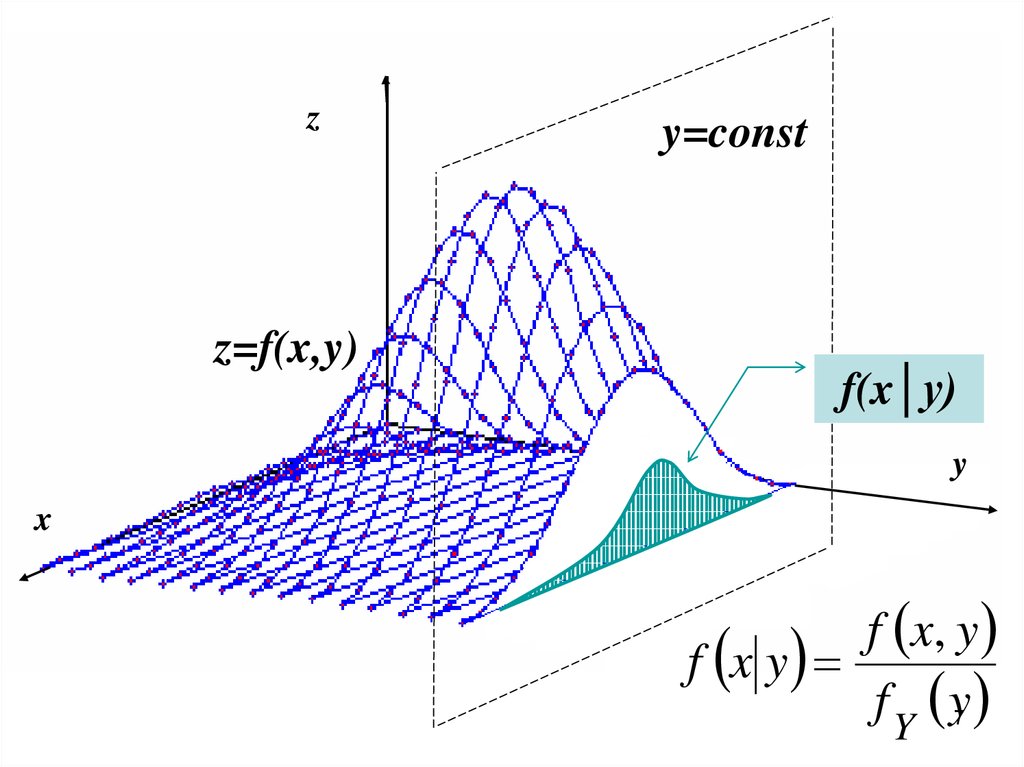
7.

z
y=const
z=f(x,y)
f(x│y)
y
x
f x, y
f x y
f Y y7

8. Системы непрерывных случайных величин

Теорема
(о независимости компонент системы НСВ)
Следующие условия независимости системы двух
НСВ эквивалентны:
A. F x, y F X x FY y
Б . f x, y f X x f Y y
B. f y x f Y y
Г . f x y f X x
8

9. Системы непрерывных случайных величин

Пример. Найти условную плотность
распределения f(y│x), если
y=x
2 x y ïðè 0 y x 1,
f x, y
0 ïðè îñòàëüíûõ x è y
x
1
f x, y
f
y
x
x
f X x
f X x f x, y dy 2 x y dy
Решение.
f y x
0
2 x y
3x
2
x
y
2
2 xy
3x
2 0
2
при 0 y 1
(x – произвольное фиксированное из [0;1])
9