Похожие презентации:
Предел функции в точке. Односторонние пределы. Пределы на бесконечности. Непрерывность функции. Точки разрыва функции
1.
Лекция N11Лектор: доц. Лаптева Надежда Александровна
Тема: Функция. Предел функции в точке.
Односторонние пределы. Пределы на
бесконечности. Непрерывность функции.
Точки разрыва функции и их
классификация.
2.
1. Предел в точке.Рассмотрим пример.
Построить график функции
x 1,
x 1 x 1,
y
x 1 не сущ., x 1.
2
3.
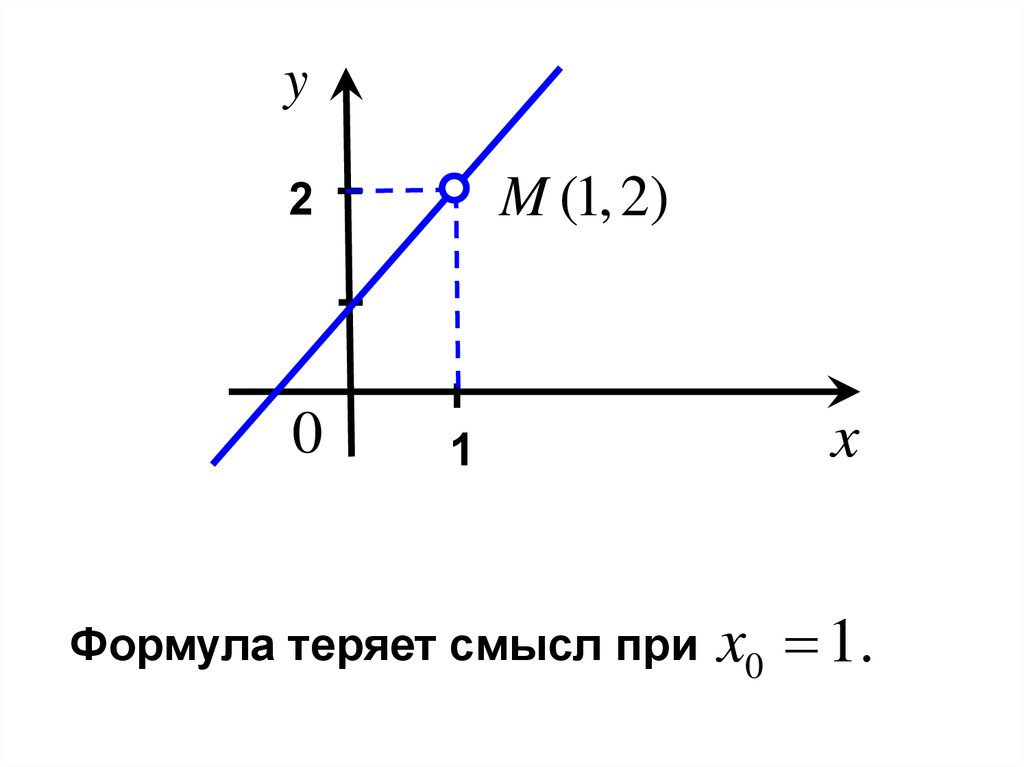
yM (1, 2)
2
0
1
Формула теряет смысл при
x
x0 1.
4.
В этом случае пишут:y ( x) 2
при
x 1.
По-другому:
lim y( x) 2.
x 1
5.
Способы вычисления предела1. Предел дроби при x :
деление на старшую степень.
0
1
2
2
2
1 2x
x
lim
lim
2.
2
x 2
x 2 x
1
2
x
0
Пример.
6.
2. Разложение на множители, когдаx
Пример.
x 1
x 1) 2.
lim
lim(
x 1
x 1 x 1
2
7.
Односторонние пределыВо многих случаях функция определена
только с одной стороны от x0 . Тогда
предел называют пределом слева, или
пределом справа.
2
y1
Пример 1.
lim ln x .
x 0
0
-1
-2
-3
1
x
8.
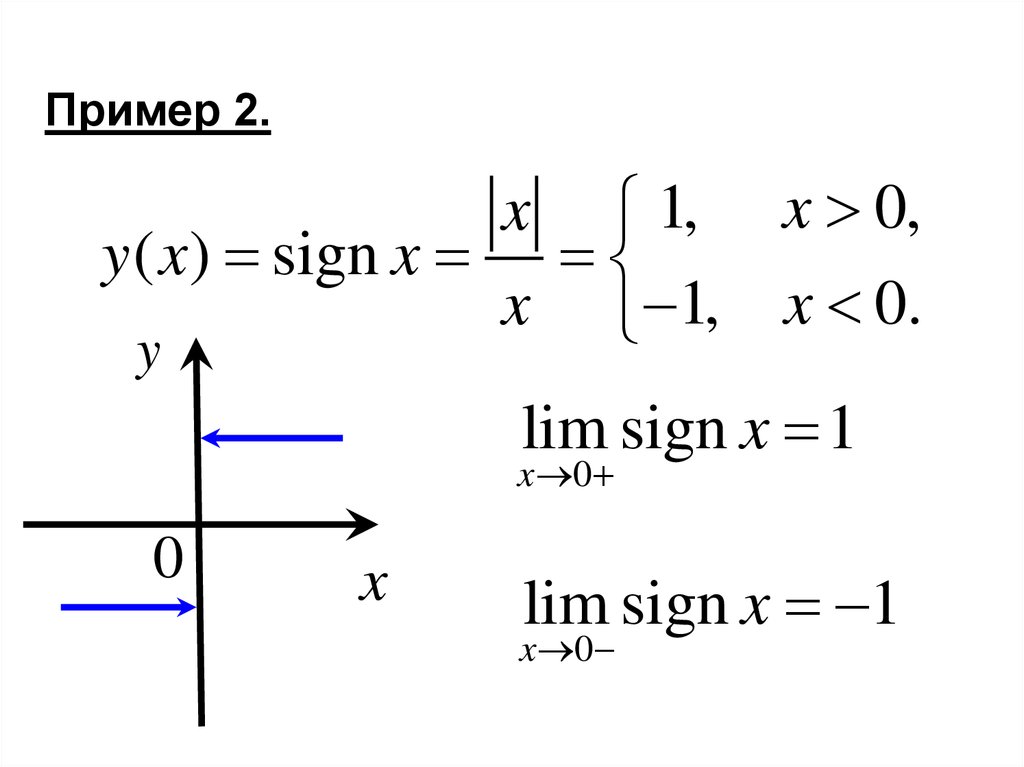
Пример 2.x 1, x 0,
y ( x) sign x
x 1, x 0.
y
lim sign x 1
x 0
0
x
lim sign x 1
x 0
9.
Опр. Функция y y ( x) называетсянепрерывной в точке x0 , если
lim y( x) y( x0 ).
x x0
Все элементарные функции
непрерывны на своей области
определения.
Пример. y x , y e
- непрерывные функции.
2
x
,
y sin x
10.
Опр. Если в точке x0 функция неявляется непрерывной, то x0 - точка
разрыва.
Рассматриваются точки разрыва 1-го
и 2-ого рода.
11.
Пример.y( x) sign x.
y
0
x0 0
- точка разрыва
1-го рода (конечный разрыв).
x
12.
Пример.1
y ( x) .
x
x0 0
y
- точка
разрыва 2-ого рода
(бесконечный разрыв).
1
lim ;
x 0 x
0
1
lim .
x 0 x
x
13.
Тема: Производная функции, правилавычисления.
Производная сложной функции.
Производные высших порядков.
Дифференциал функции.
14.
Приращение аргументаи приращение функции
Пусть дана функция y f ( x).
Рассмотрим два значения её
аргумента: исходное x0 и новое x.
Разность x x0 называется
приращением аргумента x в точке
и обозначается символом x.
x0
15.
y y0 f ( x) f ( x0 ) называетсяприращением функции и обозначается y.
Опр. Производной функции в точке
называется
x0
f ( x0 x) f ( x0 )
f ( x0 ) lim
.
x 0
x
16.
Пример. Найти производную2
функции y x .
y :
2
2
2
y ( x x) x 2 x x ( x) .
2
y
2 x x ( x)
y lim
lim
x 0 x
x 0
x
lim(2 x x) 2 x.
Найдем
x 0
Таким образом
( x ) 2 x.
2
17.
Эта производная определена на всейчисловой оси, так как при её нахождении
значение x было выбрано произвольно.
Опр. Функция y f ( x), имеющая
производную в точке x0 , называется
дифференцируемой в этой точке.
Функция y f ( x) называется
дифференцируемой в интервале ( a, b),
если она дифференцируема в каждой
точке этого интервала.
18.
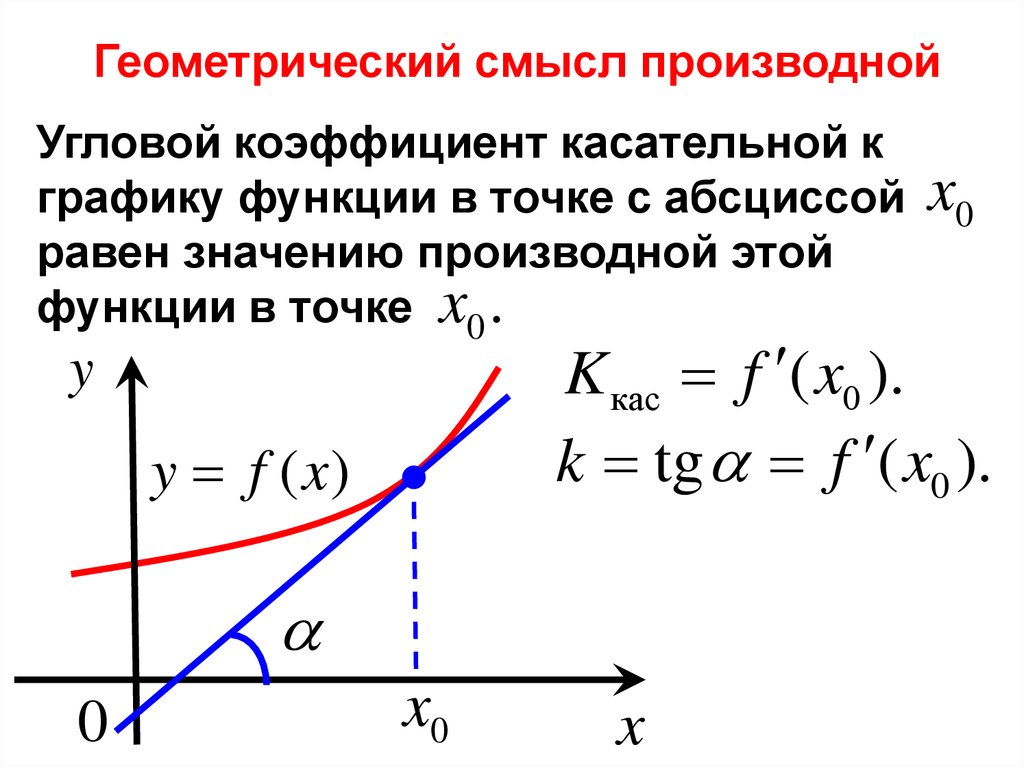
Геометрический смысл производнойУгловой коэффициент касательной к
графику функции в точке с абсциссой
равен значению производной этой
функции в точке x0 .
K кас f ( x0 ).
k tg f ( x0 ).
y
y f ( x)
0
x0
x0
x
19.
Функция y x не имеет производной вточке x 0, т.к. график функции y x
в точке O(0,0) не имеет касательной.
y
0
x
20.
Таблица производных (степени)1. const 0.
1
2. x x .
3.
a a
x
x
x
ln a; e e .
4. log a x
x
1
;
x ln a
1
ln x .
x
21.
Таблица производных(тригонометрия)
5. sin x cos x.
6. cos x sin x.
1
7. tg x
.
2
cos x
1
8. ctg x 2 .
sin x
22.
Таблица производных(arc-тригонометрия)
9. arcsin x
1
.
1 x
1
10. arccos x
.
2
1 x
1
11. arctg x
.
2
1 x
1
12. arcctg x
.
2
1 x
2
23.
Основные правила дифференцированияЕсли функции u u ( x) и v v( x)
дифференцируемы в данной точке x,
то в этой точке дифференцируемы и
их сумма и произведение, причем
u v u v ,
u v u v v u.
24.
Если функции u u ( x) и v v( x)дифференцируемы в данной точке x
и v( x) 0, то в той же точке
дифференцируемо и их частное,
причем
u u v v u
.
2
v
v
25.
Примеры.1)
y x sin x.
2
Найти
y .
2
y x sin x x sin x
2
2 x sin x x cos x,
2
26.
xe
2)
Найти y (1).
y .
x
x
x
x
e x e
e ( x 1)
y
;
2
2
x
x
e (1 1)
y (1)
0, y (1) 0.
1
27.
Производная сложной функцииПусть y f (u ) и u ( x).
Тогда y есть сложная функция x :
Теорема
y f ( x) .
y x yu u x .
28.
Примерыy sin 2 x.
y cos 2 x (2 x)' 2cos 2 x.
2
2) y cos x.
2
Запишем y cos x :
y 2cos x cos x
1)
2cos x sin x sin 2 x.
29.
Производные высших порядковПусть функция y f ( x)
дифференцируема в некотором
интервале.
Тогда её производная f ( x )
является функцией от x. Пусть эта
функция также имеет производную.
Эта производная называется второй
производной и обозначается
y f ( x) .
30.
Аналогично,y
(n)
y y
y
( n 1)
и т.д.:
.
Производные порядка выше первого
называются производными высшего
порядка.
31.
Примеры.1) Найти производную третьего
2x
порядка от функции y e .
y e ; y 2e ; y 4e ; y 8e .
(3)
y
ln
x
.
2)
Найти y .
1
1
2
3
y x ; y x ; y 2 x .
x
2x
2x
2x
2x
32.
Дифференциал функцииРассмотрим функцию
Найдем y.
y x .
3
y x x x
3
3
x 3x x 3 x x x x
3
2
2
3
3
3x x 3x x x .
2
2
33.
Приращение функции можнорассматривать как сумму двух слагаемых:
3x x
2
- линейное относительно
3x x x
2
- нелинейное
относительно
x;
x.
34.
При x 0 оба слагаемых стремятся кнулю, но второе слагаемое быстрее
стремится к нулю. Поэтому при малых x
2
считают, что y 3x x (т.е. считают,
что y приближенно равно линейной
части). Эту часть называют главной
частью приращения функции или
дифференциалом.
Дифференциал функции y
обозначают dy.
f ( x)
35.
Теорема. Если функция y f ( x) имеетв точке x дифференциал, то она имеет в
этой точке производную и наоборот, если
функция y f ( x) имеет в точке x
производную, то она имеет в этой точке
дифференциал.
Выражение для дифференциала
записывается в форме
dy f ( x) dx.
36.
Примеры.Найти дифференциалы функций
1)
2)
y sin x. dy cos x dx.
y e .
3x
dy e
3x
dx
dy 3e dx.
3x
37.
Связь между дифференцируемостьюи непрерывностью функции
Теорема. Если функция y f ( x)
дифференцируема в точке x0 , то она
в этой точке непрерывна.
Обратная теорема неверна: существуют
непрерывные функции, которые в
некоторых точках не являются
дифференцируемыми.
38.
Пример.y
y x.
0
x
В точке x 0 функция
непрерывна, так как
f ( x) x
lim f ( x) lim x .
x 0
x 0
39.
x x, поэтомуy
lim
1.
x 0 x
Справа от нуля
Слева от нуля
x x, поэтому
y
lim
1.
x 0 x
40.
Таким образом, отношениеx 0
y
x
при
справа и слева имеет различные
пределы, а это значит, что при x 0
это отношение предела не имеет, т.е.
производная f ( x ) в точке x 0
не существует.
























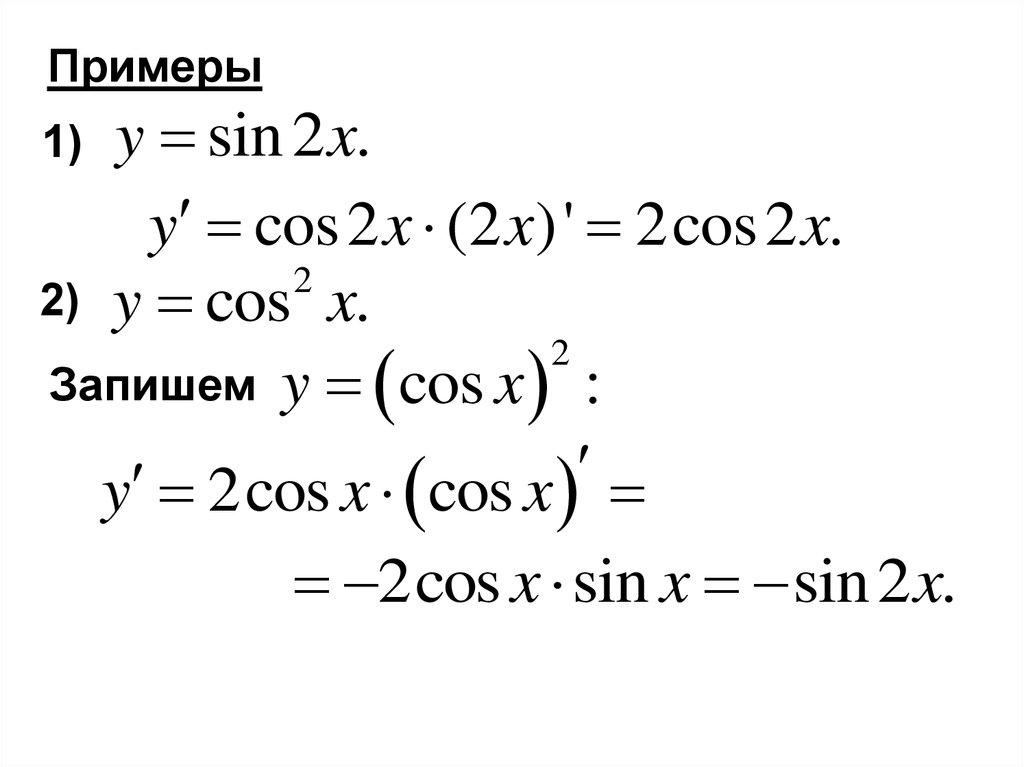












 Математика
Математика








