Похожие презентации:
Розв’язування тригонометричних рівнянь
1.
Математиканастільки серйозний
предмет, що не треба
пропускати
можливості зробити
його цікавішим.
Блез Паскаль
1623-1662
2. Розв’язування тригонометричних рівнянь
Урок-презентаціяРозв’язування
тригонометричних
рівнянь
3. Бліц-опитування
1. При якому значенні а тригонометричні рівнянняsinx=a i cosx=a мають розв’язки?
2. За якою формулою знаходимо розв’язок
тригонометричного рівняння cosx=a при │а│ ≤ 1.
3. Чому дорівнює розв’язок рівняння cosx=0?
4. Чому дорівнює розв’язок рівняння cosx=1?
5. Чому дорівнює розв’язок рівняння cosx=-1?
6. Чому дорівнює arccos(-a)?
4. Бліц-опитування
7. За якою формулою знаходимо розв’язоктригонометричного рівняння sinx=a при │а│ ≤ 1.
8. Чому дорівнює розв’язок рівняння sinx=0?
9. Чому дорівнює розв’язок рівняння sinx=1?
10. Чому дорівнює розв’язок рівняння sinx=-1?
11. Чому дорівнює arcsin(-a)?
5. Бліц-опитування
12. За якою формулою знаходимо розв’язок рівнянняtgx=a?
13. За якою формулою знаходимо розв’язок рівняння
ctgx=a?
14. Чому дорівнює arctg(-a)?
15. Чому дорівнює arcctg(-a)?
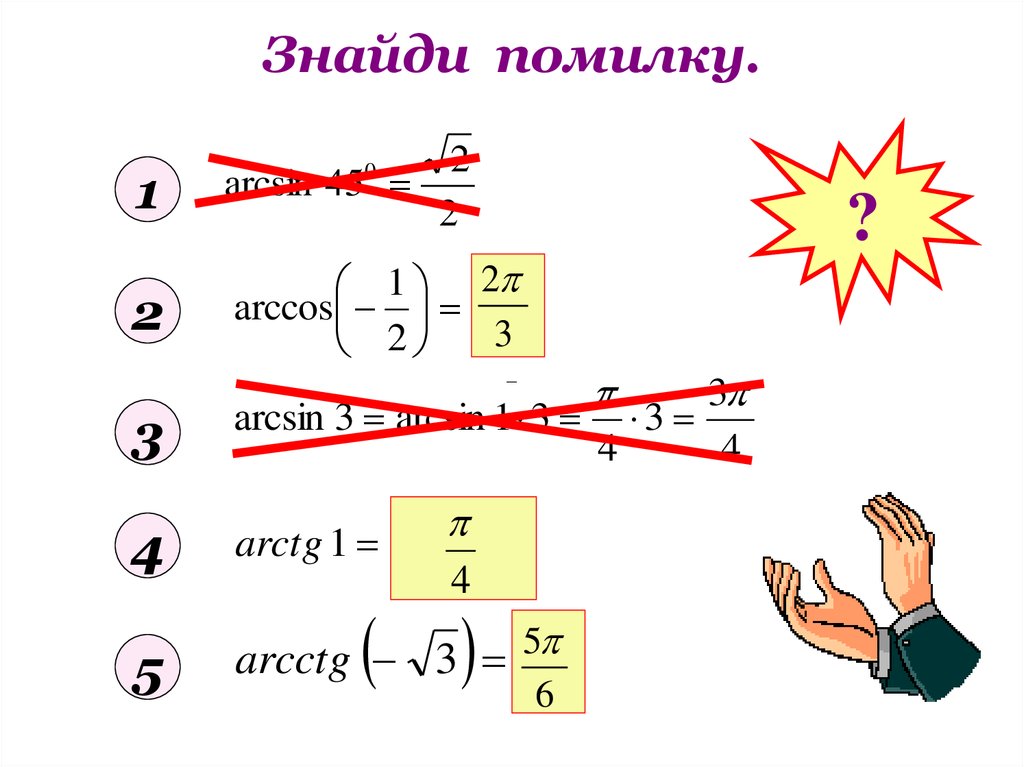
6. Знайди помилку.
12
arcsin 45
2
2
1 2
arccos
33
2
0
?
3
3
arcsin 3 arcsin 1 3 3
4
4
4
arctg 1 arctg
4 4
5
5
arcctg 3
66
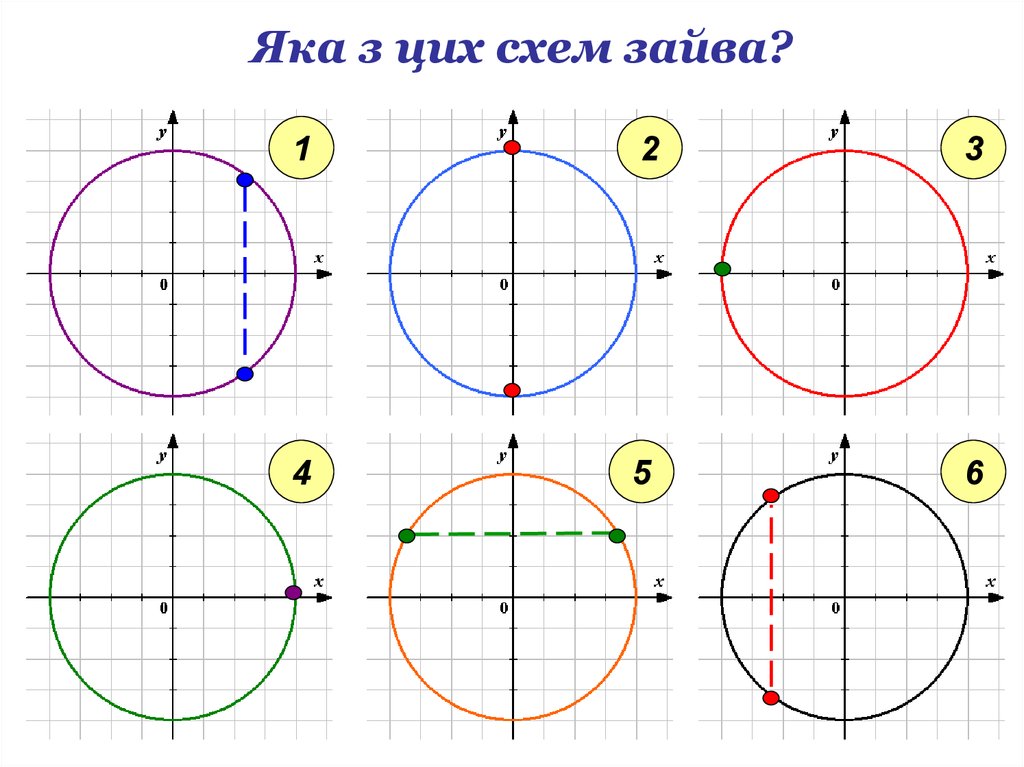
7. Яка з цих схем зайва?
12
3
4
5
6
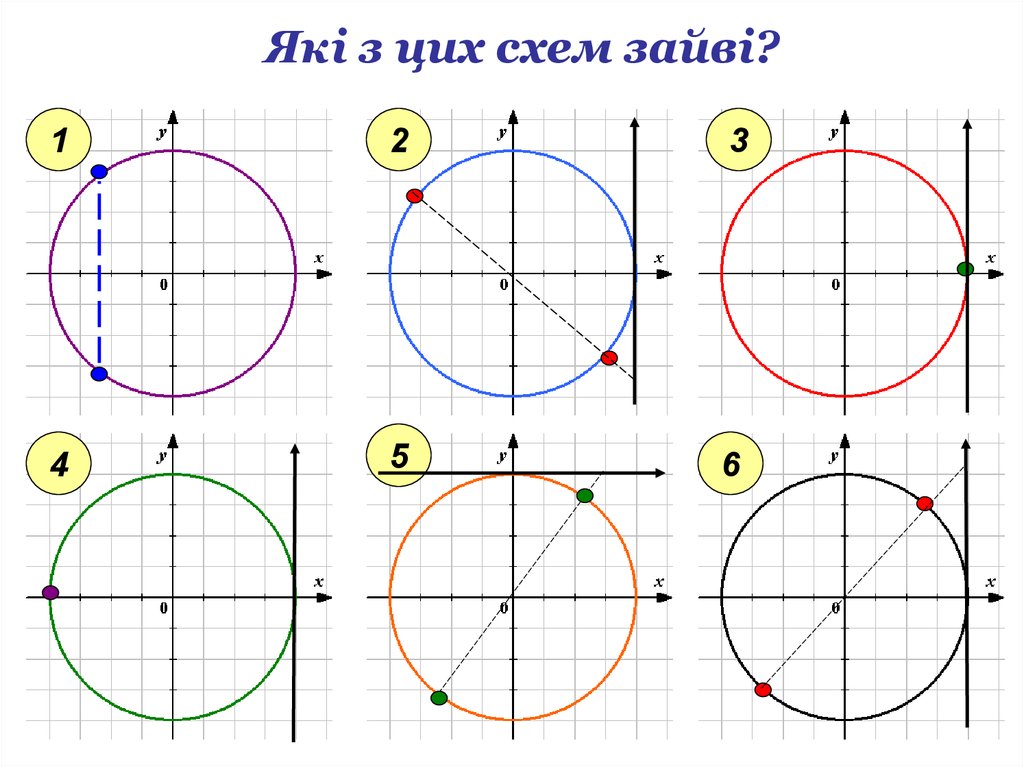
8. Які з цих схем зайві?
12
3
4
5
6
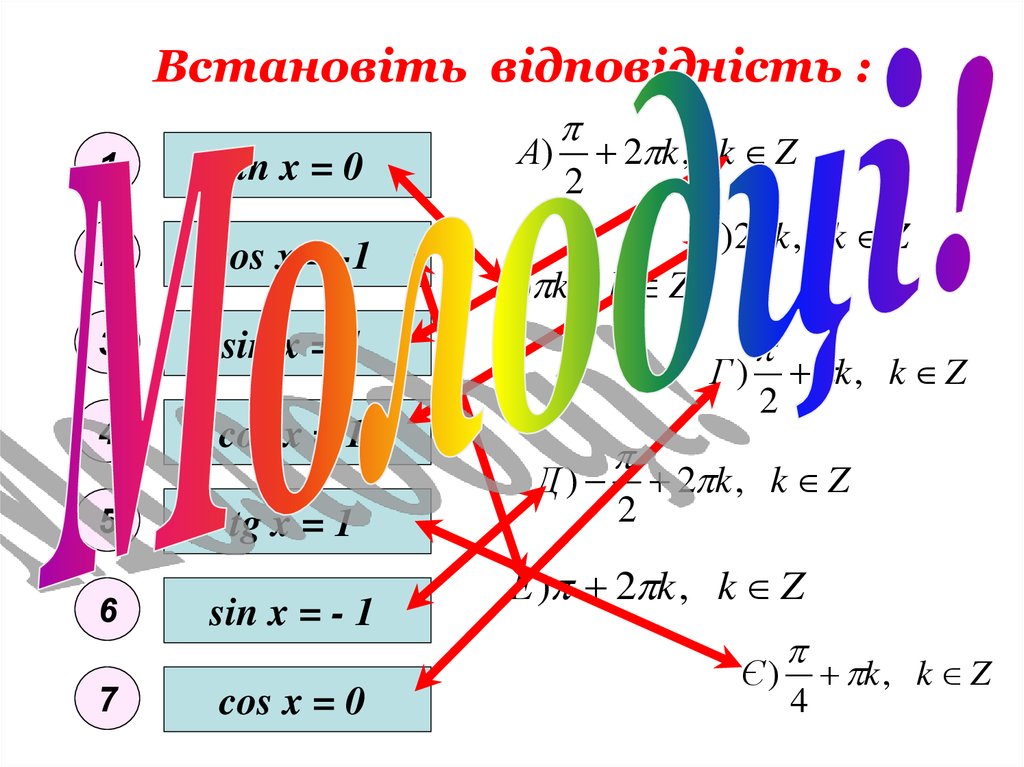
9. Встановіть відповідність:
1sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = - 1
cos x = 0
А)
2
2 k , k Z
Б )2 k , k Z
В ) k , k Z
Г)
Д)
2
2
k , k Z
2 k , k Z
Е ) 2 k , k Z
Є)
4
k , k Z
10. Встановіть відповідність :
1sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = - 1
cos x = 0
А)
2
2 k , k Z
Б )2 k , k Z
В ) k , k Z
Г)
Д)
2
2
k , k Z
2 k , k Z
Е ) 2 k , k Z
Є)
4
k , k Z
11. Методи розв’язування тригонометричних рівнянь.
Рівняння, яке зводитьсядо квадратного
2 sin x cos x 1 0
2
12. Методи розв’язування тригонометричних рівнянь.
Рівняння, яке зводитьсядо квадратного
Розкладання на множники
tg x 3tgx 0
2
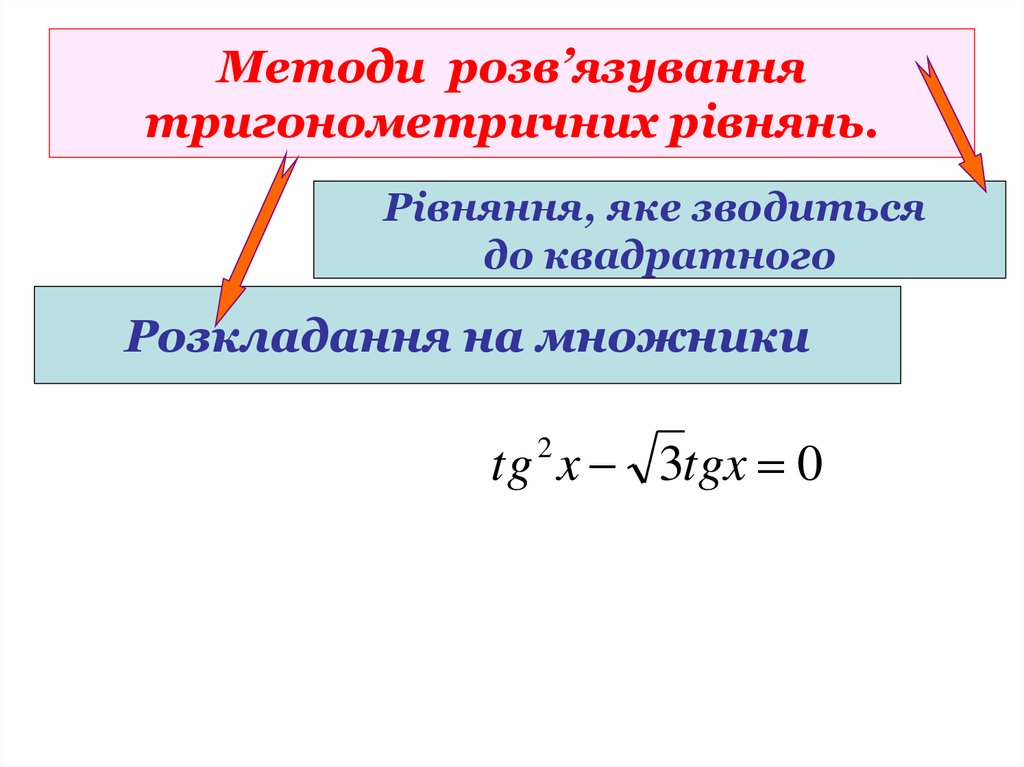
13. Методи розв’язування тригонометричних рівнянь.
Рівняння, яке зводитьсядо квадратного
Розкладання на множники
Однорідне І степеня
2 cos 2x 3sin 2x 0
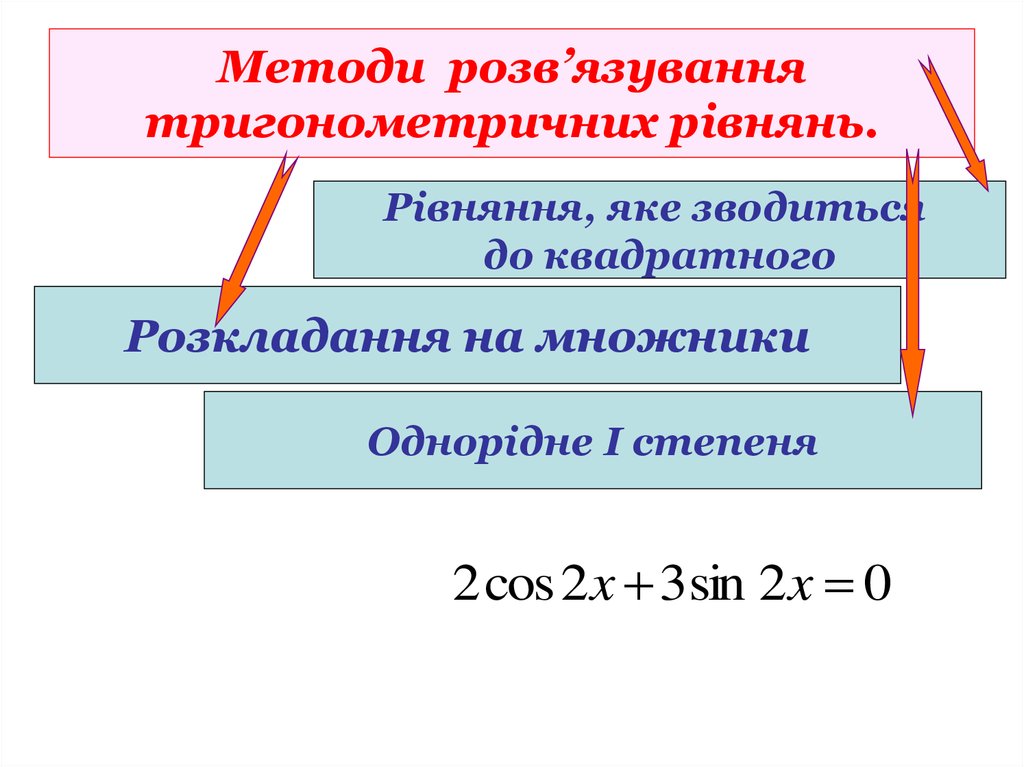
14. Методи розв’язування тригонометричних рівнянь.
Рівняння, яке зводитьсядо квадратного
Розкладання на множники
Однорідне І степеня
Однорідне ІІ степеня
3 sin x 4 sin x cos x cos x 0
2
2
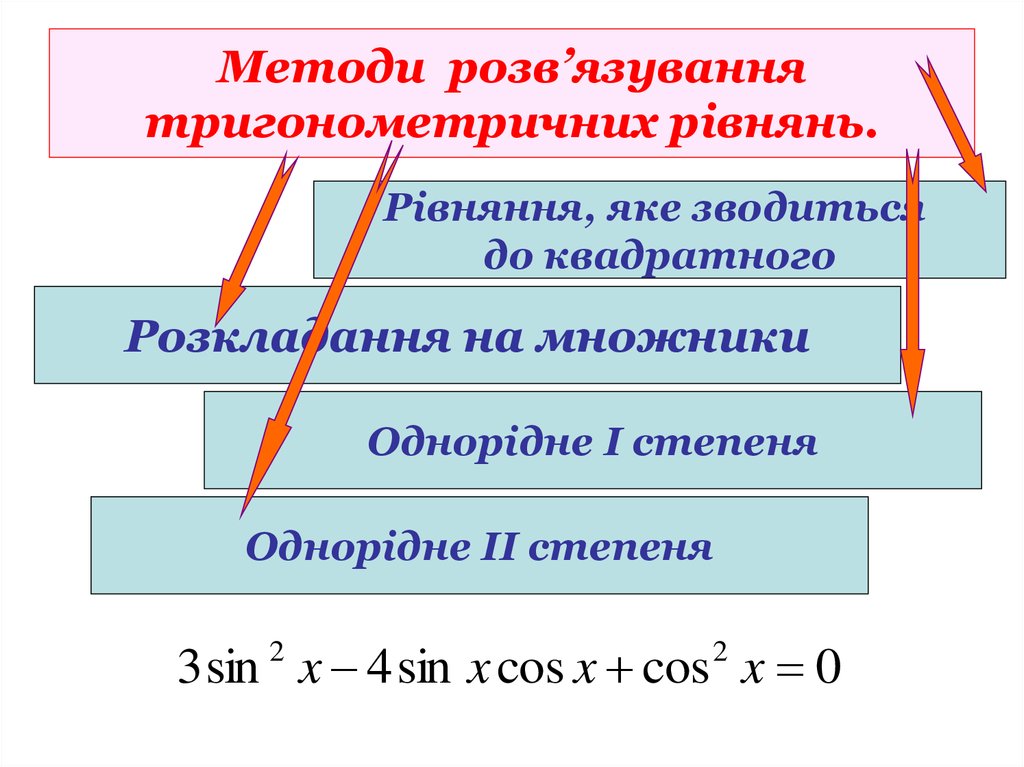
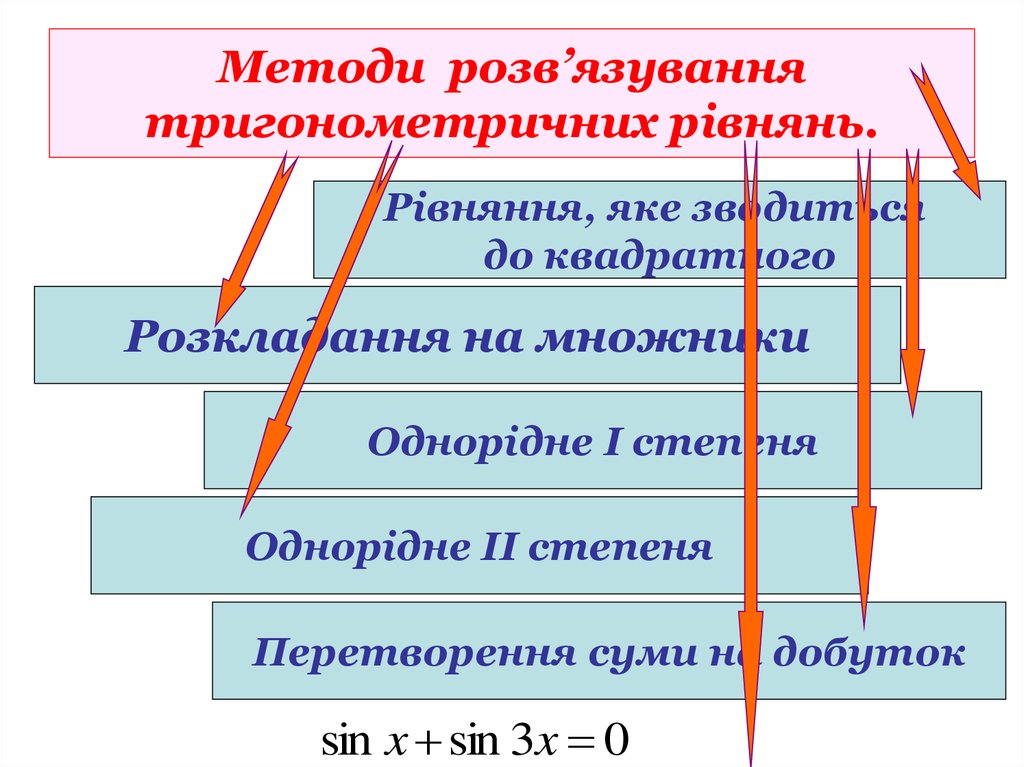
15. Методи розв’язування тригонометричних рівнянь.
Рівняння, яке зводитьсядо квадратного
Розкладання на множники
Однорідне І степеня
Однорідне ІІ степеня
Перетворення суми на добуток
sin x sin 3x 0
16. Формули квадратів половинних кутів:
Застосування формул пониження степеняФормули квадратів половинних кутів:
1 cos
1 cos
2
2
cos
sin
2
2
2
2
Формули пониження степеня:
1
sin 1 cos 2
2
2
1
cos 1 cos 2
2
2
17.
Застосування формул пониження степеня2sin2 x + cos 4x = 0
Розв’яжіть
рівняння
sin x sin 2 x sin 3x 1,5
2
2
2
18. Домашнє завдання:
Розв’яжітьрівняння
cos 2 x cos 2 2 x cos 2 3x 1,5










 Математика
Математика








