Похожие презентации:
Тригонометричні рівняння
1. Тригонометричні рівняння
Алгебра 102.
COS X = a, де|a| 1x = arccos a + 2 n,
n Z
3.
sin X = a, де|a| 1x=(–1)n arcsin a + n,
n Z
4.
tg x = a, де a Rx = arctg a + n,
n Z
5. Однорідні тригонометричні рівняння
Однорідним тригонометричним рівняннямназиваються рівняння у яких ліва частина є
многочленом , у кожному члені якого сума показників
степенів синуса і косинуса одного й того самого
аргумента однакова, а права частина - нуль.
Визначіть однорідність рівнянь:
5sinx=4cosx;
5sinx+4cosx=7;
3sin²x+4cos²x+5sinxcosx=0
5cosxsinx+sin²x-cos²x-4=0
6. Однорідні рівняння розв‘язуються методом ділення на синус, або косинус у найвищій степені, яка зустрічається в рівнянні.
7sinx-8cosx=07. Повторимо формули:
2tgx/2sinx=
1+tg²x/2
1-tg²x/2
cosx=
1+tg²x/2
8. Розв’яжіть рівняння:
3sinx+4cosx=59.
Sin2x=cos4x/2-sin4 x/210. Використання тригонометричної одиниці при роз’язуванні тригонометричних рівнянь
Тригонометричною одиницею щеназивають основну тригонометричну
тотожність sin²x+cos² x=1
5 sin²x+√3sinxcosx+6cos²x=5

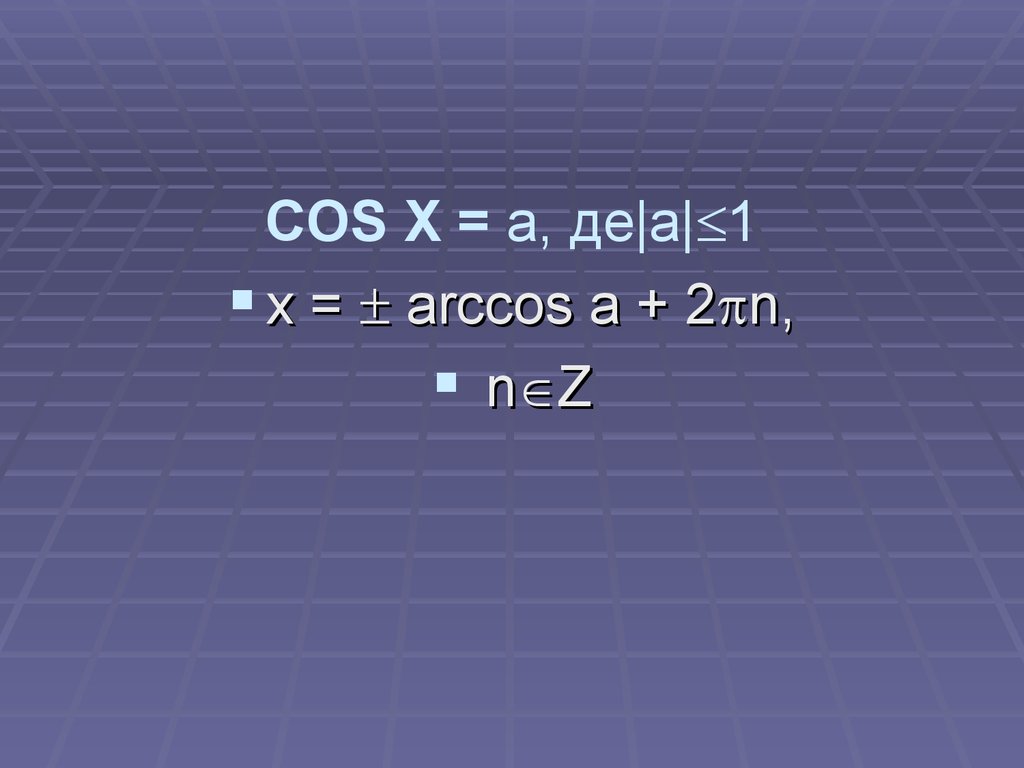

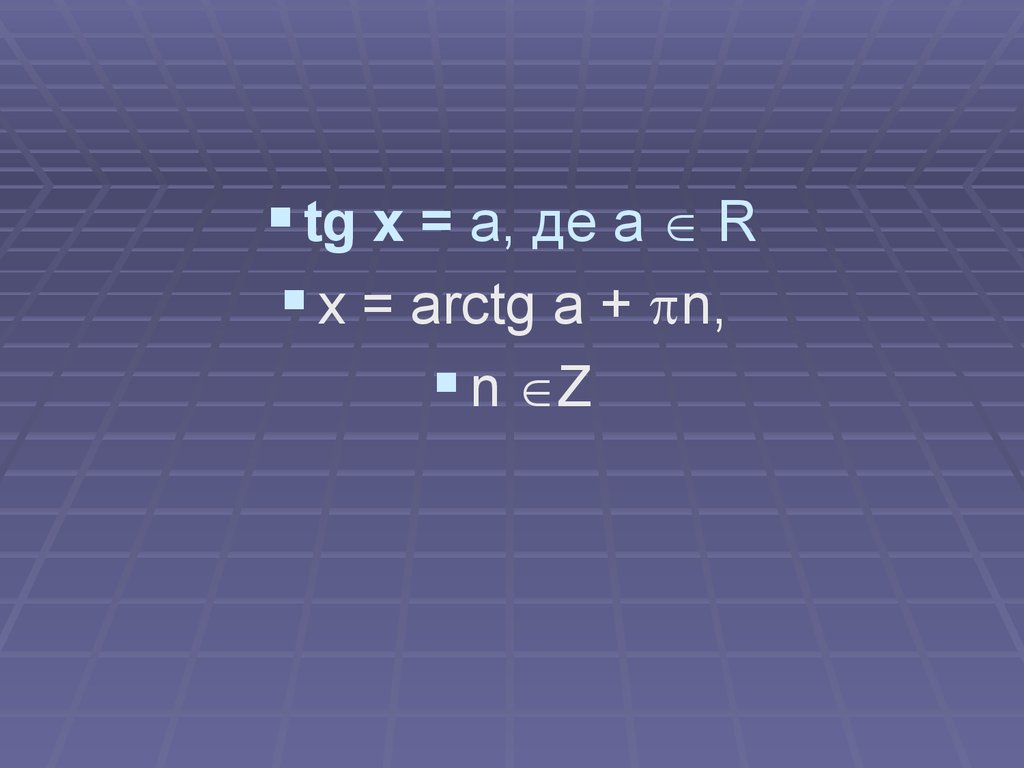






 Математика
Математика








