Автокореляція

1.

Автокореляція

2.

Зміст
1. Природа автокореляції. Основні поняття
та означення.
2. Тестування автокореляції. Критерій
Дарбіна-Уотсона.
3. Приклад тестування автокореляції.

3.

1. Природа автокореляції та її наслідки
Розглянемо класичну лінійну багатофакторну
модель
y a0 a1 x1 a2 x2 ... am xm u
або в матричному вигляді
Y = Ха + и
де y – вектор-стовпець залежної змінної розмірності n 1;
X – матриця незалежних змінних розміром n (m+1);
а – вектор-стовпець невідомих параметрів розмірності
(m+1) 1
u – вектор-стовпець випадкових помилок розмірності n 1
cov( u i , u j ) 0, i j

4.

Відсутність залежності між залишками
ui
ui k
і
буде гарантувати відсутність зв'язку і між
випадковими величинами
ui
і
ui 1
тобто між сусідніми відхиленнями.
Таким чином, коваріація
cov(ui , ui 1 ) 0, i 2,3,..., n

5.

У випадку, коли
cov(ui , ui 1 ) 0, i 2,3,..., n
залежність, а значить і кореляція між сусідніми
відхиленнями, буде існувати.
Ця кореляція називається автокореляцією
(послідовною кореляцією), і є показником наявності
зв'язку між упорядкованими в часі випадковими
величинами.

6.

Головними причинами автокореляції можуть бути: помилка
специфікації, інерційність в зміні економічних показників,
ефект павутиння.
1.Помилки специфікації.
В цьому випадку в моделі можуть бути не враховані
важливі пояснювальні змінні, або може бути неправильно
вибрана залежність між регресандом Y та регресорами Хi
що, як правило, викликає відхилення реальних значень
Y = уі від функції регресії.

7.

2. Інерційність.
Багатьом економічним показникам, наприклад,
інфляції, безробіттю, валовому продукту ВВП і т. ін.,
притаманна певна циклічність, яка пов'язана із
хвилеподібним явищем ділової активності.
Зайнятість
ВВП
Економічне
зростання
Безробіття
Інфляція

8.

3. Статистична обробка інформації.
При обробці статистичної інформації за певний період
часу використовують усереднені дані, одержані на
інтервалах часу, а це призводить до згладжування
коливань, які можуть існувати для кожного інтервалу,
що може бути однією з причин появи автокореляції.

9.

НАСЛІДКИ АВТОКОРЕЛЯЦІЇ
1. Оцінки параметрів моделі можуть бути
незміщеними, але неефективними, тобто
вибіркові дисперсії вектора оцінок а можуть бути
невиправдано великими.
2. Статистичні критерії t і F-статистик, які
отримані для класичної лінійної моделі, не
можуть бути використані для дисперсійного
аналізу, бо їх розрахунок не враховує наявності
коваріації залишків.
3. Неефективність оцінок параметрів
економетричної моделі, як правило, призводить
до неефективних прогнозів, тобто прогнозні
значення матимуть велику вибіркову дисперсію.

10.

Висновки. За наявності автокореляції
поширеним методом оцінювання
невідомих параметрів є узагальнений
метод найменших квадратів. Отримані за
допомогою УМНК оцінки є незміщеними
та ефективними.

11.

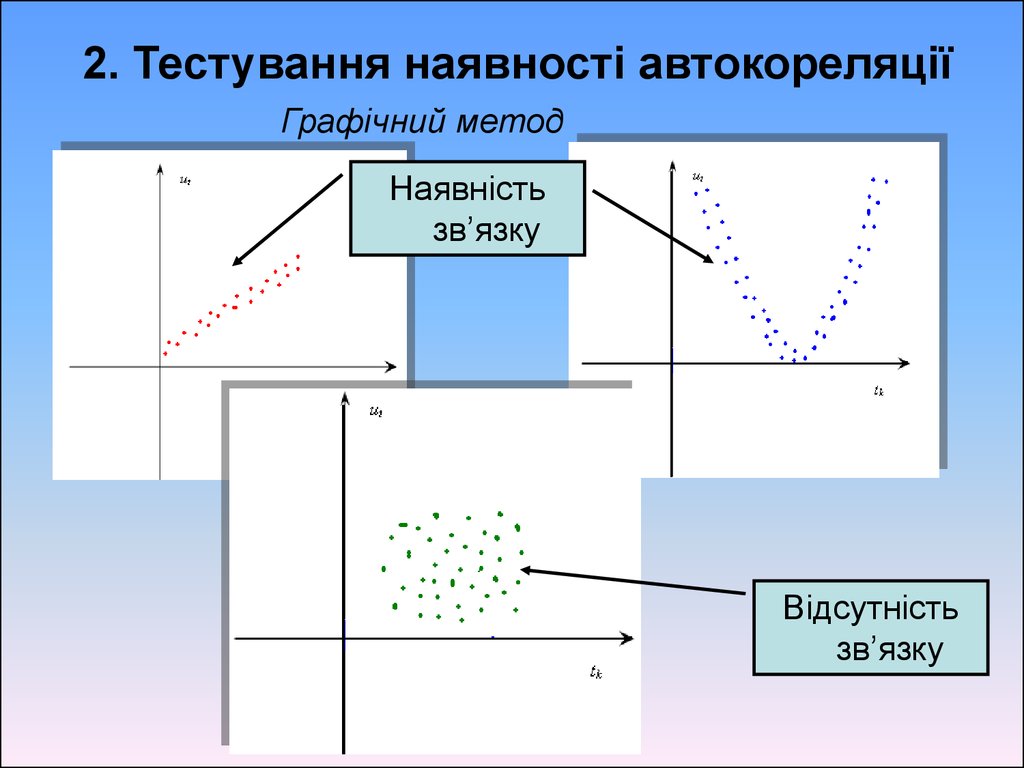
2. Тестування наявності автокореляції
Графічний метод
Наявність
зв’язку
Відсутність
зв’язку

12.

Тестування наявності автокореляції, як
правило, здійснюється за d-тестом
Дарбіна — Уотсона.
Інші тести: критерій фон Неймана,
нециклічний коефіцієнт автокореляції,
циклічний коефіцієнт автокореляції.

13.

Критерій Дарбіна — Уотсона
Крок 1. Розраховується значення d - статистики за
формулою
n
DW d
(u
t 2
t
ut 1 )
2
n
u
t 1
2
t
Зауваження. Доведено, що значення d -статистики
Дарбіна — Уотсона перебуває в межах
0 DW 4

14.

Крок 2. Задаємо рівень значущості α. За таблицею
Дарбіна — Уотсона при заданому рівні значущості α,
кількості факторів m і кількості спостережень n
знаходимо два значення
DW1 і DW2
0 DW DWто1 наявна додатна автокореляція.
Якщо
Якщо
DW1 DW DW2 або 4 DW2 DW 4 DW1
ми не можемо зробити висновки ані про наявність,
ані про відсутність автокореляції
DW
(потрапляє в зону невизначеності).

15.

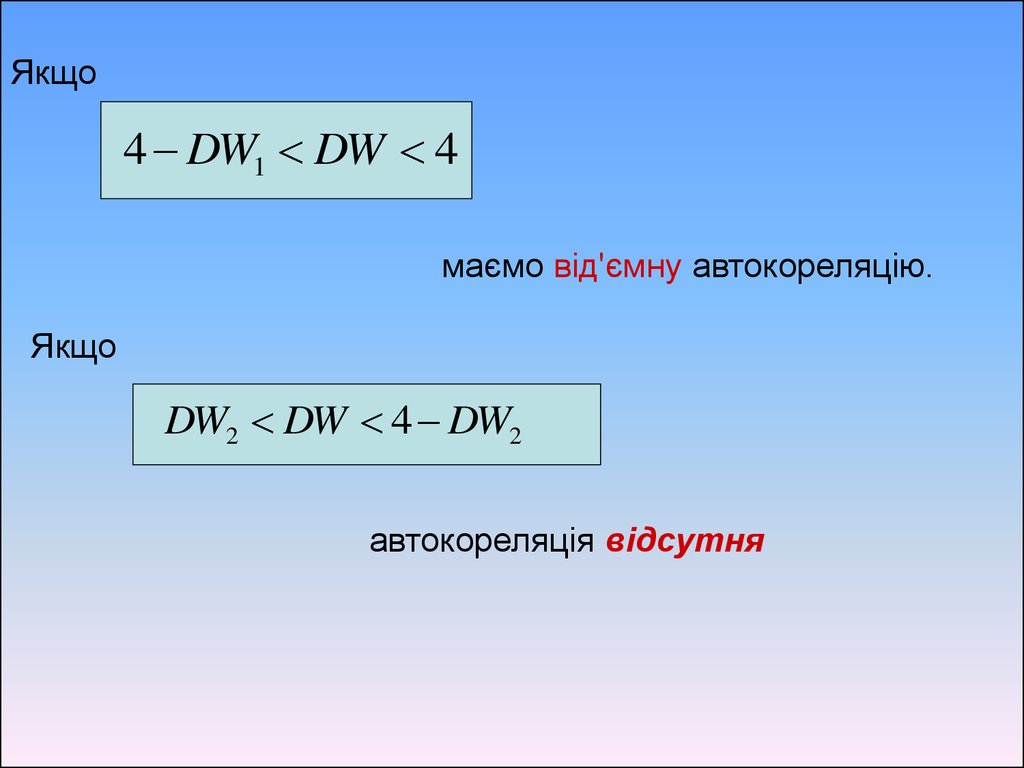
Якщо
4 DW1 DW 4
маємо від'ємну автокореляцію.
Якщо
DW2 DW 4 DW2
автокореляція відсутня

16.

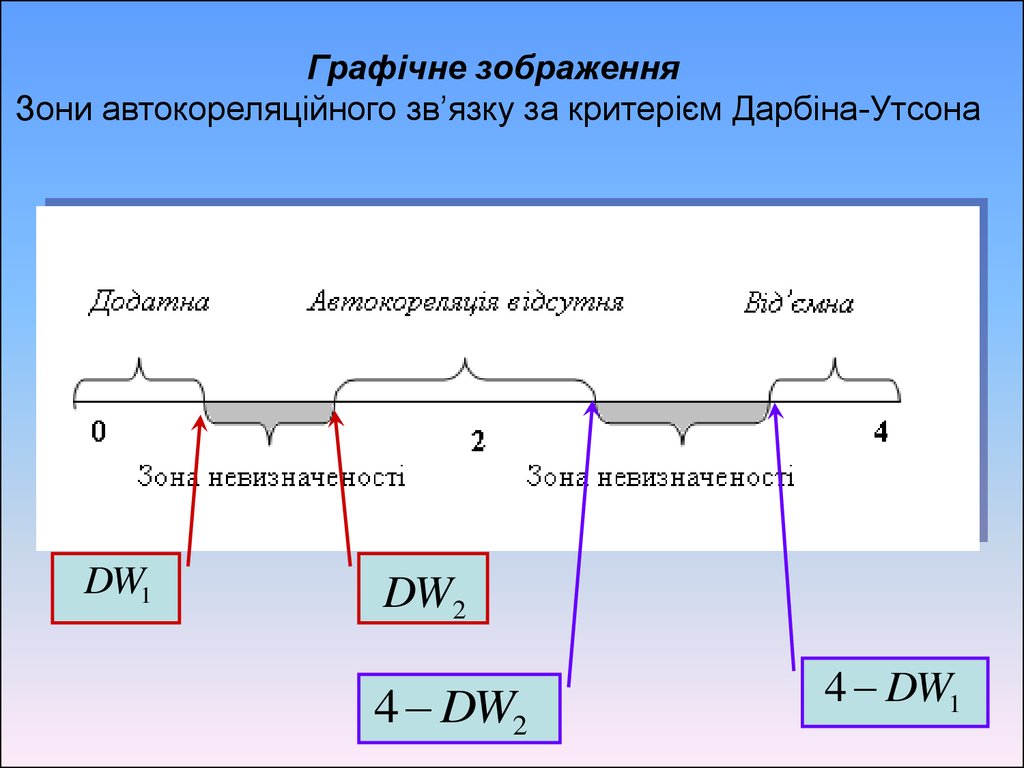
Графічне зображення
Зони автокореляційного зв’язку за критерієм Дарбіна-Утсона
DW1
DW2
4 DW2
4 DW1

17.

Критерій фон Неймана
Розраховується
n
Q Qфакт
2
(
u
u
)
t t 1
t 2
n
u
t 1
Звідси
Отже, при
2
t
n
n 1
n
Q DW
n 1
n Q DW

18.

Фактичне значення критерію фон Неймана
порівнюється з табличним при вибраному рівні
значущості α і заданій кількості спостережень:
Qтабл Q( ,n )
Якщо
Qфакт Qтабл
то існує додатна автокореляція.

19.

Приклад оцінювання параметрів моделі з
автокорельованими залишками
На основі двох взаємопов'язаних часових
рядів про роздрібний товарообіг і доходи
населення
побудувати
модель,
що
характеризує
залежність
роздрібного
товарообігу від доходу.
Спеціфікація моделі:
y– роздрібний товарообіг,
x– дохід.

20.

Залежність товарообігу від доходу
y = 2,3136+0,8683*x
33
32
31
y
30
29
28
27
26
25
27
28
29
30
31
x
32
33
34
35

21.

товарообіг
дохід
10
DW d
2
(
u
u
)
t t 1
t 2
10
2
u
t
t 1
2,3099
1,4782
1,5626
y = 2,3136+0,8683*x

22.

Задаємо α=0,05 і при n=10 і m=1 знайдемо за
таблицею d-статистику Дарбіна — Уотсона критичні
значення критерію:
DW1=0,879–нижня межа,
DW2 =1,320–верхня межа.
Оскільки
DW2 DW 4 DW2
то автокореляція відсутня.

23.

Параметризація моделі з автокорельованими
залишками
Параметри моделі з автокорельованими
залишками можна оцінити на основі чотирьох
методів:
1. Ейткена (УМНК);
2. Перетворення вихідної інформації;
3. Кочрена — Оркатта;
4. Дарбіна.

24.

Узагальнений метод найменших квадратів
(метод Ейткена)
Оператор оцінювання УМНК можна записати так:
1
1
1
aˆ ( X X ) X Y
T
T
де Ω-1-матриця, обернена до дисперсійноковаріаційної матриці залишків Ω.

25.

0
1
2
1
1
1
2
0
1
2
1
...
...
...
0
0
0
0
0
0 0
... ... ...
0 0 1
0
0
0
0

26.

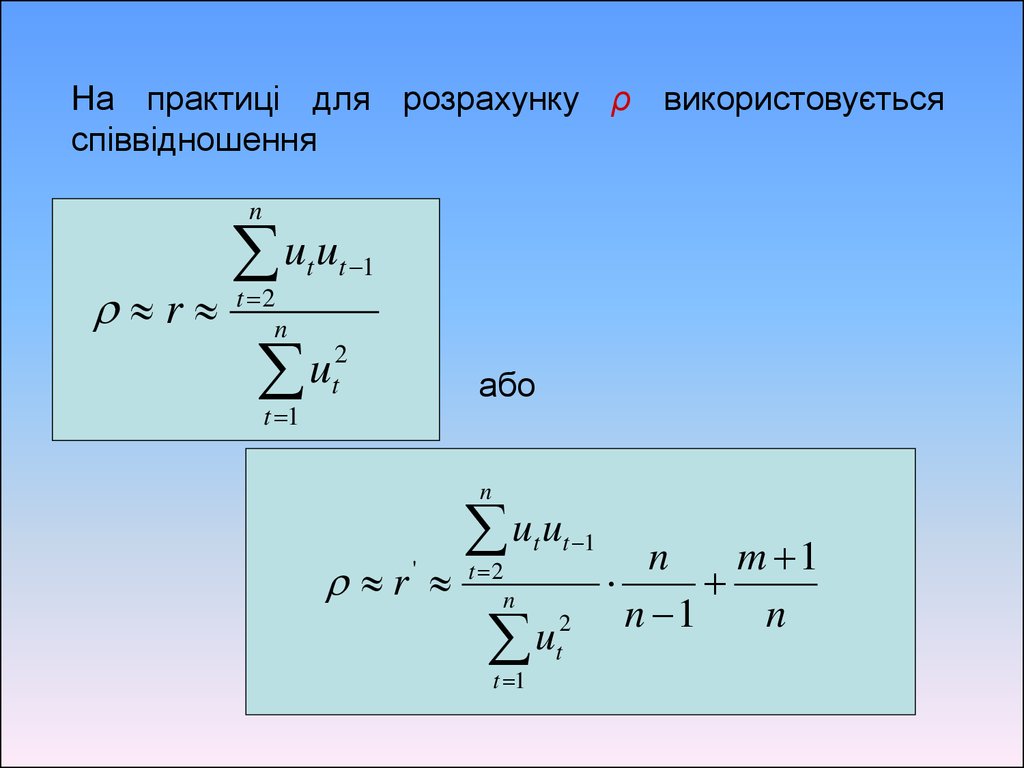
На практиці для розрахунку ρ використовується
співвідношення
n
r
u u
t 2
n
t t 1
u
t 1
2
t
або
n
r
'
u u
t 2
n
t t 1
u
t 1
2
t
n
m 1
n 1
n