Мультиколінеарність. (Тема 8)

1.

Назва
Назвадисципліни:
дисципліни:
ЕКОНОМЕТРИКА
ЕКОНОМЕТРИКА
Тема
Тема5:5:
МУЛЬТИКОЛІНЕАРНІСТЬ
МУЛЬТИКОЛІНЕАРНІСТЬ
Лектор:
Лектор:к.е.н.,
к.е.н.,доцент
доценткафедри
кафедриеконометрії
економетрії
та
тастатистики
статистикиДЕМЧИШИН
ДЕМЧИШИНМ.Я.
М.Я.

2. Навчальна мета:

Після вивчення теми студент повинен знати :
• поняття мультиколінеарності;
• методи оцінки ступеня мультиколінеарності;
• вплив мультиколінеарності на характеристики
економетричної моделі;
• методи усунення мультиколінеарності;
• алгоритм Фаррара-Глобера.

3.

План лекції
1.
Поняття, ознаки і наслідки існування
мультиколінеарності
2.
Виявлення мультиколінеарності в економетричній
моделі. Алгоритм Фаррара-Глобера
3.
Способи усунення мультиколінеарності. Метод
головних компонент

4.

Основна література
Єлейко В. Основи економетрії. – Львів: Марка Лтд, 1995. -191 с.
Єлейко В.І., Копич І.М., Боднар Р.Д., Демчишин М.Я. Економетрія: Навч.посібн.
– Львів: вид-во Львівської комерційної академії, 2007. – 420 с.
Корольов О.А. Економетрія: Лекції, питання, тести, задачі, ситуації, проблеми:
Навч. посібник. -К.: КДТЕУ, 2000. - 724 с.
Лещинський О.Л. Економетрія: Навч. посібн. для студ. вищ. навч. закл. / О.Л.
Лещинський, В.В. Рязанцева, О.О. Юнькова. – К.: МАУП, 2003. – 208 с.
Лук'яненко І.Г., Краснікова Л.І. Економетрика: Підручник. - К.: Т-во "Знання",
КОО, 1998.-494 с.
Наконечний С.I., Терещенко Т.О. Економетрiя: Навч. посiб. для сам ост. вивч.
диск. - К.: КНЕУ, 2001.- 192 с.
Толбатов Ю.А. Економетрика: Підручник. – К.: Четверта хвиля, 1997. – 320 с.

5. Питання 1. Поняття, ознаки і наслідки існування мультиколінеарності

Мультиколінеарність означає існування тісної
лінійної залежності, або кореляції, між двома чи
більше пояснювальними змінними.

6. Ознаки мультиколінеарності

1.
Якщо серед парних коефіцієнтів кореляції пояснювальних змінних є такі,
рівень яких наближається до множинного коефіцієнта кореляції або дорівнює
йому, це свідчить про можливість існування мультиколінеарності.
Інформацію про парну залежність може дати симетрична матриця
коефіцієнтів парної кореляції, або, як її ще називають, матриця кореляції
нульового порядку (р - кількість пояснювальних змінних):
rx1x1
rx2 x1
r
r
x3 x1
...
rx x
p1
rx1x2
rx2 x2
rx3 x2
...
rx p x2
rx1x3
rx2 x3
rx3 x3
...
rxpx3
...
...
...
...
...
rx1x p
rx2 x p
rx3 x p
...
rx p x p
!!! Явище мультиколінеарності в жодному разі не зводиться
лише до існування парної кореляції між пояснюючими
змінними.

7.

2. Загальніша перевірка передбачає застосування визначника (детермінанта)
матриці r, який називається детермінантом кореляції і r
позначається
Числові значення детермінанта кореляції містяться на інтервалі
r 0
-
існує повна мультиколінеарність.
r 1
-
мультиколінеарність відсутня.
r 0;1
Чим ближче r
до нуля, тим певніше можна стверджувати, що між пояснюючими
змінними існує мультиколінеарність.
Незважаючи на те, що числове значення r зазнає впливу дисперсії пояснюючих змінних, цей
показник можна вважати точковою мірою рівня мультиколінеарності.

8.

2
3. Коли коефіцієнт детермінації R , який обчислено для регресійних
залежностей між однією пояснюючою змінною та іншими такими
змінними, близький до одиниці, то можна говорити про наявність
мультиколінеарності.
F
F
x
k факт
табл
k
4. Якщо
, то
мультиколінеарна з іншими, тобто
залежить від інших незалежних змінних і треба вирішити питання про
вилучення з переліку змінних однієї з них.
5. Якщо
собою.
t kj факт t табл
, то
xk
і
xj
тісно пов’язані між
Аналізуючи F- і t-критерії, можна зробити висновок, яку із змінних
треба вилучити з розгляду в побудованій моделі для усунення
мультиколінеарності (треба при цьому виходити і з економіко-логікотеоретичних міркувань).

9. Основні наслідки мультиколінеарності в економетричній моделі:

• Зміщення оцінок параметрів моделі, обчислених
методом найменших квадратів.
• Збільшення дисперсії та коваріації оцінок параметрів
моделі, обчислених методом найменших квадратів, і,
відповідно, збільшення довірчих інтервалів для
параметрів і зниження точності їх оцінювання.
• Незначущість параметрів моделі, обчислених
методом найменших квадратів.
• Чутливість оцінок параметрів моделі до сукупності
спостережень, зокрема до обсягу вибірки.

10.

Питання 2.
Виявлення мультиколінеарності в
економетричній моделі.
Алгоритм Фаррара-Глобера

11. ПОКРОКОВИЙ АЛГОРИТМ ФАРРАРА-ГЛОБЕРА

Алгоритм містить три види статистичних критеріїв, згідно з якими
перевіряється відповідно мультиколінеарність:
•а) усього масиву пояснюючих змінних (χ2-критерій “хі-квадрат”);
•б) кожної пояснюючої змінної з рештою пояснюючих змінних
(F-критерій);
•в) кожної пари пояснюючих змінних (t-критерій).
Усі ці критерії при порівнянні з їх критичними значеннями дають
змогу зробити конкретні висновки щодо наявності чи відсутності
мультиколінеарності пояснюючих змінних.

12. Крок 1. НОРМАЛІЗАЦІЯ ЗМІННИХ

Нехай x1 , x2 , x3 ,..., xm – вектори пояснювальних змінних
економетричної моделі.
Елементи стандартизованих векторів обчислимо за формулою:
xik
*
xik xk
xk
де n – число спостережень ( i 1, n );
m – число пояснювальних (незалежних) змінних ( k 1, m );
xk – середня арифметична k-ї пояснювальної змінної;
2
xk - дисперсія k-ї пояснювальної змінної.

13. Крок 2. Знаходження КОРЕЛЯЦІЙНОЇ МАТРИЦІ 1-го порядку

rx1x1
rx2 x1
r rx3 x1
...
r
xk x1
rx1x2
rx1x3
...
rx2 x2
rx2 x3
...
rx3 x2
rx3 x3
...
...
...
...
rxk x2
rxk x3
...
rx1xk
rx2 xk
rx3 xk
...
rxk xk
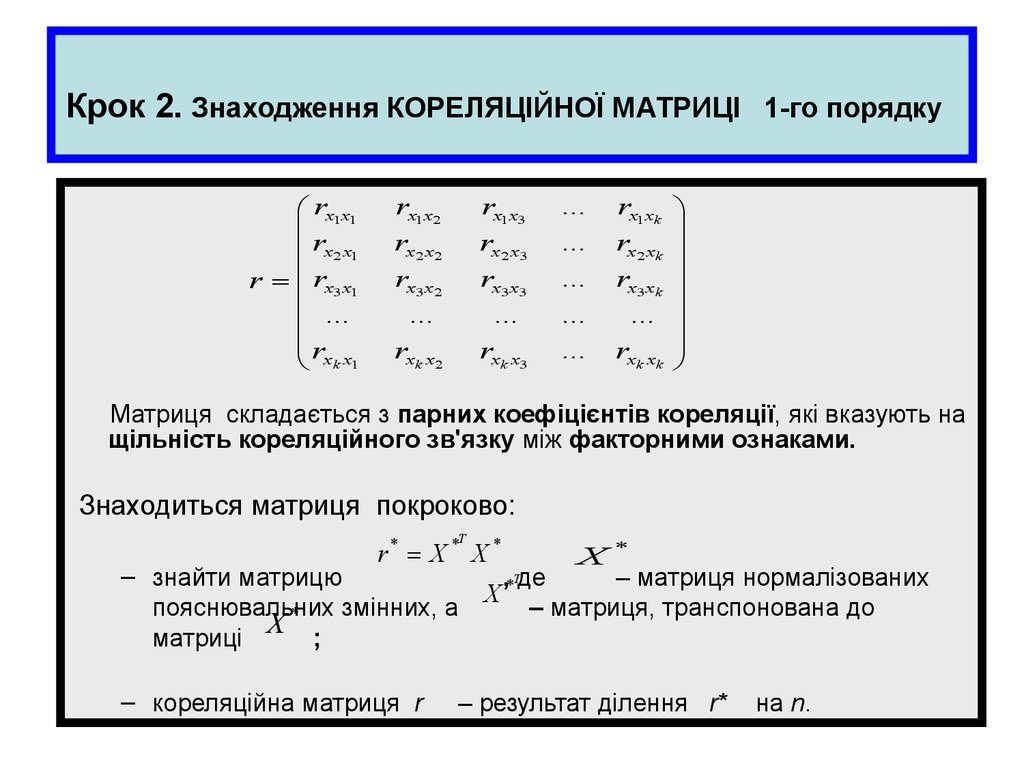
Матриця складається з парних коефіцієнтів кореляції, які вказують на
щільність кореляційного зв'язку між факторними ознаками.
Знаходиться матриця покроково:
T
r* X * X *
– знайти матрицю
пояснювальних
змінних, а
*
X
матриці
;
– кореляційна матриця r
X
*
, Tде
– матриця нормалізованих
X*
– матриця, транспонована до
– результат ділення r*
на n.

14. Крок 3.

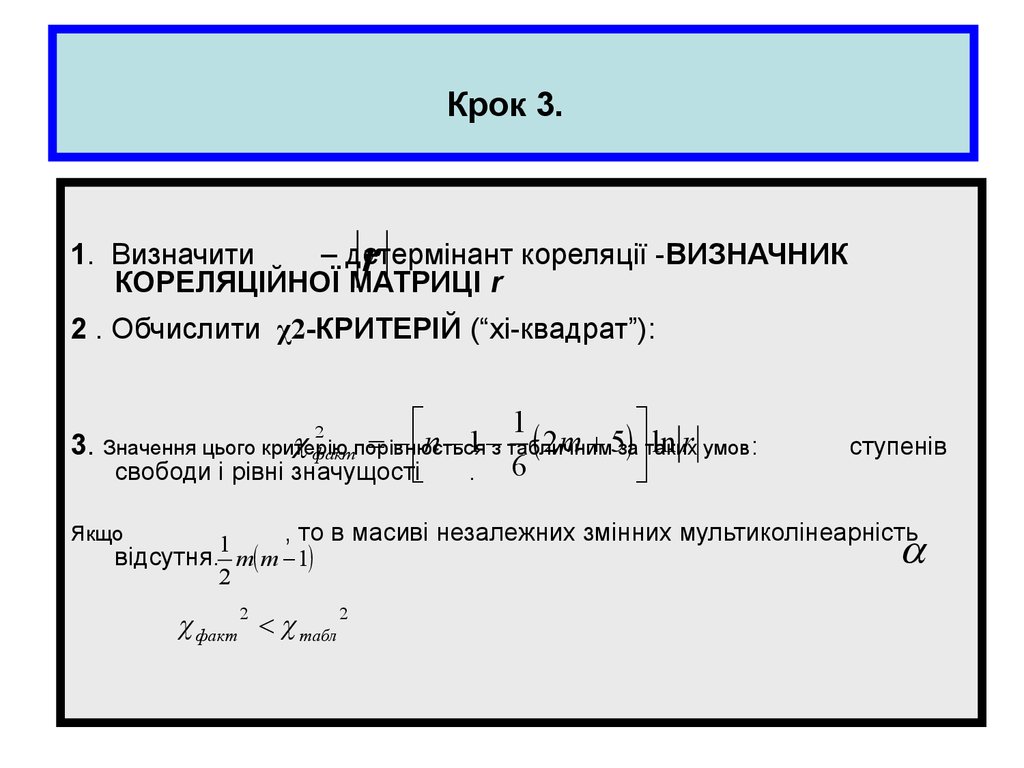
r
1. Визначити
– детермінант кореляції -ВИЗНАЧНИК
КОРЕЛЯЦІЙНОЇ МАТРИЦІ r
2 . Обчислити χ2-КРИТЕРІЙ (“хі-квадрат”):
свободи і рівні значущості
1
6
2m 5за таких
фактпорівнюється
n 1 з табличним
ln r умов:
3. Значення цього критерію
2
.
ступенів
, то в масиві незалежних змінних мультиколінеарність
1
відсутня. m m 1
2
Якщо
факт 2 табл 2

15. Крок 4. ВИЗНАЧЕННЯ МАТРИЦІ ПОМИЛОК С

Матриця помилок С – це матриця,
обернена до кореляційної матриці r:
С r
c11 c12
C c21 c22
c
31 c32
1
c13
c23
c33

16. Крок 5.

1.
РОЗРАХУНОК F-КРИТЕРІЇВ:
де
2.
n m
Fk факт (c kk 1)
– діагональні елементи матриці С, тобто сm, с 1
,с
11
ckk
22
33
і т.д.
Фактичні значення критеріїв порівнюються з табличним при (m-1) і (n-m)
ступенях свободи і рівні значущості
.
Якщо
, відповідна k-та пояснююча змінна мультиколінеарна з
іншими.
3.
Fкоефіцієнти
k факт Fтабл
Обчислити
детермінації для кожної змінної
Rk2 1
1
ckk
:

17. Крок 6. Знаходження ЧАСТИННИХ КОЕФІЦІЄНТІВ КОРЕЛЯЦІЇ

rkj
де
ckj
ckk
ckj
ckk c jj
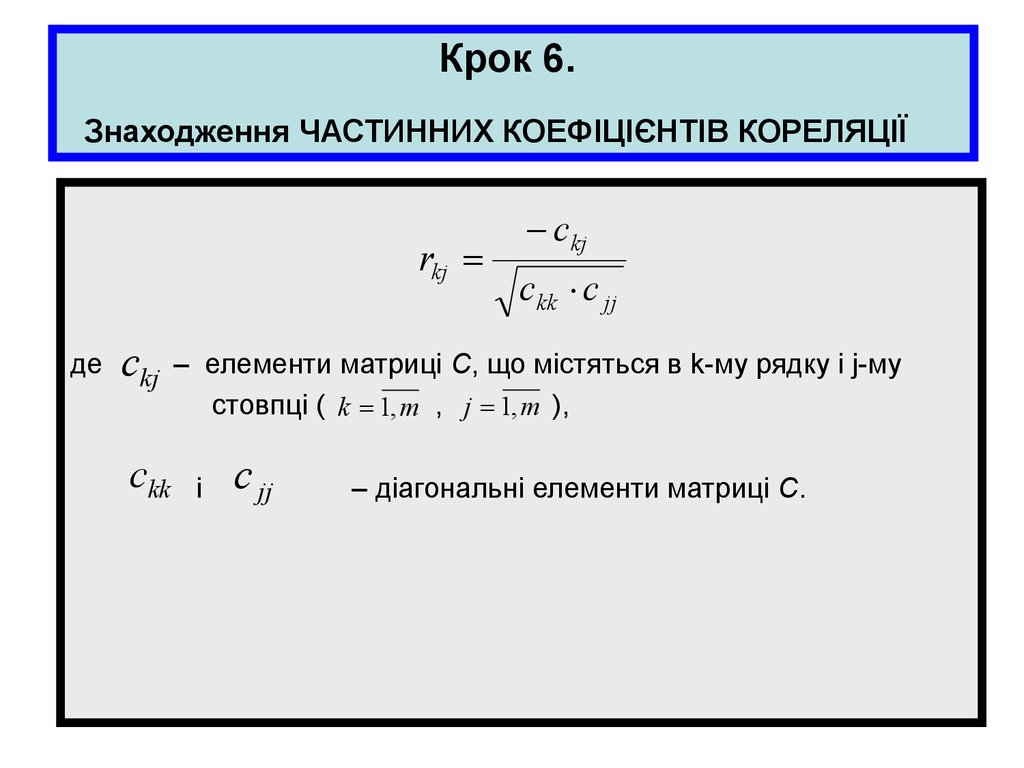
– елементи матриці С, що містяться в k-му рядку і j-му
стовпці ( k 1, m , j 1, m ),
і
c jj
– діагональні елементи матриці С.

18. Крок 7. РОЗРАХУНОК t-КРИТЕРІЇВ

t kj
rkj n m
1 rkj
2
Фактичні значення критеріїв порівнюються з табличним
за n-m ступенів свободи і рівня значущості
.
Якщо
t kj t табл
, між змінними
xk і x j існує мультиколінеарність.

19.

Питання 3.
Способи усунення мультиколінеарності.
Метод головних компонентів

20. Методи усунення мультиколінеарності

•Використання додаткової або первинної
інформації
• Об’єднання інформації.
•Відкидання змінної з високою кореляцією.
•Перетворення даних (використання перших
різниць).
•Збільшення кількості спостережень

21.

Метод головних компонентів застосовується для оцінювання
параметрів регресійних моделей з великою кількістю факторних
змінних у випадку, коли ці фактори мають однакові одиниці
вимірювання.
Суть методу головних компонентів полягає в заміні сукупності
факторних змінних на нові змінні, які між собою були б попарно
некорельованими і впорядкованими в порядку спадання їх
дисперсій.

22.

Алгоритм методу головних компонентів

23. Крок 1. Нормалізація факторних змінних

Нехай
x1 , x2 , x3 ,..., x p
економетричної моделі.
– вектори пояснювальних змінних
Елементи стандартизованих векторів обчислимо за формулою:
x
*
ji
x ji x j
xj
i=1, 2, …, n; j=1, 2, …, p,
де n – кількість спостережень;
p – кількість факторів у моделі,
– середнє арифметичне j-го фактора;
xj
xj
- середньоквадратичне відхилення j-ої факторної змінної. .

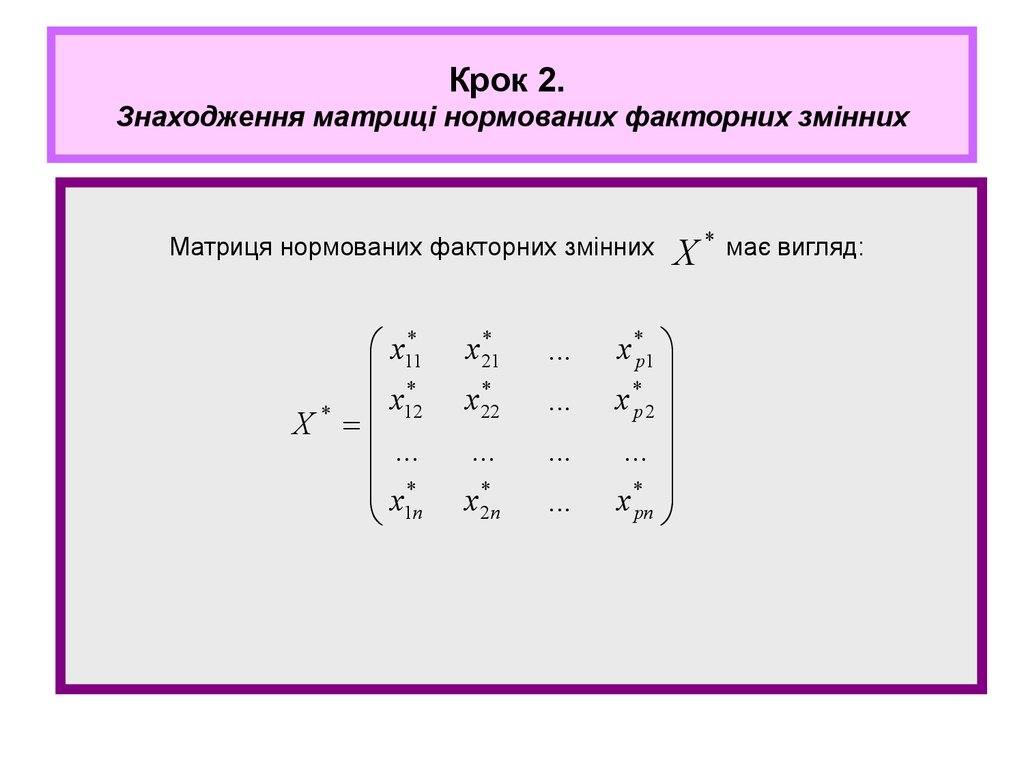
24. Крок 2. Знаходження матриці нормованих факторних змінних

Матриця нормованих факторних змінних
x11*
*
x12
*
X
...
x*
1n
*
x 21
...
*
x 22
...
...
...
x 2*n
...
X * має вигляд:
x *p1
*
x p2
...
x *pn

25. Крок 3. Знаходження кореляційної матриці

Кореляційна матриця або матриця моментів нормалізованої системи
нормальних рівнянь r знаходиться за формулою:
r
1 *T *
X X
n
де X *T– матриця, транспонована до матриці .
Кореляційна матриця матиме вигляд:
,
де
1
r12
r r13
...
r
1p
r21
1
r31
r32
...
...
r23
...
1
...
...
...
r2 p
r3 p
...
r p1
rp 2
rp3
...
1
rij rxi x j– парні коефіцієнти кореляції, i≠j, i=1, 2, …, n; j=1, 2, …, p.

26. Крок 4. Знаходження власних чисел кореляційної матриці

Власні числа 1,
2 , …, p
є розв’язками рівняння
r I 0
де І – одинична матриця розмірності
p p.

27. Крок 5. Ранжування власних чисел кореляційної матриці

Впорядкуємо власні числа
1 ,
2
,… ,
в порядку спадання їх абсолютних значень.
.
p

28. Крок 6. Знаходження власних векторів кореляційної матриці

З системи рівнянь
r I a 0
знаходимо власні вектори
a i , i = 1, 2, …, p,
при умові, що виконується співвідношення
1,
aiT a j
0,
де
a iT
якщо
i j;
якщо
i j,
– вектор, транспонований до
ai
.

29. Крок 7. Знаходження головних компонентів власних векторів кореляційної матриці

Головні компоненти знаходимо зі співвідношення
Z i X * ai
i = 1, 2, …, p
Вони повинні задовольняти наступні умови
n
z
j 1
ij
0
1 T
Z i Z i i
n
Z kT Z i 0
i = 1, 2, …, p;
i = 1, 2, …, p;
i≠k,
i, k = 1, 2, …, p.

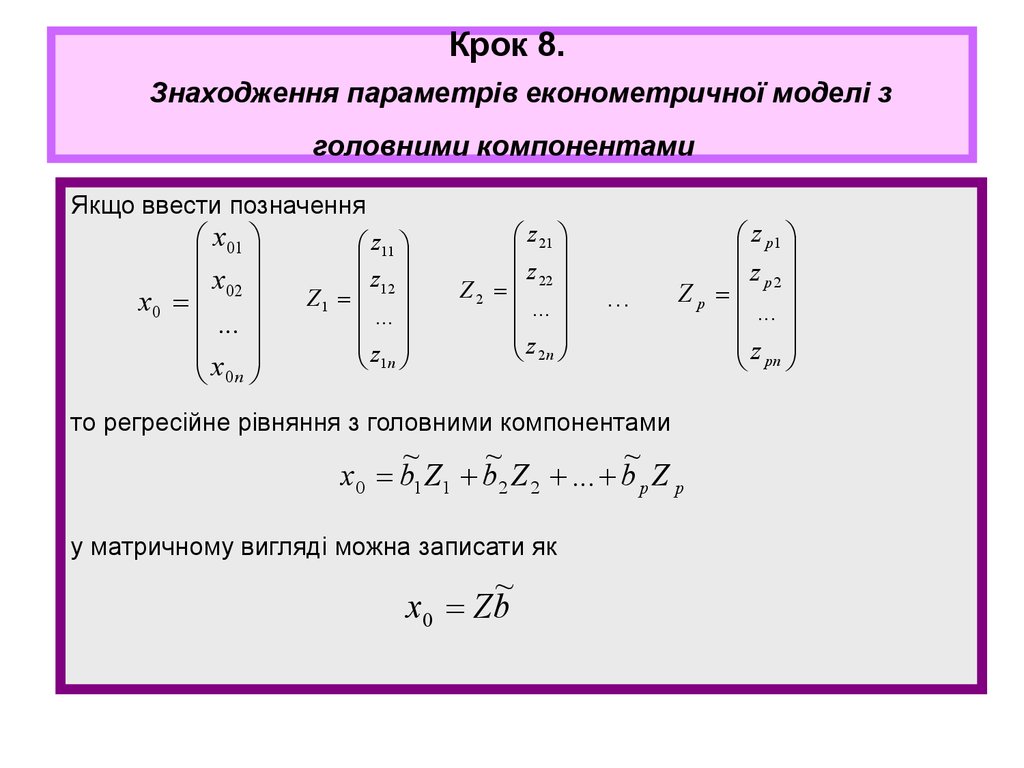
30. Крок 8. Знаходження параметрів економетричної моделі з головними компонентами

Якщо ввести позначення
x01
z11
x
z12
02
Z
x0
1
...
...
z
1n
x0 n
z 21
z
Z 2 22
...
z
2n
…
z p1
z p2
Zp
...
z
pn
то регресійне рівняння з головними компонентами
~
~
~
x0 b1 Z1 b2 Z 2 ... b p Z p
у матричному вигляді можна записати як
~
x 0 Zb

31. Крок 8. Знаходження параметрів економетричної моделі з головними компонентами

Невідомі параметри
~
~
b1 , b2
, …,
~
b p знаходяться із співвідношення
~
b Z 1 x0
де
Z 1
– матриця, обернена до матриці Z.

32. Крок 9. Визначення параметрів вихідної моделі

Для моделі
де
x11
x12
X
...
x
1n
x0 Xb
x 21
...
x 22
...
x2n
...
...
...
невідомі параметри
x p1
x p2
...
x pn
b1
b2
b
...
,
b
p
і
b1 , b2 , …, bp знаходяться із співвідношення
~
b Ab
де матриця А складається з власних векторів
a11
a12
A
...
a
1p
a 21
...
a 22
...
...
...
a2 p
...
a p1
a p2
...
a pp
ai
, i = 1, 2, …, p: