Похожие презентации:
ТПР. Многокритериальная оптимизация. (Занятие 6)
1.
ОСНОВЫ ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙЗанятие 6
2
Исправление опечатки:
В презентации 5 в разделе «Метод Гаусса-Зайделя» изменяемый характер фактора
следует обозначать термином «variable» или сокращённо «varia» (но не «varium»)
6. МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ
6.1 Постановка задачи:
Найти сочетание значений факторов,
Х1
К1 которое обеспечивает такое сочетание
значений критериев оптимизации,
ОБЪЕКТ
Х2
К2
которое наилучшим образом удовлет. . . . . . . ОПТИМИЗАЦИИ . . . . . . .
Хn
Кm воряет требованиям к качеству объекта
оптимизации.
*
*
*
{Х1 , Х2 , . . . Хn } = ?
В большинстве практических случаев назначенные критерии оптимизации
находятся в противоречии: улучшение одного критерия может сопровождаться
ухудшением других критериев. Поэтому точного и однозначного математического
решения такие оптимизационные задачи, как правило, не имеют.
Речь может идти только о более или менее формализованном поиске некоего
компромиссного варианта. Методов поиска таких компромиссов известно довольно
много. Но мы с Вами ограничимся рассмотрением только тех, которые приведены
в правой части классификации.
2.
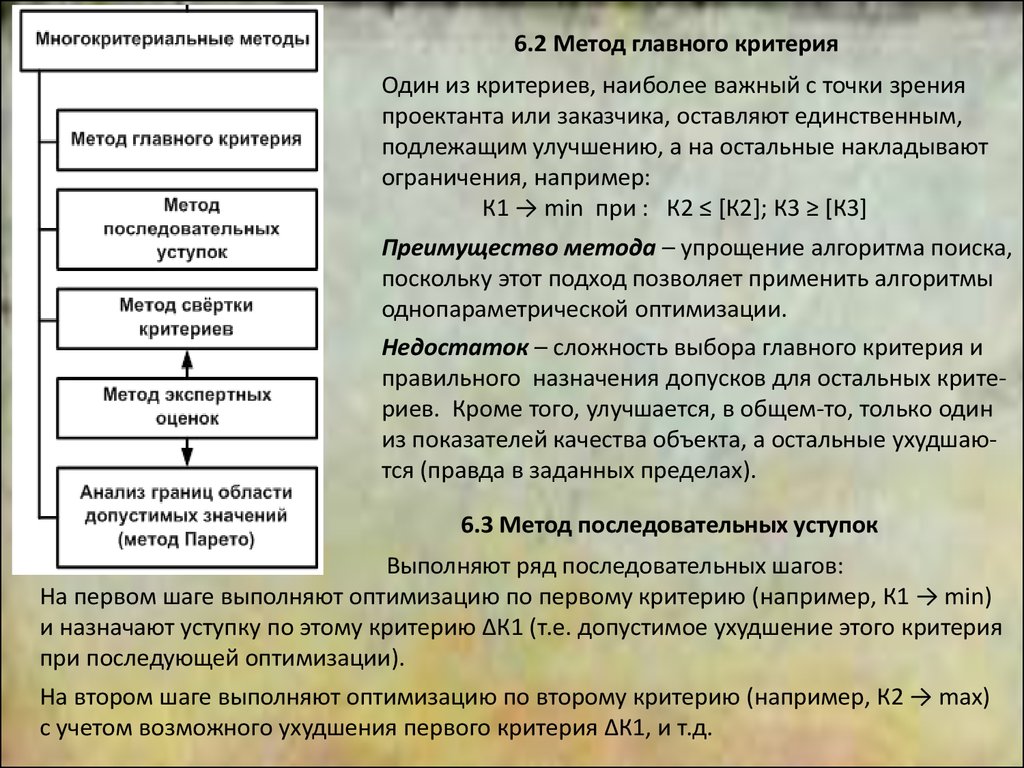
6.2 Метод главного критерия2
Один из критериев, наиболее важный с точки зрения
проектанта или заказчика, оставляют единственным,
подлежащим улучшению, а на остальные накладывают
ограничения, например:
К1 → min при : К2 ≤ [К2]; К3 ≥ [К3]
Преимущество метода – упрощение алгоритма поиска,
поскольку этот подход позволяет применить алгоритмы
однопараметрической оптимизации.
Недостаток – сложность выбора главного критерия и
правильного назначения допусков для остальных критериев. Кроме того, улучшается, в общем-то, только один
из показателей качества объекта, а остальные ухудшаются (правда в заданных пределах).
6.3 Метод последовательных уступок
Выполняют ряд последовательных шагов:
На первом шаге выполняют оптимизацию по первому критерию (например, К1 → min)
и назначают уступку по этому критерию ΔК1 (т.е. допустимое ухудшение этого критерия
при последующей оптимизации).
На втором шаге выполняют оптимизацию по второму критерию (например, К2 → mах)
с учетом возможного ухудшения первого критерия ΔК1, и т.д.
3.
2Достоинство метода, по сравнению с предыдущим –
некоторое улучшение всех рассматриваемых критериев.
Недостатки: зависимость конечного результата от
правильного назначения последовательности оптимизируемых критериев и сложность обоснованного назначения
величин уступок.
6.4 Метод свёртки критериев
В качестве оптимизируемого показателя используется комплексный критерий, отражающий систему предпочтения
конструктора (в теории принятия решений такой
комплексный критерий называют функцией ценности).
Чаще всего этому комплексному критерию придают форму
весовой функции:
K = b1K1 + b2K2 + … ,
где К1, К2 … – частные критерии, выраженные в относительной форме;
b1, b2 …– весовые коэффициенты, определяющие важность
соответствующих критериев.
По условию нормировки сумма весовых коэффициентов должна равняться 1.
Преимущество метода – комплексный учет всех частных критериев.
Недостаток – субъективный характер выбора значений весовых коэффициентов
4.
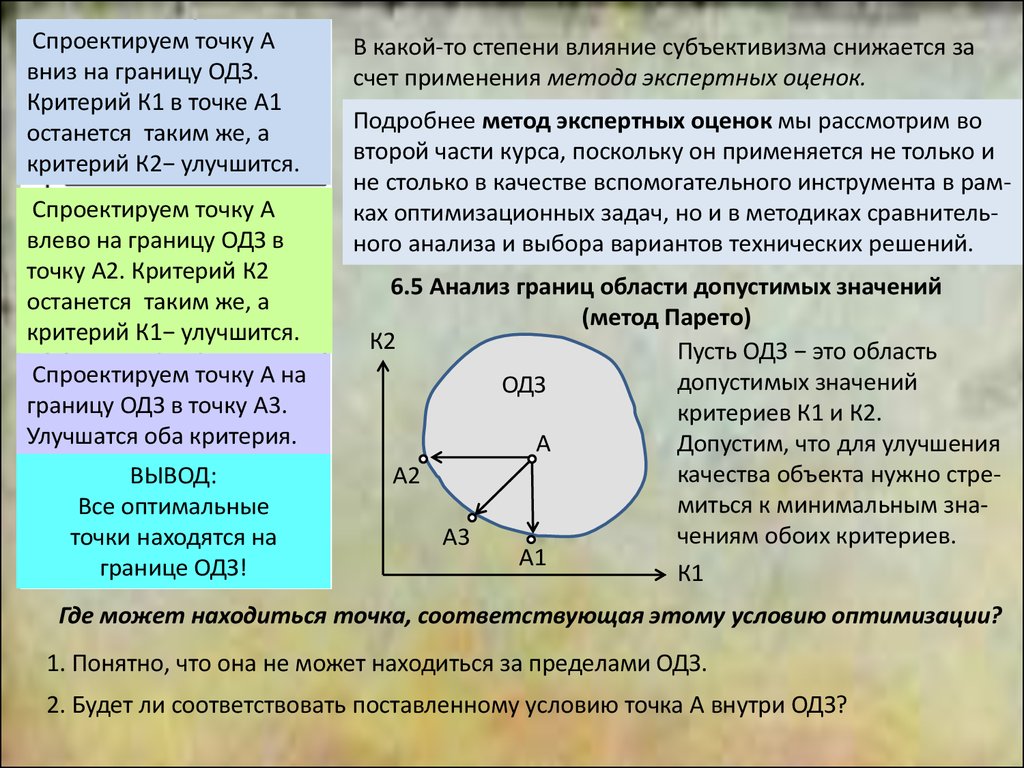
Спроектируем точку Авниз на границу ОДЗ.
Критерий К1 в точке А1
останется таким же, а
критерий К2− улучшится.
Спроектируем точку А
влево на границу ОДЗ в
точку А2. Критерий К2
останется таким же, а
критерий К1− улучшится.
Спроектируем точку А на
границу ОДЗ в точку А3.
Улучшатся оба критерия.
ВЫВОД:
Все оптимальные
точки находятся на
границе ОДЗ!
В какой-то степени влияние субъективизма снижается за
счет применения метода экспертных оценок.
2
Подробнее метод экспертных оценок мы рассмотрим во
второй части курса, поскольку он применяется не только и
не столько в качестве вспомогательного инструмента в рамках оптимизационных задач, но и в методиках сравнительного анализа и выбора вариантов технических решений.
6.5 Анализ границ области допустимых значений
(метод Парето)
К2
Пусть ОДЗ − это область
допустимых значений
ОДЗ
критериев К1 и К2.
Допустим, что для улучшения
А
качества объекта нужно стреА2
миться к минимальным значениям обоих критериев.
А3
А1
К1
Где может находиться точка, соответствующая этому условию оптимизации?
1. Понятно, что она не может находиться за пределами ОДЗ.
2. Будет ли соответствовать поставленному условию точка А внутри ОДЗ?
5.
2Итак, оптимальные решения следует искать на границе области допустимых значений
критериев оптимизации. Но граница, в принципе, является геометрическим местом
бесконечного множества решений. Нельзя ли как-то сузить район поиска?
Рассмотрим различные варианты постановки оптимизационных задач.
C
К2
1. Критерий К1 желательно сделать как кожно
больше, и он имеет приоритетное значение.
B
ОДЗ
А
D
Достаточно очевидно, что решение такой задачи отображается самой правой точкой границы ОДЗ. Для её нахождения достаточно провести вертикальную касательную к
правой части границы ОДЗ. (точка А)
2. Критерий К1 желательно сделать как кожно
меньше, и он имеет приоритетное значение.
К1
Решение такой задачи отображается самой левой точкой границы ОДЗ. Для её
нахождения достаточно провести вертикальную касательную к левой части границы
ОДЗ (точка B).
3. Критерий К2 желательно сделать как кожно больше, и он имеет
приоритетное значение.
Этому условию соответствует самая верхняя точка границы ОДЗ (точка C).
4. Критерий К2 желательно сделать как кожно меньше, и он имеет
приоритетное значение.
Этому условию соответствует самая нижняя точка границы ОДЗ (точка D).
6.
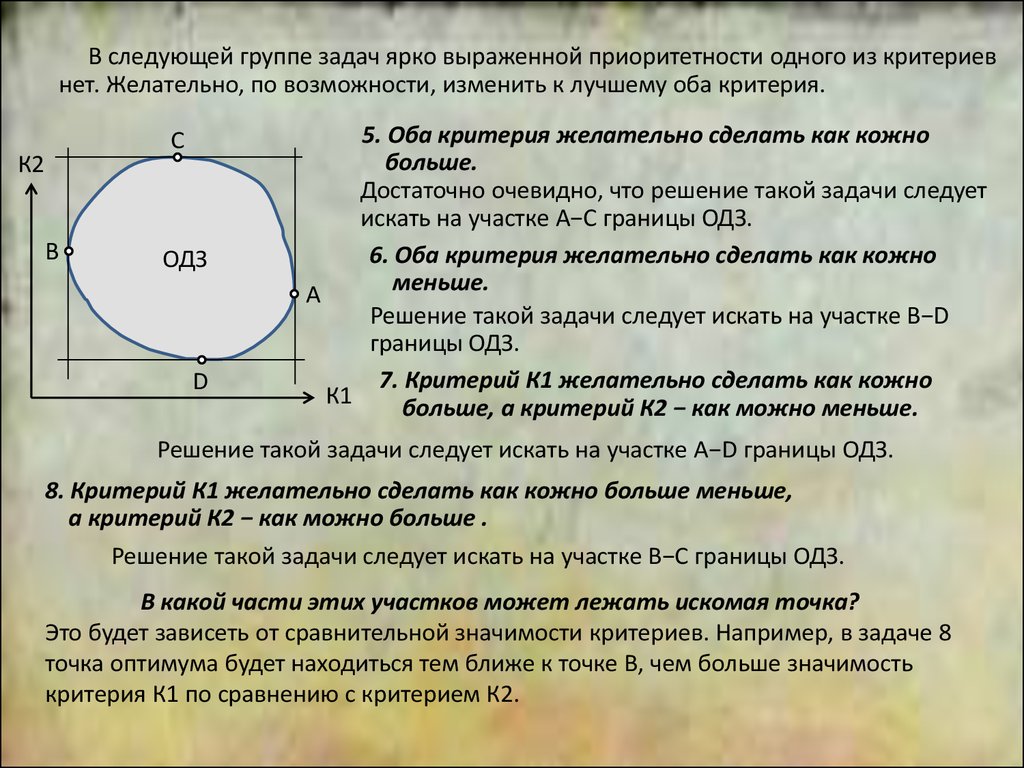
2В следующей группе задач ярко выраженной приоритетности одного из критериев
нет. Желательно, по возможности, изменить к лучшему оба критерия.
C
К2
B
ОДЗ
D
5. Оба критерия желательно сделать как кожно
больше.
Достаточно очевидно, что решение такой задачи следует
искать на участке A−C границы ОДЗ.
6. Оба критерия желательно сделать как кожно
меньше.
А
Решение такой задачи следует искать на участке B−D
границы ОДЗ.
7. Критерий К1 желательно сделать как кожно
К1
больше, а критерий К2 − как можно меньше.
Решение такой задачи следует искать на участке А−D границы ОДЗ.
8. Критерий К1 желательно сделать как кожно больше меньше,
а критерий К2 − как можно больше .
Решение такой задачи следует искать на участке B−C границы ОДЗ.
В какой части этих участков может лежать искомая точка?
Это будет зависеть от сравнительной значимости критериев. Например, в задаче 8
точка оптимума будет находиться тем ближе к точке B, чем больше значимость
критерия К1 по сравнению с критерием К2.
7.
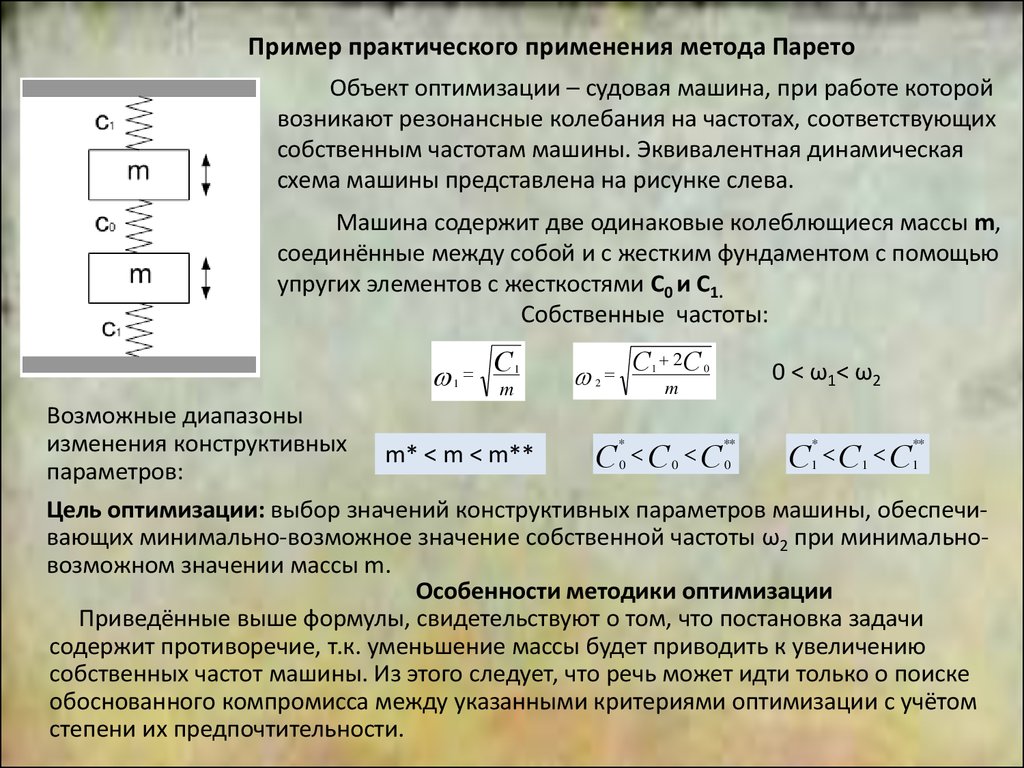
Пример практического применения метода Парето2
Объект оптимизации – судовая машина, при работе которой
возникают резонансные колебания на частотах, соответствующих
собственным частотам машины. Эквивалентная динамическая
схема машины представлена на рисунке слева.
Машина содержит две одинаковые колеблющиеся массы m,
соединённые между собой и с жестким фундаментом с помощью
упругих элементов с жесткостями С0 и С1.
Собственные частоты:
1
С
m
1
2
С 2С
1
m
0
0 < ω1< ω2
Возможные диапазоны
*
**
*
**
изменения конструктивных m* < m < m**
С1 С 1 С 1
С0 С0 С0
параметров:
Цель оптимизации: выбор значений конструктивных параметров машины, обеспечивающих минимально-возможное значение собственной частоты ω2 при минимальновозможном значении массы m.
Особенности методики оптимизации
Приведённые выше формулы, свидетельствуют о том, что постановка задачи
содержит противоречие, т.к. уменьшение массы будет приводить к увеличению
собственных частот машины. Из этого следует, что речь может идти только о поиске
обоснованного компромисса между указанными критериями оптимизации с учётом
степени их предпочтительности.
8.
2Будем решать задачу в 2 этапа.
На 1 этапе выполним анализ зоны возможных технических решений.
Пусть первым критерием будет квадрат второй собственной частоты: K 1 С1 С 0
m
Это позволит избавиться от возни с радикалом, а на результатах оптимизации не скажется, поскольку минимуму квадрата частоты будет соответствовать и
минимум самой частоты.
2
Вторым критерием пусть будет половина динамической массы машины:
(минимуму половины будет соответствовать и минимум всей массы).
Если перемножить критерии К1 и К2 получится уравнение
семейства гипербол в пространстве критериев:
Крайними в этом семействе будут гиперболы,
соответствующие крайним значениям
жёсткостей С1 и С0 :
К1 · К2 = С1 + 2С0
K К С 2С
*
1
2
К2 = m
1
*
0
K К С
1
2
**
1
2С 0
**
Эти кривые образуют две границы области допустимых состояний объекта.
Другие две границы образованы крайними значениями массы m
Переведём абсолютные значения критериев в относительные, выраженные в процентах.
Для этого достаточно разделить фактическое значение критерия на максимально
допустимое и умножить результат на 100%
9.
К2 ,%m**
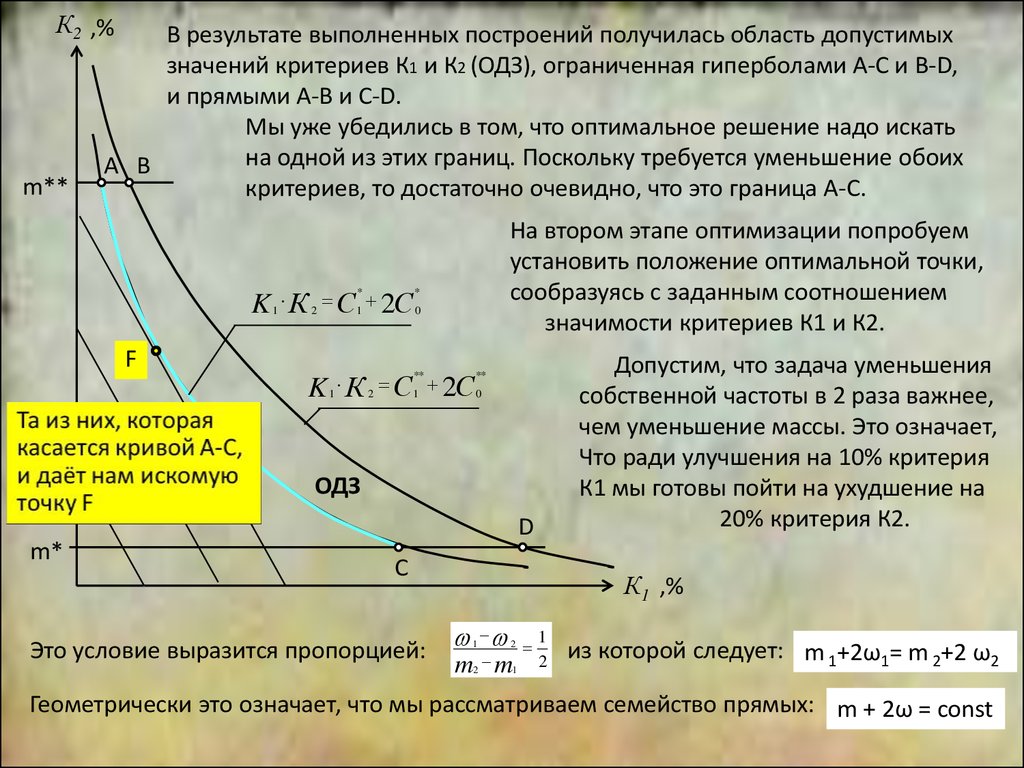
B результате выполненных построений получилась область допустимых 2
значений критериев К1 и К2 (ОДЗ), ограниченная гиперболами А-С и B-D,
и прямыми А-B и С-D.
Мы уже убедились в том, что оптимальное решение надо искать
на одной из этих границ. Поскольку требуется уменьшение обоих
А B
критериев, то достаточно очевидно, что это граница А-С.
K К С 2С
1
F
2
*
*
1
0
На втором этапе оптимизации попробуем
установить положение оптимальной точки,
сообразуясь с заданным соотношением
значимости критериев К1 и К2.
Допустим, что задача уменьшения
собственной частоты в 2 раза важнее,
чем уменьшение массы. Это означает,
Что ради улучшения на 10% критерия
К1 мы готовы пойти на ухудшение на
20% критерия К2.
K 1 К 2 С1 2С 0
**
**
ОДЗ
m*
D
C
Это условие выразится пропорцией:
К1 ,%
1
2
m m
2
1
1
2
из которой следует: m 1+2ω1= m 2+2 ω2
Геометрически это означает, что мы рассматриваем семейство прямых: m + 2ω = сonst
10.
На этом заканчиваетсяпервая часть курса.
Продолжение следует
2





 Менеджмент
Менеджмент








