Третий признак равенства треугольников

1.

Третий признак равенства
треугольников

2.

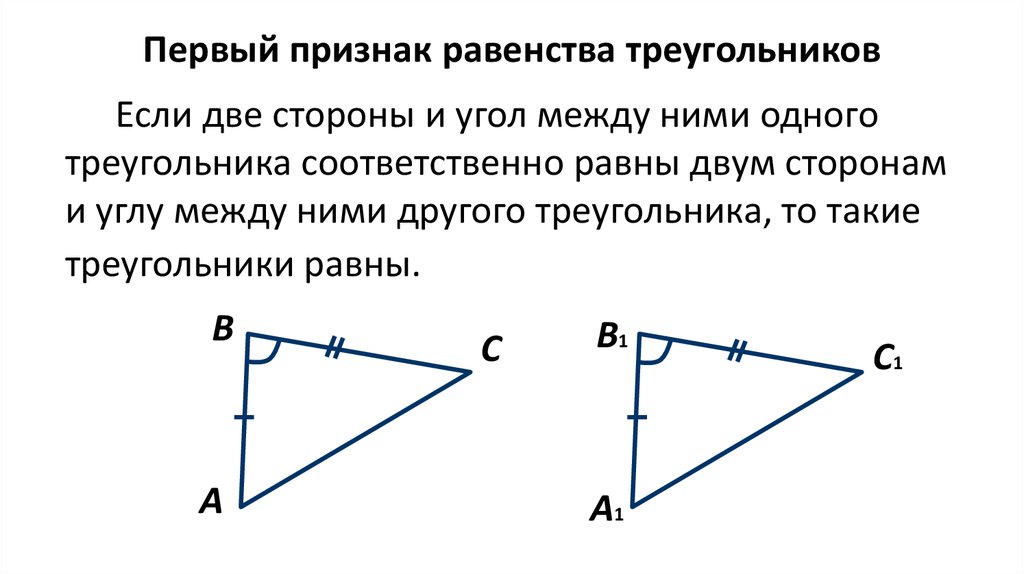
Первый признак равенства треугольников
Если две стороны и угол между ними одного
треугольника соответственно равны двум сторонам
и углу между ними другого треугольника, то такие
треугольники равны.
В
А
С
В1
А1
С1

3.

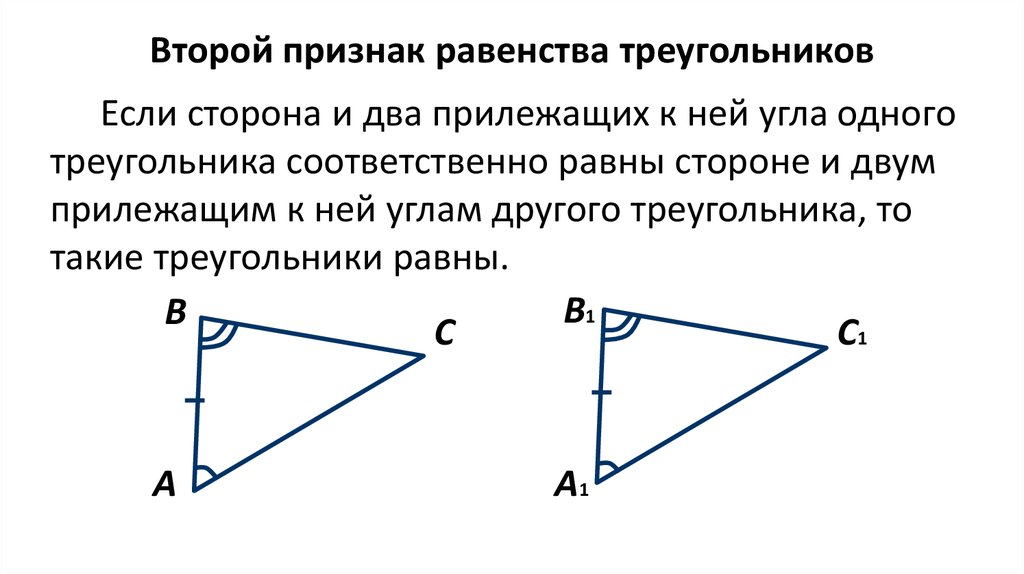
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного
треугольника соответственно равны стороне и двум
прилежащим к ней углам другого треугольника, то
такие треугольники равны.
В1
В
С
С1
А
А1

4.

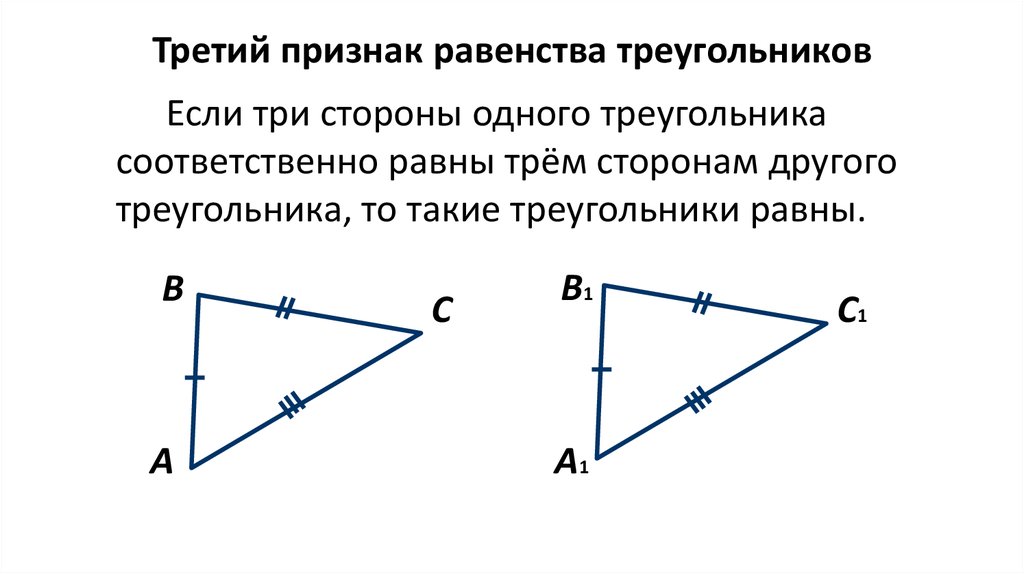
Третий признак равенства треугольников
Если три стороны одного треугольника
соответственно равны трём сторонам другого
треугольника, то такие треугольники равны.
В
А
С
В1
А1
С1

5.

Доказательство.
Пусть АВ = А1В1,
ВС = В1С1,
А
СА = С1А1.
1) ∆ А1С1С, ∆ В1С1С –
равнобедренные. А1
∠ 1 = ∠ 2, ∠ 3 = ∠ 4.
∠ А1СВ1 = ∠ А1С1В1.
∆ АВС = ∆ А1В1С1 (по первому признаку).
С
1 3
В
В1
2 4
С1

6.

А1 (А)
2) АС = А1С1,
∆ СА1С1 – равнобедренный.
∠ С = ∠ С1.
∆ АВС = ∆ А1В1С1 (по первому признаку).
С
С1
В1 (В)

7.

3) ∆ СА1С1, ∆ СВ1С1 – равнобедренные.
∠ 1 = ∠ 2,
∠ 3 = ∠ 4.
С
1
3
А1 (А)
∠ С = ∠ С1.
∆ АВС = ∆ А1В1С1
(по первому признаку).
Теорема доказана.
В1 (В)
2
4
С1

8.

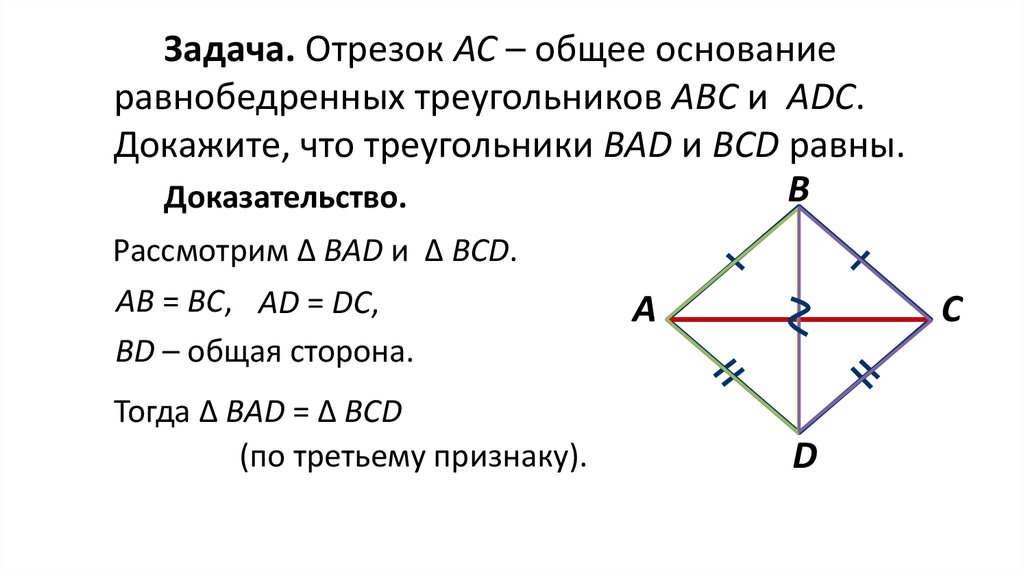
Задача. Отрезок АС – общее основание
равнобедренных треугольников АВС и АDC.
Докажите, что треугольники BAD и BCD равны.
В
Доказательство.
Рассмотрим ∆ BAD и ∆ ВСD.
АB = BС, АD = DС,
BD – общая сторона.
Тогда ∆ BAD = ∆ ВСD
(по третьему признаку).
А
С
D

9.

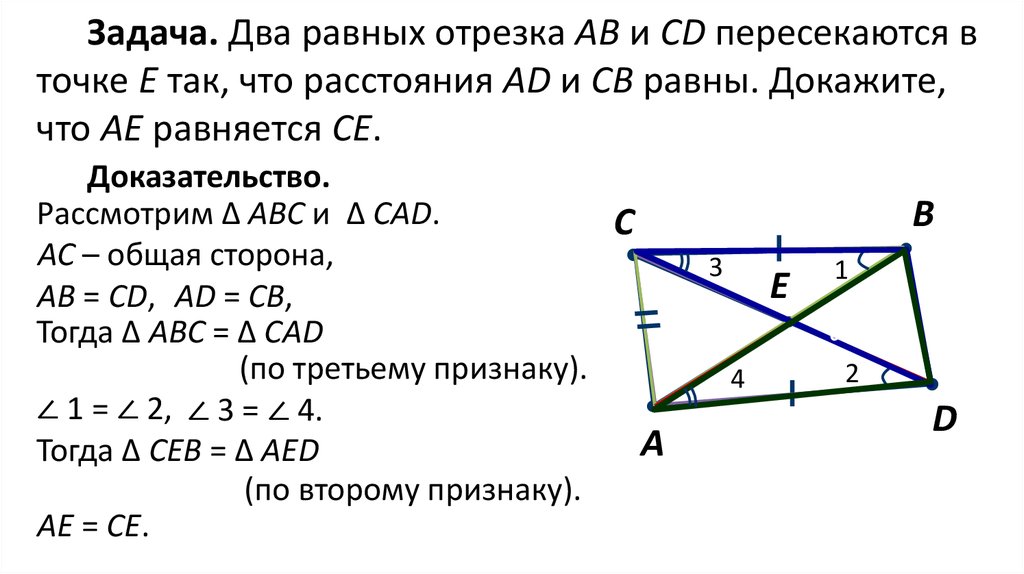
Задача. Два равных отрезка АВ и CD пересекаются в
точке Е так, что расстояния AD и СВ равны. Докажите,
что АЕ равняется СЕ.
Доказательство.
Рассмотрим ∆ АВС и ∆ САD.
С
АС – общая сторона,
АВ = СD, АD = СВ,
Тогда ∆ AВС = ∆ САD
(по третьему признаку).
∠ 1 = ∠ 2, ∠ 3 = ∠ 4.
А
Тогда ∆ СЕВ = ∆ АЕD
(по второму признаку).
АЕ = СЕ.
В
3
Е
4
1
2
D

10.

Треугольник – жёсткая фигура.

11.

12.

Перемычка