Расчет электростатических полей в вакууме

1. ЭЛЕКТРОМАГНЕТИЗМ

Лекция «Расчет
электростатических полей в
вакууме»

2. Характеристики заряженных макротел

Для характеристики (непрерывного) распределения
заряда для макротел удобно пользоваться понятиями
объемной [Кл/м3], поверхностной [Кл/м2] и линейной
[Кл/м] плотности заряда:
q dq
lim
V 0 V
dV
q dV
q dq
lim
S 0 S
dS
q dS
Δq dq
τ lim
Δl 0 Δl
dl
q dl
q V
V
q s
S
l
q l

3. Расчет характеристик ЭП макротел в точке А в вакууме: случай 1, 2

Точка А лежит на продолжении оси стержня, на расстоянии а от
его ближайшего конца
dq dl
dr
dE
2 k 2
4 0 r
r
1
Для конечного стрежня
a l
dr
l
1 a l
E k 2 k k
a(a l )
r a
a r
dq
dr
d k
k
r
r
dr
a l
k
k ln
a
a r
a l
Для полубесконечно длинного стрежня
dr
1 k
E k 2 k
r a a
ar
dq

4. Расчет характеристик ЭП макротел в точке А в вакууме: случай 3

Точка А лежит на перпендикуляре к середине конечного равномерно
заряженного стержня длины l на расстоянии а от него dq dl
dq
dl
dq
dl
k
d k
k
dE
2
2
y
4
r
r
r
r
dEy
0
a
rd
x
r
dl
A
cos
cos
dEx
dl
rd
d
d
dE
k
k
k
k
r cos
a
r2
r 2 cos
d
dEx dE sin
r rd a
d k
cos
dE y dE cos
rd
2
k
k
E
sin
d
(cos 1 cos 2 )
dl
x
a
a
l
12
k
k
Ey
cos d (sin 2 sin 1 )
a
a
2
d
1
2
1
2
2
k
k ln tg ln tg
E
E
E
x
y
cos
2 4
2 4
dE
1
1

5. Расчет характеристик ЭП макротел в точке А в вакууме: случай 4

Точка А лежит на перпендикуляре к середине бесконечного равномерно
заряженного стержня на расстоянии а от него E E 2 E 2
x
y
dE
y
x
dEy
A
dEx
r rd a
rd
dl
l
Ex
Ey
k
a
k
a
2
sin d
1
2
k
(cos 1 cos 2 )
a
cos d
1
k
(sin 2 sin 1 )
a
k / 2
k
E р 2 dE y 2
sin
d
2
(cos 1 cos 2 )
a 0
a
0
/2
2
k
k
(1 0) 2
a
a
l 1 0
2

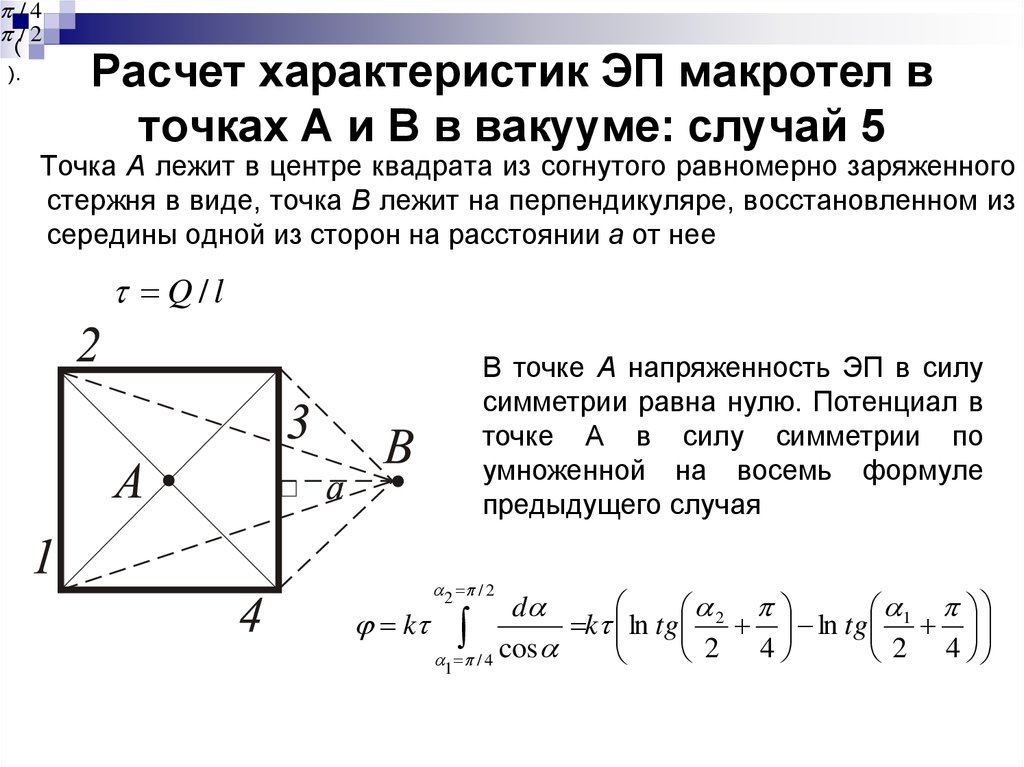
6. Расчет характеристик ЭП макротел в точках А и В в вакууме: случай 5

/4
(/ 2
).
Расчет характеристик ЭП макротел в
точках А и В в вакууме: случай 5
Точка А лежит в центре квадрата из согнутого равномерно заряженного
стержня в виде, точка В лежит на перпендикуляре, восстановленном из
середины одной из сторон на расстоянии а от нее
Q/l
В точке А напряженность ЭП в силу
симметрии равна нулю. Потенциал в
точке А в силу симметрии по
умноженной на восемь формуле
предыдущего случая
k
2 / 2
d
2
1
k
ln
tg
ln
tg
2 4
2 4
1 / 4 cos

7. Расчет характеристик ЭП макротел в точках А и В в вакууме: случай 5

/4
(/ 2
).
Расчет характеристик ЭП макротел в
точках А и В в вакууме: случай 5
Точка А лежит в центре квадрата из согнутого равномерно заряженного
стержня в виде, точка В лежит на перпендикуляре, восстановленном из
середины одной из сторон на расстоянии а от нее
Q/l
В точке В напряженность находится по принципу
векторного
сложения
напряженностей
ЭП,
создаваемых каждым из стержней 1 и 3 отдельно,
согласно изложенной выше методике (см. рис. 2,
случай 3); для стержней 2 и 4 суммируются только
составляющие
вдоль
направления
АВ,
составляющие же напряженности,
расположенные перпендикулярно направлению АВ, компенсируют друг
друга в силу симметрии расположения стержней 2 и 4. Далее суммируем
полученные для всех стержней результаты вдоль направления АВ.
Потенциал находится как алгебраическая сумма потенциалов,
создаваемых каждым из стержней 1, 2, 3, 4 по формуле как для конечного
стрежня (предыдущий случай – случай 3) с учетом соответствующих углов
(пределов интегрирования).

8. Расчет характеристик ЭП макротел в точке А в вакууме: случай 6

Точка А лежит в центре кривизны дуги радиусом R из равномерно
заряженной тонкая нить, длина нити 1/n от длины окружности
dq dl
dE
1
4 0
dq
dl
k
r2
r2
dEx dE sin
d k
dE y dE cos
dq
dl
k
r
r
E Ex2 E y2
В силу симметрии векторная сумма (интеграл)
всех составляющих
dEx
будет равна нулю
k / n
k
E р 2 dE y 2
cos d 2 sin
R 0
R
n
0
/n
k
R
k 2 R 2 k
dl
R n
n
0
2 R / n

9. Расчет характеристик ЭП макротел в точке А в вакууме: случай 7

Точка А лежит на перпендикуляре к центру кольца, на расстоянии а от
его плоскости
dE
1
4 0
dq
dl
k
r2
r2
dEx dE sin
dE y dE cos
E Ex2 E y2
dq
dl Аналогично случаю 3 (4) и в силу симметрии для
d k
k
напряженности находим лишь интеграл
r
r
2 R
2 R
k
E р dE y 2
cos dl
2
R a
0
0
2 k aR
R
2
a
2 3
.
В силу симметрии векторная сумма (интеграл)
всех составляющих
dq dl
dEx
k
R2 a2
будет равна нулю
2 R
dl
0
2 Rk
R2 a2

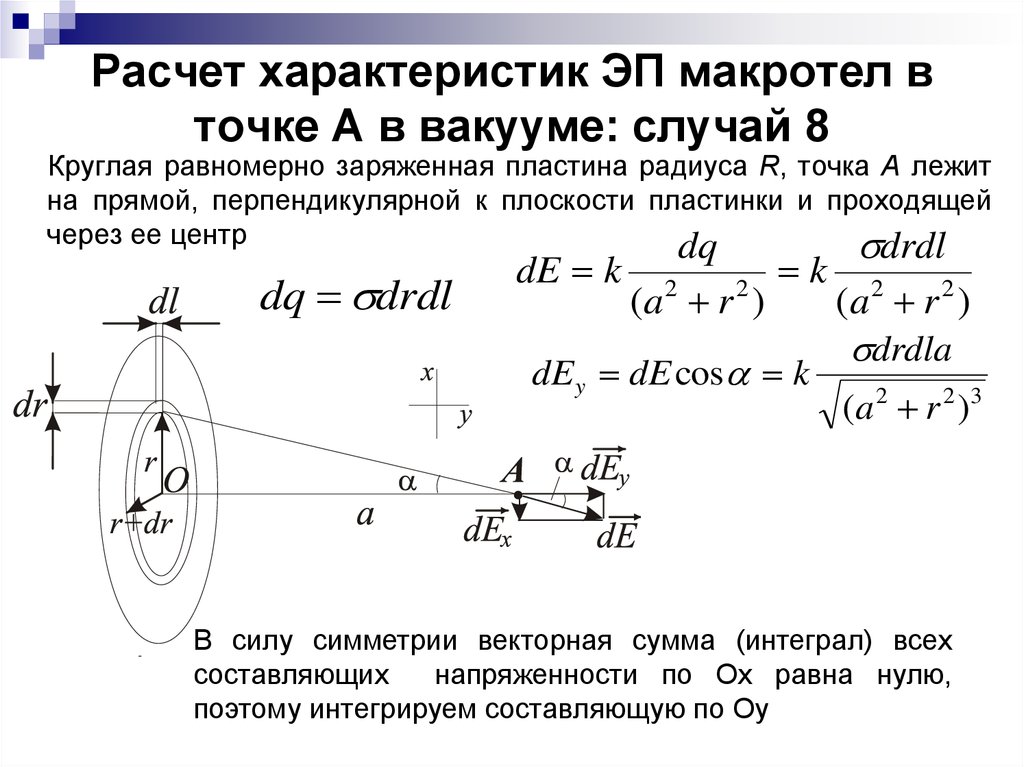
10. Расчет характеристик ЭП макротел в точке А в вакууме: случай 8

Круглая равномерно заряженная пластина радиуса R, точка А лежит
на прямой, перпендикулярной к плоскости пластинки и проходящей
через ее центр
dq
drdl
dq drdl
dE k
(a r )
2
2
k
dEy dE cos k
(a 2 r 2 )
drdla
( a 2 r 2 )3
В силу симметрии векторная сумма (интеграл) всех
составляющих
напряженности по Ох равна нулю,
поэтому интегрируем составляющую по Оу

11. Расчет характеристик ЭП макротел в точке А в вакууме: случай 8

Круглая равномерно заряженная пластина радиуса R, точка А лежит
на прямой, перпендикулярной к плоскости пластинки и проходящей
через ее центр
a r x
dx
ak
E y 2 ak
3
/
2
2
2 3
0 (a r )
a2 x
2rdr dx
R
2
rdr
2 ak x
1 / 2
2
a2 R2
1
1
2 ak
2
2
a R
a2 R2
a
a2
a
1
1
1
2
2
2 0
a R 2 0
R2
1 2
a

12. Теорема Остроградского-Гаусса

Потоком вектора Е называется произведение
(dS dS n )
d E En dS E dS
Вычисление напряженности и потенциала электростатического
поля заряженных макротел, проведенное выше с помощью
интегралов, в ряде случаев может быть заменено на более простое
вычисление тех же характеристик с
помощью теоремы
Остроградского-Гаусса.
Теорема Остроградского–Гаусса для
электростатического поля в вакууме:
поток
вектора
напряженности
электрического
поля
через
произвольную замкнутую поверхность
равен
алгебраической
сумме
охватываемых поверхностью зарядов,
деленной
на
электрическую
постоянную ε0
E E dS
S
E E dS
S
1
q
0
dV
0 V

13. Расчет характеристик ЭП макротел с помощью теоремы Остроградского-Гаусса: случай 1

Расчет характеристик ЭП макротел с
помощью теоремы ОстроградскогоГаусса: случай 1
Случай бесконечного равномерно заряженного тонкого стержня (нити,
проволоки, цилиндра радиусом R). Замкнутой поверхностью
простейшей формы, охватывающей все заряженное тело, является
цилиндр радиуса r>R.
E E dS
q
0
E 2 rl l / 0
S
E
,r R
2 0 r
2
r2 dr
q
r2
2 1 E dr
ln
2 0 r1 r
2 0 h r1
1

14. Расчет характеристик ЭП макротел с помощью теоремы Остроградского-Гаусса: случай 2 (3)

Случай бесконечной равномерно заряженной плоскости или пластины
(двух пластин – конденсатора). Замкнутой поверхностью простейшей
формы, охватывающей всю плоскость, является параллелепипед с
основанием «плоскость» и высотой b 0
E
E 2S S / 0
E E dS
2 0
0
S
x
" " x 0,
2 1 Edx
x,
2 0 " " x 0.
0
q
Для поля между пластин
1
1 2 ,
E E1 E2
2 0
1 2 , E
(0), x 0,
( x) (0) x ( 0 ),0 x d ,
(0) x , x d .
0
0
(0) – потенциал
самой
плоскости.

15. Расчет характеристик ЭП макротел с помощью теоремы Остроградского-Гаусса: случай 4, 5

4. Случай равномерно заряженного по объему шара радиуса R
(суммарный заряд Q). Замкнутой поверхностью простейшей формы,
охватывающей весь шар, является сфера радиусом r≥R
E E dS
S
E
Q
4 0 r
2
,r R
q
0
(1)
4
E 4 r 2 R3 / 0 Q / 0
3
dV
dE
,r R
(2)
2
4 0 r
5. Случай равномерно заряженной по поверхности сферы радиусом R
(суммарный заряд Q). Замкнутой поверхностью простейшей формы,
охватывающей всю сферу, является сфера радиусом r≥R. Для поля
вне сферы справедлива формула (1). Внутри сферы напряженность
ЭП равна нулю, так как нет охватываемых поверхностью
электрических зарядов.

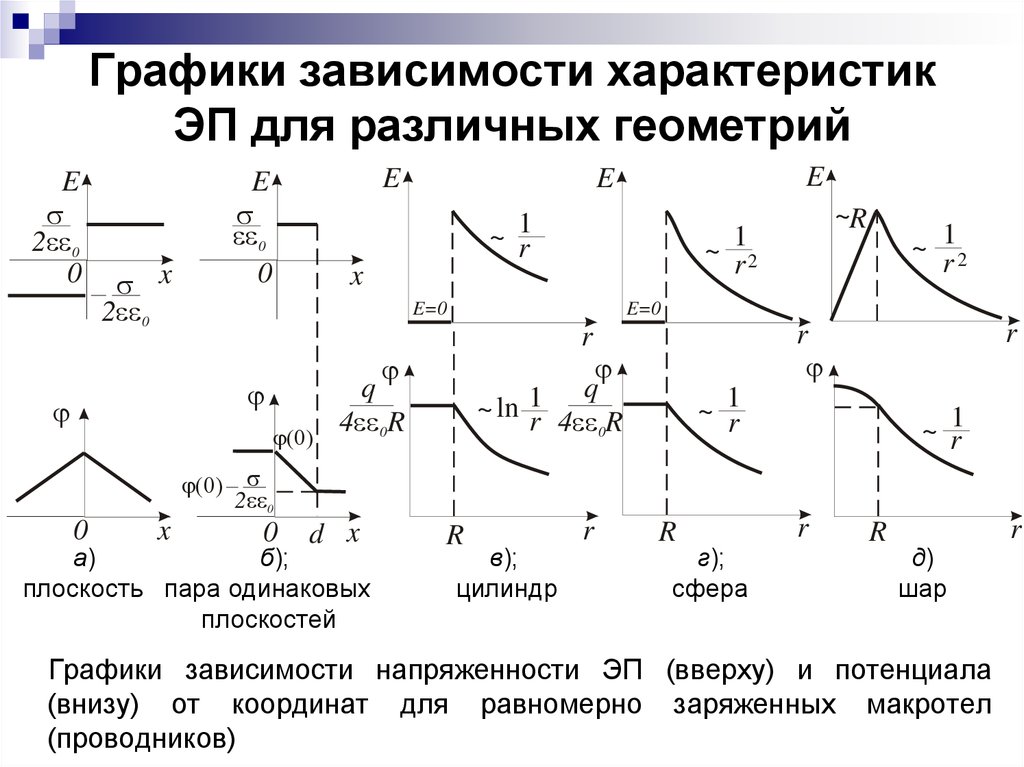
16. Графики зависимости характеристик ЭП для различных геометрий

E
2 0
0
E
E
0
0
x
2 0
~ 1r
x
0
x
~R
~ 12
r
E=0
E
E
~ 12
r
E=0
q
~ ln 1r 4 R
0
q
4 0R
r
r
r
~ 1r
~ r1
2 0
0
d x
а)
б);
плоскость пара одинаковых
плоскостей
R
в);
цилиндр
r
R
г);
сфера
r
R
д)
шар
Графики зависимости напряженности ЭП (вверху) и потенциала
(внизу) от координат для равномерно заряженных макротел
(проводников)
r

17. Благодарю за внимание