Похожие презентации:
Принцип суперпозиции электростатических полей. Примеры расчета полей
1. Глава 3 Электричество и магнетизм
§ 2. Принцип суперпозицииэлектростатических
полей.
Примеры расчета полей.
Глава 3
Электричество и магнетизм
2.
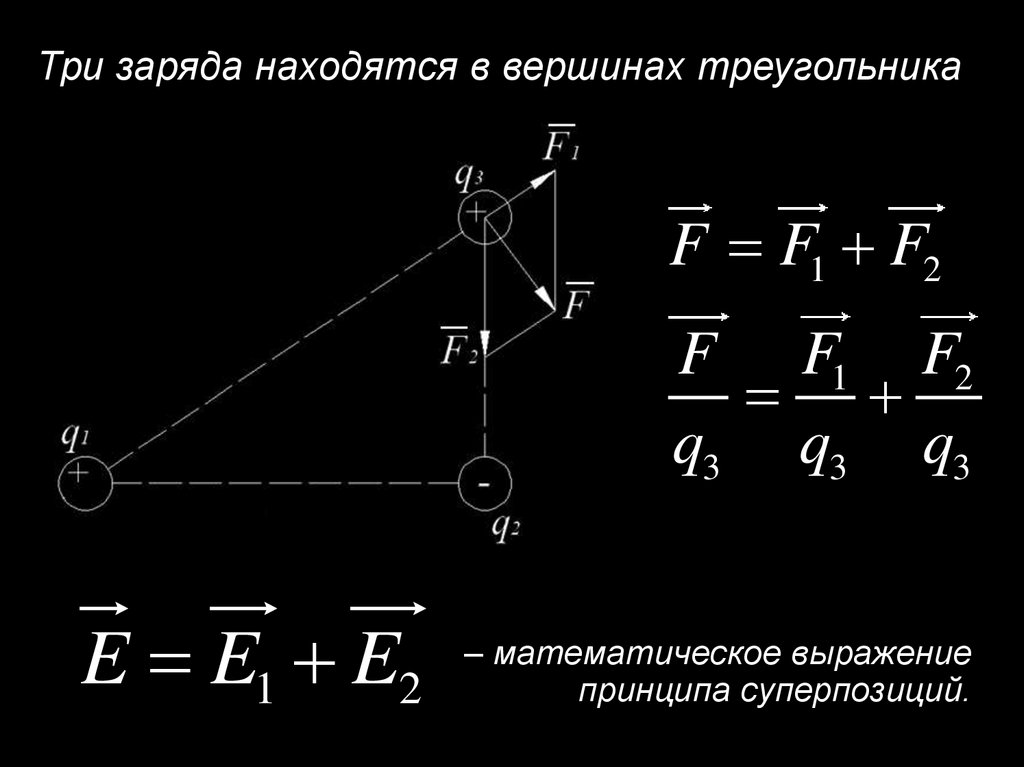
Три заряда находятся в вершинах треугольникаF F1 F2
F F1 F2
q3 q3 q3
E E1 E2
– математическое выражение
принципа суперпозиций.
3.
nE Ei
i 1
Принцип суперпозиции: напряженность
электрического поля системы зарядов
равна векторной сумме напряженностей
полей создаваемых каждым зарядом в
отдельности.
4. Принцип суперпозиции в интегральной форме:
Напряженность поля элементарногоопределяется выражением:
заряда
dq r
rdq
dE k 2 k 3
r r
r
Принцип суперпозиции в интегральной форме:
rdq
E k 3
r
Q
5.
Можно выделить следующие видыраспределения электрических
зарядов: линейное, плоское, объемное.
Линейная плотность заряда
dq
dl
Поверхностная плотность заряда
Объемная плотность заряда
dq
dS
dq
dV
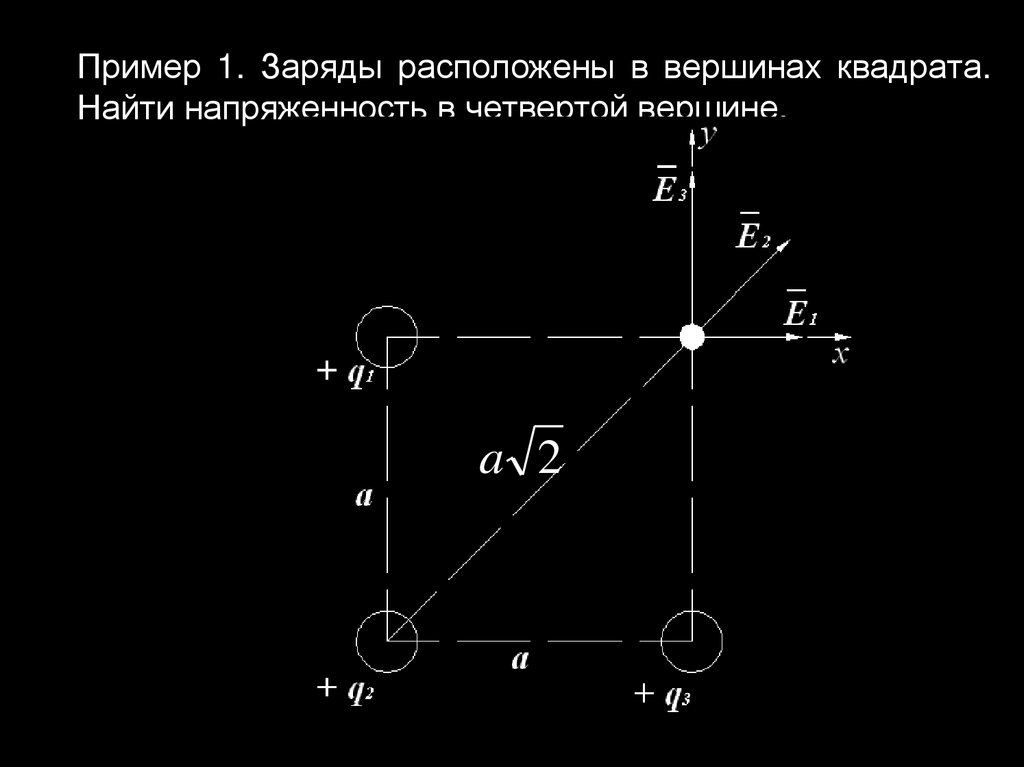
6. Пример 1. Заряды расположены в вершинах квадрата. Найти напряженность в четвертой вершине.
a 27.
E Ex E yE E E
2
x
2
y
(1)
Ex E1 E2 cos 45
E y E3 E2 cos 45
8. Напряженности полей зарядов в вершине квадрата:
q2q1
q3
E2 k
E1 k 2
E3 k 2
2
a
a
a 2
Проекция напряженности на ось ОХ:
q1
q2
Ex E1 E2 cos 45 k 2 k
a
a 2
k
2
2 q1 q2
a
4
2
2
2
9.
Проекция напряженности на ось ОУ:q3
q2
E y E3 E2 cos 45 k 2 k
a
a 2
2
k
2
2 q3 q2
a
4
Находим искомую напряженность (1).
2
2
10. Пример 2: Заряд q распределен по стержню длиной b, найти напряженность в точке на расстоянии а от его конца.
dqdE k 2
r
dq dr
dE k
dr
r
2
11.
Интегрируя понапряженность:
a b
E
k
a
dr
r
2
длине
k
r
a b
a
стержня,
находим
1
1
k
a a b
b
kq
k
a ( a b) a ( a b)
12. Пример 3. Определить напряженность на расстоянии а от заряженного проводника.
dq dldq
dE k 2
r
dE x k
dl
r
2
sin
dl sin rd
13. Записываем дифференциальное выражение для напряженности и интегрируем по углу:
dEx kk
d
r
dl
r
2
sin k
k
rd
sin d
a
r
2
14.
2Ex
1
k sin
k cos
d
a
a
k
(cos 1 cos 2 )
a
2
1
15. Проекция напряженности на ось ОУ
Ey2
1
k cos
k sin
d
a
a
2
1
k
(sin 1 sin 2 )
a
Напряженность рассчитываем по формуле:
E E E
2
x
2
y
16. Для бесконечной заряженной нити напряженность равна:
Длябесконечной
напряженность равна:
заряженной
нити
k
k
E (cos 0 cos ) 2
a
a
2 0 a
E
2 0 a
17. Пример 4. Поле на оси тонкого кольца перпендикулярно его плоскости.
++
+
+
R
dl
+
r
+
+
+
+
+
+
+
x
dE
18.
Поле, создаваемое на оси зарядомэлемента длины кольца, вычисляется:
dq
dl
dE k 2 k
2
2
2
r
R x
19.
Берем только проекцию на ось Х:dEx k
dl
cos
2
R x
dl
x
k xdl
k 2
3/2
2
2
2
2
2
R x R x
R x
2
20. Интегрируем полученное выражение по длине кольца:
E x dE xl
R
k x
2
x
2 3/ 2
l
R
q 2 R
Ex
R
kxq
2
x
2 3/2
k x
2
x
2 3/ 2
2 R
21. Полученное соотношение, можно использовать, например для нахождения напряженности поля кольца с внутренним и внешним радиусом.
dSdR
dS 2 RdR
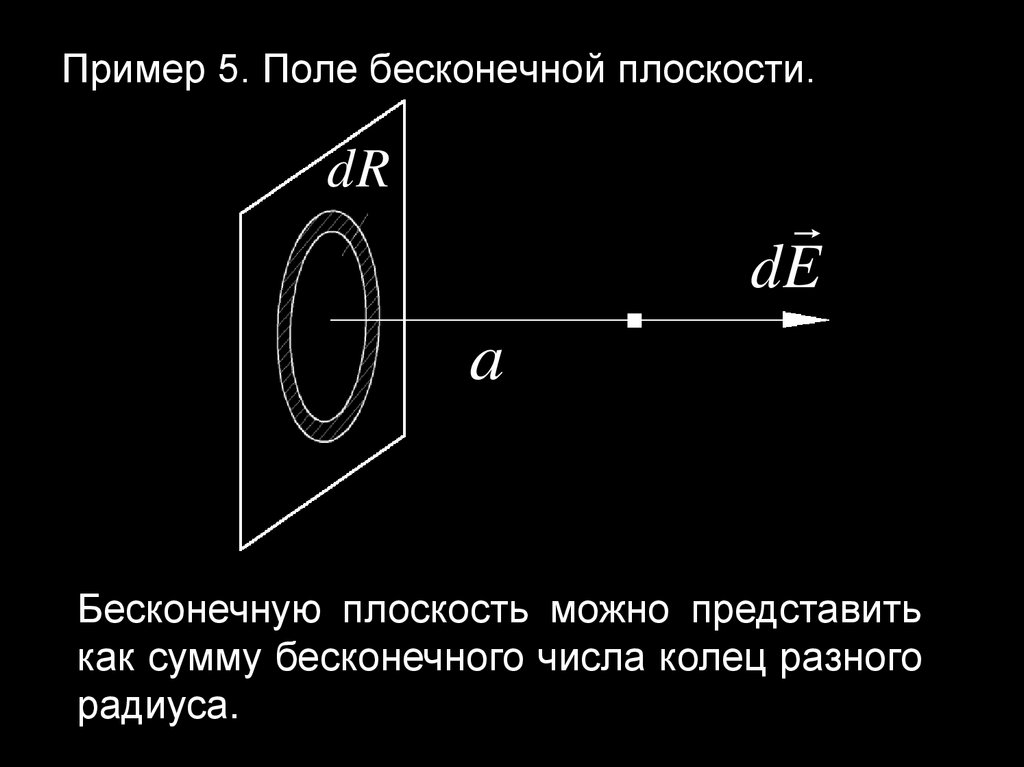
22. Пример 5. Поле бесконечной плоскости.
dRa
.
dE
Бесконечную плоскость можно представить
как сумму бесконечного числа колец разного
радиуса.
23.
kadqka dS
dE 2
2 3/2
2
2 3/2
(R a )
(R a )
ka 2 RdR
dE 2
2 3/ 2
(R a )
24.
E0
ka 2 RdR
R
2
a
2 3/2
ka
0
d R a
2
R
2
a
2
2 3/2
Поле бесконечной плоскости является
однородным.
E
2 0
2 0











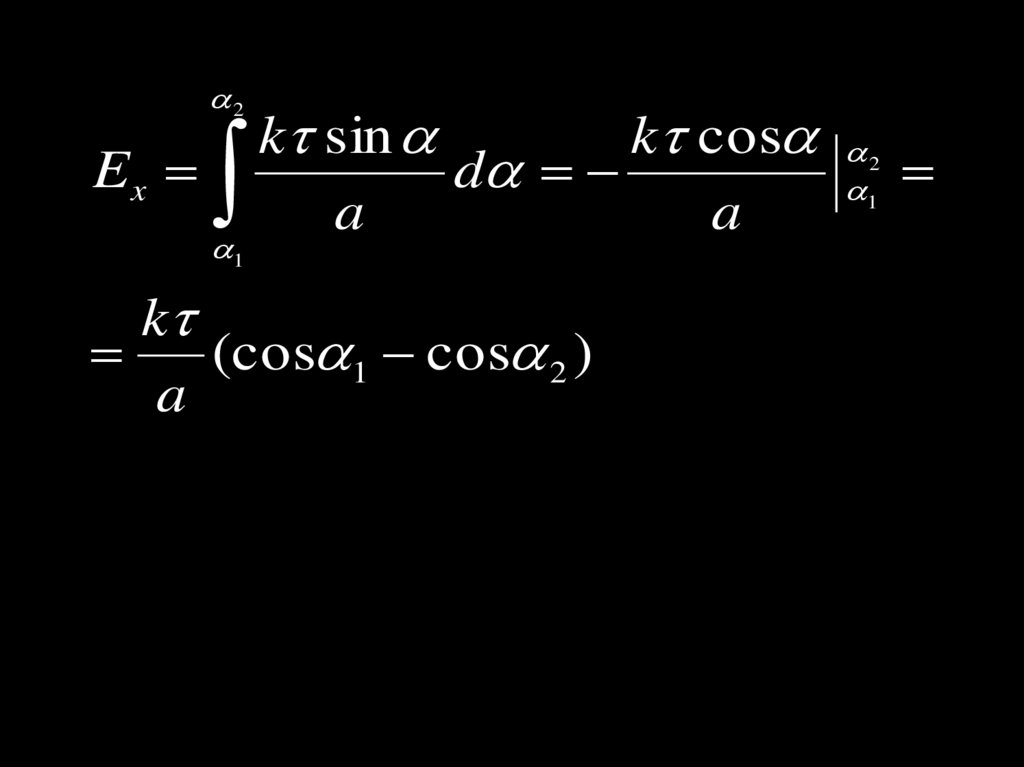







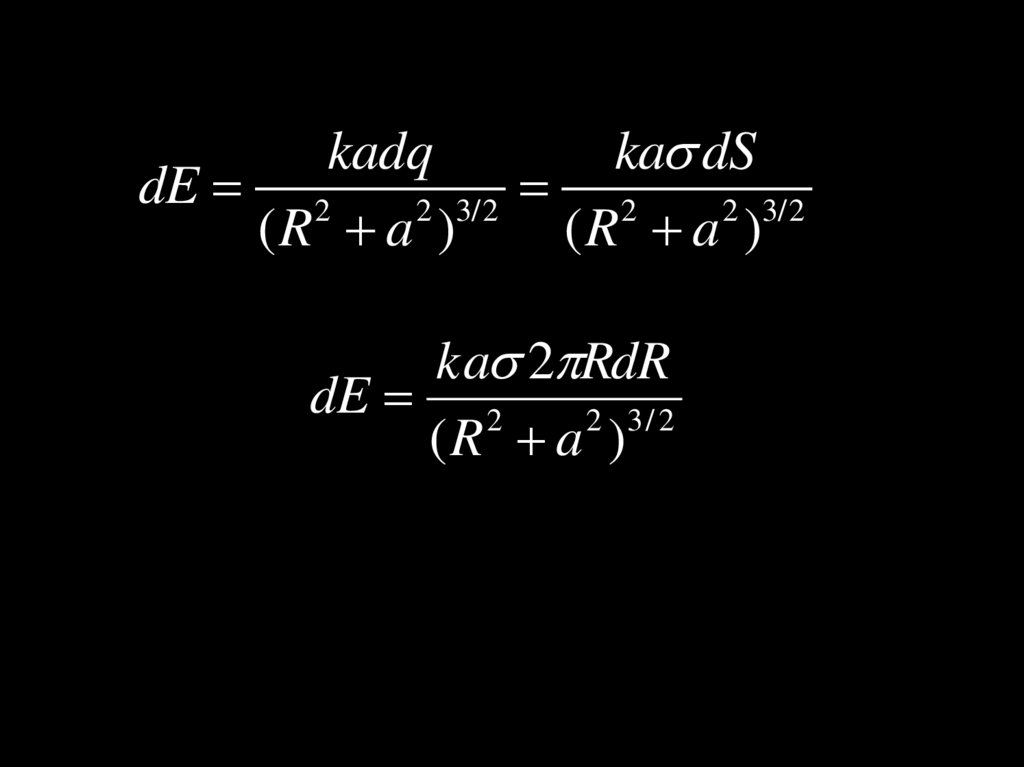

 Физика
Физика








