Похожие презентации:
Модели радиолокационных сигналов
1.
Модели радиолокационных сигналов1. Детерминированный сигнал.
2. Сигнал со случайной начальной фазой.
3.Сигнал со случайной начальной фазой и флуктуирующей амплитудой.
y (t ) u (t ) n (t )
y (t ) U m (t , ) n (t )
u(t , ) U m cos[ 0t (t ) ] w( ) 1 / 2
u (t , ) U m cos[ 0t (t ) ] w( ) 1 / 2
w( )
e
2
2
2
2.
Синтез оптимальных обнаружителей сигналовI. Обнаружение одиночного радиоимпульса с полностью известными параметрами на фоне
белого шума. Единственное, что предполагается заранее неизвестным, это сам факт
наличия сигнала
y (t ) u (t ) n(t )
M {n(t )} 0;
G ( )
0;1
R ( ) M {n(t ) n(t )}
R ( ) exp( j ) d
2 N0 f KШ kT0 f
N0
( )
2
N0
.
2
KШ Ta / T0 Tпр / T0 1
T0=290°K , kT0= 4 ·10-21
По гипотезе H 0
y (t ) n(t )
а по гипотезе H 1
y (t ) u (t ) n(t )
Тогда n(t ) y (t ) u (t )
3.
( y ) отношение правдоподобияN 0 ( Fmax
2
n
1
1
Fmin ) t
dt
2 Fmax
T
N
1
2
n
n
(t )dt
2
n i 1
N0 0
2
i
w[n 2 (t )] ( 2 n2 ) N
T
1
2
2
exp
n (t )dt H 0
N0 0
w[n (t )] ( 2 )
T
1
2
2
exp
[ y (t ) u (t )] dt H1
N0 0
2
2 N
n
4.
1 T 2[ y (t )] exp
[u (t ) 2u (t ) y (t )]dt
N0 0
T
2
u
(t )dt Э ;
0
T
u(t ) y (t )dt R
uy
( 0)
0
Э
[ y (t )] exp
2 Ruy (0) / N 0
N0
Э
2 Ruy (0) / N 0 ln l0 ; Ruy (0) N 0 / 2 ln l0 Э/2
N0
5.
y(t)Х
u(t)
Решающее
устройство
l0
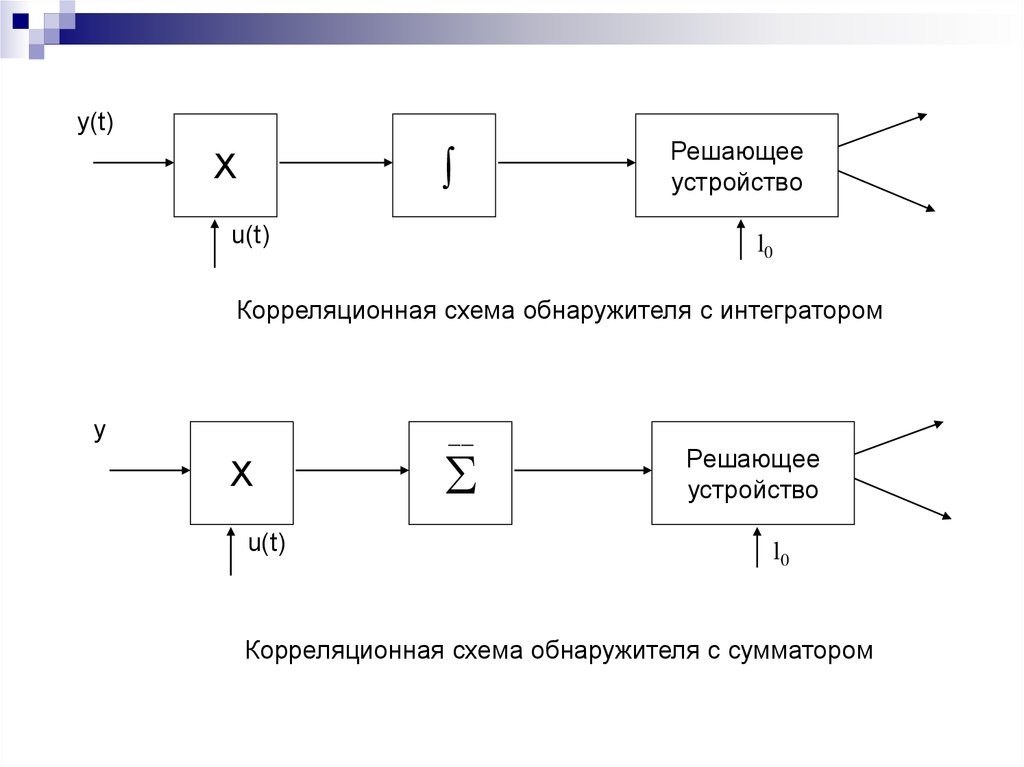
Корреляционная схема обнаружителя с интегратором
y
__
Х
u(t)
Решающее
устройство
l0
Корреляционная схема обнаружителя с сумматором
6.
В оптимальном приёмнике независимо от выбранного критерия должнывыполняться следующие операции
а) входное напряжение приёмника uвх(t) нужно перемножить с опорным
напряжением uоп(t), представляющим собой копию излученных передатчиком РЛС
колебаний;
б) результат перемножения следует интегрировать за время существования
сигнала τс;
в) выходное напряжение интегратора необходимо сравнивать с некоторым
постоянным напряжением, именуемым пороговым или просто порогом Uпор.
;
сравнивается с пороговым напряжением Uпор: если Uвых>Uпор, то принимается
решение о наличии сигнала, и с вероятностью D это будет соответствовать
действительности; при Uвых<Uпор считают, что сигнала нет и это соответствует
действительному положению с вероятностью F.
7.
D)Определим вероятности ошибочных решений (F и
Дисперсия на выходе коррелятора или согласованного фильтра
T
T
0
0
u (t )dt Rn (t )u (t )d
2
x
x2
N0
Rn (t )
( )
2
N0
Э
2
Следовательно, ФПРВ выходного шума имеет вид
1
exp xш2 /( N 0 Э
N 0 Э
w( xш )
1
1 Ф(q1 )
2
F
exp xш /( N 0 Э dx
2
N 0 Э l0
где q1 l0 / N 0 Э относительный порог
Ф(z)
2
z
2
exp
d интеграл вероятности
0
8.
Для смеси сигнала с шумомT
M ( xсш вых ) M[u вых (t) n вых (t)] M[u вых (t) n вых (t) u вых (t)]dt
0
T
T
0
0
2
u
(t)dt Э , т.к. M[n вых (t) u вых (t)]dt 0
w( xсш )
D
1
N 0 Э
exp ( xсш Э) 2 /( N 0 Э
1 Ф(q 2 / 2 - q1 )
exp ( xсш Э ) /( N 0 Э dx
2
N 0 Э l0
1
2
где q1 l ' 0 / N 0 Э относитель ный порог
q 2 2Э / N 0
отношение сигнал - шум на выходе
Пороговый сигнал определяется как минимальное отношение сигнал-шум, при котором
сигнал обнаруживается с заданными вероятностями D и F .
9.
Обнаружение сигнала со случайными параметрамиY (t ) u(t , 1 , 2 ,.., n ) n(t )
Модель сигнала со случайными параметрами
1, … n – случайные неизмеряемые параметры сигналов. ОП - (y)
определим, используя сведение сложной гипотезы к простой, т.е.
( y ) ... ( y, 1 , 2 ,...) W ( 1 , 2 ,...)d 1...d n
W ( 1 , 2 ,...) W ( 1 )W ( 2 )..W ( n )
Сигнал с неизвестной начальной фазой u(t)
= u(t, ) = U(t)cos(w0t + )
Пусть W( ). – закон распределения фазы.
Если фаза распределена равномерно на промежутке [- ; ] или [0; 2 ], то
W( ) = 1/2 ....
10.
T( y , )
k exp{ 1 / N 0 [ y (t ) u (t , )]2 dt}
0
T
k exp{ 1 / N 0 y 2 (t )dt}
0
T
T
0
0
exp{ 1 / N 0 u 2 (t , )dt 2 / N 0 y (t ) u (t , )dt}
I1
2I 2
exp{
}
N0
N0
T
T
0
0
I1 u 2 (t , )dt U 2 (t ) cos 2 ( 0t )dt
T
T
0
0
1 / 2 U 2 (t )dt 1 / 2 U 2 (t ) cos( 2 0t 2 )dt Э
11.
TI1'
1
U 2 (t )dt
20
T
1
2
I U (t ) cos( 2 0t 2 )dt
20
''
1
Т.к. I >> I , то используя метод «стационарной фазы» получим
T
T
0
0
I 2 y (t ) u(t , ) y (t ) U (t ) cos( 0 t )dt
T
T
0
0
cos y (t ) U (t ) cos 0t dt sin y (t ) U (t ) sin 0t dt
I 2 x1 cos y1 sin z cos( )
12.
z2
x1
y1
arg
x1
2
y1
( y (t ), ) exp{ Ý/N0 2 z cos( ) / N 0 }
( y (t )) [ y (t ), ] ( )d ( ) 1 / 2
,
2
2
2 z cos( )
1 / 2 [ y (t ), ]d 1 / 2 exp{-Ý/N0
}d
N0
0
0
2z
exp( Ý/N0 ) I 0 ( )
N0
где I0(2z/N0) – функция Бесселя первого рода, нулевого порядка
13.
Характеристики обнаруженияZш – распределение шума, Zсш – распределение смеси сигнала и шума.
Модуль вектора Z определяется составляющими х1ш и х2ш, которые
представляют собой независимые случайные величины, распределенные по
закону Релея.
Математическое ожидание составляющих x и y равно 0.
Дисперсия шума:
N 0Эс / 2
2
ш
1
( z )
e
N 0Э
2
ш
Z ш2
N 0Э
1
F ( z )dz
e
N 0Э
U0
U0
2
ш
2
ш
Z ш2
N 0Э
dzш2 e l2
14.
U0l2
U 0 l2 N 0 Э
N 0Э
U0
1
ln F l2
U 0 N 0Э lnF N 0Э ln
N 0Э
F
Модуль Zсш будет распределен по закону Релея (Релея – Райса)
( Z сш )
Z сш
2
сш
exp{
Z
2
сш
Z )
2
2
c
2
c
} I0 (
2
2 Z сш
Z сш
Э2
2Zcш
exp{
} I0 (
)
2
N 0Э
N 0Э
N0
Z сш Zc
2
)
15.
D2
2
(
Z
)
d
z
сш
cш
U0
X
сш
)d Z сш
U0
N 0 Э ln(1/F )
( Z
2
2
2 Z сш
zсш
Э2
2 Z сш
exp{
} I0 (
)dZ сш
N 0Э
N 0Э
N0
e
X 22 q22
2
I 0 ( q2 x2 )dx2
N 0 Э ln(1/F )
Zс
2E
q2
N0
Характеристика обнаружения D(q2) по сравнению
со
случаем
известной
начальной
фазы
смещается вправо.
Это связано с тем, что при неизвестной
начальной фазе для обеспечения эквивалентного
значения вероятности правильного обнаружения
(по сравнению со случаем известных параметров
сигнала) необходимо более высокое отношение
с-ш.
16.
Обнаружение сигнала со случайной амплитудойи случайной начальной фазой
U(t) = AU(t)cos( 0t + ), 0…2 , ( ) = 1/2 .
U(t) в отличие от случайного сигнала с известными параметрами
является статистически усредненной по большому числу реализаций.
А – случайная величина, распределенная по закону Релея.
N0
Z2
( y )
exp{
}
N 0 Эср
N 0 ( N 0 Эср )
17.
Структура обнаружителя аналогична варианту со случайной начальной фазой,Отличие в величине порога обнаружения:
U0
N 0 Эср
Дисперсия смеси сигнала с шумом
2
сш
с2 ш2 ш2 (1 с2 / ш2 ) ш2 (1 q 2 )
с2
Эср
2
N
ш2 0
2
Условие равенства энергий
2
Эср / 2
2
с
q 2
Эср / N 0
ш N0 / 2
2
Z сш
)
1
w ( Z ) 2 exp{ 2 }
2 сш
2 cш
2
сш
D w ( Z )dZ
2
сш
2
сш
U0
U0
F exp{
}
N 0 Ý ñð
U0
U0
exp 2 exp
2 сш
N 0 Эср (1 q2 )
1
D F
1 q2
18.
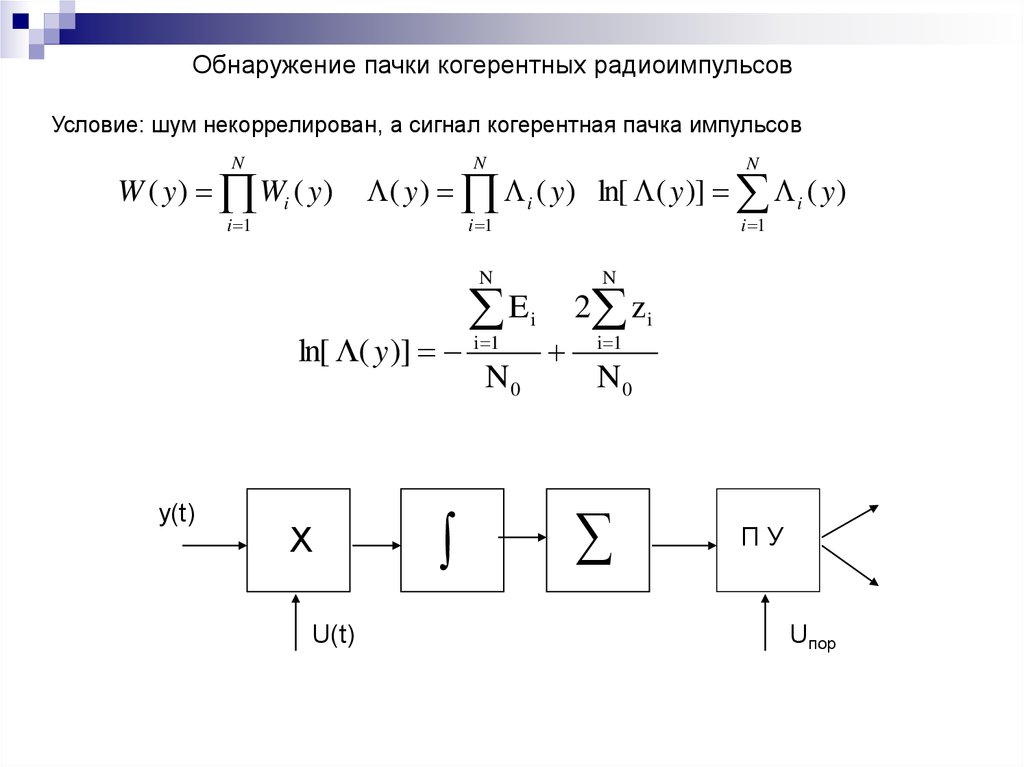
Обнаружение пачки когерентных радиоимпульсовУсловие: шум некоррелирован, а сигнал когерентная пачка импульсов
N
W ( y ) Wi ( y )
i 1
N
N
i 1
i 1
( y ) i ( y ) ln[ ( y )] i ( y )
N
ln[ ( y )]
y(t)
Х
U(t)
E
i 1
N0
N
i
2 z i
i 1
N0
ПУ
Uпор
19.
y(t)СД
УПЧ
АД
ФСОП
ПУ
Uстр
Uпор
ГСИ
Структура обнаружителя пачки с неизвестной начальной фазой имеет 2 канала.
А обнаружитель сигнала со случайной начальной фазой и флуктуирурующей
амплитудой отличается аналогично как и для одиночного импульса.
Обнаружение некогерентных радиоимпульсов
y(t)
ОФ
КвД
ПУ
Uпор
20.
Оптимальная фильтрацияКритерии построения оптимального фильтра:
Минимума среднеквадратичной ошибки фильтрации (СКО).
Максимума отношения с/ш.
Максимума апостериорной вероятности.
Минимума дисперсии шума.
Т
z
Т
-1
z
W1
W0
-1
W2
x1
x2
y
x0
T
W x
21.
Ty
W
x
Сигнал на выходе фильтра
Мощность (дисперсия) на выходе фильтра
T
T
y 2 W T xxT W W T xx
W W R x W
Rx
y 2 x2вых Dxвых
R s Rп ш2 вх I
S2 вых W T R s W
22.
УРАВНЕНИЕ ДАЛЬНОСТИ РАДИОЛОКАЦИОННОГО ОБНАРУЖЕНИЯДальность действия РЛС в свободном пространстве
Дальностью действия радиолокационной станции называется наибольшее
расстояние между РЛС и целью, на котором ее обнаружение производится с заданными
вероятностями правильного обнаружения и ложной тревоги.
Дальность действия зависит от различных факторов: технических параметров
станции, характеристик цели, условий распространения радиоволн, наличия и уровня
различного рода помех и ряда других факторов, большинство из которых изменяется во
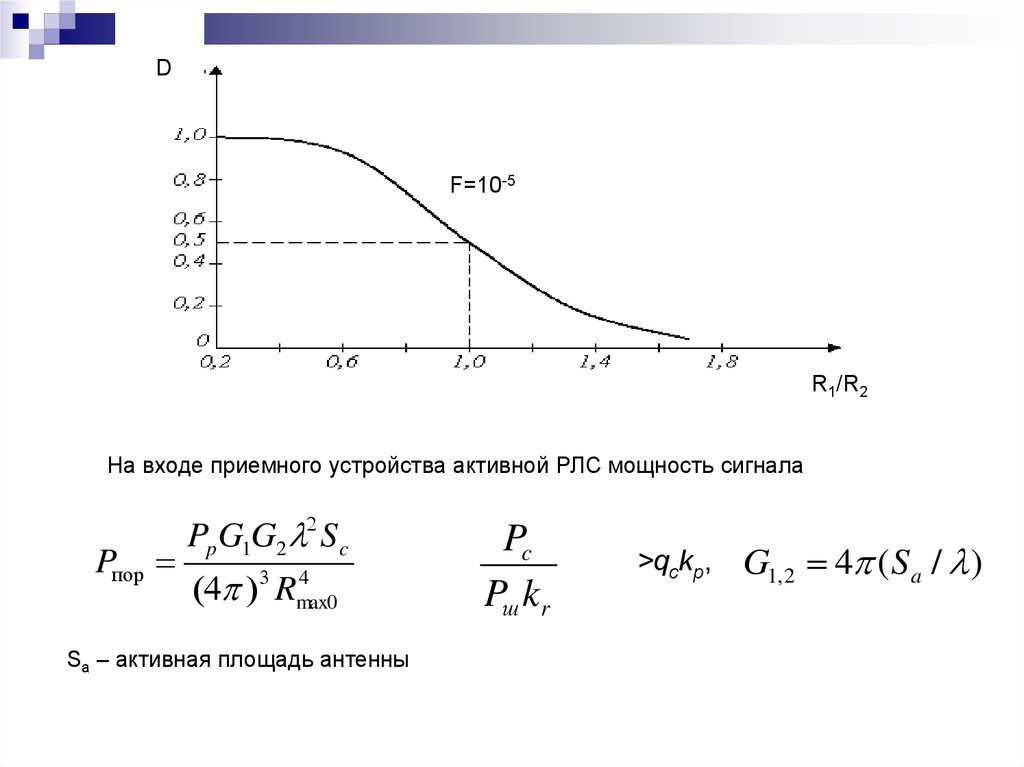
времени случайным образом. График иллюстрирует характер зависимости
относительного изменения дальности обнаружения от значения вероятности
правильного обнаружения D при заданной ложной тревоге F.
Вначале рассмотрим дальность действия РЛС без учёта влияния земной
поверхности и атмосферы на распространение радиоволн, т.е. РЛС и цель находятся в
«свободном» пространстве.
23.
3В условиях нестационарной
помеховой обстановки зону
обзора РТС (в частности, РЛС)
удобно представить в виде
ячеистой модели: n0 = nRn n .
ДНА РЛС
ПАП
Сигнал, помеха и шум в пределах
колец дальности имеют гауссовское
распределение вероятности. Вводится
временной
интервал
квазистационарности
помеховой
обстановки: Tз < Tкв < Tобз.
Цель 2
Анализируемый
элемент
разрешения по
дальности
Цель1
F=1/Tобз
РЛС
Пассивные
отражатели
Тип РЛС: когерентно-импульсная.
Отраженный
сигнал
–
квазидетерминированный
с
нефлуктуирующей амплитудой: s(t) = A(t – )cos[2 (f0 + Fд)(t – ) + 0].
24.
DF=10-5
R1/R2
На входе приемного устройства активной РЛС мощность сигнала
Pпор
Pp G1G2 S c
R
4
max0
Sa – активная площадь антенны
Pc
Pш k r
>qckp,
G1, 2 4 ( S a / )
25.
Rmax04
Pp G1G2 S c
Pпор
Rmax0
4
Pp S a1S a 2 S c
2 Pпор
Для РЛС с активным ответом
Rmax0
Pp G1G2 S c
Pпор
Rmax0
Pp S a1S a 2 S c
2 Pпор
Дальность действия запросчика и ответчика должны быть эквивалентными.
При прямолинейном распространении радиоволн дальность действия, кроме того,
Ограничивается зоной прямой видимости:
Rпв 4,12( H h ) H H г H
H г h R sin
H R 2 /( 2 RЗ )
26.
Дальность действия РЛС в условиях пассивных помех пространствеPс=KSс,
Pп=KSп ,
где Sс, Sп – эффективные площади рассеяния цели и помехи,
K
Pp G 2
R
Pc
( Pп Pш ) k r
>qckp,
1 ln F
qc
1
ln D
ln F
1 kr k p
qс=
ln D
P0=
kс Pс / Pш
kп Pп / Pш 1
,
27.
где kс, kп – соответственно коэффициенты передачи по мощности сигнала и помехи.Pс P0
Pп Pш
μ=
kс=N;
kп=Pш/Pп, где N – число импульсов в пачке.
Pp =
(4 R Pш
S с kс
G
S п k п
Q
.
D F
qc
Соотношения позволяют отразить зависимость энергетических и
вероятностных
параметров
РЛС,
адекватно
отражающего
взаимозависимость параметров РЛС.
28.
Rmax01
2
Sп
1 – при действии пассивных помех;
2- при применении методов режекции
пассивных помех (РФ).
29.
30.
Классификация активных помехПо виду спектра
Заградительные
Прицельные
Ответные
По воздействию
Подавляющие
Маскирующие
Имитирующие
По виду сигнала
Импульсные
Непрерывные
АМ, ЧМ, АЧМ
АШМ, ЧШМ
Синхр. И несинхр.
Шумомодулирован.
Прямошумовые
Кратные ответные
31.
Дальность действия РЛС в условиях активных помехТипы активных помех: заградительные, прицельные (импульсные или непрерывные;
по частоте и направлению), маскирующие, уводящие, мерцательные, имитирующие,
ответные (однократные или многократные).
Рассмотрим заградительные и прицельные шумовые помехи.
Заградительные имеют ΔFп>> Δfпр.. Отношение Эп/ ΔFп – спектральная плотность
помех.
Энергетически выгоднее применение прицельных помех.
ΔFп≈ Δfпр. Отсюда следует, что параметр Эп/ ΔFп много меньше, чем для
заградительных помех и следовательно



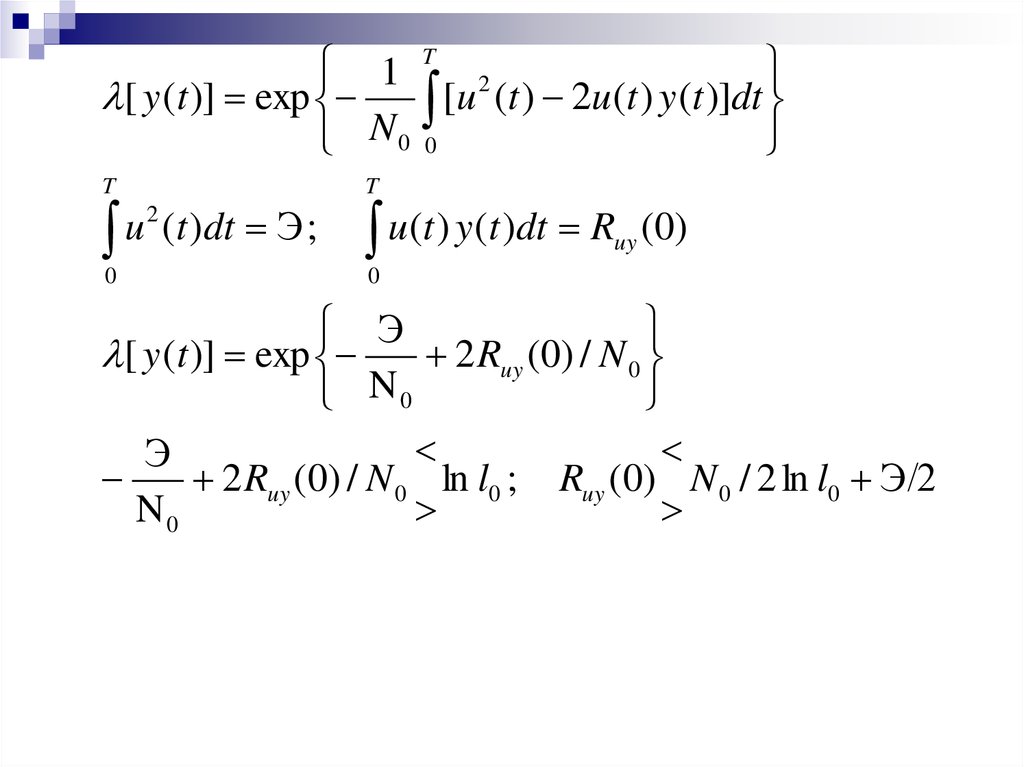
























 Физика
Физика








