Похожие презентации:
Теория симметричного вибратора
1.
Российский государственный университет имени И.КантаКафедра телекоммуникаций
Проектирование и расчет антенно-фидерных
устройств (АФУ)
Лекция №3
Теория симметричного вибратора
2. 1. Понятие симметричного вибратора
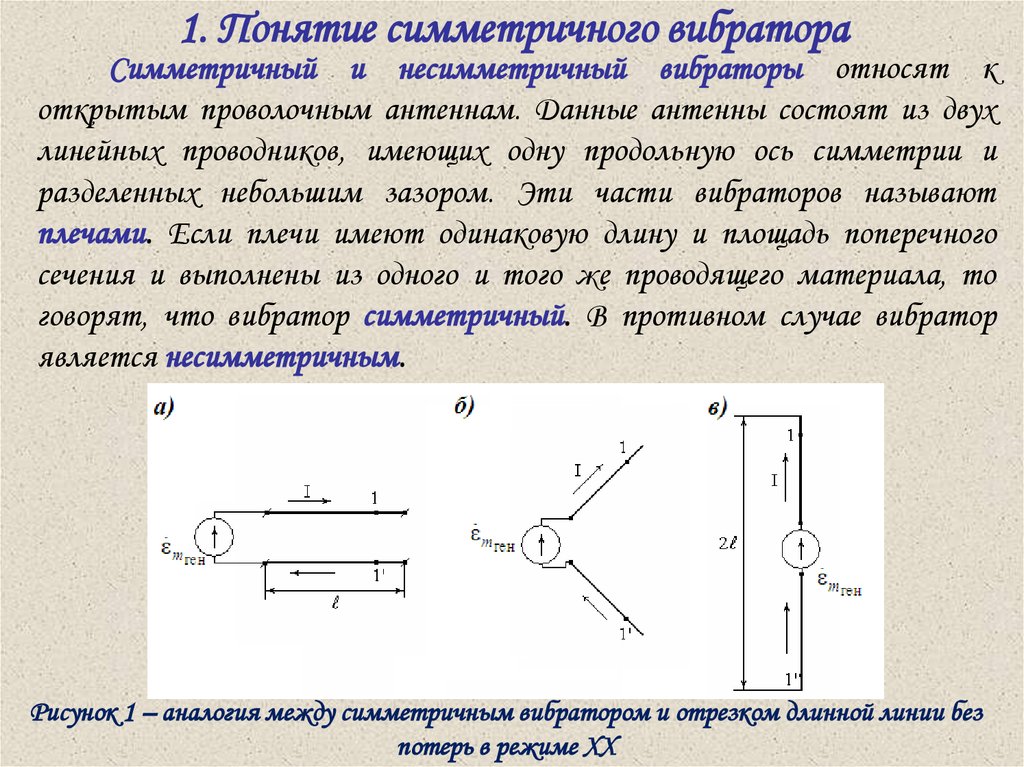
Симметричный и несимметричный вибраторы относят коткрытым проволочным антеннам. Данные антенны состоят из двух
линейных проводников, имеющих одну продольную ось симметрии и
разделенных небольшим зазором. Эти части вибраторов называют
плечами. Если плечи имеют одинаковую длину и площадь поперечного
сечения и выполнены из одного и того же проводящего материала, то
говорят, что вибратор симметричный. В противном случае вибратор
является несимметричным.
Рисунок 1 – аналогия между симметричным вибратором и отрезком длинной линии без
потерь в режиме ХХ
3. Конструктивное исполнение несимметричного вибратора
Рисунок 2 - Несимметричные вибраторыа) – несимметричный вибратор со смещенными клеммами;
б) – разноплечий вибратор;
в) – несимметричный вибратор над экраном конечных размеров
4.
Амплитудное распределение тока и напряжения вдольсимметричного вибратора
I m z I m sin k z
П
U m z U mП cos k z
где
k
2
- волновое число;
I mП и U mП - максимальные значения тока и напряжения в стоячей
волне, которые являются значениями амплитуд тока и напряжения в
пучности, координата z отсчитывается от середины симметричного вибратора.
Рисунок 3 – Амплитудные распределения тока и напряжения на симметричном вибраторе
малой длины
5.
Рисунок 4 – Амплитудные распределения тока вдоль симметричноговибратора произвольной длины
6.
Рисунок 5 – Амплитудные распределения заряда вдоль симметричноговибратора произвольной длины
7.
2. Поле излучения симметричного вибратораРисунок 6 - К определению поля излучения вибратора
8.
Поле от двух элементарных отрезков dz в точке М:e jr1k e jr2k
dE j 30k I m ( z )dz sin
e
r2
r1
Расстояния от первого и второго отрезков до точки М:
r1 r z cos
и
r2 r z cos
30kI m ( z )
dz e jkr sin e jkz cos e jkz cos e
r
60 I m z ke jkr
j
sin dz cos kz cos e
r
dE j
Просуммируем все поля в точке М, в результате получим:
j 60k e jkr
E dE e
sin I m ( z )cos kz cos dz
r
0
0
9.
Амплитуда напряженности электрического поля симметричного вибратора60 I mA cos( k cos ) cos k
Em
r sin k
sin
Нормированная амплитудная характеристика направленности
симметричного вибратора произвольной длины
Em
cos( k cos ) cos k
5
F( )
при 2
Emmax
( 1 cos k )sin
4
амплитудные характеристики направленности короткого симметричного
вибратора
f
k
2
2
sin
и
F sin
Нормированная ДН полуволнового вибратора:
cos cos
2
F
sin
10.
Рисунок 7 – Нормированные ДН симметричного вибратора11.
Выводы:1. При длине вибратора, много меньшей половины длины волны, ДН в
плоскости, содержащей вибратор, имеет два лепестка с
направлениями максимального излучения, перпендикулярными
продольной оси симметрии вибратора и направлениями нулевого
излучения вдоль оси вибратора.
2. С приближением длины вибратора к половине длины волны ширина
ДН уменьшается.
3. При длине вибратора, большей половины длины волны, но меньшей
длины волны, в ДН появляются боковые лепестки.
4. С приближением длины вибратора к длине волны происходит рост
относительного уровня боковых лепестков и уменьшение величины
поля в направлениях главного излучения.
5. При длине вибратора, большей длины волны, ДН приобретает
многолепестковый характер.
12.
3. Действующая длина симметричного вибратораКомплексная амплитуда электрического поля для диполя Герца
определена выражением
30k dz I m jkr
Em j
e F ,
r
где dz – геометрическая длина диполя Герца.
По аналогии комплексная амплитуда электрического поля для
любой линейной проволочной антенны может быть определена
выражением
Em j
где
30k
д
r
Im
e jkr F ,
д - действующая длина линейной проволочной антенны.
13.
Амплитуда напряженности электрического поля, создаваемогодиполем Герца и любой линейной проволочной антенной задаются
выражениями
60k д I mП
60k dz I m и
Em
Emmax
max
r
r
2
где k
- волновое число, рад/м;
I m ; I mП - величина тока и амплитуда тока в пучности в диполе
Герца и линейной проволочной антенне соответственно;
dz
д
r
- длина диполя Герца;
-действующая длина линейной проволочной антенны;
-расстояние
наблюдения.
от
излучающей
антенны
до
точки
Таким образом, действующая длина линейной проволочной антенны
есть коэффициент пропорциональности между максимальным значением
амплитуды напряженности электрического поля, созданного данной
антенной и максимальным значением амплитуды тока в ней.
14.
Рисунок 8 – Геометрический способ определения действующей длиныДля симметричного вибратора действующая длина может быть
рассчитана как
дA
2 1 cos k
k
tg
k sin k
2
,
4
15.
дп2
1 cos k
k
2 2 k
sin
2
,
4
Действующая длина полуволнового вибратора может быть
рассчитана как
дA
0.64 2
Действующая длина короткого в сравнении с длиной волны
вибратора равна половине геометрической длины антенны
дA
4. Сопротивление излучения и входное сопротивление симметричного
вибратора
Для расчета сопротивления излучения существует два метода: метод
интегрирования вектора Пойнтинга и метод наводимых Э.Д.С. В обоих
случаях сопротивление излучения определяется по формуле
P
R 2
I
16.
Предполагается, что рассматриваемая антенна располагается всвободном пространстве, мысленно окружается сферой большого
радиуса, после чего определяется поток мощности электромагнитных
волн, проходящих через указанную сферу в свободное пространство. Так
как потери в среде отсутствуют, то этот поток мощности и
определяет собою мощность излучения:
P Re E H dS ПdS
S
S
2
где
E
EE
E2
П
120 120 120
– численное значение вектора Пойнтинга;
Е – действующее значение напряженности электрического поля;
S - площадь сферической поверхности ;
dS – элементарная площадка данной сферы.
17.
Мощность излучения антенны будет определяться выражениемEm 2
1
P
dS
120 S 2
где Em - амплитудное значение напряженности электрического поля.
Для тонкого симметричного вибратора амплитудное значение
напряженности электрического поля зависит от меридионального угла
и определено в виде
60 I mA cos( k cos ) cos k 60 I mП
E m ,
f ,
r sin k
sin
r
Подставляя последнее выражение в предыдущее, получаем:
P
15I mП 2
cos( k cos ) cos k
sin
0 0
2
2
sin d d
18.
Производя интегрирование, оцениваем мощность излучения тонкого симметричноговибратора, а после деления на квадрат амплитуды тока в пучности имеем следующее
выражение для сопротивления излучения в пучности
RΣп 30{ Si 4k
C ln k
2Si 2k sin 2k
Ci 4k 2Ci 2k cos 2k
2 C ln 2k Ci 2k
}
где С - постоянная Эйлера; Сi и Si - интегральные синус и косинус.
Рисунок 9 – График зависимости сопротивления излучения в пучности от
относительной длины плеча вибратора
19.
Входное сопротивление симметричного вибратора носит комплексныйхарактер и складывается из двух составляющих: активной и реактивной
RA
R П
2
R П
2
где 120 ln
2
a
sin k
2
и
волновое
1 вибратора;
sin 2k
XA
2 R 2 П
2
sin
k
2
сопротивление
симметричного
- длина одного плеча симметричного вибратора;
а - радиус проводника, из которого изготовлен вибратор.
20.
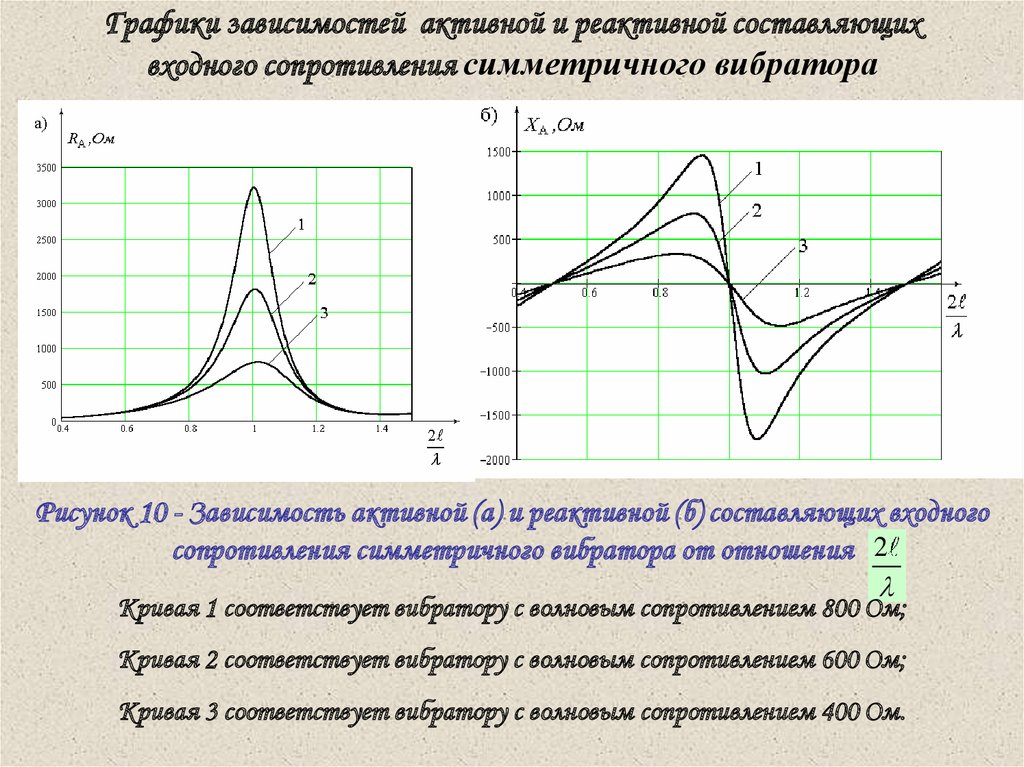
Графики зависимостей активной и реактивной составляющихвходного сопротивления симметричного вибратора
Рисунок 10 - Зависимость активной (а) и реактивной (б) составляющих входного
сопротивления симметричного вибратора от отношения 2
Кривая 1 соответствует вибратору с волновым сопротивлением 800 Ом;
Кривая 2 соответствует вибратору с волновым сопротивлением 600 Ом;
Кривая 3 соответствует вибратору с волновым сопротивлением 400 Ом.






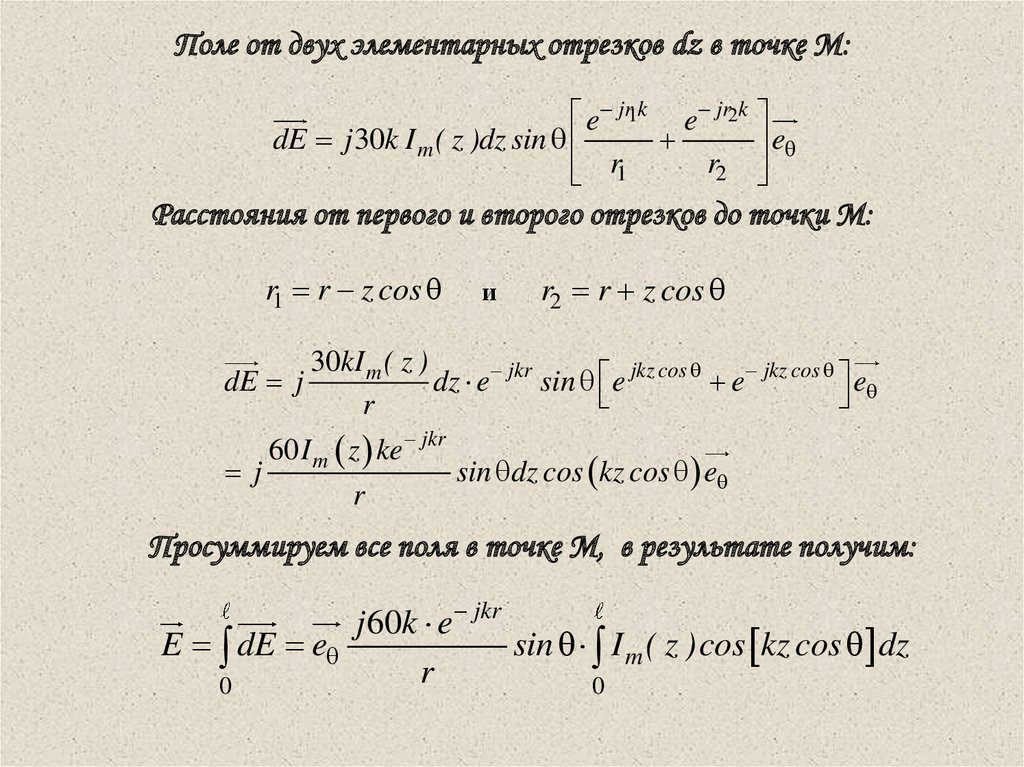












 Физика
Физика








