Похожие презентации:
Свободные колебания системы с бесконечным числом степеней свободы
1. Лекция 17-18 Свободные колебания системы с бесконечным числом степеней свободы
Содержание1.Свободные колебания балки с
распределенной массой.
2. Решение дифференциального
уравнения.
3. Ортогональность главных форм
колебаний
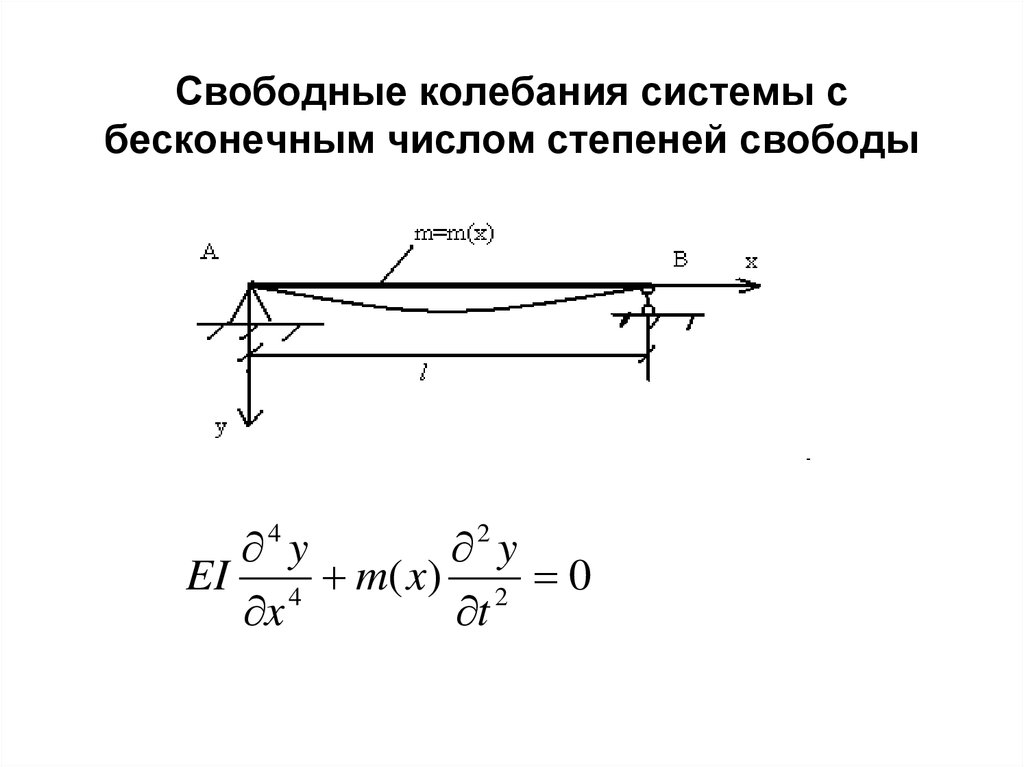
2. Свободные колебания системы с бесконечным числом степеней свободы
4 y2 y
EI 4 m( x) 2 0
x
t
3. Решение дифференциального уравнения свободных колебаний
y ( x, t ) y k ( x, t ) y k ( x)Tk (t ),k 1
k 1
k 1
k 1
EI ( y k( IV ) ( x)) m( x)( y k ( x)Tk// (t )) 0
4 y k ( x)
2Tk (t )
EI
Tk (t ) m( x) y k ( x)
0,
4
2
x
t
IV
k
//
k
EIy ( x)
T (t )
k2
m( x) y k ( x)
Tk (t )
k 1,2,3,.......
y kIV ( x ) s k4 y k ( x) 0,
k 1,2,3,....
m( x ) k2
s
EI
4
k
y ( x, t ) y k ( x)Tk (t ),
k 1
y k ( x) Ach( s k x) Bsh ( s k x) CCos( s k x) DSin ( s k x),
Tk (t ) Ak Sin k t Bk Cos k t ,
y ( x, t ) ( Ach( s k x) Bsh ( s k x) CCos( s k x) DSin ( s k x)) ( Ak Sin k t Bk Cos k t )
k 1
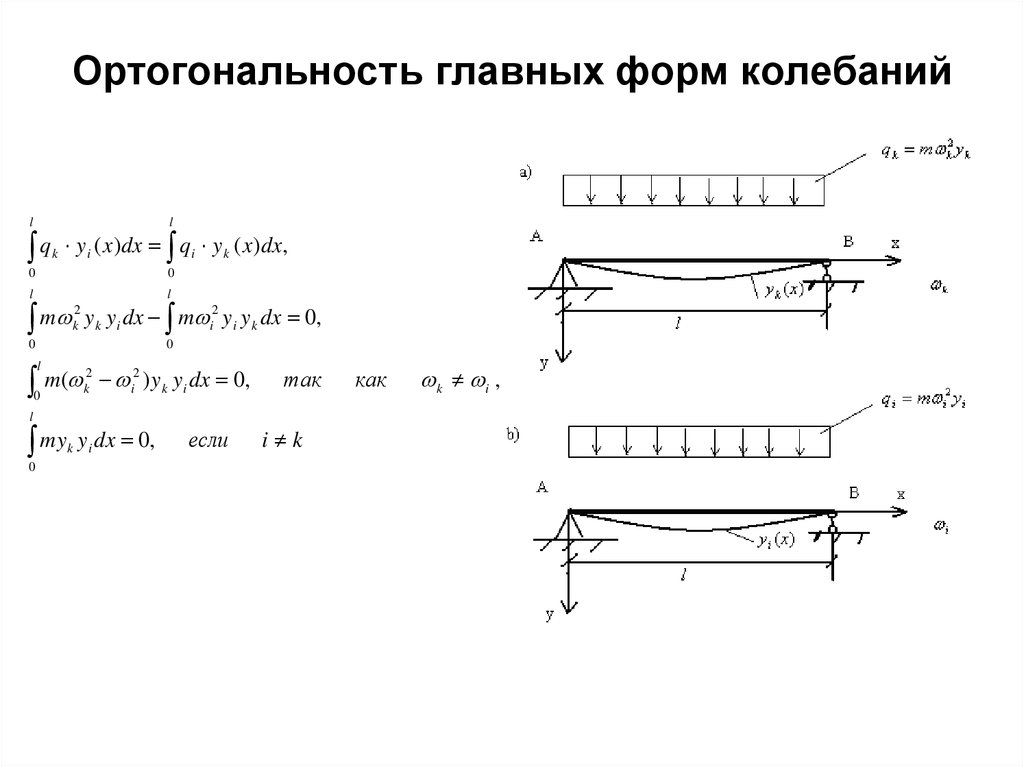
4. Ортогональность главных форм колебаний
lq
l
k
y i ( x)dx qi y k ( x)dx,
0
0
l
m
l
2
k
y k y i dx m i2 y i y k dx 0,
0
0
l
m(
0
2
k
i2 ) y k y i dx 0,
так
l
my
0
k
y i dx 0,
если
i k
как
k i ,
5. Метод начальных параметров
y k ( x) Ach( s k x) Bsh ( s k x) CCos( s k x) DSin ( s k x),y k/ ( x) s k Ash( s k x) s k Bch ( s k x) s k CSin ( s k x) s k DCos ( s k x),
y k// ( x) s 2 k Ach( s k x) s 2 k Bsh ( s k x) s 2 k CCos( s k x) s 2 k DSin ( s k x),
y k/// ( x) s 3 k Ash( s k x) s 3 k Bch ( s k x) s 3 k CSin ( s k x) s 3 k DCos ( s k x)
sk
4
m k2
EI
y k/ (0)
M (0)
Q (0)
y k ( x) y k (0) Ask x
Bsk x 2 k C sk x 3k Dsk x ,
sk
s k EI
s k EI
y k/ ( x) s k y k (0) Dsk x y k/ (0) Ask x
M k (0)
Q (0)
Bsk x 2k C sk x ,
s k EI
s k EI
M k ( x) y k// ( x) EI s 2 k y k (0) EIC sk x s k y k/ (0) EIDsk x M k (0) Ask x
Qk (0)
Bsk x ,
sk
Qk ( x) y k/// ( x) EI s 3 k y k (0) EIBsk x s 2 k y k/ (0) EIC sk x s k M k (0) Dsk x Qk (0) Ask x
6. Круговые функции
ch( sk x) Cos( sk x)Ask x
,
2
ch( sk x) Cos( sk x)
C sk x
,
2
sh( sk x) Sin ( sk x)
Bsk x
,
2
sh( sk x) Sin ( sk x)
Dsk x
2
k sk l ,
sk
4
m
EI
2
k
k s
2
k
EI
m
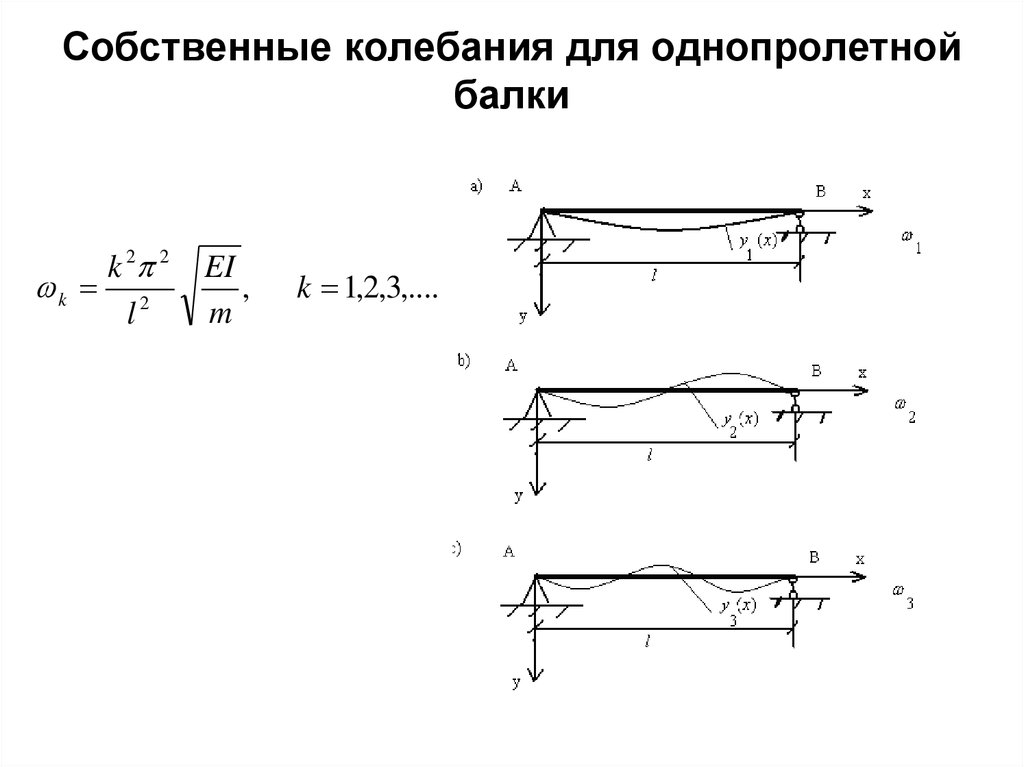
7. Собственные колебания для однопролетной балки
k 2 2k 2
l
EI
,
m
k 1,2,3,....
8. Частоты собственных колебаний для различных условий закреплений
Заделка с двухсторон
Один
конец
защемлен,
другой – свободен
Один конец защемлен,
другой – шарнирно оперт
4,7 2
1 2
l
EI
m
1,87 2
1 2
l
EI
m
3,9 2
1 2
l
EI
m
9. Приближенные методы определения частот собственных колебаний
Формула Дункерлея1
2
n
i 1
1
2
i
1
i
2
0
g
y ст
1
m 11
1
2
0
m( x) ii ( x)dx
Метод Рэлея
2 П м акс
2
n
l
M i X ( xi ) m( x) X ( x) dx
i 1
2
2
0
l
0






 Физика
Физика








