Похожие презентации:
Динамический расчет ферм
1. Лекция 15-16 Динамический расчет ферм
1.2.
3.
4.
Содержание
Свободные колебания ферм
Вынужденные колебания ферм
при вибрационной нагрузке
Динамический коэффициент
Пример динамического расчета
фермы
2. Динамическая степень свободы
n=2У-С0,где У – количество узлов, в которых
распределены массы фермы, С0 – количество
опорных связей, примыкающих к узлам с
сосредоточенными массами.
3. Расчетная схема фермы с конечным числом сосредоточенных масс
4. Уравнение для определения собственных частот
По аналогии с системами с n степенями свободы, записываемканонические уравнения через инерционные силы. Полагая
определитель системы равным нулю, получаем характеристическое
уравнение относительно неизвестного значения частоты свободных
колебаний ω (ω1, ω2 ,… ωn ). Обозначим параметр λ=1/ω2, тогда
вековое уравнение имеет вид:
(m1 11 )
m 21
m 2 12
...
m n 1n
(m 2 22 ) ...
mn 2n
...
...
m1 n1
m 2 n 2
...
...
... (m n nn )
0
5. Узловые перемещения
Вырежем из фермы любой узел k и рассмотрим его равновесие.Каждый соседний с ним узел обозначим индексом i, который при
записи канонических уравнений будет принимать конкретные
обозначения соседних узлов. Пусть перемещение узла k по
горизонтали будет x k , а по вертикали - y k.
Усилия в стержнях вырезанного узла фермы от статической нагрузки
или самоуравновешаны, если в узле нет нагрузки или находятся в
равновесии с узловой нагрузкой, если она есть.
Поэтому как заданные статические нагрузки, так и вызываемые ими
усилия стержней фермы из рассмотрения исключаются.
Будут рассматриваться лишь дополнительные усилия N ki,
появляющиеся в стержнях при колебаниях ферм, и инерционные
силы -
//
k
mk x ,
mk y
//
k
6. Уравнения динамического равновесия при свободных колебаниях
mk x N kt Cos kt//
k
mk y N kt Sin kt
//
k
7. Перемещения «k» и «i» узлов
8.
• Перемещение узла i обозначим - xi, yi, а новоеположение узлов точками - k/ l/ , а новая длина
стержня ki будет l/ki . Проектируя отрезок l/ki
на координатные оси, получаем:
lki/ Cos ki/ lki Cos ki xi xk ,
lki/ Sin ki/ lki Sin ki yi yk
lki/ lki lki
(lki/ ) 2 (lki Cos ki xi xk ) 2 (lki Sin ki yi y k ) 2
(lki/ ) 2 l 2 ki 2lki Cos ki ( xi xk ) Sin ki ( yi yk )
( xi xk ) 2 ( yi yk ) 2
(lki/ ) 2 2lki lki lki2 l 2 ki
2lki Cos ki ( xi xk ) Sin ki ( yi y k )
( xi xk ) 2 ( yi y k ) 2
9.
Пренебрегая в левой части величинойlki2
, а в правой части (xi-xk)2 и (yi-yk)2 как величинами малыми по
сравнению с остальными, тогда
l ki Cos ki ( x i x k ) Sin ki ( y i y k )
N ki
EА ki l ki
EA ki
Cos ki ( x i x k ) Sin ki ( yi y k )
l ki
l ki
m k x k//
m k y k//
Cos
) Sin
EA ki
Cos ki ( x i x k ) Sin ki ( y i y k ) Cos ki ,
l ki
EA ki
l ki
ki ( x i
x k ) Sin ki ( y i y k
x k a k Sin ( i t i ), y k b k Sin ( i t i ),
x k// i2 x k ,
y k// i2 y k
ki
10. Вынужденные колебания ферм при вибрационной нагрузке
Каноническиеуравнения
вынужденных
колебаний ферм при вибрационной нагрузке
P=P0 Sinθt аналогично тем, которые были
записаны для рам. Подставляя амплитудные
значения
инерционных
сил,
можно
канонические уравнения представить в виде
системы линейных алгебраических уравнений
относительно
неизвестных
амплитудных
значений инерционных сил Z1 , Z2 ,… Z n .
11. Канонические уравнения
Z1 ( 111
m1
2
) Z 2 12 ... Z n 1n Po 1 p 0,
Z1 21 Z 2 ( 22
1
m2
2
) ... Z n 2 n Po 2 p 0,
.........................................................................,
Z1 n1 Z 2 n 2 ... Z n ( nn
1
mn
2
) Po np 0
12.
11*
11
…..
Z1
*
11
1
m1
2
;
22
*
22
1
m2
;
2
*
nn
nn
1
mn
Z 2 12 ... Z n 1n Po 1 p 0,
Z1 21 Z 2 * 22 ... Z n 2 n Po 2 p 0,
..........................................................,
Z1 n1 Z 2 n 2 ... Z n
Zkx mk xk ,
2
*
nn
Po np 0
Zky mk yk
2
2
.
13. Нагрузки, действующие на узел k
14. Уравнения динамического равновесия
NN
mk xk// mk 2 xk
mk y
//
k
mk yk
Cos
2
ki
Cos ki Pkx Sin t ,
ki
Sin ki Pky Sin t
( y y ) Sin
EA ki
2
Cos
(
x
x
)
Sin
(
y
y
)
Cos
m
l
ki i
k
ki i
k
ki
k x k Pkx Sin t 0,
ki
EA ki
l
ki
ki ( x i x k ) Sin ki i
k
2
m
ki
k y k PkySin t 0





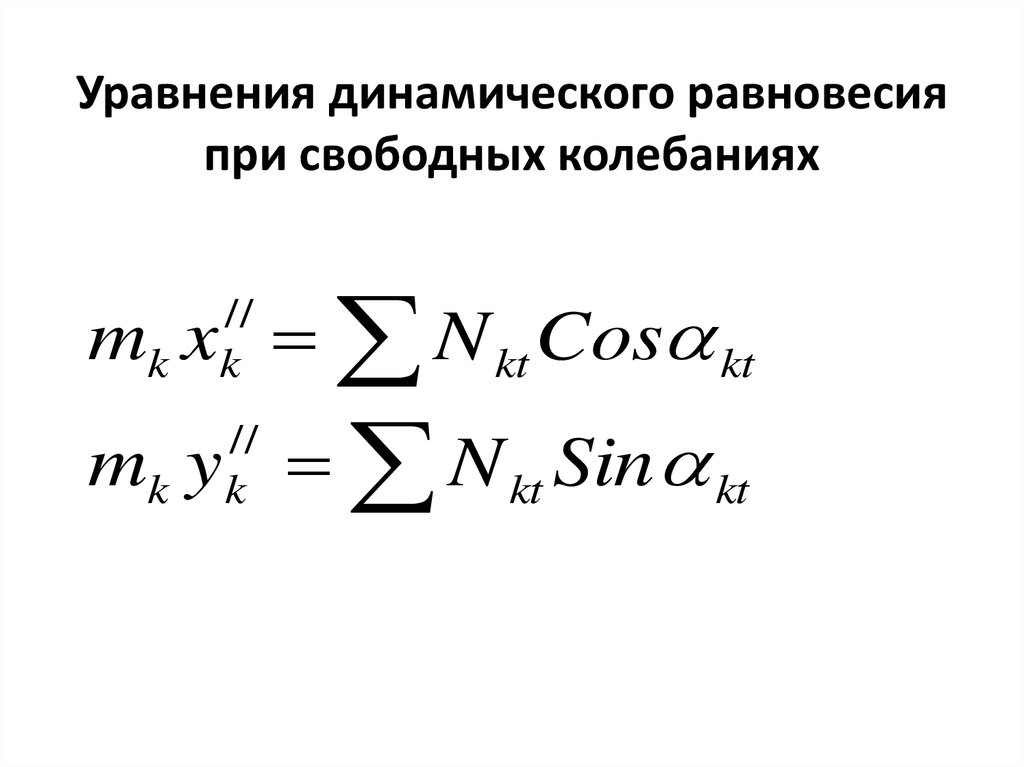








 Физика
Физика








