Скалярное произведение векторов

1.

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Скалярным произведением двух ненулевых
векторов называется произведение их длин на
косинус угла между ними.
a b = a b сos (a b )
Если хотя бы один из векторов равен нулю, то
скалярное произведение этих векторов равно нулю
(по определению).
Скалярное произведение векторов – число (скаляр).

2.

a b = 900
a b = a b cos 900
b
a
Если векторы a и b перпендикулярны, то
=0
скалярное произведение векторов равно нулю.
a b = 0 , то векторы a
Обратно: если
перпендикулярны.
и
b
Скалярное произведение ненулевых векторов равно
нулю тогда и только тогда, когда эти векторы
перпендикулярны.
a b = 0
a ^b

3.

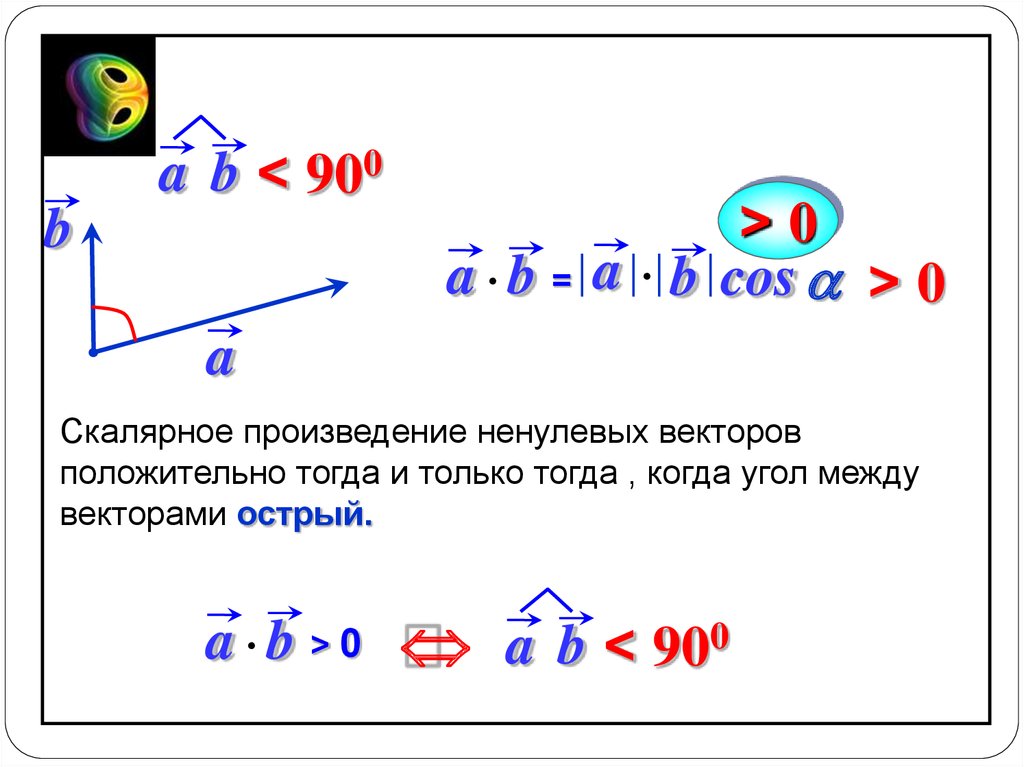
a b < 900
b
a b =
>0
a b cos a > 0
a
Скалярное произведение ненулевых векторов
положительно тогда и только тогда , когда угол между
векторами острый.
a b > 0 a b < 900

4.

a b > 900
a b = a b cos a < 0
b
a
Скалярное произведение ненулевых векторов
отрицательно тогда и только тогда , когда угол между
векторами тупой.
a b < 0 a b > 900

5.

Если
b
a
a
b
a b = 00
a b = a b cos 00 = a b
b
a
Если
a
b
a b = 1800
a b = a b cos1800 = – a b

6.

a a = 00
a
a a = a a cos 00 = a a
Скалярное произведение
a a
скалярным квадратом вектора
Таким образом,
a
2
=
a
2
=
a
2
называется
a
откуда
и обозначается
a2
2
a a .
Длина вектора равен квадратному корню из его
скалярного квадрата.

7.

Свойства скалярного произведения
1) a b a прa b b прb a.
cos
a
b ,
Действительно, прb a a
тогда
a b a b cos a b b прb a.
Отсюда следует формула для нахождения проекции одного вектора на другой:
a b
прb a
b
.
2) Переместительное или коммутативное свойство:
3) Сочетательное (ассоциативное) свойство:
a b b a.
a b a b a b .
4) Распределительное (дистрибутивное) свойство относительного
сложения векторов:
a b c a b a c.

8.

Скалярное произведение в координатной форме
a x bx a y by a z bz
Скалярное произведение двух векторов позволяет решить
некоторые задачи векторной алгебры:
1. Нахождение косинуса угла между двумя векторами.
a x bx a y by a z bz
cos a b
a x a y a z bx by bz
2
2
2
2
2
2
.
Отсюда следует условие ортогональности (перпендикулярности)
двух векторов в координатной форме:
axbx a yby azbz 0

9.

Пример 1. Даны вершины треугольника: A (2; –1; 3), B (1; 1; 1),
C (0; 0; 5). Найти ABC.
cos ABC
BA{1, 2, 2},
BA BC
.
BA BC
BA 1 4 4 3,
BC{ 1, 1, 4}, BC 1 1 16 3 2 ,
BA BC 1 2 8 9,
2
cos ABC
,
2
ABC 45о.

10.

2. Нахождение проекции одного вектора на направление другого.
Пример 2. Даны три точки A(2; 3; 5), B(1; 2; 2), C(3; 5; 4). Найти
пр ВС AB.
Решение
BC{2, 3, 2},
BC 4 9 4 17 ,
AB{ 1, 1, 3},
AB 1 1 9 11,
AВ BC 2 3 6 11,
AB BC
11
.
пр ВС AB
17
BC

11.

3. Нахождение длины вектора.
Пример 3. Дан вектор a m n, m n 2, m n .
3
Найти длину вектора
2
a a .
2
a.
Найдем скалярный квадрат вектора
2
a.
2
a ( m n) ( m n) m 2 m n n
2
1
m 2 m n cos m n n 4 2 2 2 cos 4 8 8 12.
3
2
2
2
a a 2 3.

12.

Определить длины диагоналей параллелограмма,
построенного на векторах a 2m n и b m 2n, где m, n –
единичные векторы, угол между которыми равен 60°.
2
2
2
d1 (3m n) (3m n) 9m 6m n n
2
9
6
1
1
cos
1 7.
9 m 6 m n cos m n n
3
2
2
2
d 2 (m 3n) (m 3n) m 6 m n cos m n 9 n 13.
2