Похожие презентации:
Динамика полета. Разгон и торможение самолета. (Лекция 7)
1. Динамика полета
Лекция 72.
Разгон и торможениесамолета
Под разгоном (торможением) самолета понимается
движение самолета в горизонтальном полете с
увеличением (уменьшением) скорости, т.е движение
с ускорением.
Силы действующие на самолет, будут теми же,
что и ГП. Уравнение движения:
dV
Тогда время разгона
V
dV m dt Pp X Pизб ;
от скоростиV1 до
t m
Pизб Ya G 0.
V
требуемой скоростиV2:
dV dV dL
dV
Выполним преобразования:
V
;
2
1
dt
Тогда длина участка
разгона (торможения):
dL dt
dL
V2
VdV
L m
Pизб
V1
3.
Определение областейразгона и торможения самолета
Pp X Pизб 0 разгон ВС
Pp X Pизб 0 торможение ВС
H=const
Pизб.
Pп
Pизб. max
Pр
0
Pизб>0
Vmax
-
Pизб<0
Vт.min
+
Pр
Vmax
V
V
Pнедост. max
P
4.
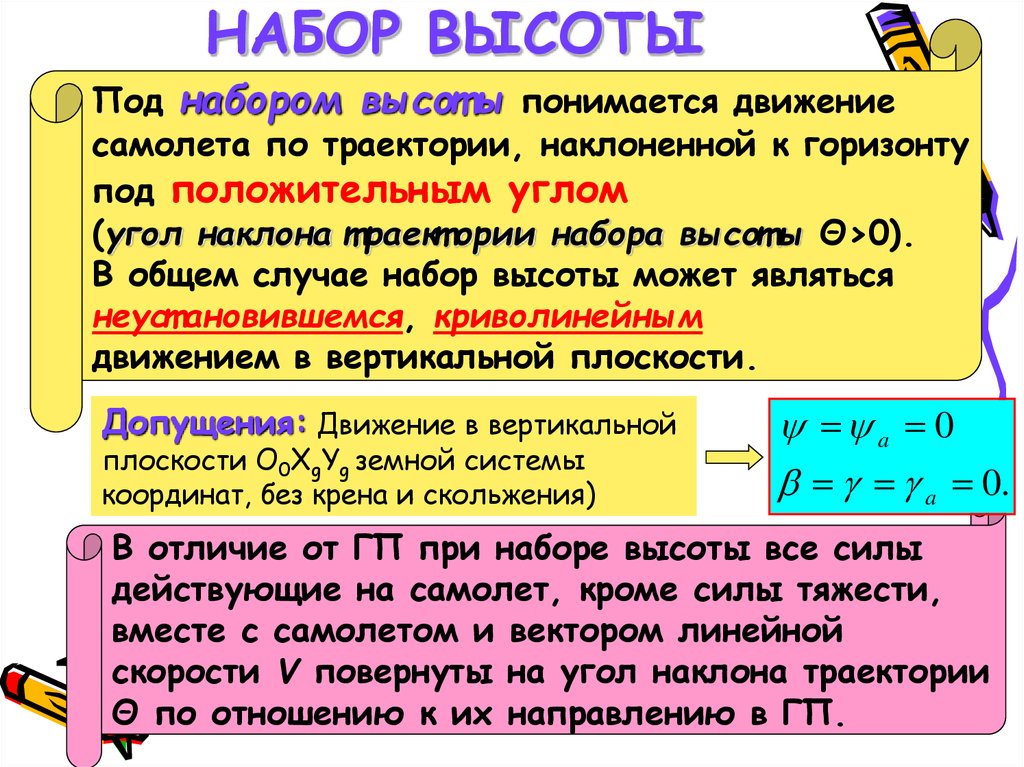
НАБОР ВЫСОТЫПод набором высот ы понимается движение
самолета по траектории, наклоненной к горизонту
под положительным углом
(угол наклона т раект ории набора высот ы Θ>0).
В общем случае набор высоты может являться
неуст ановившемся, криволинейным
движением в вертикальной плоскости.
Допущения: Движение в вертикальной
плоскости О0ХgYg земной системы
координат, без крена и скольжения)
a 0
a 0.
В отличие от ГП при наборе высоты все силы
действующие на самолет, кроме силы тяжести,
вместе с самолетом и вектором линейной
скорости V повернуты на угол наклона траектории
Θ по отношению к их направлению в ГП.
5.
Уравнения движения:Ya (Yк ) Yg
Ya
φдв P
αР
α
θ V
Горизонт
Xa
dV
m
Pp X G sin ;
dt
d
mV
Pp p Y G cos .
dt
0
p ДВ
Xg
Можно принять:
cos p 1, sin p p ;
Pp p Ya Ya .
G=mg
Тогда:
dV
dL
m
Pp X G sin ; x g
Vx V cos ;
dt
dt
d
dH
mV
Y G cos ;
y g
V y V sin .
dt
dt
6.
Условия набора высоты:dV
0
dt
неустановившегося
d
0
dt
криволинейного
При аэродинамическом расчете самолета
исследуется такой набор высоты, при котором
движение самолета мало отличается от
равномерного и прямолинейного
Тогда, при установившемся
прямолинейном наборе высоты:
Pp X G sin 0; Ya G cos 0;
Vx V cos ; V y V sin .
7.
Особенности набора высоты1. Если в ГП подъемная сила равна весу
(силе тяжести) самолета Ya G, то при наборе
высоты подъемная сила меньше веса в cosΘ раз,
так как Ya=GcosΘ.
2. Потребная скорость набора высоты VΘ при том
же суа меньше потребной скорости ГП в cos раз,
так как
2G cos
2G
V 2
V
Vг.п V 0
Ya c y
S G cos
Sc y
Scya
2
a
a
V Vг.п. cos
3. При наборе высоты с тем же углом
атаки, что и в ГП, сила лобового
сопротивления меньше в cosΘ раз, так как
8.
X a c xaV 2
S X a cx
a
2
2
Vг..п
2
S cos X a cos Pп cos
4. При наборе высоты требуется тяга не только
на преодоления лобового сопротивления, но и
составляющей силы тяжести, равной GsinΘ.
Тогда:
Pп Pп G sin , N п N п G sin V
Из принятых допущений получим:
Pр Pп Pизб G sin
откуда
Pизб
sin
G
9.
Потребные тяги и мощности самолетапри наборе высоты
Nпθ2
Nпθ1
N
Р
Р п θ2
Рп θ1
Nр
Gsinθ1V
Vmax θ
V2
Gsinθ2V
Рр
Gsinθ1
Gsinθ1
Рп
0
V1
ТРД
Nп
V
Vmax г.п.
0
V
Vmax θ Vmax г.п. V
ТВД
10.
Выводы:1. Набор высоты возможен только на тех скоростях, на которых
имеется (может быть создан) избыток тяги Ризб сверх лобового
сопротивления в ГП с той же скоростью.
2. Для получения кривой потребной тяги (мощности) при подъеме
с данным углом θ достаточно кривую потребных тяг для ГП
cдвинуть вверх (эквидистантно) на Gsinθ (а кривую потребной
мощности для ГП сдвинуть вверх на величину GsinθV.
3. Максимальная скорость по траектории, наклоненной к горизонту
под углом θ (Vmaxθ), будет меньше максимальной скорости вГП.
4. Для обеспечения подъема на заданной скорости под углом θ
необходимо увеличить тягу на Gsinθ или мощность двигателя на
GsinθV. При этом чем больше угол набора θ, тем больше должна
быть тяга.
5. Если весь имеющийся избыток тяги расходуется на набор высоты
(т.е. полет происходит без изменения скорости), то угол наклона
траектории при этом определяется из
Pизб
sin
G
11.
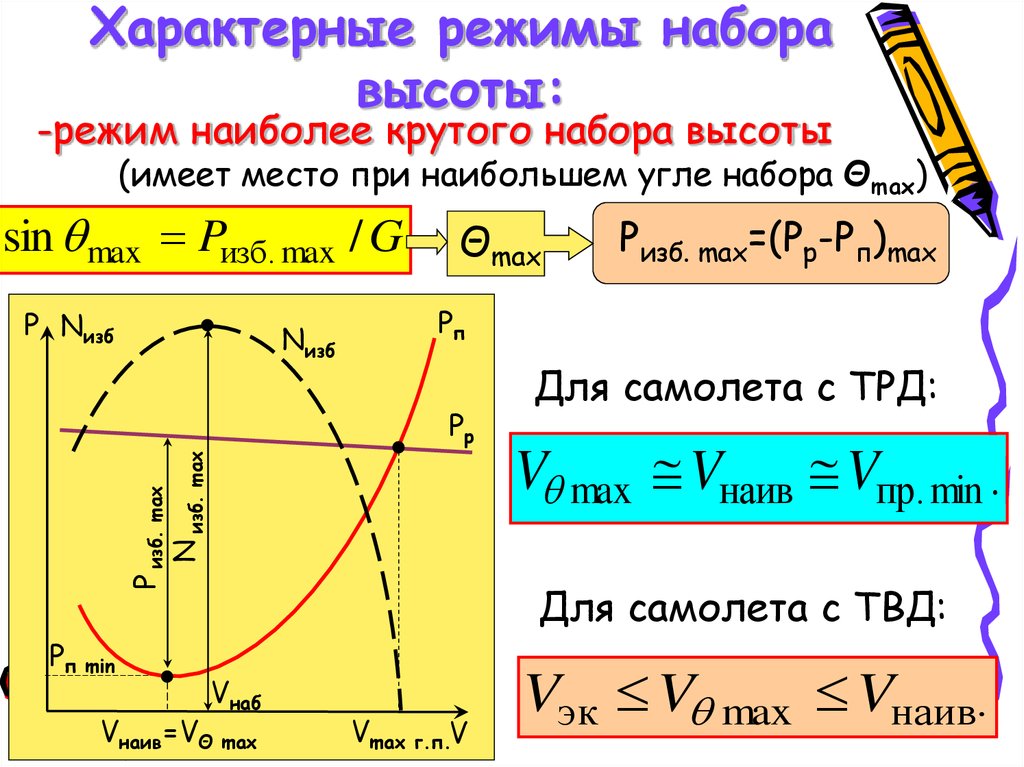
Характерные режимы наборавысоты:
-режим наиболее крутого набора высоты
(имеет место при наибольшем угле набора Θmax)
sin max Pизб. max / G
Р Nизб
Nизб
Θmax
Рп
P изб. max
N изб. max
Рр
Рп min
Pизб. max=(Pр-Рп)max
Для самолета с ТРД:
V max Vнаив Vпр. min
Для самолета с ТВД:
Vнаб
Vнаив=VΘ max
Vmax г.п.V
Vэк V max Vнаив
12.
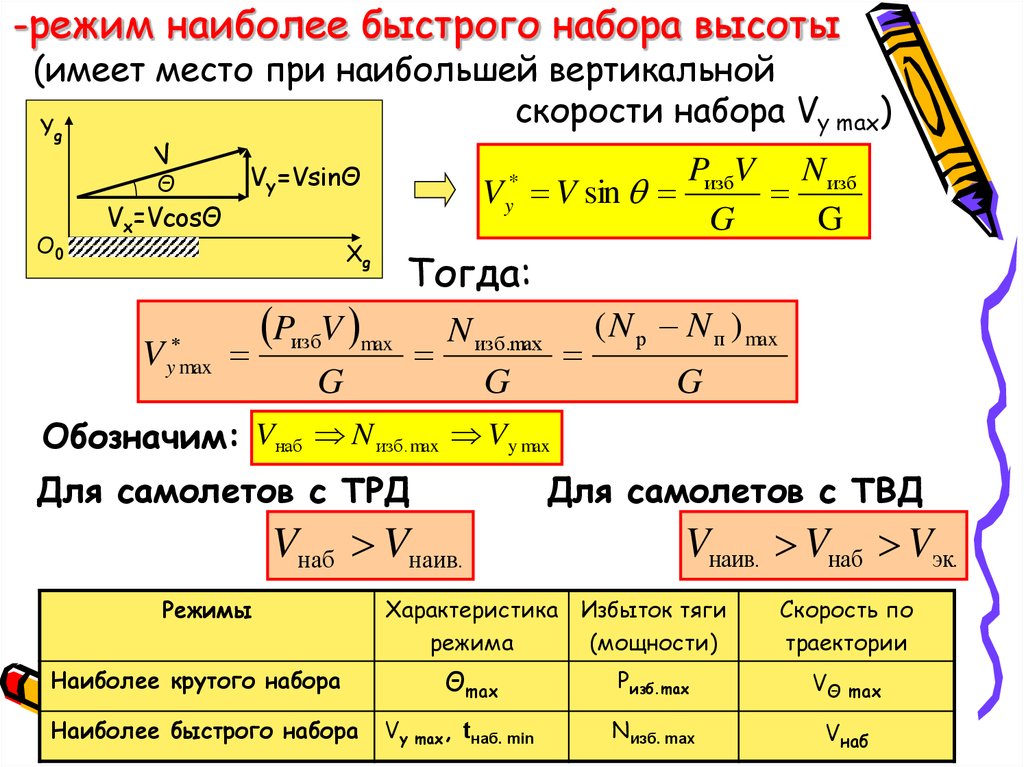
-режим наиболее быстрого набора высоты(имеет место при наибольшей вертикальной
скорости набора Vy max)
Y
g
Θ
O0
Vx=VcosΘ
V
y max
PизбV N изб
V V sin
G
G
Vy=VsinΘ
*
y
Xg
PизбV max
Тогда:
G
N изб.max ( N р N п ) max
G
G
Обозначим: Vнаб N изб. max Vy max
Для самолетов с ТРД
Для самолетов с ТВД
Vнаб Vнаив.
Режимы
Наиболее крутого набора
Наиболее быстрого набора
Vнаив. Vнаб Vэк.
Характеристика Избыток тяги
режима
(мощности)
Θmax
Vy max, tнаб. min
Pизб.max
Nизб. max
Скорость по
траектории
VΘ
max
Vнаб
13.
Влияние высоты полета на скоростьнабора высоты
Используя графики тяг (мощностей) Жуковского
для каждой принятой высоты рассчитаем:
Pр , Pп f (V ) Pр Pп f (V ) Pизб f (V )
PизбV f (V ) N изб f (V ) N изб max Vнаб V y max
Nизб
H
Hт
Nизб max
Н=0 км
11 км
3
6
Vmax
9
0
Vнаб
12
Vнаб.Н=0
Vнаб.Нт
НтV
V
14.
Влияние высоты полета намаксимальную вертикальную скорость
Н
H, км
НТ
Нпр
11 км
12
Высотный ТВД
10
Не
высотный
8
6
4
2
0
0,5 м/с
ТРД
VY*max
0
3
6
9
ТВД
12 VY*max,м/с
15.
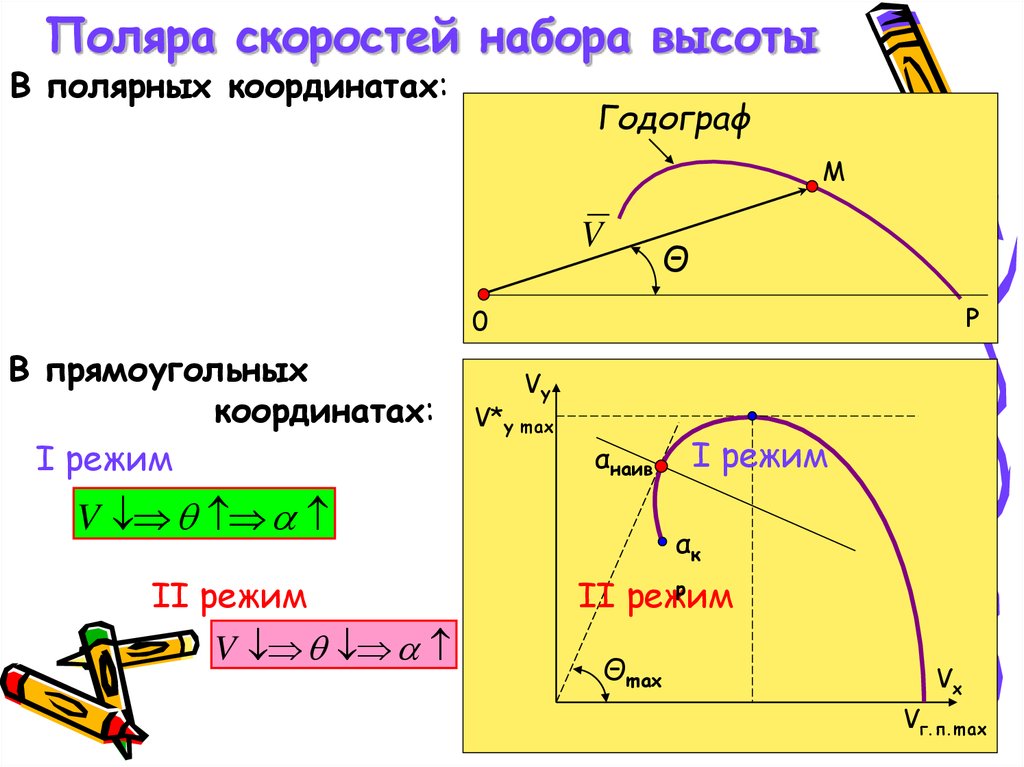
Поляра скоростей набора высотыВ полярных координатах:
Годограф
М
V
Θ
Р
0
В прямоугольных
координатах:
I режим
Vy
V*y max
αнаив
V
II режим
V
I режим
αк
р
II режим
Θmax
Vx
Vг.п.max
16.
Барограмма подъема самолета идальность набора высоты
Уравнения кинематических связей при НВ:
dH
dL
V y V sin
; V x V cos
.
dt
dt
На режиме наибольшей скороподъемности:
H
tнаб
dH
;
0 V y max
t
Lнаб Vнаб cos dt
0
Для перехода от переменной t к переменной Н :
V y dL Vнаб dH
dH V sin
tg tg sin
наб
V
Vx
dL V cos
V
y max
Vy
Тогда: L
наб
H
Vнаб / Vy max dH
O
17.
Алгоритм расчета дальности принаборе высоты
Исходными данными для расчета являются
зависимости
Vy*max f ( H ), Vнаб f ( H ).
1.Рассчитать и построить графики подынтегральных
функций
1 Vy*max f ( H ), Vнаб Vy*max f ( H ).
2.Разбить высоту Н на ряд элементарных участков ∆Н,
соблюдая условие, чтобы подынтегральная функция
на каждом принятом участке изменялась не более
чем в 1,5 раза.
3.Определить средние значения подынтегральной
функции на каждом из участков.
4. Найденные средние значения подынтегральной
функции умножить на принятый интервал
и этим определить время и дальность
набора за каждый интервал:
18.
tнаб 1 / V y maxLнаб
1 1
Н
ср
2 V y max
V
1
V
наб H наб
Vymax
V y max
2
ср
1
V y max
Hi
H
H i H
V
наб
Vymax
Hi
H i H
5. Последовательным суммированием найти время и
дальность набора
Н
Н
tнаб tнаб ,
Lнаб Lнаб .
высоты Н
Н 0
Н
Нпр
Н 0
Н
Нпр
Нр
Нр
0
tр
tН пр tнаб
0
Lнаб Нр
Lнаб Нпр L














 Математика
Математика Физика
Физика