Похожие презентации:
Динамика колебаний. (Раздел 2. Тема 8)
1. Раздел 2: Колебания и волны
Тема8. Динамика колебаний2. Тема 8. Динамика колебаний
1. Дифференциальное уравнение колебаний.Математический и физический маятники.
2. Свободные затухающие колебания.
3. Вынужденные колебания. Резонанс.
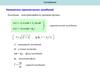
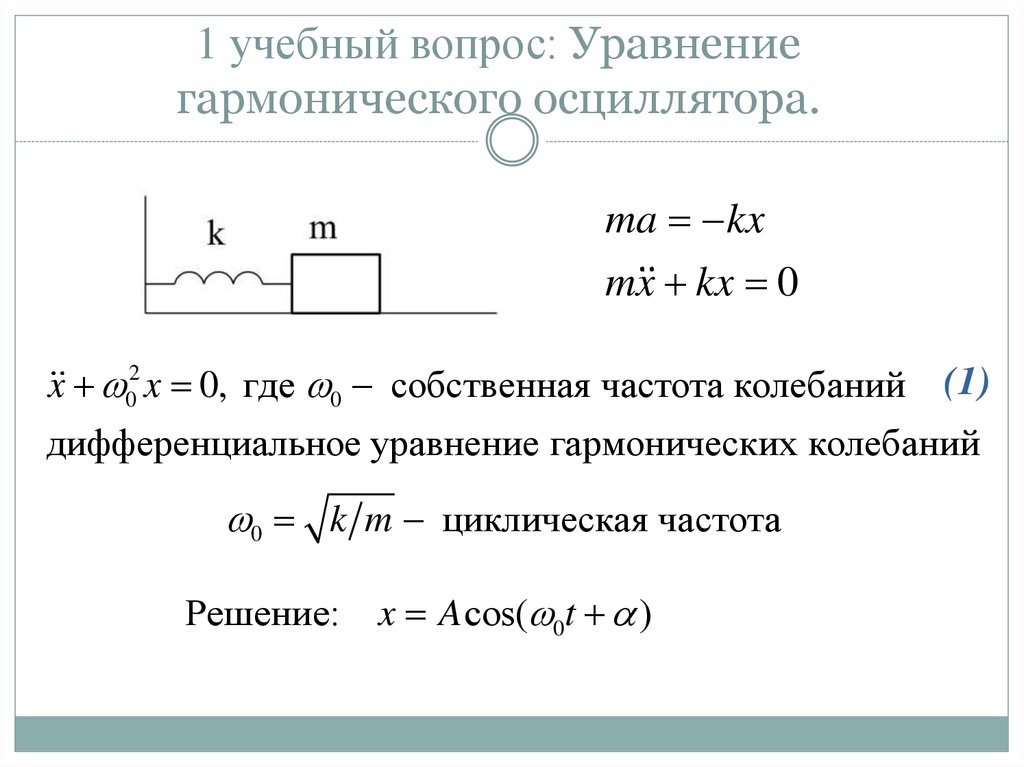
3. 1 учебный вопрос: Уравнение гармонического осциллятора.
ma kxmx kx 0
x 02 x 0, где 0 собственная частота колебаний
(1)
дифференциальное уравнение гармонических колебаний
0 k m циклическая частота
Решение:
x A cos( 0t )
4.
Математический маятникМатематическим маятником называют идеализированную
систему, состоящую из невесомой и нерастяжимой нити, на
которой подвешено тело с сосредоточенной в одной точке
массой, совершающее колебательное движение под
действием силы тяжести.
M J
J ml 2
ε d dt
2
2
M mgl sin
2
d
2
ml
mgl sin
2
dt
5.
2d
2
ml
mgl sin
2
dt
d 2 g
0 (2)
2
dt
l
sin
2
сравниваем с
d x
2
ω
0x 0
2
dt
2
l
g
T
2
(3)
0
0
g
l
Период колебаний математического маятника
зависит только от ускорения свободного падения и
от длины маятника и не зависит от его массы.
Решение:
A cos( 0t 0 )
(4)
6.
Физический маятникФизическим маятником называется любое твердое
тело, способное под действием силы тяжести
совершать колебания вокруг неподвижной оси, не
совпадающей с его центром инерции.
По аналогии с математическим маятником:
d 2
J
mgl sin
2
dt
В случае малых колебаний
d 2
2
ω
0 0
2
dt
mgl
ω
JO
2
0
(5)
7.
Решение дифференциального уравнения колебанийфизического маятника (5) имеет вид
JO
A cos( 0t 0 )
(6)
T 2π
mgl
J O J C ml
2
Сравним физический маятник с математическим
маятником
8.
Приведенной длиной физического маятниканазывается длина такого математического
маятника, период колебаний которого совпадает с
периодом колебаний данного физического маятника.
JO
T 2π
mgl
T 2
lпр
g
JO
lпр
(7)
ml
Точка О на прямой, соединяющей точку
подвеса с центром инерции, лежащая на
расстоянии приведенной длины от оси
вращения, называется центром качания
физического маятника.
9. 2 учебный вопрос: Свободные затухающие колебания
Fcопрdx
rv = r
dt
r коэффициент
сопротивления среды
Уравнение второго закона Ньютона:
d2 x
m 2 Fупр Fcопр
dt
d 2 x r dx k
x 0
2
dt
m dt m
2
r
m
ω02
k
m
d2 x
dx
m 2 kx r
dt
dt
d2 x
dx
2
2
0x 0
2
dt
dt
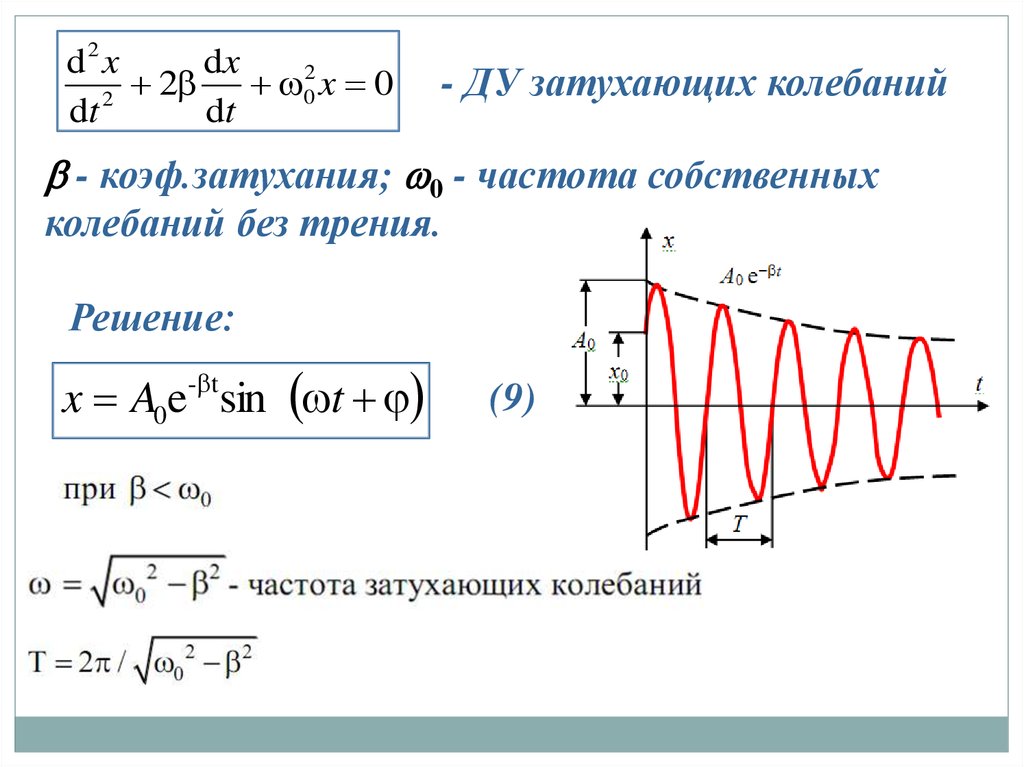
ДУ затухающих колебаний
(8)
10.
d2 xdx
2
2
0x 0
2
dt
dt
- ДУ затухающих колебаний
- коэф.затухания; 0 - частота собственных
колебаний без трения.
Решение:
x A0e- t sin t
(9)
11.
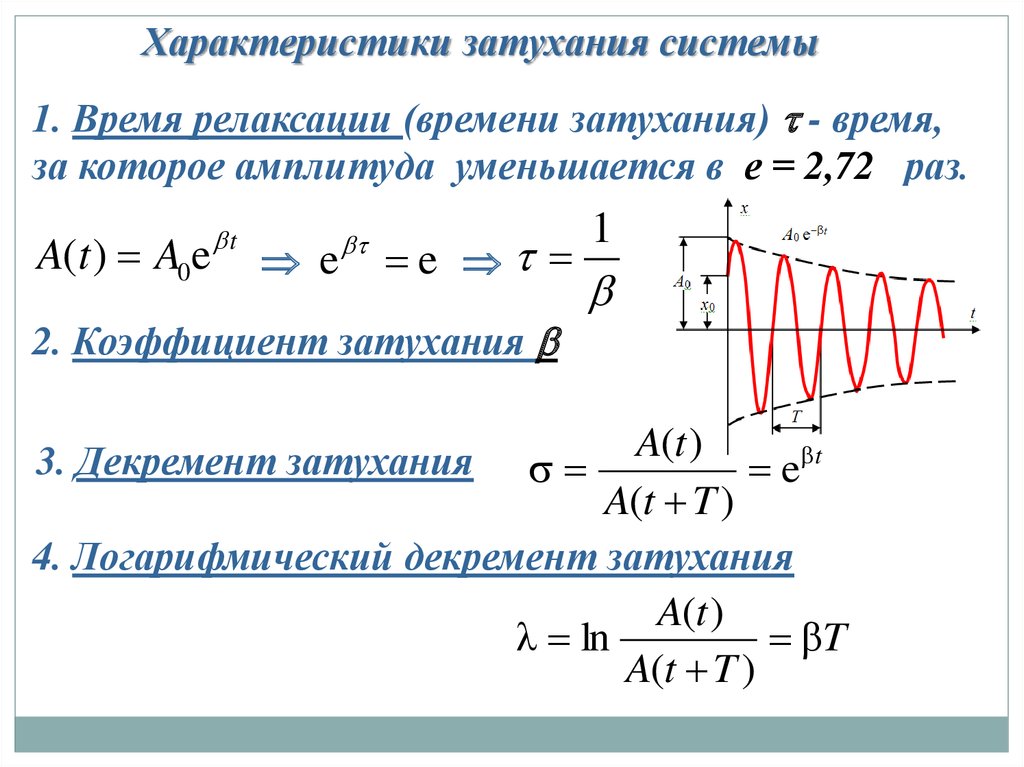
Характеристики затухания системы1. Время релаксации (времени затухания) - время,
за которое амплитуда уменьшается в е = 2,72 раз.
A(t ) A0e
t
e
e
2. Коэффициент затухания
1
A(t )
e t
A(t T )
4. Логарифмический декремент затухания
A(t )
λ ln
βT
A(t T )
3. Декремент затухания
12.
5. Добротность колебательной системы - числополных колебаний, совершаемых системой за время
затухания τ, умноженное на π:
Q
Q
T
Энергетический смысл добротности:
Добротность характеризует относительную убыль
энергии колебательной системы из-за наличия
трения на интервале времени, равном одному
периоду колебаний.
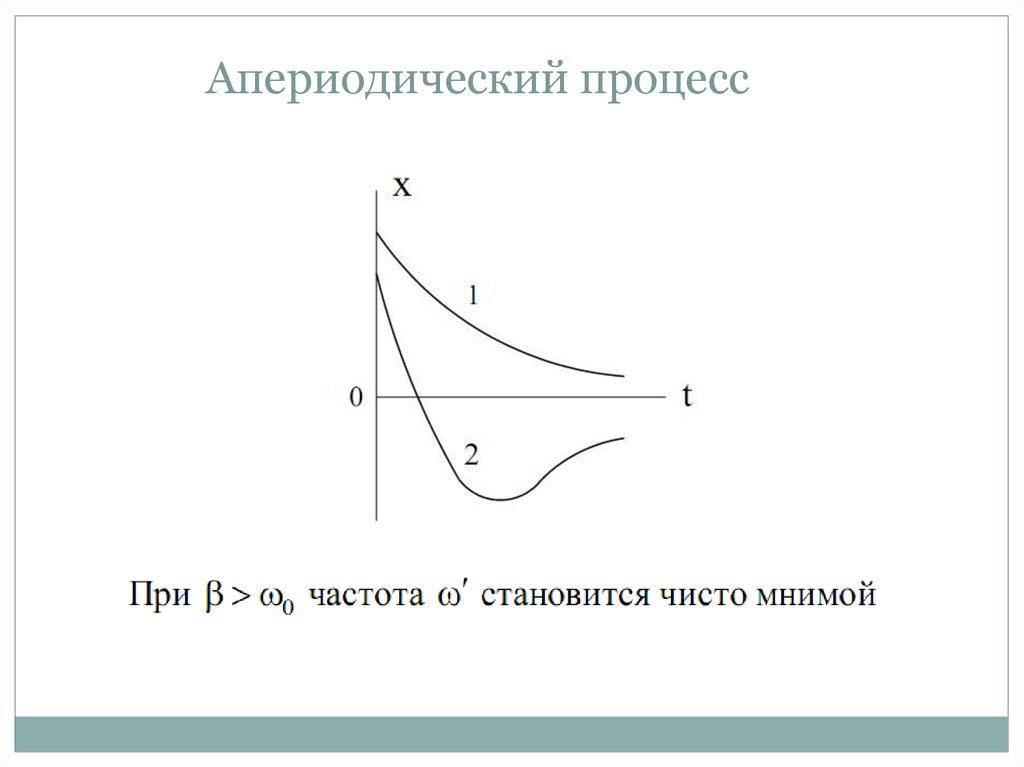
13. Апериодический процесс
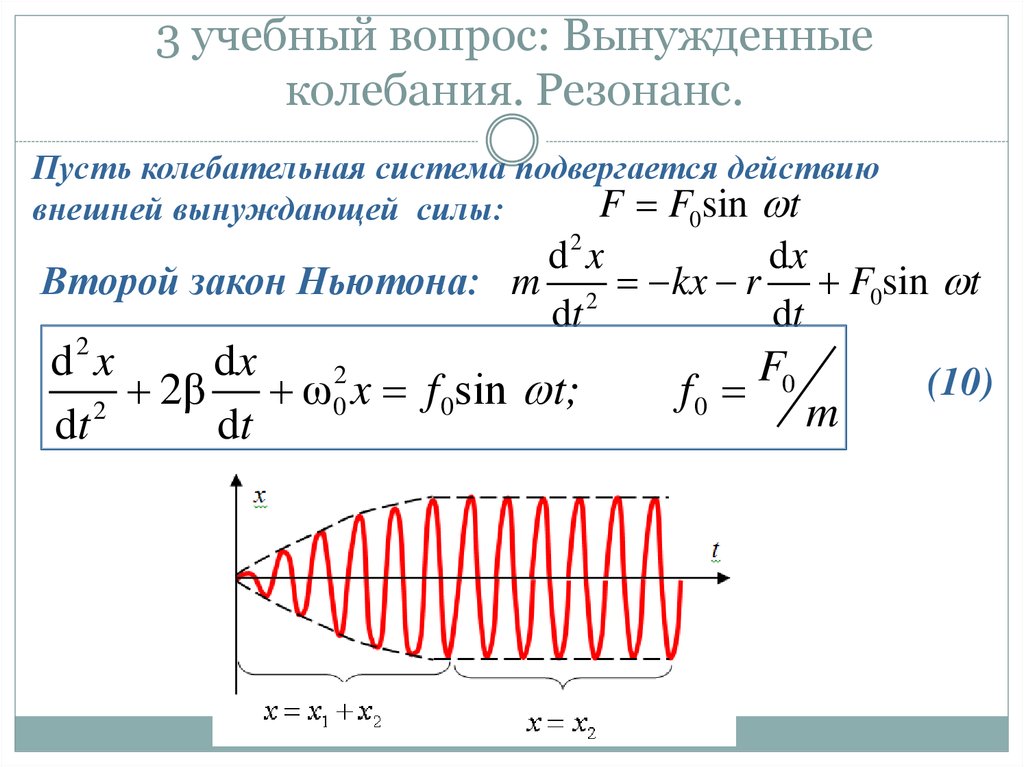
14. 3 учебный вопрос: Вынужденные колебания. Резонанс.
Пусть колебательная система подвергается действиюF F0sin t
внешней вынуждающей силы:
d2 x
dx
Второй закон Ньютона: m 2 kx r F0sin t
dt
dt
d2 x
dx
2
2β
ω
0 x f 0sin t;
2
dt
dt
f0
F0
m
(10)
15.
Решение: x2 A sinA
f0
4
2
2
2
0
2 2
t
(11)
2
tg 2
2
0
16.
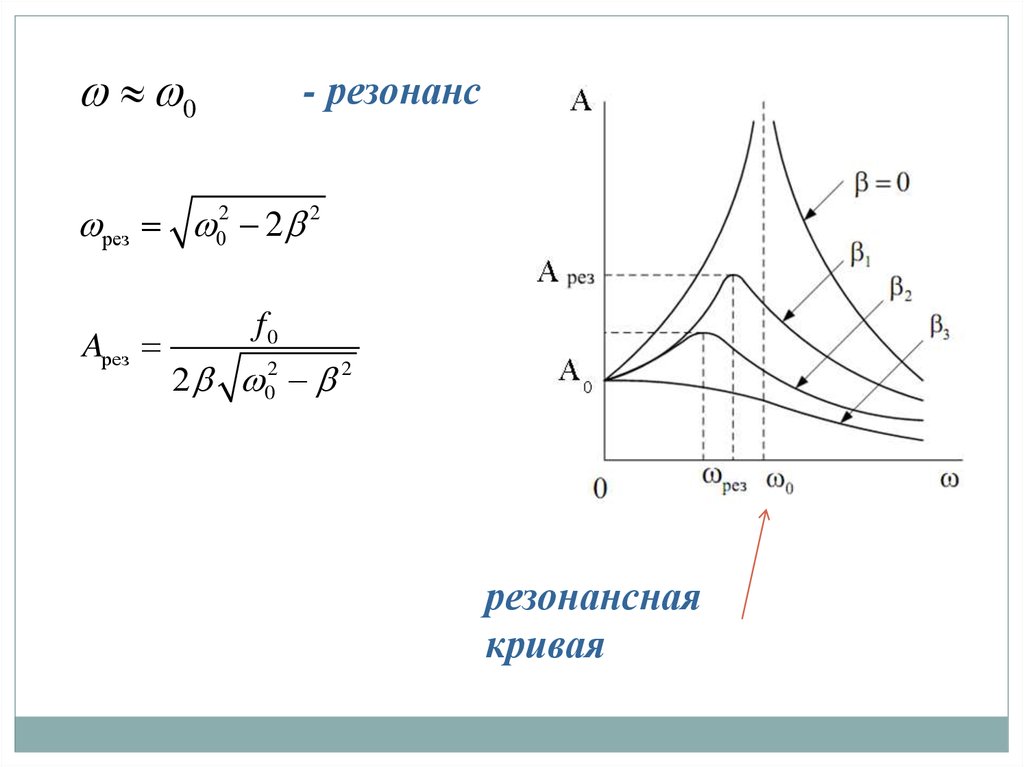
0- резонанс
рез 02 2 2
Aрез
f0
2 02 2
резонансная
кривая










 Физика
Физика