Задача 35

1.

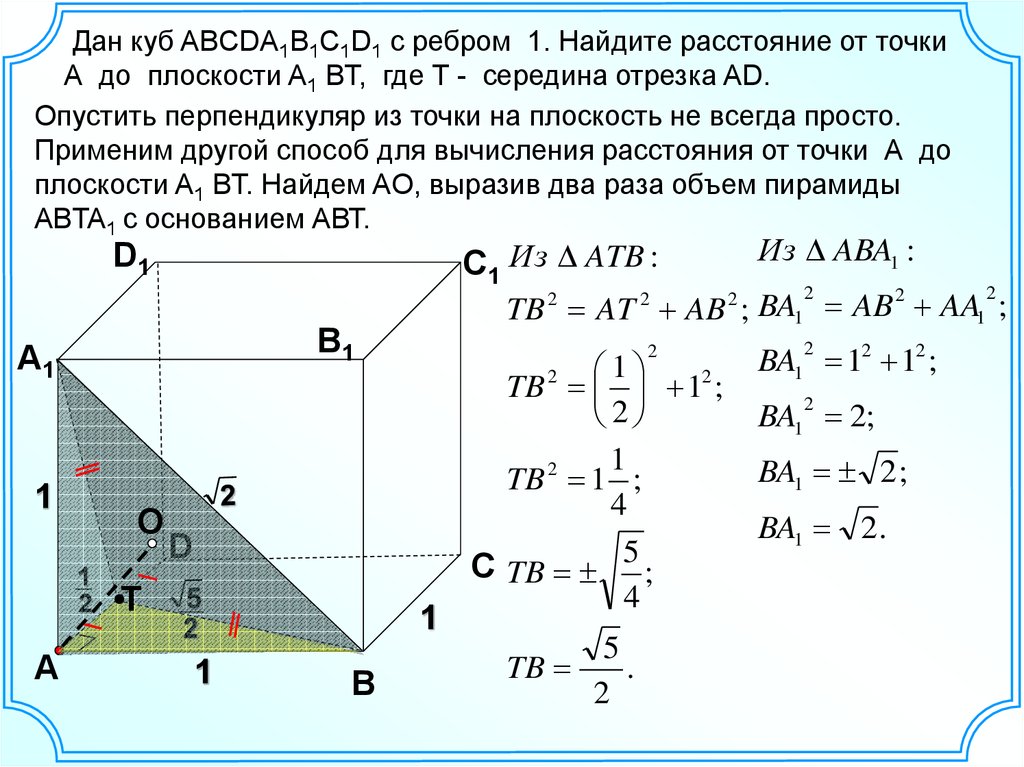
Дан куб ABCDA1B1C1D1 с ребром 1. Найдите расстояние от точки
А до плоскости A1 BТ, где Т - середина отрезка AD.
Опустить перпендикуляр из точки на плоскость не всегда просто.
Применим другой способ для вычисления расстояния от точки А до
плоскости A1 BТ. Найдем AO, выразив два раза объем пирамиды
ABTA1 с основанием АВТ.
2
TB AT AB ; BA1 AB AA1 ;
2
В1
А1
1
O
1
2
А
T
Из ABA1 :
С1 Из ATB :
D1
2
D
1
2
1
В
2
1
TB 2 12 ;
2
1
2
TB 1 ;
4
С TB 5 ;
4
5
TB
.
2
2
2
BA1 12 12 ;
2
BA1 2;
2
BA1 2 ;
BA1 2 .
2

2.

T
2
2
B
1
2
А
T
2
1
1
В
2
2
D
2
A1
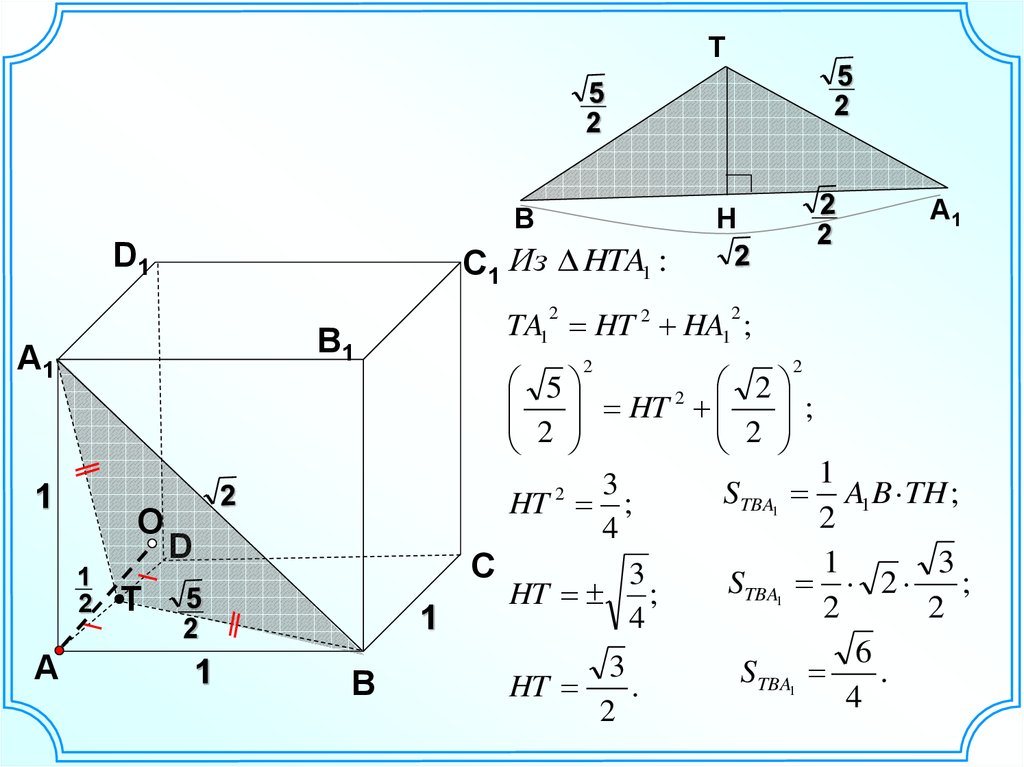
TA1 HT 2 HA1 ;
В1
А1
O
2
С1 Из HTA1 :
D1
1
H
2
5
2
HT 2
;
2
2
1
3
2
STBA1 A1 B TH ;
HT ;
2
4
1
3
С
3
STBA1 2
;
HT ;
2
2
4
6
3
S
.
TBA1
HT
.
4
2

3.

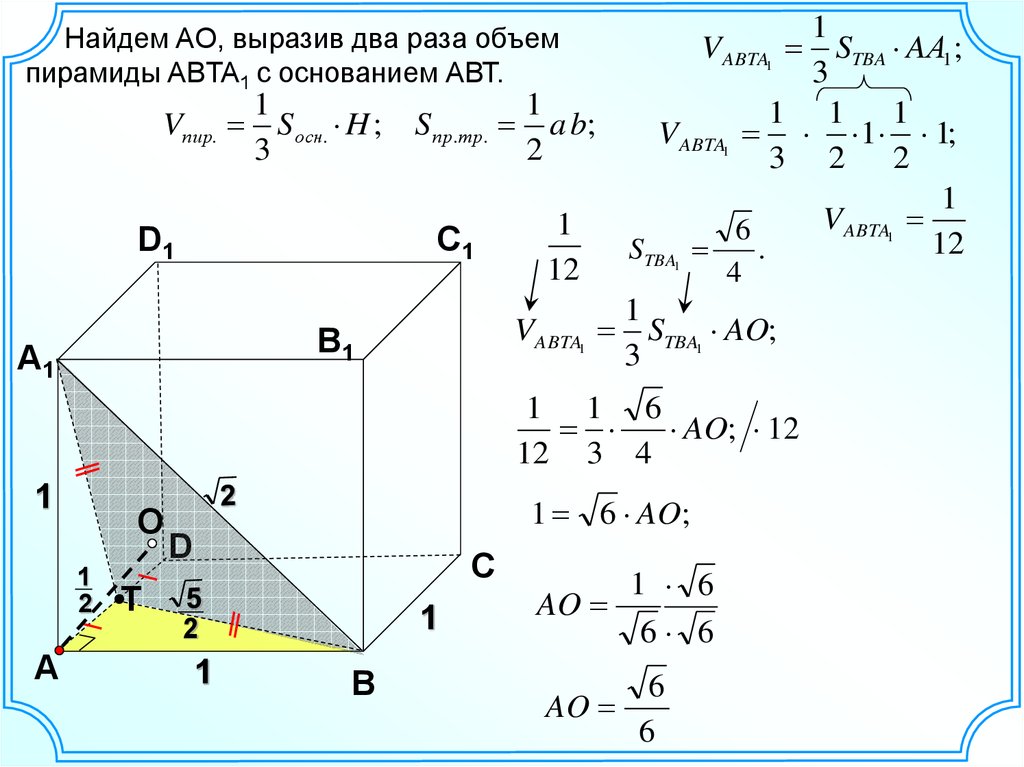
Найдем AO, выразив два раза объем
пирамиды ABTA1 с основанием АВТ.
Vпир.
1
S осн. H ;
3
S пр. тр.
С1
D1
1
12
1
4
1
VABTA1 STBA1 AO;
3
В1
А1
1
a b;
2
1
VABTA1 STBA AА1 ;
3
1 1 1
VABTA1 1 1;
3 2 2
1
V ABTA1
6
12
STBA
.
1 1 6
AO; 12
12 3 4
1
O
1
2
А
T
1 6 AO;
D
С
1
2
1
В
1 6
AO
6 6
AO
6
6