Похожие презентации:
Формула Тейлора
1. Математика Часть 1
УГТУ-УПИ2006 г.
2.
Лекция 7Формула Тейлора
1. Теорема Тейлора.
2. Оценка остаточного члена.
3. Разложение по формуле Маклорена
некоторых функций.
4. Приложения формул Тейлора
и Маклорена.
3.
1.Теорема Тейлора .
Если f(x) имеет в некоторой окрестности точки а
производные до (n+1) порядка включительно,
то существует окрестность этой точки,
в которой f(x) можно представить в виде
4.
f ( x) f (a)f ' (a)
1!
( x a)
f ' ' (a)
2!
( x a) ...
2
f ( n ) (a )
( x a )n Rn 1 ( x ),
n!
где
( n 1)
fс ( )
Rn 1 ( x )
( x aс)n 1 , a
x( , )
( n 1)!
c a ( x a), (0,1)
5.
Таким образом, для всех x из окрестноститочки a функцию f(x) можно представить так
f ( x ) Pn ( x ) Rn 1 ( x )
где
Pn ( x ) многочлен Тейлора,
Rn 1 ( x ) остаточный член.
6.
Частные случаи формулы Тейлора.. Формула Маклорена .
(Получается из формулы Тейлора при а = 0 )
f '(0)
f ''(0) 2
f ( x ) f (0)
x
x ...
1!
2!
f
где
( n)
(0) n
x Rn 1 ( x ),
n!
( x ) n 1
Rn 1 ( x )
x , (0,1)
( n 1)!
f
( n 1)
7.
2. Пусть f ( x ) многочлен степени n,то есть f ( x ) c0 c1 x c2 x ... cn x
2
Так как в этом случае
x
: f
n 1
( x)
0
f
Rn 1 ( x ) 0
n 1
(c )
0
f '(a )
f ''(a )
2
f ( x ) f (a )
( x a)
( x a ) ...
1!
2!
(n)
f (a )
n
( x a) ;
n!
n
8.
2. Оценка остаточного члена.Пусть f(x) такова, что
n , x : f
Рассмотрим
Rn 1 ( x )
f
n
( x ) M
( n 1)
f
(c )
n 1
Rn 1 ( x )
( x a) ;
( n 1)!
( n 1)
(c )
( n 1)!
x a
n 1
n 1
M
x a
( n 1)!
9.
Так какx a
n 1
( n 1)!
0
при
n , x a
Остаточный член может быть сделан сколь
угодно малым, путём увеличения n.
Формулу Тейлора можно использовать для
приближённых вычислений с любой степенью
точности.
10.
3. Разложение по формуле Маклоренанекоторых элементарных функций.
1.
f ( x) e
x
f (0) 1
f '( x ) e ;
f '(0) 1;
f ''( x ) e x ;
f ''(0) 1;
x
f
( n)
( x) e ;
x
f
(n)
(0) 1;
Формула Маклорена примет вид
11.
2n
x
x
x
ex 1
...
Rn 1 ( x )
1! 2!
n!
x
e
n 1
Rn 1 ( x )
x
n 1 !
Рассмотрим ( r , r ) окрестность точки x = 0.
f
( n)
( x ) e , n, x ( r , r )
r
r
e
Rn 1 ( x )
r n 1
n 1 !
12.
2.f ( x ) sin x
f ( x ) sin
x n
; f (0) 0.
2
0,
n
÷¸
ò
í
î
å
.
( n)
f (0) sin
n n 1
2 , n í å÷¸ ò í î å.
2
1
(n)
3
5
x x
x
sin x
... Rn 1 ( x )
1! 3! 5!
(Нечётная функция sinx разлагается по
нечётным степеням x )
13.
3. f ( x ) cos xf ( x ) cos
x n
; f (0) 1.
2
0,
n
í
å÷¸
ò
í
î
å
.
(n)
f (0) cos
n n
2 , n ÷¸ ò í î å.
2
1
( n)
2
4
x
x
cos x 1
... R
( x)
n 1
2! 4!
(Чётная функция cos x разлагается по
чётным степеням x )
14.
4. f ( x ) ln(1 x )f
( n)
n 1
( 1) ( n 1)!
( x)
; f (0) 0.
n
(1 x )
f
(n)
(0) ( 1)
2
3
n 1
4
( n 1)!
n
x
x
x
n 1 x
ln(1 x ) x
... ( 1)
2
3
4
n
Rn 1 ( x )
15.
5.f
( n)
f ( x ) (1 xлюбое
) , число
.
n
( x ) ( 1)
( n 1)(1 x )
f
(n)
; f (0) 1.
(0) ( 1)
( n 1)
( 1) 2
(1 x ) 1 x
x ...
2!
( 1)
( n 1) n
x Rn 1 ( x )
n!
16.
Частный случайn
n( n 1) 2
n
(1 x ) 1 nx
x ... x
2!
n
-формула бинома Ньютона.
17.
4. Применение формул Тейлора и Маклорена.1. Приближённые вычисления:
f ( x ) Pn ( x , a ) Rn 1 ( x , a )
f ( x ) Pn ( x , a )
Rn 1 ( x , a )
абсолютная погрешность
приближённого равенства.
18. ууу
19.
Нужно уметь оценить абсолютную погрешность,т.е. решать неравенство
Rn 1 ( x , a )
степень точности приближенного равенства
Абсолютная погрешность не превосходит
20.
Пример.Вычислить значение e c точностью 10 .
3
Решение.
Рассмотрим функцию f ( x )
e .
x
Разложим её по формуле Маклорена :
2
n
x x
x
e 1
...
Rn 1 ( x )
1! 2!
n!
Положим x 1
1 1
1
e 1 ... Rn 1 (1),
1! 2!
n!
x
21.
eRn 1 (1)
,0 1
( n 1)!
e
Rn 1 (1)
, e 3
( n 1)!
3
Rn 1 (1)
( n 1)!
Далее ищем наименьшее n, удовлетворяющее
неравенству
3
( n 1)!
n 6
22.
Окончательно1 1
1 1957
e 1 ...
1! 2!
6! 720
Ответ:
1957
e
2, 718
720
23.
2. Приближение функции многочленом.f ( x ) Pn ( x , a )
n 1
f ( x ) f (a ) f '(a )( x a )
Частный случай
Справа - линейная функция
Такая замена называется
функции .
линеаризацией
24.
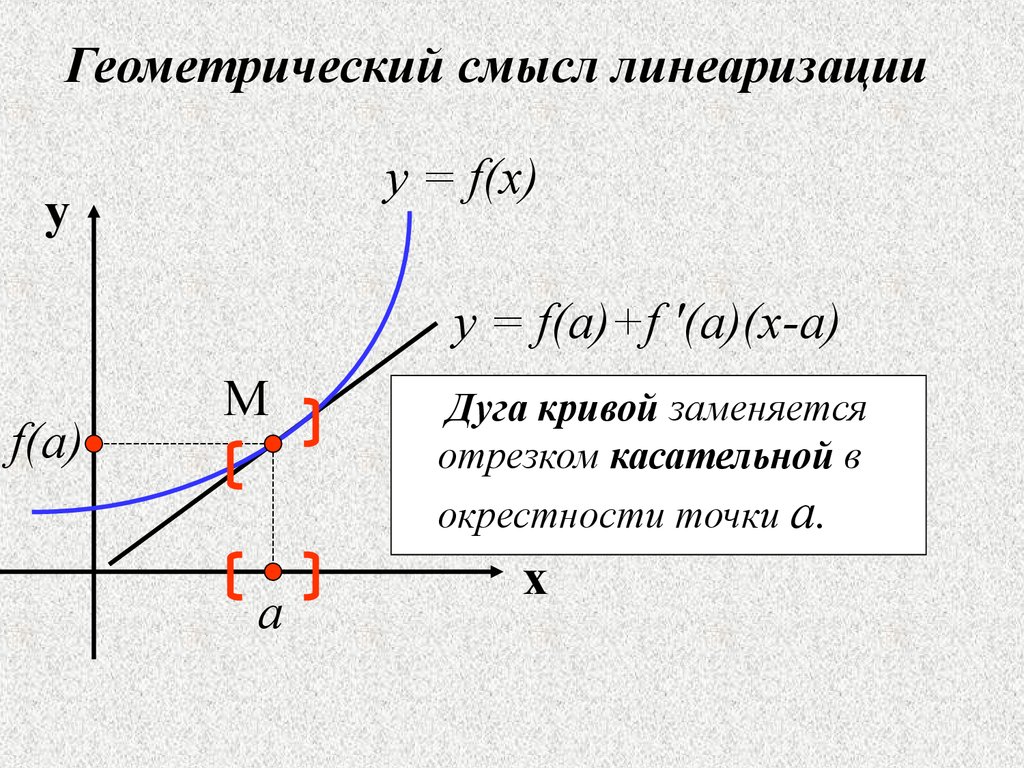
Геометрический смысл линеаризацииy = f(x)
y
y = f(a)+f '(a)(x-a)
f(a)
M
a
Дуга кривой заменяется
отрезком касательной в
окрестности точки а.
x
25.
3. Вычисление пределов.Пример.
Решение.
sin x x
?
lim
3
x
x 0
3
5
x
x
(x
...) x
sin x x
3!
5!
lim
lim
3
3
x
x
x 0
x 0
x3 x5
...
1
3!
5!
lim
.
3
3!
x
x 0














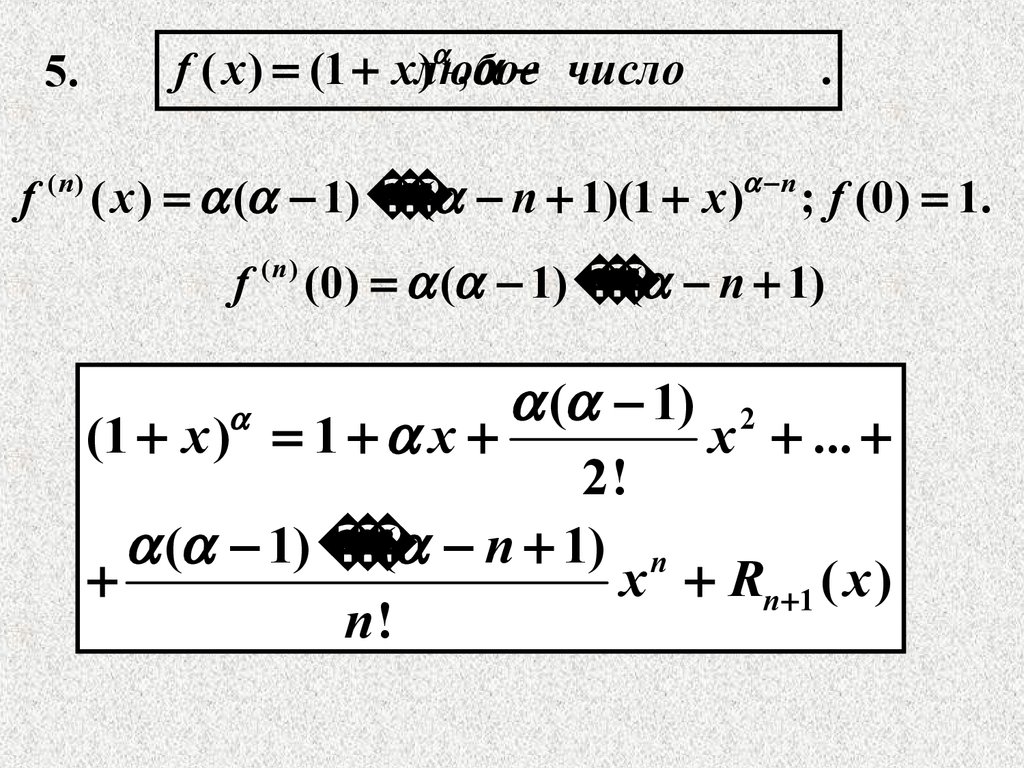









 Математика
Математика