Волны. Волновое уравнение

1.

Волны
Волна – процесс распространения колебаний в среде
Свойства волн:
1) переносят энергию и импульс;
2) не переносят вещество.
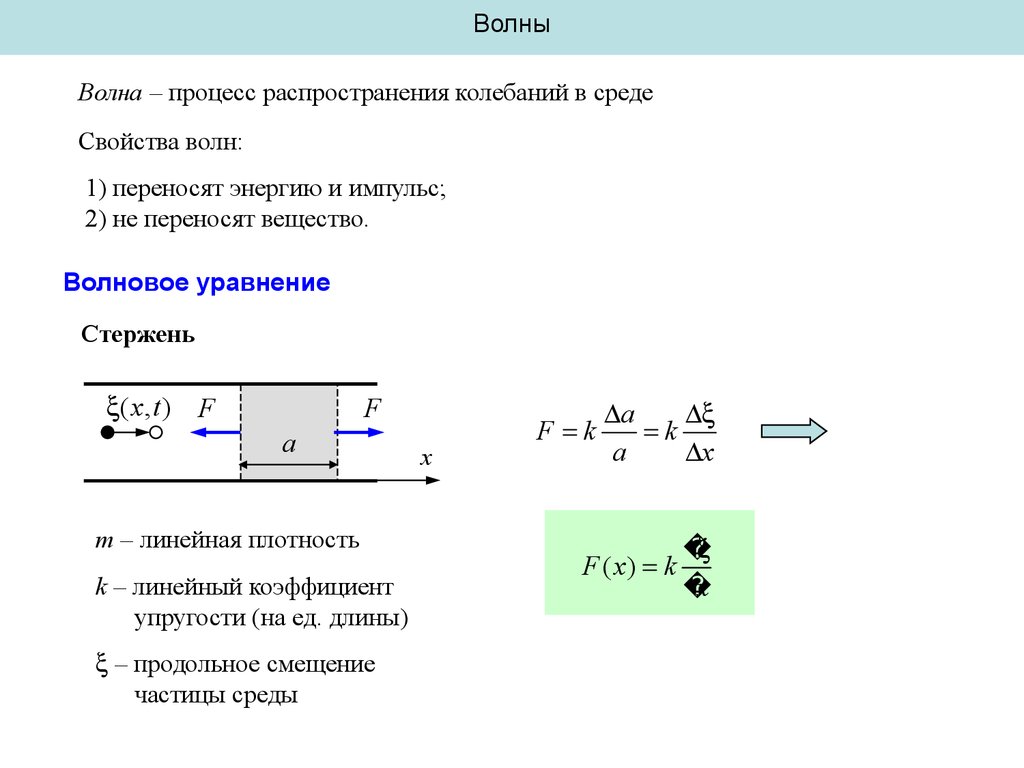
Волновое уравнение
Стержень
( x, t ) F
F
a
m – линейная плотность
k – линейный коэффициент
упругости (на ед. длины)
– продольное смещение
частицы среды
x
F k
a
k
a
x
F ( x) k
x

2.

Волны
Волновое уравнение
Уравнение движения
F ( x x )
F ( x)
2
m x 2
t
F ( x x ) F ( x )
x x 2
x
x
2
m x 2
t
x x 2
k
x
x x
: m x 0
x x
2 2 2
c
0
2
2
t
x
c
k
m
– скорость распространения упругих возмущений

3.

Волны
Волновое уравнение
Струна
y
y
T
T
Ty
( x, t )
T
x
x
m – линейная плотность
При << 1 T const
T – натяжение струны
– поперечное смещение
частицы струны
Ty T sin T tg T
<< 1
x

4.

Волны
Волновое уравнение
Уравнение движения
T ( x x )
y
2
m x 2
t
T ( x)
x
x
2
m x 2
t
T
x
x x 2
x x
Ty ( x x ) Ty ( x )
x x 2
: m x 0
x x
2 2 2
c
0
2
2
t
x
c
T
m
– скорость распространения малых возмущений

5.

Волны
Волновое уравнение
2 2 2
c
0
2
2
t
x
– классическое волновое уравнение
Решение – бегущие волны
c
1)
2)
( x, t ) ( t x c)
c
( x, t ) (t x c )
– “правая” бегущая волна
( x, t ) (t x c )
– “левая” бегущая волна
x
x
Продольная волна: (смещение частиц) ║ x (направление движения волны)
Поперечная волна: (смещение частиц) x (направление движения волны)

6.

Волны
Волновое уравнение
Гармоническая бегущая волна
A cos t x c
A cos( t kx )
k
c
– гармоническая бегущая или
плоская монохроматическая волна
– волновое число (вектор)
y
x
c
– частота волны
2
T
1
– длина волны
– период волны

7.

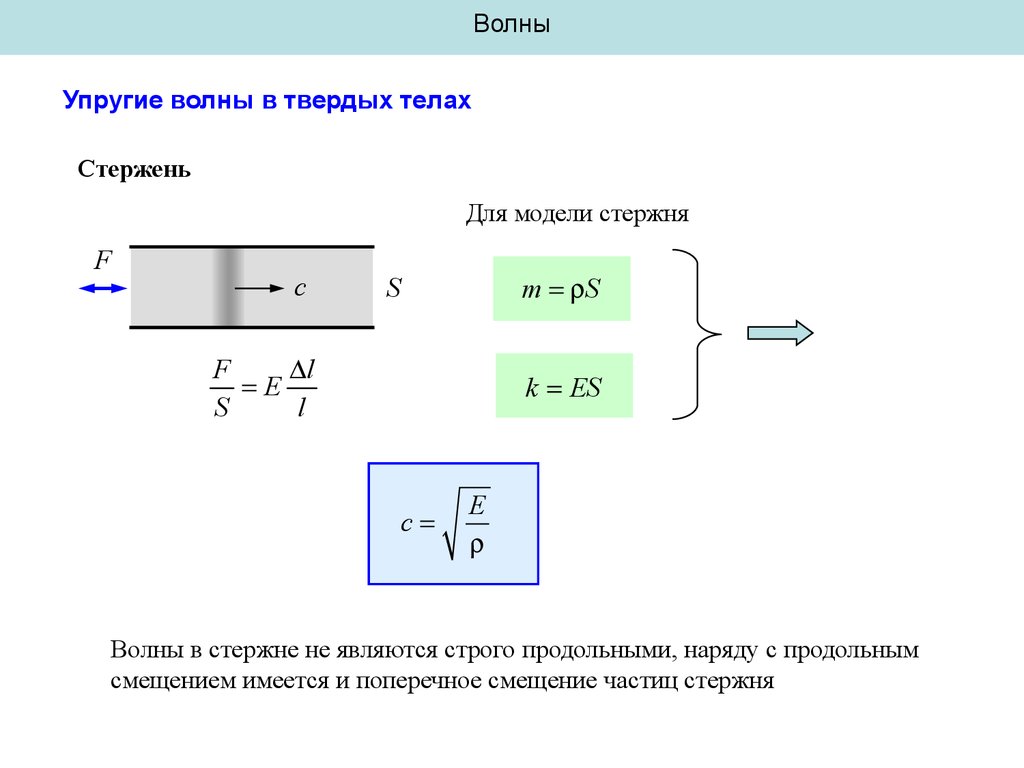
Волны
Упругие волны в твердых телах
Стержень
Для модели стержня
F
c
m S
S
F
l
E
S
l
k ES
c
E
Волны в стержне не являются строго продольными, наряду с продольным
смещением имеется и поперечное смещение частиц стержня

8.

Волны
Упругие волны в твердых телах
Неограниченная среда
а) продольная волна
Для модели стержня
F
c
S
m S
F
l
E
S
l
E
K 43 G
k E
S
– модуль одностороннего сжатия
cP
K 43 G

9.

Волны
Упругие волны в твердых телах
Неограниченная среда
а) поперечная волна
y
Fy S GS
c S
G
Для модели струны
m S
c
T GS
G
Fy T – для струны
cP c
В неограниченной среде возмущение разделится на
продольное и поперечное, причем продольное возмущение
придет в точку наблюдения быстрее поперечного

10.

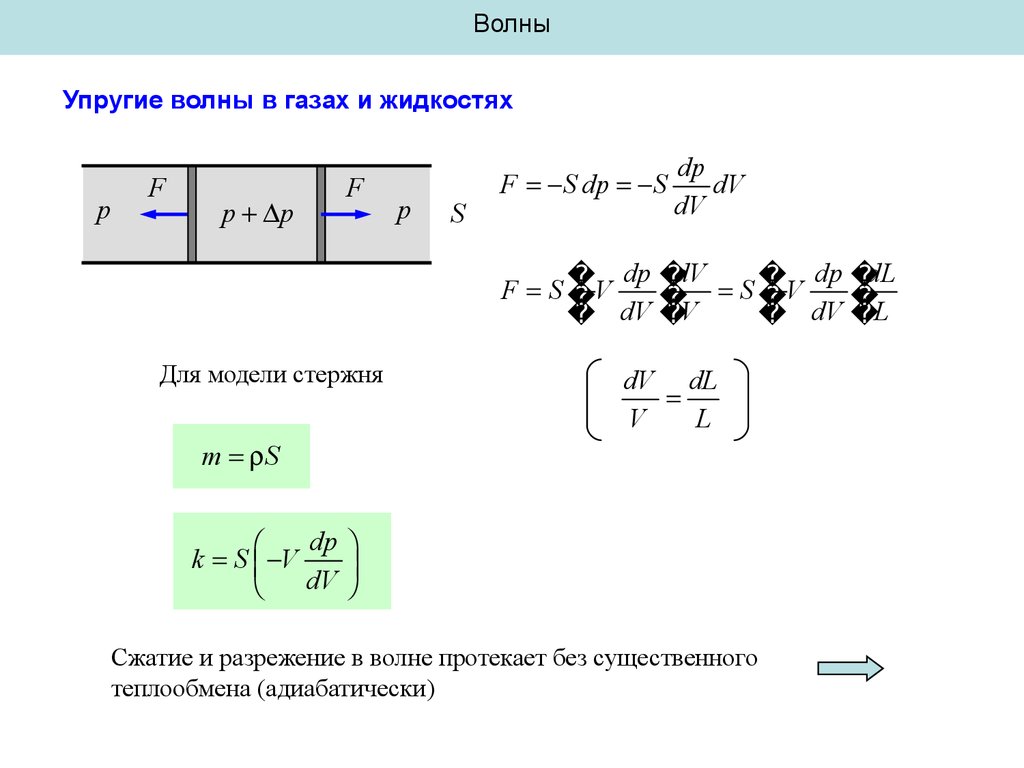
Волны
Упругие волны в газах и жидкостях
p
F
p p
F
p
S
F S dp S
dp
dV
dV
dp dV
dp
F S
V
S
V
dV V
dV
Для модели стержня
dV dL
V
L
m S
dp
k S V
dV
Сжатие и разрежение в волне протекает без существенного
теплообмена (адиабатически)
dL
L

11.

Волны
Упругие волны в газах и жидкостях
Газ
pV const
V
– уравнение адиабаты
dp
p
dV
c
p
Жидкость
dp
K S V
dV S
– адиабатический модуль объемного сжатия
c
KS

12.

Волны
Интерференция волн. Стоячие волны
1 ( x, t )
По принципу суперпозиции
2 ( x , t )
1 2
1 , 2
– когерентные волны, если их частоты равны
1 2
Интерференция:
При наложении когерентных волн возникает интерференция –
в одних точках усиление колебаний, в других – их ослабление.

13.

Волны
Интерференция волн. Стоячие волны
1 a cos( t kx )
1 2 2a sin kx cos t
2 a cos( t kx )
A( x )
x
2a sin
2
cos t
узел
– уравнение стоячей волны
пучность
A( x ) 0
– узел
| A( x ) | 2a
– пучность
( n 0, 1 , 2 K ) – узлы стоячей волны
2
x n 1
(n 0, 1 , 2 K ) – пучности стоячей волны
2 2
1)
x n
2)

14.

Волны
Интерференция волн. Стоячие волны
Струна
L
L n
n
c T m
n
c
c
n,
n 2L
Колебания
(n 1, 2, 3, ... )
2
2L
,
n
( n 1, 2, 3, ... )
– собственные частоты струны
1 c 2 L
– основная (первая) гармоника
n n 1
– n–я гармоника

15.

Волны
Энергия упругих волн. Вектор Умова
Плотность энергии волны (в стержне)
u
(t , x ) (t x c )
t
1
u
x
c
t
c
mu 2
u 2
dK
dl
dV
2
2
2
1
k 2
u 2
dU k dl 2 u dl
dV
2
x
2c
2
u 2
c2
– плотность энергии волны
k
d (K U )
dV

16.

Волны
Энергия упругих волн. Вектор Умова
Плотность потока импульса (в стержне)
jp
c
F
S
F k
x
p – импульс правой части стержня
jp
1 dp F
k
u cu
S dt S cS
u – объемная плотность импульса
j p c
– плотность потока импульса

17.

Волны
Энергия упругих волн. Вектор Умова
Плотность потока импульса (в стержне)
j
c
F
S
F k
x
E – энергия правой части стержня, A – работа силы упругости F
j
1 dE 1 dA Fu
cu 2
S dt S dt
S
u 2
dE dA,
dA
Fu
dt
– объемная плотность энергии волны
j c
– плотность потока энергии (вектор Умова)

18.

Волны
Эффект Доплера
0
источник
приемник
– частота приема (приемником)
0
1)
vист vпр 0
2)
vист и/или vпр 0
Правило знаков
vист
0 – частота излучения (источником)
vпр
0
– эффект Доплера

19.

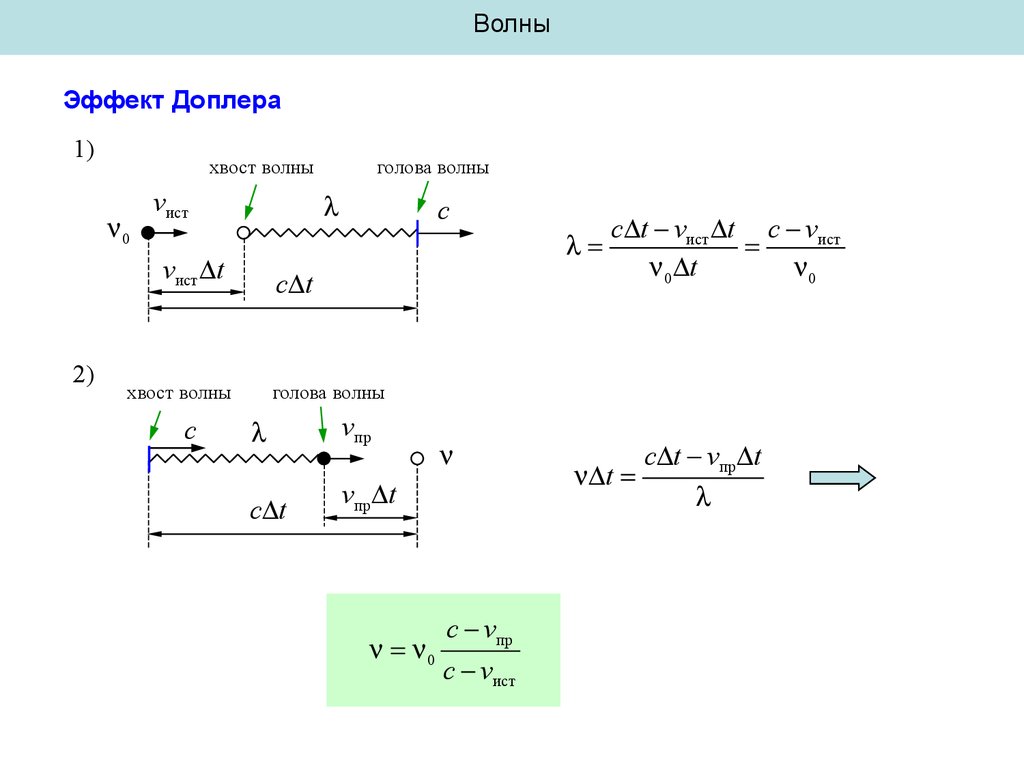
Волны
Эффект Доплера
1)
хвост волны
0
vист
c t
хвост волны
c
c
vист t
2)
голова волны
с t vист t с vист
0 t
0
голова волны
vпр
c t
vпр t
0
c vпр
c vист
t
c t vпр t