Проверка гипотез, относящихся к коэффициентам регрессии

1. Проверка гипотез, относящихся к коэффициентам регрессии

Пример 1. y –темп общей инфляции в экономике (в %),
x – темп инфляции, вызванной ростом заработной платы (в %).
yi axi b i , i 1, n
Гипотеза: общая инфляция увеличивается в той же степени, что и инфляция,
вызванная ростом заработной платы
H0 : a 1
- основная гипотеза
H1 : a 1
- альтернативная гипотеза.

2. Проверка гипотез, относящихся к коэффициентам регрессии

Пример 2. y –заработная плата,
x – число лет обучения
yi axi b i , i 1, n
Гипотеза: заработная плата не зависит от числа лет обучения
H0 : a 0
- основная гипотеза
H1 : a 0
- альтернативная гипотеза.

3.

Проверка гипотез возможна, только если выполнены 4 условия
Гаусса-Маркова, т.е. в классической нормальной линейной
модели парной регрессии
yi axi b i ,
i
N 0, 2 , i 1, n
1. Рассчитываются стандартные ошибки коэффициентов регрессии
sa
s
стандартная ошибка коэффициента а
sx n
s x2
sb
sx n
стандартная ошибка коэффициента b
Excel делает это автоматически при построении регрессии через
Сервис-Анализ данных
b

4.

Проверка гипотез возможна, только если выполнены 4 условия
Гаусса-Маркова, т.е. в классической нормальной линейной
модели парной регрессии
yi axi b i ,
N 0, 2 , i 1, n
i
2. Выдвигается основная и альтернативная гипотезы о коэффициентах
регрессии
H 0 : a a0
основная
H1 : a a0
альтернативная
Чаще всего проверяют гипотезы
H0 : a 0
H1 : a 0
- коэффициент а незначим
коэффициент а значим

5.

Проверка гипотез возможна, только если выполнены 4 условия
Гаусса-Маркова, т.е. в классической нормальной линейной
модели парной регрессии
yi axi b i ,
i
N 0, 2 , i 1, n
3. Задается уровень значимости P( H1 H0 )
Чаще всего
0.05

6.

yi axi b i ,
i
N 0, 2 ,
i 1, n
4. Рассчитывается статистика критерия
a a0
Ta
sa
b b0
Tb
sb
для гипотез
для проверки гипотезы
для проверки гипотезы
H 0 : a a0
H 0 : b b0
H0 : a 0 H0 : b 0
Excel делает это автоматически при построении регрессии через
Сервис-Анализ данных

7.

yi axi b i ,
i
N 0, 2 ,
i 1, n
5. Рассчитывается критическое значение для t статистики с помощью функции
Excel
Стьюдраспобр(альфа, n-2)

8.

yi axi b i ,
i
N 0, 2 ,
i 1, n
6. Сравнивается t-статистика с критическим значением
Если
T tkrit
, то принимается основная гипотеза
Иначе альтернативная гипотеза
H1 : a a0
H 0 : a a0

9. Проверка гипотез, относящихся к коэффициентам регрессии

Наиболее часто проверяется гипотеза
H0 : a 0
переменная y не зависит от переменной x. Уравнение регрессии не значимо.
В этом случае
a
Ta
sa

10.

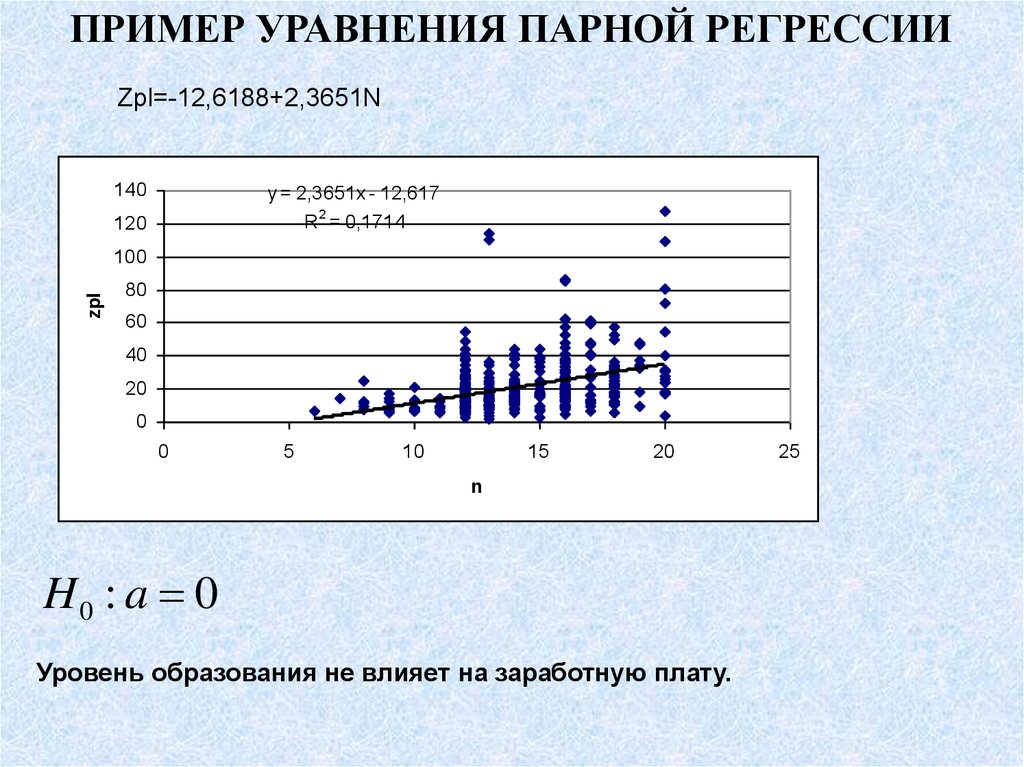
ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
Zpl=-12,6188+2,3651N
140
y = 2,3651x - 12,617
R2 = 0,1714
120
zpl
100
80
60
40
20
0
0
5
15
10
20
n
H0 : a 0
Уровень образования не влияет на заработную плату.
25

11.

ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
стандартные ошибки
t-статистики для гипотез
H0 : a 0
H0 : b 0

12.

ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
tkrit 1.96
=стьюдраспобр(0,05;540-2)
стандартные ошибки
t-статистики для гипотез
H0 : a 0
H0 : b 0

13.

ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
tkrit 1.96
=стьюдраспобр(0,05;540-2)
Так как |-4.05|>1.96, принимаем
Так как |2.37|>1.96, принимаем
H1 : b 0
H1 : a 0

14.

ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
Коэффициент
ы
Стандартная
ошибка
t-статистика
Y-пересечение
-12,6168
3,118382
-4,04596
5,97E-05
n
2,365094
0,224205
10,54881
8,96E-24
Если гипотетическое значение 0, то проверку гипотезы
и
H0 : b 0
H0 : a 0
можно выполнить проще по Р-значению
Если Р-значение меньше
иначе
P-Значение
, то принимается H1 : a 0
H0 : a 0
Р-значение - это вероятность того, что соответствующая переменная не
влияет на зависимую переменную y. При Р-значении больше 0,05 обычно
считают, что соответствующая переменная незначима и ее можно
исключить из уравнения регрессии.
Замечание. Константу из уравнения регрессии удалять нельзя, даже если
она незначима.

15.

ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
Zpl=-12,6188+2,3651N
140
y = 2,3651x - 12,617
R2 = 0,1714
120
zpl
100
80
60
40
20
0
0
5
15
10
20
n
H0 : a 2
Каждый дополнительный год обучения добавляет 2
доллара к заработной плате.
25

16.

ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
стандартные ошибки
a a0 2.365 2
Ta
1.63
sa
0.224

17.

ПРИМЕР УРАВНЕНИЯ ПАРНОЙ РЕГРЕССИИ
tkrit 1.96
=стьюдраспобр(0,05;540-2)
Так как |1.63|<1.96
принимается
H0 : a 2
a a0 2.365 2
Ta
1.63
sa
0.224

18. Пример проверки гипотезы

Пример 2. y –темп общей инфляции в экономике (в %),
x – темп инфляции, вызванной ростом заработной платы (в %).
y 0,82 x 1, 21
(0,10) (0,05)
В скобках стандартные ошибки
n=20 наблюдений
Гипотеза: общая инфляция увеличивается в той же степени, что и инфляция,
вызванная ростом заработной платы
H0 : a 1
- основная гипотеза
H1 : a 1
- альтернативная гипотеза.

19.

y 0,82 x 1, 21
(0,10) (0,05)
H0 : a 1
n=20 наблюдений
- основная гипотеза
a a0 0,82 1
Ta
1,80
sa
0,10
0, 05
=СТЬЮДРАСПОБР(0,05;20-2)
tkrit 2.1
1.8 2.1
принимаем
H0 : a 1
общая инфляция незначимо отличается
от инфляции,
вызванной
ростом заработной платы